
All Solutions
Section 4.3: Relative Motion
#### Known
The relative motion of the boat with respect to the ground is equal to:
$$
begin{align*}
boxed{vec{v}_{tx{bg}}=vec{v}_{tx{bw}}+vec{v}_{tx{wg}}}
end{align*}
$$
#### Calculation
Given: $v_{tx{bw}}=6.1 frac{tx{m}}{tx{s}}$ with a direction relative to water $theta=25^circ$, $v_{tx{wg}}=4.5 frac{tx{m}}{tx{s}}$, working with the components of $vec{v}_{tx{bw}}$ and $vec{v}_{tx{wg}}$, we have:
$$
begin{align*}
&v_{tx{bw}, x}=left(6.1 frac{tx{m}}{tx{s}}right) tx{cos}(25^circ)=5.5 frac{tx{m}}{tx{s}}\
&v_{tx{bw}, y}=left(6.1 frac{tx{m}}{tx{s}}right) tx{sin}(25^circ)=2.6 frac{tx{m}}{tx{s}}\
&v_{tx{wg}, x}=0 frac{tx{m}}{tx{s}}\
&v_{tx{wg}, y}=-4.5 frac{tx{m}}{tx{s}}\
end{align*}
$$
Therefore:
$$
begin{align*}
&v_{tx{bg}, x}=v_{tx{bw}, x}+v_{tx{wg}, x}=5.5 frac{tx{m}}{tx{s}}+0 frac{tx{m}}{tx{s}}=5.5 frac{tx{m}}{tx{s}}\
&v_{tx{bg}, y}=v_{tx{bw}, y}+v_{tx{wg}, y}=2.6 frac{tx{m}}{tx{s}}-4.5 frac{tx{m}}{tx{s}}=-1.9 frac{tx{m}}{tx{s}}
end{align*}
$$
This implies:
$$
begin{align*}
v_{tx{bg}}&=sqrt{left(v_{tx{bg}, x}right)^2+left(v_{tx{bg}, y}right)^2}\
&=sqrt{left(5.5 frac{tx{m}}{tx{s}}right)^2+left(-1.9 frac{tx{m}}{tx{s}}right)^2}\
&=5.8 frac{tx{m}}{tx{s}}
end{align*}
$$
And
$$
begin{align*}
theta=tx{tan}^{-1}left(frac{-1.9 cancel{frac{tx{m}}{tx{s}}}}{5.5 cancel{frac{tx{m}}{tx{s}}}}right)=-19^circ tx{or} 19^circ tx{downstream}
end{align*}
$$
—
#### Conclusion
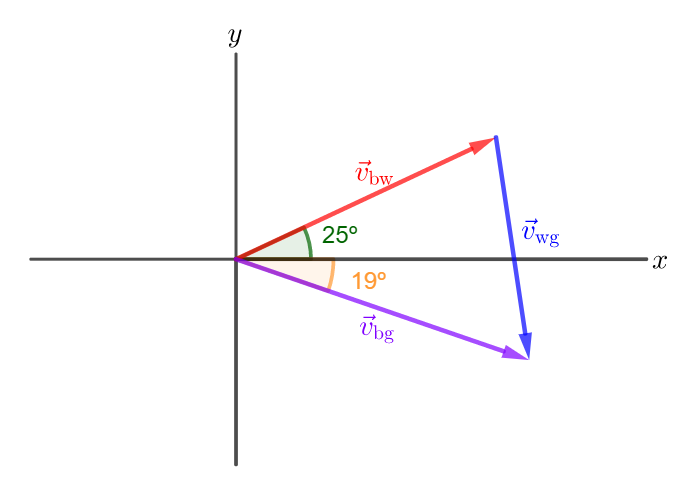
The boat is moving with a speed of $5.8 frac{tx{m}}{tx{s}}$ and $19^circ$ downstream relative to the ground.
Graphically:
#### Known
The relative motion of the airplane with respect to the ground is equal to:
$$
begin{align}
boxed{vec{v}_{tx{pg}}=vec{v}_{tx{pa}}+vec{v}_{tx{ag}}}
end{align}
$$
Where $vec{v}_{tx{pg}}$ is the velocity of the plane with respect to the ground, $vec{v}_{tx{pa}}$ is the velocity of the plane with respect to the air and $vec{v}_{tx{ag}}$ is the velocity of the air with respect to the ground (wind velocity).
#### Calculation
Givens: $v_{tx{ag}}=65 frac{tx{km}}{tx{h}}$, from east to west. $v_{tx{pa}}=340 frac{tx{km}}{tx{h}}$.
The pilot wants to travel north, so the plane will have $v_{tx{pg}, y}$ component on the $y$ axis and $v_{tx{pg}, x}=0 frac{tx{km}}{tx{h}}$ component on the $x$ axis. See Figure 1.
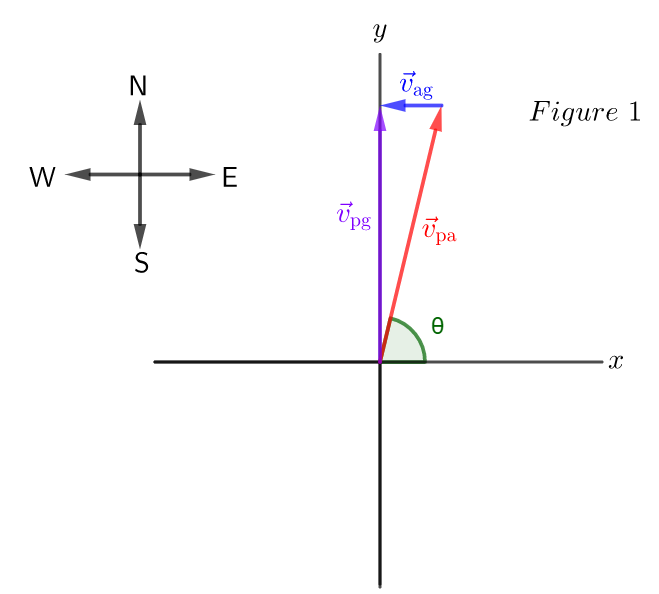
The components of the wind velocity are given by:
$$
begin{align*}
v_{tx{ag}, x}=-65 frac{tx{km}}{tx{h}}, v_{tx{ag}, y}=0 frac{tx{km}}{tx{h}}
end{align*}
$$
Choosing the positive direction from west to east and the negative from east to west.
Finally, the components of the plane’s velocity with respect to the air are:
$$
begin{align*}
v_{tx{pa}, x}=v_{tx{pa}} tx{cos}(theta)hspace{0.5cm} tx{and}hspace{0.5cm} v_{tx{pa}, y}=v_{tx{pa}} tx{sin}(theta)
end{align*}
$$
Using expression (1) in components:
$$
begin{align*}
v_{tx{pg}, y}=v_{tx{pa}, y}+v_{tx{ag}, y}
end{align*}
$$
And
$$
begin{align*}
&v_{tx{pg}, x}=v_{tx{pa}, x}+v_{tx{ag}, x}\
&v_{tx{pg}, x}=v_{tx{pa}} tx{cos}(theta)+v_{tx{ag}, x}\
&implies tx{cos}=frac{v_{tx{pg}, x}-v_{tx{ag}, x}}{v_{pa}}=frac{0 frac{tx{km}}{tx{h}}-left(-65 frac{tx{km}}{tx{h}}right)}{340 frac{tx{km}}{tx{h}}}=frac{65}{340}\
&thereforetheta=tx{cos}^{-1}left(frac{65}{340}right)=79^circ
end{align*}
$$
—
#### Conclusion
The pilot should steer the plane $79^circ$ north of east.
#### Known
The relative motion of the boat with respect to the ground is given by:
$$
begin{align*}
&vec{v}_{tx{bg}}=vec{v}_{tx{bw}}+vec{v}_{tx{wg}}\
implies &vec{v}_{tx{bg}, x}=vec{v}_{tx{bw}, x}+vec{v}_{tx{wg}, x}\
&vec{v}_{tx{bg}, y}=vec{v}_{tx{bw}, y}+vec{v}_{tx{wg}, y}
end{align*}
$$
For the boat move straight across the river (on the $x$-axis), its velocity component perpendicular to this direction must be zero (on the $y$-axis).
#### Calculation
Givens: $v_{tx{bw}(tx{before})}=6.1 frac{tx{m}}{tx{s}}$ with $theta=25^circ$ relative to water. $v_{tx{wg}}=4.5 frac{tx{m}}{tx{s}}$
Therefore:
$$
begin{align*}
&v_{tx{bg}, y}=v_{tx{bw}, y}+v_{tx{wg}, y}=0 frac{tx{m}}{tx{s}}\
implies &v_{tx{bw}, y}=-v_{tx{wg}, y}\
&v_{tx{bw}(tx{after})} tx{sin}(theta)=-vec{v}_{tx{wg}, y}\
&v_{tx{bw}(tx{after})}=frac{-v_{tx{wg}, y}}{tx{sin}(theta)}=frac{-left(-1.4 frac{tx{m}}{tx{s}}right)}{tx{sin}(25^circ)}=3.3 frac{tx{m}}{tx{s}}
end{align*}
$$
With:
$$
begin{align*}
v_{tx{bw}(tx{after})}<v_{tx{bw}(tx{before})}
end{align*}
$$
And
$$
begin{align*}
v_{tx{bw}(tx{before})}-v_{tx{bw}(tx{after})}=6.1 frac{tx{m}}{tx{s}}-3.3 frac{tx{m}}{tx{s}}=2.8 frac{tx{m}}{tx{s}}
end{align*}
$$
—
#### Conclusion
The captain should reduce the speed of the boat by $2.8 frac{tx{m}}{tx{s}}$ relative to the water.
$$
boxed{ {v}_{13} = {v}_{12} + {v}_{23} }
$$
{v}_{13} = {v}_{12} + {v}_{23}
$$
#### Known
The movement of an object depends on the reference system from which it is viewed.
If an object 1 has velocity $vec{v}_1$ with respect to an object 2, this is $vec{v}_{12}$ and object 2 has a velocity $vec{v}_2$ with respect an object 3, this is $vec{v}_{23}$, then the velocity of object 1 with respect to object 3 is $vec{v}_{13}$ and is equal to:
$$
begin{align}
boxed{vec{v}_{13}=vec{v}_{12}+vec{v}_{23}}
end{align}
$$
#### Calculation
Givens: $v_{tx{fd}}=6.2 frac{tx{m}}{tx{s}}$, moving north ($v_{tx{fd}}$ is the speed of the ferry relative to the dock). $v_{tx{pf}}=1.1 frac{tx{m}}{tx{s}}$, moving east ($v_{tx{pf}}$ is the speed of the person relative to the ferry).
From (1), we have that the velocity of the person relative to the dock is:
$$
begin{align*}
&vec{v}_{tx{pd}}=vec{v}_{tx{pf}}+vec{v}_{tx{fd}}\
implies &v_{tx{pd}, x}=v_{tx{pf}, x}+v_{tx{fd}, x}\
&v_{tx{pd}, y}=v_{tx{pf}, y}+v_{tx{fd}, y}
end{align*}
$$
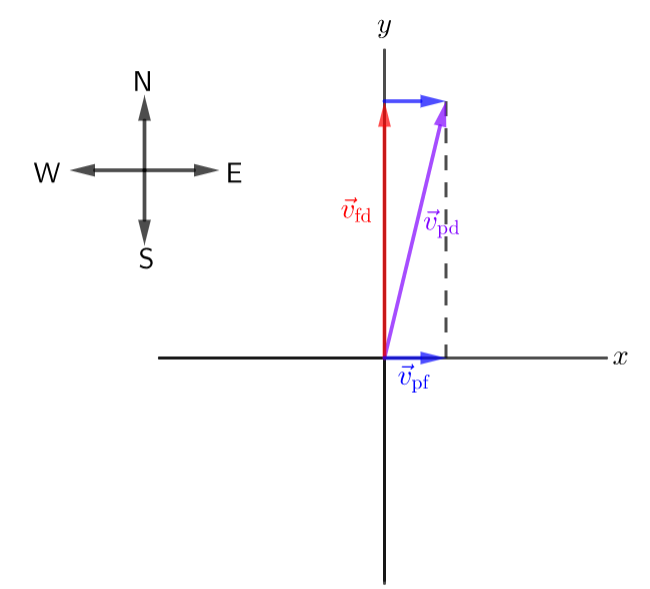
Where (see figure):
$$
begin{align*}
&v_{tx{pf}, x}=1.1 frac{tx{m}}{tx{s}}hspace{0.5cm} tx{and}hspace{0.5cm} v_{tx{pf}, y}=0 frac{tx{m}}{tx{s}}\
&v_{tx{fd}, x}=0 frac{tx{m}}{tx{s}}hspace{0.5cm} tx{and}hspace{0.5cm} v_{tx{fd}, y}=6.2 frac{tx{m}}{tx{s}}
end{align*}
$$
Therefore:
$$
begin{align*}
&v_{tx{pd}, x}=1.1 frac{tx{m}}{tx{s}}hspace{0.5cm} tx{and}hspace{0.5cm} v_{tx{pd}, y}=6.2 frac{tx{m}}{tx{s}}\
&implies vec{v}_{pd}=left(1.1 frac{tx{m}}{tx{s}}, 6.2 frac{tx{m}}{tx{s}}right)\
&implies v_{pd}=sqrt{left(1.1 frac{tx{m}}{tx{s}}right)^2+left(6.2 frac{tx{m}}{tx{s}}right)^2}=6.3 frac{tx{m}}{tx{s}}
end{align*}
$$
—
#### Conclusion
The speed of the person relative to the dock is $6.3 frac{tx{m}}{tx{s}}$.
#### Known
The movement of an object depends on the reference system from which it is viewed.
If an object 1 has velocity $vec{v}_1$ with respect to an object 2, this is $vec{v}_{12}$ and object 2 has a velocity $vec{v}_2$ with respect an object 3, this is $vec{v}_{23}$, then the velocity of object 1 with respect to object 3 is $vec{v}_{13}$ and is equal to:
$$
begin{align}
boxed{vec{v}_{13}=vec{v}_{12}+vec{v}_{23}}
end{align}
$$
#### Calculation
Givens: $v_{tx{ps}}=3.8 frac{tx{m}}{tx{s}}$, moving north ($v_{tx{ps}}$ is the speed of the person relative to the ship). $v_{tx{sw}}=12 frac{tx{m}}{tx{s}}$, moving east ($v_{tx{sw}}$ is the speed of the ship relative to the water).
From (1), we have that the velocity of the person relative to the water is:
$$
begin{align*}
&vec{v}_{tx{pw}}=vec{v}_{tx{ps}}+vec{v}_{tx{sw}}\
implies &v_{tx{pw}, x}=v_{tx{ps}, x}+v_{tx{sw}, x}\
&v_{tx{pw}, y}=v_{tx{ps}, y}+v_{tx{sw}, y}
end{align*}
$$
Where (see figure):
$$
begin{align*}
&v_{tx{pw}, x}=0 frac{tx{m}}{tx{s}}hspace{0.5cm} tx{and}hspace{0.5cm} v_{tx{pw}, y}=3.8 frac{tx{m}}{tx{s}}\
&v_{tx{sw}, x}=12 frac{tx{m}}{tx{s}}hspace{0.5cm} tx{and}hspace{0.5cm} v_{tx{sw}, y}=0 frac{tx{m}}{tx{s}}
end{align*}
$$
Therefore:
$$
begin{align*}
&v_{tx{pw}, x}=12 frac{tx{m}}{tx{s}}hspace{0.5cm} tx{and}hspace{0.5cm} v_{tx{pw}, y}=3.8 frac{tx{m}}{tx{s}}\
&implies vec{v}_{tx{pw}}=left(12 frac{tx{m}}{tx{s}}, 3.8 frac{tx{m}}{tx{s}}right)\
&thereforetheta=tx{tan}^{-1}left(frac{v_{tx{pw}, y}}{v_{tx{pw}, x}}right)=tx{tan}^{-1}left(frac{3.8 frac{tx{m}}{tx{s}}}{12 frac{tx{m}}{tx{s}}}right)=17.6^circ
end{align*}
$$
—
#### Conclusion
The person is moving with respect to the water in a direction $17.6^circ$ north of east.

