
All Solutions
Page 300: Assessment
As the textbook mentions, the angular speed of a rotating object is given by
$$
begin{align*}
omega &= dfrac{ v }{r} \
end{align*}
$$
As we know the average angular velocity $omega_{avg}$ is given by the angular displacement divided by the time interval in which the displacement occurs.
$$
begin{align*}
omega_{avg} &= dfrac{ Delta theta }{ Delta t } \
end{align*}
$$
Let us draw a line in a plane perpendicular to the axis of rotation that connects the axis with the projection of the position of a particle in that plane. By doing this method several times for different points on the object within the same time interval, then you get the same angular displacement. So, All of the objects have the same angular speed. But the linear speed is not the same since points farther from the axis sweep larger arcs than those that are closer for the same cases.
But the linear speed is not the same since points farther from the axis sweep larger arcs than those that are closer for the same cases.
As the textbook mentions, the tangential speed of a rotating object is given by
$$
begin{align*}
v &= r ~ omega \
end{align*}
$$
You should stand on the closest point to the Earth’s axis of rotation to get the smallest possible linear speed that you minimizer the distance $r$ between Earth’s and you. Also, To get the greater possible linear speed, you should stand on the farthest point from the axis of rotation of Earth which lies on the equator.
You should stand on the farthest point from the axis of rotation of Earth which lies on the equator.
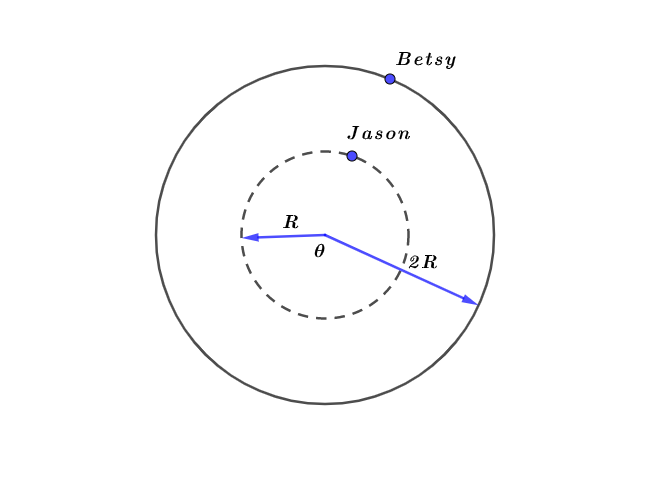
From the graph data, we see that at any time interval $Delta t$, the angular displacement (position) $Delta theta$ of Jason is the same as that of Betsy.
As we know the average angular velocity $omega_{avg}$ is given by the angular displacement divided by the time interval in which the displacement occurs.
$$
begin{align*}
omega_{avg} &= dfrac{ Delta theta }{ Delta t } \
end{align*}
$$
So, the angular speed of Jason is the same as that of Betsy.
As we see from part (a), the best explanation is (C) The angular speeds are the same because it takes the
the same amount of time for Jason and Betsy to complete a revolution.
(b) C. The angular speeds are the same because it takes the same amount of time for Jason and Betsy to complete a revolution.
So,$quad 20^circ=Big(dfrac{2pi}{360^circ}times 20^circBig)rad=big(dfrac{pi}{9}big)radapprox(0.35)rad$
$quad 35^circ=Big(dfrac{2pi}{360^circ}times 35^circBig)rad=big(dfrac{7pi}{36}big)radapprox(0.61)rad$
$quad 80^circ=Big(dfrac{2pi}{360^circ}times 80^circBig)rad=big(dfrac{4pi}{9}big)radapprox(1.40)rad$
$$
quad 270^circ=Big(dfrac{2pi}{360^circ}times 270^circBig)rad=big(dfrac{3pi}{2}big)radapprox(4.71)rad
$$
begin{align*}
20^{circ} &= 0.35 mathrm{~rad} \
35^{circ} &= 0.61 mathrm{~rad} \
80^{circ} &= 1.4 mathrm{~rad} \
270^{circ} &= 4.71 mathrm{~rad} \
end{align*}
$$
So,$quad(dfrac{pi}{3})rad=Big(dfrac{360^circ}{2pi}timesdfrac{pi}{3}Big)=60^circ$
$(0.40pi)rad=Big(dfrac{360^circ}{2pi}times0.40piBig)=72^circ$
$(1.7pi)rad=Big(dfrac{360^circ}{2pi}times1.7piBig)=306^circ$
$$
(6pi)rad=Big(dfrac{360^circ}{2pi}times6piBig)=1080^circ
$$
begin{align*}
dfrac{pi}{3} mathrm{rad} &= 60^{circ} \
0.4 ~ pi mathrm{rad} &= 72^{circ} \
1.7 pi mathrm{rad} &= 306^{circ} \
6 pi mathrm{rad} &= 1080^{circ} = 360^{circ} \
end{align*}
$$
Since the second hand on the clock is the minute hand. So, the period of the second hand for one revolution is $1 mathrm{~min}$. Therefore the angular velocity in terms of $mathrm{~rev/hr}$ equals to
$$
begin{align*}
omega &= dfrac{ 1 mathrm{~rev} }{ 1 mathrm{~min} } \
&= dfrac{ 1 mathrm{~rev} }{ 1 mathrm{~min} } times dfrac{ 60 mathrm{~min} }{ 1 mathrm{~hr} } \
&= 60 mathrm{~rev/hr}
end{align*}
$$
So, the angular velocity in terms of $mathrm{~rev/hr}$ is $60 mathrm{~rev/hr}$.
Since the second hand on the clock is the minute hand. So, the period of the second hand for one revolution is $1 mathrm{~min}$. Therefore the angular velocity in terms of $mathrm{~deg/min}$ equals to
$$
begin{align*}
omega &= dfrac{ 1 mathrm{~rev} }{ 1 mathrm{~min} } \
&= dfrac{ 1 mathrm{~rev} }{ 1 mathrm{~min} } times 360 mathrm{~deg} \
&= 360 mathrm{~deg/min}
end{align*}
$$
So, the angular velocity in terms of $mathrm{~deg/min}$ is $360 mathrm{~deg/min}$.
Since the second hand on the clock is the minute hand. So, the period of the second hand for one revolution is $1 mathrm{~min}$. Therefore the angular velocity in terms of $mathrm{~rad/s}$ equals to
$$
begin{align*}
omega &= dfrac{ 1 mathrm{~rev} }{ 1 mathrm{~min} } \
&= dfrac{ 360 mathrm{~deg} }{ 1 mathrm{~min} } times dfrac{ 2 pi mathrm{~rad} }{ 360 mathrm{~deg} } times dfrac{ 1 mathrm{~min} }{ 60 mathrm{~s} } \
&= dfrac{pi }{ 30 } mathrm{~rad/s}
end{align*}
$$
So, the angular velocity in terms of $mathrm{~rad/s}$ is $dfrac{pi }{ 30 } mathrm{~rad/s}$.
(b) The angular velocity in terms of $mathrm{~deg/min}$ is $360 mathrm{~deg/min}$.
(c) The angular velocity in terms of $mathrm{~rad/s}$ is $dfrac{pi }{ 30 } mathrm{~rad/s}$.
The angular speed of the carousel is $omega = dfrac{1}{45} mathrm{~rev}{s}$.
$textbf{Required: }$
(a) Finding the linear speed of the outer horse on the carousel, if the radius of the circular path is $2.75 mathrm{~m}$.
(b) Finding the linear speed of the inner horse on the carousel, if the radius of the circular path is $1.75 mathrm{~m}$.
Solve for the linear speed of the outer horse:
As the textbook mentions, the angular speed is given by
$$
begin{align*}
omega &= dfrac{ v}{r} \
end{align*}
$$
As the textbook mentions, the tangential speed of a rotating object is given by
$$
begin{align*}
v &= r ~ omega \
&= 2.75 mathrm{~m} times dfrac{1}{ 45 } times 2 pi mathrm{~rad/s} \
&= 0.384 mathrm{~m/s}
end{align*}
$$
So, the linear speed of the outer horse on the carousel is $0.384 mathrm{~m/s}$.
Solve for the linear speed of the inner horse:
As the textbook mentions, the angular speed is given by
$$
begin{align*}
omega &= dfrac{ v}{r} \
end{align*}
$$
As the textbook mentions, the tangential speed of a rotating object is given by
$$
begin{align*}
v &= r ~ omega \
&= 1.75 mathrm{~m} times dfrac{1}{ 45 } times 2 pi mathrm{~rad/s} \
&= 0.244 mathrm{~m/s}
end{align*}
$$
So, the linear speed of the inner horse on the carousel is $0.244 mathrm{~m/s}$.
(b) The linear speed of the inner horse on the carousel is $0.244 mathrm{~m/s}$.
So, angular speed , $qquad omega=dfrac{1text{ rev}}{33ms}=dfrac{(2pi)rad}{(33times10^{-3})s}approxboxed{(190)rad/s}$
The angular speed of the reel is $omega = 3 mathrm{~rev/s}$.
$textbf{Required: }$
(a) Finding the linear speed, if the reel’s radius is $r = 3.7 mathrm{~cm}$.
(b) Finding the linear speed, if the reel’s radius is $r = 2 times 3.7 mathrm{~cm}$.
As the textbook mentions, the angular speed is given by
$$
begin{align*}
omega &= dfrac{ v}{r} \
end{align*}
$$
As the textbook mentions, the tangential speed of a rotating object is given by
$$
begin{align*}
v &= r ~ omega \
&= 3.7 times 10^{-2} mathrm{~m} times 3 times 2 pi mathrm{~rad/s} \
&= 0.697 mathrm{~m/s}
end{align*}
$$
So, the linear speed of the fishing line is $0.697 mathrm{~m/s}$.
As the textbook mentions, the angular speed is given by
$$
begin{align*}
omega &= dfrac{ v}{r} \
end{align*}
$$
As the textbook mentions, the tangential speed of a rotating object is given by
$$
begin{align*}
v &= r ~ omega \
&= 2 times 3.7 times 10^{-2} mathrm{~m} times 3 times 2 pi mathrm{~rad/s} \
&= 1.395 mathrm{~m/s}
end{align*}
$$
So, the linear speed of the fishing line is $1.395 mathrm{~m/s}$.
(b) The linear speed of the fishing line is $1.395 mathrm{~m/s}$.
b) Clock needle on a ticking clock has rotational kinetic energy and zero linear kinetic energy.
c) Car wheel has both translational and rotational kinetic energy while the car is moving.
Solve for both cans have the same diameter and weight:
Since the two cans have the same initial speed. So, if the Chucky stew rolls much farther than the broth’s can, then the moment of inertia of the chunky stew can be lower than the moment of inertia of the broth can. Since the beef parts being closer to the axis of rotation. Therefore, the chunky stew can have been accelerated faster.
Since the mass of the minute hand is equal to the mass of the hour hand.
As the textbook mentions that the moment of inertia of a disk is given by
$$
begin{align*}
I &= dfrac{1}{2} ~ m ~ r^{2} \
end{align*}
$$
Since the minute hand is long, thin, and uniform and the hour hand is short, thick, and uniform, then the moment of inertia of the minute hand would be greater than that of the hour hand. Because the center of mass of the minute hand lies farther away from the axis of rotation as compared to the hour hand.
As we mention in part (a), the center of mass of the minute hand lies farther away from the axis of rotation as compared to the hour hand. So, the correct answer is (B) Having mass farther from the axis of rotation results
in a greater moment of inertia.
(b) B. Having mass farther from the axis of rotation results in a greater moment of inertia.
The angular speed of the large wheel is $omega = 0.373 mathrm{~rev/s}$. The radius of the large wheel is $r = 0.26 mathrm{~m}$.
$textbf{Required: }$
Finding the linear speed of the child.
As the textbook mentions, the angular speed is given by
$$
begin{align*}
omega &= dfrac{ v}{r} \
end{align*}
$$
As the textbook mentions, the tangential speed of a rotating object is given by
$$
begin{align*}
v &= r ~ omega \
&= 0.26 mathrm{~m} times 0.373 times 2 pi mathrm{~rad/s} \
&= 0.609 mathrm{~m/s}
end{align*}
$$
So, the linear speed of the child is $0.609 mathrm{~m/s}$.
The angular speed of the fan is $omega = 13 mathrm{~rad/s}$. The rotational kinetic energy of the fan is $K.E_{rot} = 4.6 mathrm{~J}$.
$textbf{Required: }$
Finding the moment of inertia of the fan.
As the textbook mentions that the rotational kinetic energy is given by
$$
begin{align*}
K.E_{rot} &= dfrac{1}{2} ~ I ~ omega^{2} \
end{align*}
$$
Rearrange and solve for the moment of inertia of the fan:
$$
begin{align*}
I &= dfrac{2 K.E_{rot} }{ omega^{2} } \
&= dfrac{ 2 times 4.6 mathrm{~J} }{ left( 13 mathrm{~rad/s} right)^{2} } \
&= boxed{0.0544 mathrm{~kg cdot m^{2}}}
end{align*}
$$
So, the moment of inertia of the fan is $0.0544 mathrm{~kg cdot m^{2}}$.
The mass of the rotating disk is $m = 0.51 mathrm{~kg}$. The disk’s radius is $r = 0.22 mathrm{~m}$. The angular speed of the disk is $omega = 0.4 mathrm{~rad/s}$.
$textbf{Required: }$
Finding the angular momentum of the rotating disk.
As the textbook mentions that the moment of inertia of the hollow sphere is given by
$$
begin{align*}
I &= dfrac{1}{2} ~ m ~ r^{2} \
end{align*}
$$
As the textbook mentions that the angular momentum is given by the product of an object’s momentum of inertia and its angular speed
$$
begin{align*}
L &= I ~ omega \
&= dfrac{1}{2} ~ m ~ r^{2} ~ omega \
&= dfrac{1}{2} times 0.51 mathrm{~kg} times left( 0.22 mathrm{~m} right)^{2} times 0.4 mathrm{~rad/s} \
&= 4.937 times 10^{-3} mathrm{~kg cdot m^{2}/s}
end{align*}
$$
So, the angular momentum of the disk is $4.937 times 10^{-3} mathrm{~kg cdot m^{2}/s}$.
The linear speed at the top of the wheels is $v_{t} = 43 mathrm{~m/s}$.
$textbf{Required: }$
(a) Finding the linear speed of the axles of the wheels.
(b) Finding the linear speed of the bottoms of the wheels.
In order to evaluate the linear speed of the axels of the wheels, we use the following relation:
$$
begin{align*}
v_{a} &= dfrac{ 1}{2} ~ v_{t} \
&= dfrac{1}{2} times 43 mathrm{~m/s} \
&= boxed{21.5 mathrm{~m/s}}
end{align*}
$$
So, the linear speed of the axels of the wheels is $21.5 mathrm{~m/s}$.
From part (a), the linear speed of the axels is equal to $21.5 mathrm{~m/s}$ and the linear speed at the top of the wheels is $v_{t} = 43 mathrm{~m/s}$. As we know the linear speed of the bottom of the wheels equals zero. Because the bottom point of the wheel that contacts the ground that makes friction force with the ground.
(b) The linear speed of the bottom of the wheels equals zero.
The circumference of the ball is $c = 0.7 mathrm{~m}$. The distance that the ball rolls is $Delta x = 14 mathrm{~m}$. The time interval that the balls takes is $Delta t = 3.35 mathrm{~s}$.
$textbf{Required: }$
Finding the angular speed of the ball during the time interval.
Solve for the linear speed of the ball:
In order to evaluate the circumference of the ball, we use the following relation:
$$
begin{align*}
c &= 2 ~ pi ~ r \
end{align*}
$$
Rearrange and solve for the radius of the ball:
$$
begin{align*}
r &= dfrac{ c }{ 2 pi } \
&= dfrac{ 0.7 mathrm{~m} }{ 2 pi } \
&= 0.111 mathrm{~m}
end{align*}
$$
As the textbook mentions, the angular speed is given by
$$
begin{align*}
omega &= dfrac{ v}{r} \
&= dfrac{ dfrac{ Delta x }{ Delta t } }{ r } \
&= dfrac{ Delta x }{ Delta t ~ r } \
&= dfrac{14 mathrm{~m} }{ 0.111 mathrm{~m} cdot 3.35 mathrm{~s} } \
&= boxed{37.65 mathrm{~rev/s} }
end{align*}
$$
So, the angular speed of the ball during the time interval is $37.65 mathrm{~rev/s}$.
Linear speed of ball ,$quad v_1=(2.8)m/s$
Diameter of ball ,$quad D=(0.22)m$
Radius of ball ,$quad R=dfrac{D}{2}=(0.11)m$
Now ,$quad v_1=Romegaqquad,$
Angular speed of the ball ,$qquadomega_1=dfrac{v_1}{R}=Big(dfrac{2.8}{0.11}Big)rad/s$
$Rightarrowquadboxed{omega_1=(25.5)rad/s}$
$b)quad$Given :
Angular speed of ball on reaching the top ,$quad omega_2=(1.2)rad/s$
So , linear speed,$quad v_2=Romega_2=big((0.11)(1.2)big)m/s$
$$
Rightarrowquadboxed{v_2=(0.132)m/s}
$$
(b) The linear speed is $v_{2} = 0.132 mathrm{~m/s}$.
Solve for the first force at $F_{1}$:
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau_{1} &= r_{1} ~ F_{1} \
end{align*}
$$
Solve for the second force at $F_{2}$:
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau_{2} &= r_{2} ~ F_{2} \
end{align*}
$$
Since the two forces produce the same torque $tau_{1} = tau_{2}$. Then we get
$$
begin{align*}
tau_{1} &= tau_{2} \
r_{1} ~ F_{1} &= r_{2} ~ F_{2} \
end{align*}
$$
Rearrange and solve for the second force:
$$
begin{align*}
F_{2} &= dfrac{ r_{1} }{ r_{2} } ~ F_{1} \
end{align*}
$$
So, the two forces are equal in magnitude, if and only if, the two distances (arms) are the same.
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau &= r ~ F \
end{align*}
$$
As we see the magnitude of the torque depends on two factors (the force and the moment arm). So, if a larger force has a moment arm much less than the moment arm of the smaller force, then the larger force produces torque much less than the torque produced by the smaller force. Which we can consider the previous example as a counterexample. So, the answer is “No, a larger force doesn’t always produce more torque than a smaller force.”
Solve for the force at $A$:
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau_{A} &= r_{A} ~ F_{A} \
&= 10 mathrm{~m} cdot 5 mathrm{~N} \
&= boxed{50 mathrm{~N cdot m}}
end{align*}
$$
Solve for the force at $B$:
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau_{B} &= r_{B} ~ F_{B} \
&= 1.5 mathrm{~m} cdot 10 mathrm{~N} \
&= boxed{15 mathrm{~N cdot m}}
end{align*}
$$
Solve for the force at $C$:
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau_{C} &=r_{C} ~ F_{C} \
&= 0.5 mathrm{~m} cdot 1 mathrm{~N} \
&= boxed{0.5 mathrm{~N cdot m}}
end{align*}
$$
Solve for the force at $D$:
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau_{D} &= r_{D} ~ F_{D} \
&= 2.5 mathrm{~m} cdot 20 mathrm{~N} \
&= boxed{50 mathrm{~N cdot m}}
end{align*}
$$
So, the ranking in order to increase the torque is $A = D > B > C$.
The wrench’s radius is $r = 0.22 mathrm{~m}$. The force that exerted on the end of the wrench by the mechanic is $F = 58 mathrm{~N}$.
$textbf{Required: }$
Finding the producing torque by the force.
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau &= r ~ F \
&=r ~ F ~ sin left( theta right) \
&= 0.22 mathrm{~m} times 58 mathrm{~N} times sin left( 90^{circ} right) \
&= 12.76 mathrm{~N cdot m}
end{align*}
$$
So, the producing torque by the force is $12.76 mathrm{~N cdot m}$.
$$
tau=rF,
$$
where $r$ is the length of the person’s arm and $F$ the force that acts on the arm.
The force of the crab trap:
$$
F=mg=3.6cdot9.81=textbf{35.32 N}
$$
Substitute the force in the torque equation to get the torque exerted on the arm:
$$
boxed{tau=0.7cdot 35.32=24.72:Nm}
$$
tau=24.72:Nm
$$
The radius of the wheel is $r = 0.35 mathrm{~m}$. The mass of the wheel is $m = 0.75 mathrm{~kg}$. The torque that applied to the wheel is $tau = 0.97 mathrm{~N cdot m}$.
$textbf{Required: }$
Finding the angular acceleration of the wheel.
In order to evaluate the torquel, we use the following relation:
$$
begin{align*}
tau &= alpha ~ I \
end{align*}
$$
In order to evaluate the moment of inertia of the wheel as hoop, we use the following relation:
$$
begin{align*}
I &= m ~ r^{2} \
end{align*}
$$
Substituting from the previous calculation, then we get
$$
begin{align*}
alpha &= dfrac{ tau }{ I } \
&= dfrac{ tau }{ m ~ r^{2} } \
&= dfrac{ 0.97 mathrm{~N cdot m} }{ 0.75 mathrm{~kg} times left( 0.35 mathrm{~m} right)^{2} } \
&= 10.558 mathrm{~rad/s^{2}}
end{align*}
$$
So, the angular acceleration of the wheel is $10.558 mathrm{~rad/s^{2}}$.
The weight of the baseball is $W_{b} = 1.42 mathrm{~N}$. The distance between the ball and the elbow is $L = 34 mathrm{~cm}$ . The distance between the biceps and the elbow is $r_{2} = 2.75 mathrm{~cm}$.The force exerted by the biceps on the forearm is $F_{2} = 12.6 mathrm{~N}$ upward. The mass of the forearm is $M = 1.2 mathrm{~kg}$.
$textbf{Required: }$
(a) Finding the net torque that acting on the forearm and the hand.
(b) Finding the direction in which the forearm and the hand rotate, if the torque is non-zero.
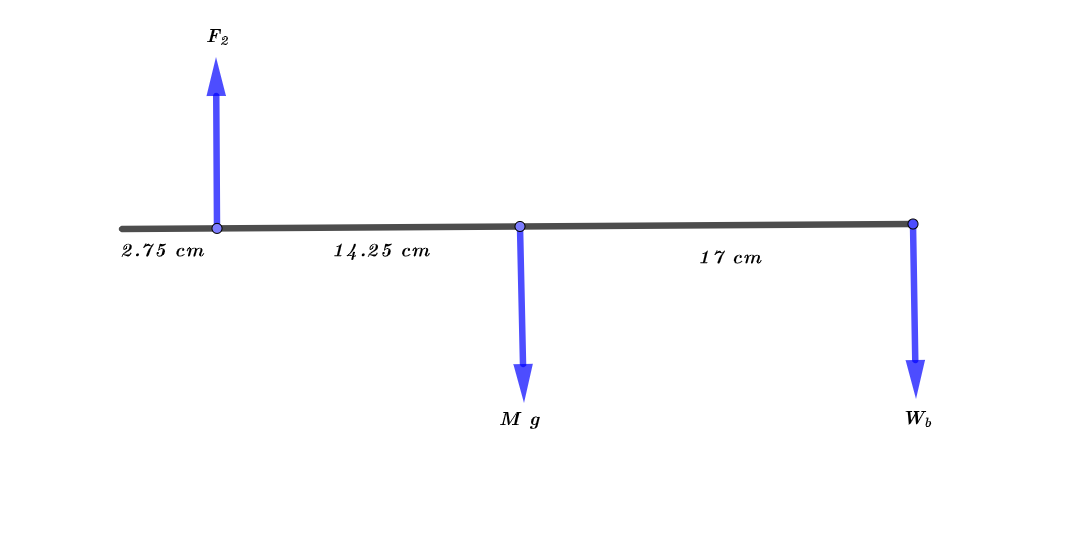
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau &= r ~ F \
end{align*}
$$
In order to evaluate the net torque that acting on the forearm and the hand, we use the superposition principle:
$$
begin{align*}
tau_{t} &= r_{1} ~ F_{1} + r_{2} ~ F_{2} + r_{3} ~ F_{3} \
&= r_{1} ~ M ~ g + r_{2} ~ F_{2} + r_{3} ~ W_{b} \
&= left( – 17 times 10^{-2} mathrm{~m} times 1.2 mathrm{~kg} times 9.8 mathrm{~m/s^{2}} right) + left( 2.75 times 10^{-2} mathrm{~m} times 12.6 mathrm{~N} right) + left( – 34 times 10^{-2} mathrm{~m} times 1.42 mathrm{~N} right) \
&= – 2.1355 mathrm{~N cdot m}
end{align*}
$$
So, the net torque that acting on the forearm and the hand is $2.1355 mathrm{~N cdot m}$ downward.
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau &= r ~ F \
end{align*}
$$
In order to evaluate the net torque that acting on the forearm and the hand, we use the superposition principle:
$$
begin{align*}
tau_{t} &= r_{1} ~ F_{1} + r_{2} ~ F_{2} + r_{3} ~ F_{3} \
&= r_{1} ~ M ~ g + r_{2} ~ F_{2} + r_{3} ~ W_{b} \
&= left( – 17 times 10^{-2} mathrm{~m} times 1.2 mathrm{~kg} times 9.8 mathrm{~m/s^{2}} right) + left( 2.75 times 10^{-2} mathrm{~m} times 12.6 mathrm{~N} right) + left( – 34 times 10^{-2} mathrm{~m} times 1.42 mathrm{~N} right) \
&= – 2.1355 mathrm{~N cdot m}
end{align*}
$$
So, the net torque that acting on the forearm and the hand is $2.1355 mathrm{~N cdot m}$ downward. So, the direction of the net torque that acting on the forearm and the hand is clockwise direction.
(b) The direction of the net torque that acting on the forearm and the hand is clockwise direction.
The mass of the child is $m_{c} = 16 mathrm{~kg}$. The distance between the pivot point and the child is $r_{1} = 1.5 mathrm{~m}$ . The force that the adult person exerts on the teeter-totter $F_{2} = 95 mathrm{~N}$.
$textbf{Required: }$
(a) Finding the direction of the teeter-totter rotation, if the distance between the adult person and the pivot point is $r_{2} = 3 mathrm{~m}$.
(b) Finding the direction of the teeter-totter rotation, if the distance between the adult person and the pivot point is $r_{2} = 2.5 mathrm{~m}$.
(c) Finding the direction of the teeter-totter rotation, if the distance between the adult person and the pivot point is $r_{2} = 23 mathrm{~m}$.
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau &= r ~ F \
end{align*}
$$
In order to evaluate the net torque that acting on the forearm and the hand, we use the superposition principle:
$$
begin{align*}
tau_{t} &= r_{1} ~ F_{1} + r_{2} ~ F_{2} \
&= r_{1} ~ W_{c} + r_{2} ~ F_{2} \
&= r_{1} ~ m_{c} ~ g + r_{2} ~ F_{2} \
&= left( – 1.5 mathrm{~m} times 16 mathrm{~kg} times 9.8 mathrm{~m/s^{2}} right) + left( 3 mathrm{~m} times 95 mathrm{~N} right) \
&=49.8 mathrm{~N cdot m}
end{align*}
$$
So, the net torque that acting on the forearm and the hand is $49.8 mathrm{~N cdot m}$. So, the teeter-totter rotates anticlockwise.
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau &= r ~ F \
end{align*}
$$
In order to evaluate the net torque that acting on the forearm and the hand, we use the superposition principle:
$$
begin{align*}
tau_{t} &= r_{1} ~ F_{1} + r_{2} ~ F_{2} \
&= r_{1} ~ W_{c} + r_{2} ~ F_{2} \
&= r_{1} ~ m_{c} ~ g + r_{2} ~ F_{2} \
&= left( – 1.5 mathrm{~m} times 16 mathrm{~kg} times 9.8 mathrm{~m/s^{2}} right) + left( 2.5 mathrm{~m} times 95 mathrm{~N} right) \
&= 2.3 mathrm{~N cdot m}
end{align*}
$$
So, the net torque that acting on the forearm and the hand is $2.3 mathrm{~N cdot m}$. So, the teeter-totter rotates anticlockwise.
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau &= r ~ F \
end{align*}
$$
In order to evaluate the net torque that acting on the forearm and the hand, we use the superposition principle:
$$
begin{align*}
tau_{t} &= r_{1} ~ F_{1} + r_{2} ~ F_{2} \
&= r_{1} ~ W_{c} + r_{2} ~ F_{2} \
&= r_{1} ~ m_{c} ~ g + r_{2} ~ F_{2} \
&= left( – 1.5 mathrm{~m} times 16 mathrm{~kg} times 9.8 mathrm{~m/s^{2}} right) + left( 2 mathrm{~m} times 95 mathrm{~N} right) \
&= – 45.2 mathrm{~N cdot m}
end{align*}
$$
So, the net torque that acting on the forearm and the hand is $- 45.2 mathrm{~N cdot m}$. So, the teeter-totter rotates clockwise.
(b) The teeter-totter rotates anticlockwise.
(c) The teeter-totter rotates clockwise.
The mass of the child is $m_{c} = 25 mathrm{~kg}$. The distance between the pivot point and the child is $r_{1} = 2 mathrm{~m}$ . The mass that placed on the other side is $m$. The distance between the mass $m$ and the pivot point is $d$. The net torque at the center is $0 mathrm{~N cdot m}$.
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau &= r ~ F \
end{align*}
$$
In order to evaluate the net torque that acting on the forearm and the hand, we use the superposition principle:
$$
begin{align*}
tau_{t} &= r_{1} ~ F_{1} + r_{2} ~ F_{2} \
&= r_{1} ~ W_{c} + r_{2} ~ F_{2} \
&= r_{1} ~ m_{c} ~ g + r_{2} ~ F_{2} \
&= left( – 2 mathrm{~m} times 25 mathrm{~kg} times 9.8 mathrm{~m/s^{2}} right) + left( d times m ~ times 9.8 mathrm{~m/s^{2}} right) \
&=0 mathrm{~N cdot m} \
d ~ m &= 50 mathrm{~kg cdot m}
end{align*}
$$
Solve for object $A$:
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau &= r ~ F \
&= 2 mathrm{~m} times 10 mathrm{~kg} \
&= 20 mathrm{~kg cdot m}
end{align*}
$$
So, it doesn’t balance the teeter-totter.
Solve for object $B$:
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau &= r ~ F \
&= 1 mathrm{~m} times 50 mathrm{~kg} \
&= 50 mathrm{~kg cdot m}
end{align*}
$$
So, it balances the teeter-totter.
Solve for object $C$:
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau &= r ~ F \
&= 1.5 mathrm{~m} times 40 mathrm{~kg} \
&= 60 mathrm{~kg cdot m}
end{align*}
$$
So, it doesn’t balance the teeter-totter.
Solve for object $D$:
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau &= r ~ F \
&= 2.5 mathrm{~m} times 20 mathrm{~kg} \
&= 50 mathrm{~kg cdot m}
end{align*}
$$
So, it balances the teeter-totter.
So, the combinations of mass and distance $B$ and $D$ balances the teeter-totter.
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau &= r ~ F \
&=r ~ F ~ sin left( theta right) \
end{align*}
$$
Since the center of mass of the first trophy is higher than that of the second trophy, then the force required to tip the first trophy is less than the force required to tip the second trophy. Therefore, when we push it a bit, the gravity will produce greater torque than in the case of the second trophy and it will help us tip it easier.
The left scale reading is $F_{1} = 290 mathrm{~N}$. The right scale reading is $F_{2} = 122 mathrm{~N}$. The distance between the two scales is $r = 2.5 mathrm{~m}$.
$textbf{Required: }$
(a) Finding the mass of the student.
(b) Finding the distance between the student’s head and the center of mass.
According to Newton’s second law in the vertical direction:
$$
begin{align*}
sum F_{Y} &= F_{1} + F_{2} – W \
&= m ~ a
end{align*}
$$
Since the plank is static, the acceleration equals zero. Substituting in the previous equation, then we get
$$
begin{align*}
sum F_{Y} &= F_{1} + F_{2} – m ~ g \
&= m ~ a \
&= 0 \
end{align*}
$$
Rearrange and solve for the mass of the student:
$$
begin{align*}
m &= dfrac{ F_{1} + F_{2} }{ g } \
&= dfrac{ 290 mathrm{~N} + 122 mathrm{~N} }{ 9.8 mathrm{~m/s^{2}} } \
&= 42.041 mathrm{~kg}
end{align*}
$$
So, the mass of the student is $42.041 mathrm{~kg}$.
As the textbook mentions, the balance point corresponds to zero net torque assigns that
$$
begin{align*}
tau &= F_{1} r_{1} – m_{2} ~ g ~ r_{2} \
&= 0 \
F_{1} ~ r_{1} &= m_{2} ~ g ~ r_{2} \
end{align*}
$$
Rearrange and solve for the distance between the center of mass and the student’s head:
$$
begin{align*}
r_{2} &= dfrac{ F_{1} ~ r_{1} }{ m_{2} ~ g} \
&= dfrac{ F_{1} ~ r_{1} }{ m ~ g} \
&= dfrac{ 122 mathrm{~N} cdot 2.5 mathrm{~m} }{ 42.041 mathrm{~kg} cdot 9.8 mathrm{~m/s^{2}} } \
&= boxed{0.74 mathrm{~m}}
end{align*}
$$
So, the center of mass and the student’s head is $0.74 mathrm{~m}$.
(b) The center of mass and the student’s head is $0.74 mathrm{~m}$.
The feet length is $l = 3.2 mathrm{~m}$. The relation between the two forces is $F_{2} = dfrac{1}{2} F_{1}$.
$textbf{Required: }$
Finding the distance between the rear feet and the triceratops’s center of mass.
According to Newton’s second law:
$$
begin{align*}
sum F &= F_{1} + F_{2} – W \
&= m ~ a \
&= 0
end{align*}
$$
Rearrange and solve for the weight:
$$
begin{align*}
W &= F_{1} + F_{2} \
&= 3 ~ F_{2}
end{align*}
$$
As the textbook mentions, the balance point corresponds to zero net torque assigns that
$$
begin{align*}
tau &= F_{2} ~ l – W ~ r_{2} \
&= 0 \
F_{2} ~ l &= W ~ r_{2} \
end{align*}
$$
Rearrange and solve for the distance between the rear feet and the triceratops’s center of mass:
$$
begin{align*}
r_{2} &= dfrac{ F_{2} ~l }{ W } \
&= dfrac{ F_{2} ~ l }{ 3 ~ F_{2} } \
&= dfrac{ l }{ 3} \
&= dfrac{ 3.2 mathrm{~m} }{ 3} \
&= 1.067 mathrm{~m}
end{align*}
$$
So, the distance between the rear feet and the triceratops’s center of mass is $1.067 mathrm{~m}$.
The length of the teeter-totter is $l = 5.2 mathrm{~m}$. The mass that placed at the center of teeter-totter is $m_{1} = 38 mathrm{~kg}$. The vertical force is $F_{2} = 210 mathrm{~N}$. The mass of the child is $m_{c} = 19 mathrm{~kg}$.
$textbf{Required: }$
Finding the distance that the parent push in order to hold the teeter-totter.
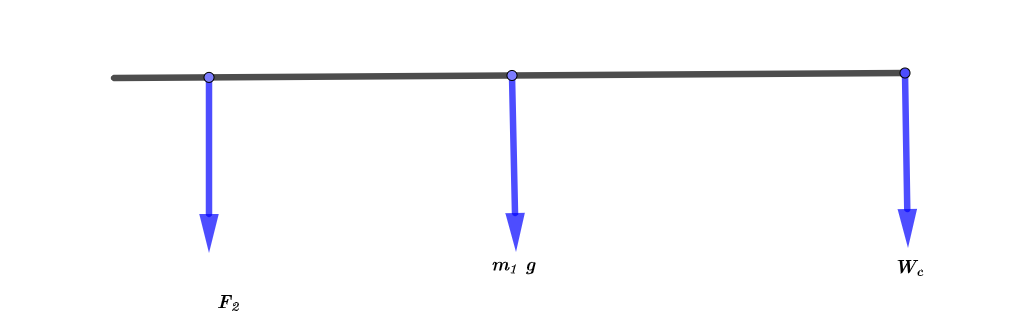
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau &= r ~ F \
end{align*}
$$
In order to evaluate the net torque about the center of the teeter-totter, we use the superposition principle:
$$
begin{align*}
tau_{t} &= r_{1} ~ F_{1} + r_{2} ~ F_{2} + r_{3} ~ F_{3} \
&= 0 – r_{2} ~ F_{2} + r_{3} ~ m_{c} ~ g \
&= – r_{2} ~ F_{2} + r_{3} ~ m_{c} ~ g \
&= 0 \
end{align*}
$$
Rearrange and solve for the distance that the parent push in order to hold the teeter-totter:
$$
begin{align*}
r_{2} &= dfrac{ r_{3} ~ m_{c} ~ g }{ F_{2} } \
&=dfrac{ dfrac{l}{2} ~ m_{c} ~ g }{ F_{2} } \
&= dfrac{ l ~ m_{c} ~ g }{ 2 ~ F_{2} } \
&= dfrac{ 5.23 mathrm{~m} times 19 mathrm{~kg} times 9.8 mathrm{~m/s^{2}} }{ 2 times 210 mathrm{~N} } \
&= 2.319 mathrm{~m}
end{align*}
$$
So, the distance that the parent pushes with the given force in order to hold the teeter-totter is $2.319 mathrm{~m}$.
The length of the remote control is $l = 23 mathrm{~cm}$. The mass of the remote control is $m_{1} = 0.122 mathrm{~kg}$. The required force to operate the power button is $F_{2} = 0.365 mathrm{~N}$. The distance from the power button and the overhanging end is $r’ = 1.41 mathrm{~cm}$.
$textbf{Required: }$
Finding the distance that the remote extend beyond the edge of the table.
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau &= r ~ F \
end{align*}
$$
In order to evaluate the net torque about the center of the teeter-totter, we use the superposition principle:
$$
begin{align*}
tau_{t} &= r_{1} ~ F_{1} + r_{2} ~ F_{2} + r_{3} ~ F_{3} \
&= 0 – r_{2} ~ F_{2} + r_{3} ~ m_{c} ~ g \
&= – r_{2} ~ F_{2} + r_{3} ~ m_{1} ~ g \
&= 0 \
r_{2} ~ F_{2} &= r_{3} ~ m_{1} ~ g \
left( L – r’ right) ~ F_{2} &= left( dfrac{1}{2} – L right) ~ m_{1} ~ g \
L ~ F_{2} – r’ ~ F_{2} &= dfrac{ m_{1} ~ g }{2} – L ~ m_{1} ~ g \
L ~ F_{2} + L ~ m_{1} ~ g &= dfrac{ m_{l} ~ g }{2} + r’ ~ F_{2} \
L ~ left( F_{2} + m_{1} ~ g right) &= dfrac{ m_{1} ~ g }{2} + r’ ~ F_{2} \
end{align*}
$$
Rearrange and solve for the distance that the remote extend beyond the edge of the table:
$$
begin{align*}
L &= dfrac{ dfrac{ m_{1} ~ g ~ l }{2} + r’ ~ F_{2} }{ left( F_{2} + m_{1} ~ g right) } \
&=dfrac{ dfrac{ 0.122 mathrm{~kg} times 9.8 mathrm{~m/s^{2}} times 0.23 mathrm{~m} }{2} + 1.41 times 10^{-2} mathrm{~m} times 0.365 mathrm{~N} }{ left( 0.365 mathrm{~N} + 0.122 mathrm{~kg} times 9.8 mathrm{~m/s^{2}} right) } \
&= 0.0914 mathrm{~m}
end{align*}
$$
So, the distance that the remote extend beyond the edge of the table is $9.14 mathrm{~cm}$.
The mass of the necklace is $m_{2} = 0.086 mathrm{~kg}$. The distance $r_{1}$ equals to $r_{1} = 0.082 mathrm{~m}$. The distance between the balance point and the necklace end is $r_{2} = 0.5 mathrm{~m} – 0.082 mathrm{~m} = 0.418 mathrm{~m}$.
$textbf{Required: }$
(a) Compare between the mass of the meterstick and the necklace.
(b) Finding the meterstick’s mass.
As the problem mentions that the balance point moves toward the necklace end. So, the meterstick’s mass is greater than the necklace’s mass.
As the textbook mentions, the balance point corresponds to zero net torque assigns that
$$
begin{align*}
tau &= F_{1} r_{1} – F_{2} ~ r_{2} \
&= 0 \
m_{1} ~ g ~ r_{1} &= m_{2} ~ g ~ r_{2} \
end{align*}
$$
Rearrange and solve for the distance between the center of mass and the student’s head:
$$
begin{align*}
m_{1} &= dfrac{m_{2} ~ r_{2} }{ r_{1}} \
&= dfrac{ 0.086 mathrm{~kg} times 0.418 mathrm{~m} }{ 0.082 mathrm{~m} } \
&= 0.438 mathrm{~kg}
end{align*}
$$
So, the meterstick’s mass is $0.438 mathrm{~kg}$.
(b) The meterstick’s mass is $0.438 mathrm{~kg}$.
Let the length of the massless rod be $L$. So, the mass $m$ on the left is at a distance $dfrac{L}{2}$ from the axis of rotation, while that on the right is at a distance of $L$ from the axis of rotation. The rod undergoes pure rotation when the mass $m$ is released.
Solve for the left system:
In order to evaluate the angular acceleration of the rod, we use the following relation:
$$
begin{align*}
alpha &= dfrac{ tau }{ I } \
tau &= I ~ alpha_{L} \
r ~ F &= I ~ alpha_{L} \
dfrac{ L}{2} ~ m ~ g &= left( dfrac{L}{2} right)^{2} ~ m ~ alpha_{L} \
end{align*}
$$
Rearrange and solve for the angular acceleration:
$$
begin{align*}
alpha_{L} &= dfrac{2 ~ g }{L} \
end{align*}
$$
Solve for the right system:
In order to evaluate the angular acceleration of the rod, we use the following relation:
$$
begin{align*}
alpha &= dfrac{ tau }{ I } \
tau &= I ~ alpha_{R} \
r ~ F &= I ~ alpha_{R} \
L ~ m ~ g &= L^{2} ~ m ~ alpha_{R} \
end{align*}
$$
Rearrange and solve for the angular acceleration:
$$
begin{align*}
alpha_{R} &= dfrac{ g }{L} \
end{align*}
$$
Therefore, the angular acceleration of the left system is greater than the angular acceleration of the right system $alpha_{L} > alpha_{R}$. Moreover, both systems start from rest. Hence, when the rod on the left reaches the vertical position, the rod on the right doesn’t yet vertical. So, the answer is position (A).
Since the dragonflies complete one revolution each $0.017 mathrm{~s}$. Therefore the angular velocity in terms of $mathrm{~rad/s}$ equals to
$$
begin{align*}
omega &= dfrac{ 1 mathrm{~rev} }{ 0.017 mathrm{~s} } \
&= dfrac{ 1 mathrm{~rev} }{ 0.017 mathrm{~s} } times 2 pi mathrm{~rad} \
&=369.6 mathrm{~rad/s}
end{align*}
$$
So, the angular velocity in terms of $mathrm{~rad/s}$ is $369.6 mathrm{~rad/s}$.
Also, the angular velocity in terms of $mathrm{~rev/min}$ equals to
$$
begin{align*}
omega &= dfrac{ 1 mathrm{~rev} }{ 1 mathrm{~min} } \
&= dfrac{ 1 mathrm{~rev} }{ 0.017 mathrm{~s} } times dfrac{ 60 mathrm{~s} }{ 1 mathrm{~min} } \
&= 3.529 times 10^{3} mathrm{~rev/min}
end{align*}
$$
So, the angular velocity in terms of $mathrm{~rev/min}$ is $3.529 times 10^{3} mathrm{~rev/min}$.
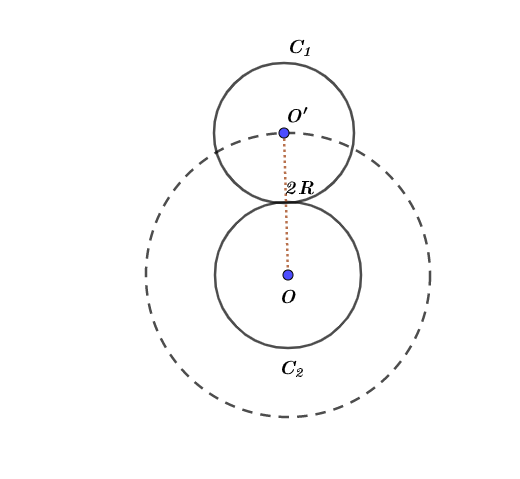
Since the center of the quarter $C_{1}$ moves along a circular path with radius $OO’ = 2 R$, then the total traveled distance by the center is given by
$$
begin{align*}
D &= 2 pi cdot 2 R \
&= 4 pi ~ R \
end{align*}
$$
As the quarter $C_{1}$ rolls without slipping, then the velocity is given by
$$
begin{align*}
v_{CM} &= R ~ omega \
end{align*}
$$
Where, $omega$ is the angular speed of $C_{1}$, and $v_{CM}$ is the linear velocity of center $O’$.
In order to evaluate the distance covered by the center $O’$ in one revolution, we use the following relation:
$$
begin{align*}
v_{CM} &= dfrac{ d }{ T} \
d &= v_{CM} ~ T \
end{align*}
$$
In order to evaluate the peroidic time of the motion in terms of the angular speed, we use the following relation:
$$
begin{align*}
T &= dfrac{ 2 pi }{ omega } \
end{align*}
$$
Rearrange and solve for the distance covered by the center $O’$:
$$
begin{align*}
d &= v_{CM} ~ T \
&= v_{CM} ~ dfrac{ 2 pi }{ omega } \
&= R ~ omega ~ dfrac{ 2 pi }{ omega } \
&= 2 pi ~ R
end{align*}
$$
Which is common sense. In order to evaluate the number of revolutions has rolling quater made about its center, we use the following relation:
$$
begin{align*}
N &= dfrac{ 4 pi ~ R }{ d } \
&= dfrac{ 4 pi ~ R }{ 2 pi ~ R } \
&= boxed{2 mathrm{~revs}}
end{align*}
$$
So, the number of revolutions has rolling quarter made about its center is $2 mathrm{~revs}$.
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
vec{tau} &= vec{r} times vec{F} \
end{align*}
$$
So, the torque is given by the product of force and distance. If the force has a non-zero value and the moment arm (radius) equals zero, then the produced torque equal to zero. But torque can’t produce without a force $tau = r ~ F = r cdot 0 = 0 mathrm{~N cdot m}$. As we see in the previous law, to produce a torque, then the force should be tangential and the distance between the center of the object and the force is $r$. In the case of the force is radial, the produced torque is minimum.
If the force has a non-zero value and the moment arm (radius) equals zero, then the produced torque equal to zero.
The torque can’t produce without a force.
The force should be tangential to get effective torque. In the case of the force is radial, the produced torque is minimum.
The total force is $F_{t} = 1.8 mathrm{~N}$ in the positive $y$ direction. The distance $d$ is $d = 3.2 cdot 10^{-3} mathrm{~m}$. The distance $D$ is $D = 4.5 cdot 10^{-3} mathrm{~m}$.
In order to evaluate the total force, we use the superposition principle by adding the two algebraic values of the forces:
$$
begin{align*}
F_{t} &= F_{1} + F_{2} \
&= 1.8 mathrm{~N} \
F_{2} &= F_{t} – F_{1} \
end{align*}
$$
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau_{t} &= r ~ F_{t} \
&= – F_{1} ~ d + F_{2} ~ left( D – d right) \
&= left( – F_{1} cdot d right) + left( F_{t} – F_{1} right) ~ left( D – d right) \
&= – F_{1} ~ d + F_{t} ~ D – F_{t} ~ d – F_{1} ~ D + F_{1} ~ d \
&= F_{t} ~ D – F_{t} ~ d – F_{1} ~ D \
&= 1.8 mathrm{~N} cdot 4.5 cdot 10^{-3} mathrm{~m} – 1.8 mathrm{~N} cdot 3.2 cdot 10^{-3} mathrm{~m} – F_{1} cdot D \
&= 2.34 cdot 10^{-3} mathrm{~N cdot m} – F_{1} cdot D \
end{align*}
$$
Since the total force must be positive $y$ direction, then the net torque must be positive. So, the tooth may rotate in the anticlockwise direction. The difference between the two distances is equal to $D – d = 4.5 cdot 10^{-3} mathrm{~m} – 3.2 cdot 10^{-3} mathrm{~m} = 1.3 cdot 10^{-3} mathrm{~m}$. Since $d > left( D -d right)$, therefore, the force $F_{2}$ is greater than the force $F_{1}$. So, the answer is (B) $I$ is $F_{2}$, and $II$ is $F_{1}$.
The total force is $F_{t} = 1.8 mathrm{~N}$ in the positive $y$ direction. The distance $d$ is $d = 3.2 cdot 10^{-3} mathrm{~m}$. The distance $D$ is $D = 4.5 cdot 10^{-3} mathrm{~m}$.
Solve for $F_{1} = 0 mathrm{~N}$:
In order to evaluate the total force, we use the superposition principle by adding the two algebraic values of the forces:
$$
begin{align*}
F_{t} &= F_{1} + F_{2} \
&= 1.8 mathrm{~N} \
F_{2} &= F_{t} – F_{1} \
end{align*}
$$
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau_{t} &= r ~ F_{t} \
&= – F_{1} ~ d + F_{2} ~ left( D – d right) \
&= left( – F_{1} cdot d right) + left( F_{t} – F_{1} right) ~ left( D – d right) \
&= – F_{1} ~ d + F_{t} ~ D – F_{t} ~ d – F_{1} ~ D + F_{1} ~ d \
&= F_{t} ~ D – F_{t} ~ d – F_{1} ~ D \
&= 1.8 mathrm{~N} cdot 4.5 cdot 10^{-3} mathrm{~m} – 1.8 mathrm{~N} cdot 3.2 cdot 10^{-3} mathrm{~m} – 0 \
&= 2.34 cdot 10^{-3} mathrm{~N cdot m}
end{align*}
$$
So, the answer is (A) $0.0023 mathrm{~N cdot m}$.
The total force is $F_{t} = 1.8 mathrm{~N}$ in the positive $y$ direction. The distance $d$ is $d = 3.2 cdot 10^{-3} mathrm{~m}$. The distance $D$ is $D = 4.5 cdot 10^{-3} mathrm{~m}$.
In order to evaluate the total force, we use the superposition principle by adding the two algebraic values of the forces:
$$
begin{align*}
F_{t} &= F_{1} + F_{2} \
&= 1.8 mathrm{~N} \
F_{2} &= F_{t} – F_{1} \
end{align*}
$$
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau_{t} &= r ~ F_{t} \
&= – F_{1} ~ d + F_{2} ~ left( D – d right) \
&= left( – F_{1} cdot d right) + left( F_{t} – F_{1} right) ~ left( D – d right) \
&= – F_{1} ~ d + F_{t} ~ D – F_{t} ~ d – F_{1} ~ D + F_{1} ~ d \
&= F_{t} ~ D – F_{t} ~ d – F_{1} ~ D \
&= 1.8 mathrm{~N} cdot 4.5 cdot 10^{-3} mathrm{~m} – 1.8 mathrm{~N} cdot 3.2 cdot 10^{-3} mathrm{~m} – F_{1} cdot D \
&= 2.34 cdot 10^{-3} mathrm{~m} – F_{1} cdot D \
&= 0 mathrm{~N cdot m}
end{align*}
$$
Rearrange and solve for the value of the force $F_{1}$:
$$
begin{align*}
F_{1} &= dfrac{ 2.34 cdot 10^{-3} mathrm{~m} }{ D } \
&= dfrac{ 2.34 cdot 10^{-3} mathrm{~m} }{ 4.5 cdot 10^{-3} mathrm{~m} } \
&= boxed{0.52 mathrm{~N}}
end{align*}
$$
Substituting in the total force equation, then we get
$$
begin{align*}
F_{2} &= F_{t} – F_{1} \
&= 1.8 mathrm{~N} – 0.52 mathrm{~N} \
&= boxed{1.28 mathrm{~N}}
end{align*}
$$
So, the correct answer is (D) $F_{1} = 0.52 mathrm{~N}$, $F_{2} = 1.28 mathrm{~N}$.
The total force is $F_{t} = 1.8 mathrm{~N}$ in the positive $y$ direction. The distance $d$ is $d = 3.2 cdot 10^{-3} mathrm{~m}$. The distance $D$ is $D = 4.5 cdot 10^{-3} mathrm{~m}$.
In order to evaluate the total force, we use the superposition principle by adding the two algebraic values of the forces:
$$
begin{align*}
F_{t} &= F_{1} + F_{2} \
&= 1.8 mathrm{~N} \
F_{2} &= F_{t} – F_{1} \
end{align*}
$$
As the textbook mentions that the torque is given by the product of force and distance
$$
begin{align*}
tau_{t} &= r ~ F_{t} \
&= – F_{1} ~ d + F_{2} ~ left( D – d right) \
&= left( – F_{1} cdot d right) + left( F_{t} – F_{1} right) ~ left( D – d right) \
&= – F_{1} ~ d + F_{t} ~ D – F_{t} ~ d – F_{1} ~ D + F_{1} ~ d \
&= F_{t} ~ D – F_{t} ~ d – F_{1} ~ D \
&= 1.8 mathrm{~N} cdot 4.5 cdot 10^{-3} mathrm{~m} – 1.8 mathrm{~N} cdot 3.2 cdot 10^{-3} mathrm{~m} – F_{1} cdot D \
&= 2.34 cdot 10^{-3} mathrm{~N cdot m} – F_{1} cdot D \
&= 0.0099 mathrm{~N cdot m}
end{align*}
$$
Rearrange and solve for the value of the force $F_{1}$:
$$
begin{align*}
F_{1} &= dfrac{ 2.34 cdot 10^{-3} mathrm{~m} – 0.0099 mathrm{~N cdot m}}{D} \
&= dfrac{ 2.34 cdot 10^{-3} mathrm{~m} – 0.0099 mathrm{~N cdot m}}{ 4.5 cdot 10^{-3} mathrm{~m} } \
&= boxed{-1.68 mathrm{~N}}
end{align*}
$$
Substituting in the total force equation, then we get
$$
begin{align*}
F_{2} &= F_{t} – F_{1} \
&= 1.8 mathrm{~N} + 1.68mathrm{~N} \
&= boxed{3.5 mathrm{~N}}
end{align*}
$$
So, the correct answer is (A) $F_{1} = – 1.7 mathrm{~N}$, $F_{2} = 3.5 mathrm{~N}$.

