
All Solutions
Page 144: Assessment
#### Known
Two vectors are equal is they have the same length (magnitude) and direction, no matter where they are.
—
#### Conclusion
Therefore, from Figure 4.31 we can see that:
$$
begin{align*}
boxed{vec{A}=vec{G}=vec{J}}hspace{0.5cm} tx{and}hspace{0.5cm} boxed{vec{I}=vec{L}}
end{align*}
$$
begin{align*}
boxed{vec{A}=vec{G}=vec{J}}hspace{0.5cm} text{and}hspace{0.5cm} boxed{vec{I}=vec{L}}
end{align*}
$$
#### Known
The magnitude of a vector $vec{A}$ is:
$$
begin{align*}
A=|vec{A}|geq 0, tx{is zero if} vec{A}=vec{0}=0 (tx{null vector})
end{align*}
$$
Note: The above is true only if we are in a Euclidean space. In a Minkowski space the magnitude of a four-vector can be negative.
#### Calculation
Givens: $vec{A}+vec{B}=0$
a)
$$
begin{align*}
&vec{A}+vec{B}=0implies vec{A}=-vec{B}\
&therefore |vec{A}|=|-vec{B}|=|vec{B}|
end{align*}
$$
Therefore the magnitude is equal.
b)
$$
begin{align*}
&vec{A}+vec{B}=0implies vec{A}=-vec{B}hspace{0.5cm} tx{or}hspace{0.5cm} -vec{A}=vec{B}
end{align*}
$$
Therefore $vec{B}$ has opposite direction to $vec{A}$.
—
#### Conclusion
Both vectors have equal magnitude and opposite direction.
$$
begin{align*}
A^{2} &= A_{x}^{2} + A_{y}^{2} \
A_{y}^{2} &= A^{2} – A_{x}^{2} \
A_{y}^{2} &< 0 tag{1}
end{align*}
$$
Equation (1) is impossible, since the square of any number is non negative. The result is a contradiction. Hence, a component of a vector $textbf{can not}$ be greater than the magnitude.
#### Known
A double means the runner reaches second base (A). A triple that the runner reaches third base (B) and a home run that the runner travels all the bases and reaches home (C).
To add two vectors, we place the tail of the second vector on the head of the first vector. The resultant vector is the vector that goes from the tail of the first to the head of the second.
#### Calculation
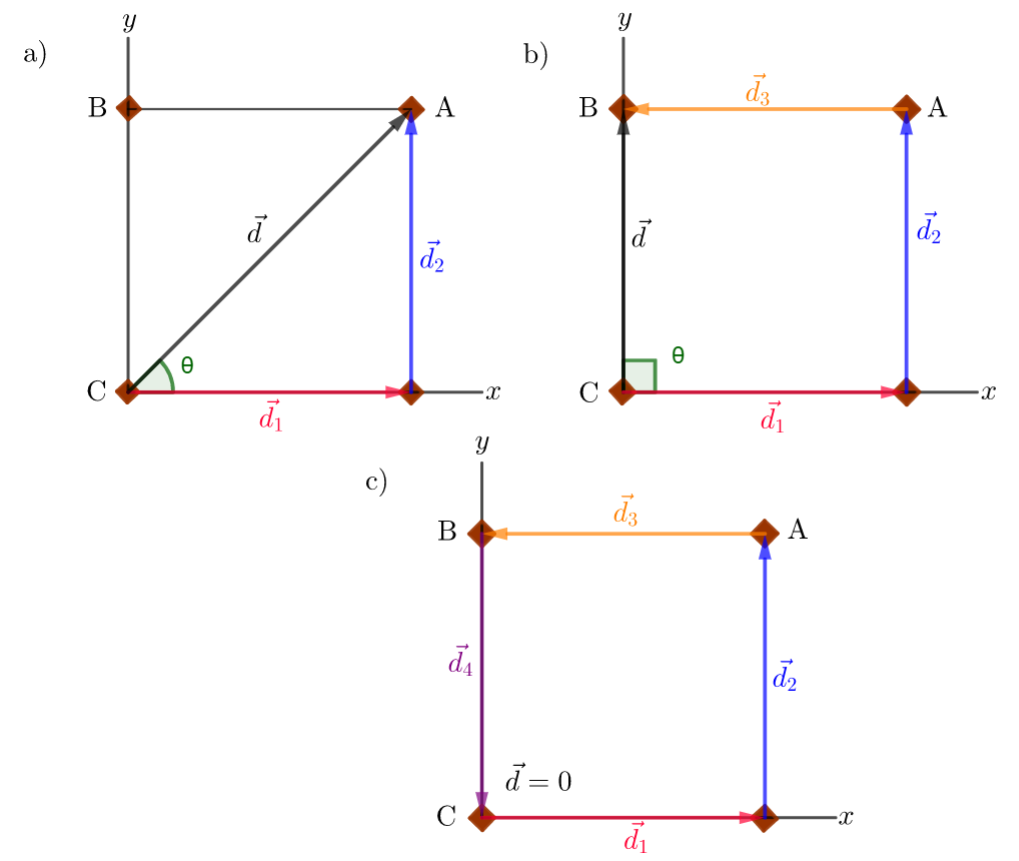
Givens: Figure 4.32.
a) Let $vec{d}_1$ and $vec{d}_2$ be the displacement vectors from home to first base and from first base to second base, respectively. So when we hit a double, the displacement vector is:
$$
begin{align*}
vec{d}=vec{d}_1+vec{d}_2
end{align*}
$$
With $d_1=d_2=27.4 tx{m}$, and $vec{d}_2perpvec{d}_2$ (perpendicular). See Figure a).
Therefore:
$$
begin{align*}
d&=sqrt{d^2_1+d^2_2}, (tx{Pythagorean theorem}),\
&=sqrt{(27.4 tx{m})^2+(27.4 tx{m})^2}\
&=38.7 tx{m}
end{align*}
$$
The direction with respect to the x axis is:
$$
begin{align*}
theta&=tx{tan}^{-1}left(frac{d_2}{d_1}right)=tx{tan}^{-1}left(frac{27.4 cancel{tx{m}}}{27.4 cancel{tx{m}}}right)\
&=45^circ, tx{above the positive x axis.}
end{align*}
$$
b) Let $vec{d}_3$ the displacement vector from second base to third base. So when we hit a triple, the displacement vector is:
$$
begin{align*}
vec{d}=vec{d}_1+vec{d}_2+vec{d}_3
end{align*}
$$
From Figure b) we see that:
$$
begin{align*}
d=27.4 tx{m} tx{and} theta=90^circ
end{align*}
$$
This is easy to see since:
$$
begin{align*}
vec{d}_1=-vec{d}_3implies vec{d}=vec{d}_2
end{align*}
$$
c) Let $vec{d}_4$ be the displacement vector from third base to home plate. So when we hit a home run, the displacement vector is:
$$
begin{align*}
vec{d}&=vec{d}_1+vec{d}_2+vec{d}_3+vec{d}_4\
&=vec{0}=0implies d=0.
end{align*}
$$
Since (see Figure c)):
$$
begin{align*}
vec{d}_1=-vec{d}_3 tx{and} vec{d}_2=-vec{d}_4
end{align*}
$$
—
#### Conclusion
$$
begin{align*}
&tx{a}) boxed{d=38.7 tx{m}}hspace{0.5cm} tx{and} hspace{0.5cm} boxed{theta=45^circ}\
&tx{b}) boxed{d=27.4 tx{m}}hspace{0.5cm} tx{and} hspace{0.5cm} boxed{theta=90^circ}\
&tx{c}) boxed{d=0}
end{align*}
$$
Graphically:
begin{align*}
&text{a}) boxed{d=38.7 text{m}}hspace{0.5cm} text{and} hspace{0.5cm} boxed{theta=45^circ}\
&text{b}) boxed{d=27.4 text{m}}hspace{0.5cm} text{and} hspace{0.5cm} boxed{theta=90^circ}\
&text{c}) boxed{d=0}
end{align*}
$$
#### Known
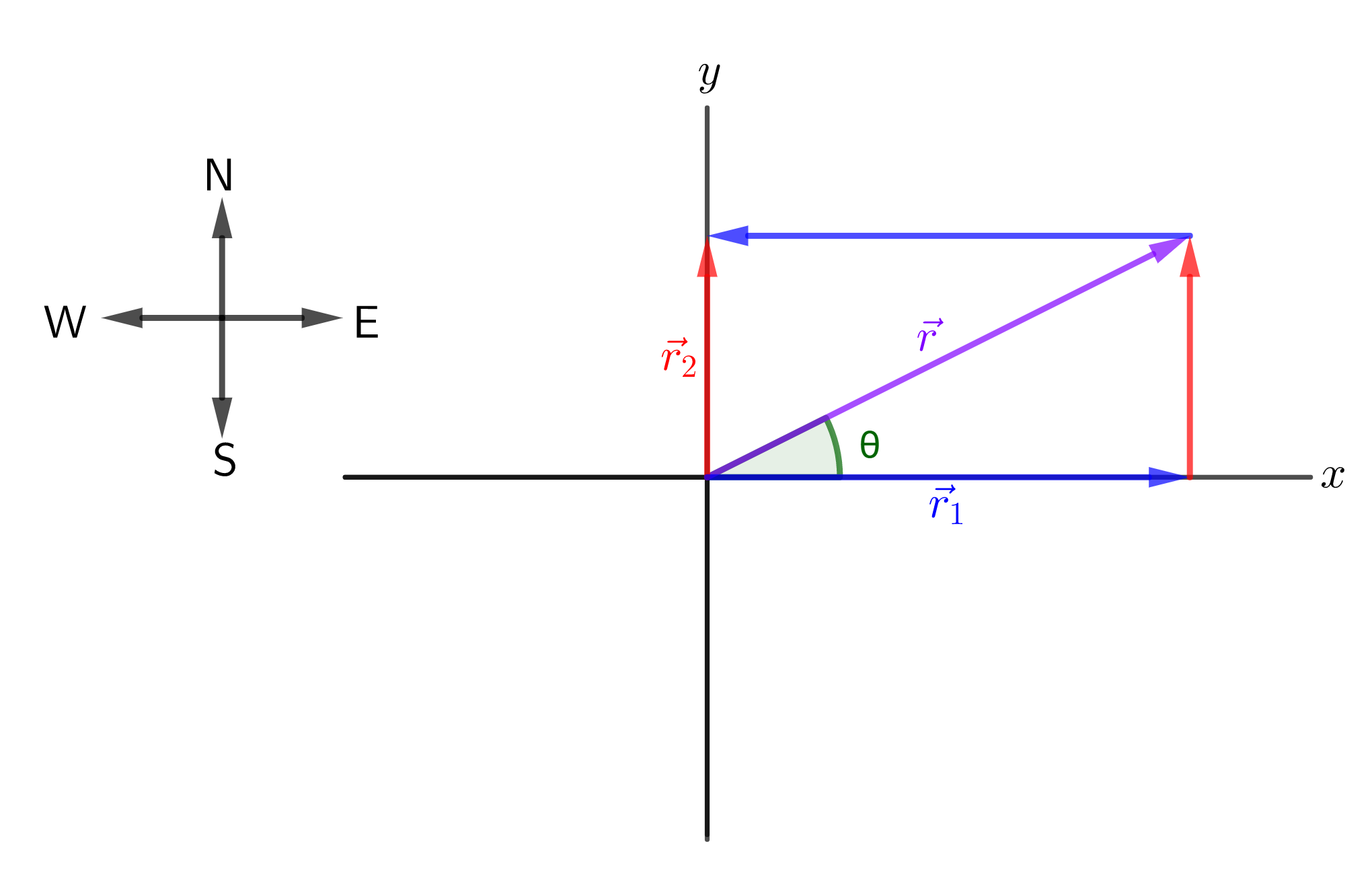
For a vector $vec{r}$, with $r_x$ and $r_y$ components we have:
$$
begin{align}
&r=sqrt{r^2_x+r^2_y}, tx{magnitude}\
&theta=tx{tan}^{-1}left(frac{r_y}{r_x}right), tx{direction angle}
end{align}
$$
#### Calculation
Givens: $r_x=14 tx{m}$, $r_y=-9.5 tx{m}$
From (1) and (2) we have:
a)
$$
begin{align*}
theta&=tx{tan}^{-1}left(frac{-9.5 cancel{tx{m}}}{14 cancel{tx{m}}}right)\
&=-34.2^circ tx{or} 34.2^circ tx{below the posite} x tx{axis}
end{align*}
$$
b)
$$
begin{align*}
r=sqrt{(14 tx{m})^2+(-9.5 tx{m})^2}=16.9 tx{m}
end{align*}
$$
c) For $vec{r’}=(r_x’,r_y’)$, with $r_x’=2r_x$ and $r_y’=2r_y$, we have:
$$
begin{align*}
r’&=sqrt{(r_x’)^2+(r_y’)^2}=sqrt{(2r_x)^2+(2r_y)^2}\
&=sqrt{4left(r_x^2+r_y^2right)}=2sqrt{r_x^2+r_y^2}=2 r
end{align*}
$$
And
$$
begin{align*}
theta’=tx{tan}^{-1}left(frac{r_y’}{r_x’}right)=tx{tan}^{-1}left(frac{cancel{2}r_y}{cancel{2}r_x}right)=theta
end{align*}
$$
—
#### Conclusion
a) $theta=34.2^circ$ below the positive $x$ axis.
b) $r=16.9 tx{m}$
c) Therefore, the magnitude doubles while the direction remains the same.
b) $r=16.9 text{m}$
c) Therefore, the magnitude doubles while the direction remains the same.
#### Known
For a vector $vec{r}$, with $r_x$ and $r_y$ components we have:
$$
begin{align}
&r=sqrt{r^2_x+r^2_y} (tx{magnitude})\
&theta=tx{tan}^{-1}left(frac{r_y}{r_x}right) (tx{direction angle})
end{align}
$$
#### Calculation
Givens: $r_1=680 tx{m}$ to the east, $r_2=340 tx{m}$ to the north.
a)
$$
begin{align*}
vec{r}=vec{r}_1+vec{r}_2
end{align*}
$$
$$
begin{align*}
implies r_x&=r_{1,x}+r_{2,x}, (tx{see figure})\
&=680 tx{m}+0 tx{m}\
&=680 tx{m}
end{align*}
$$
And
$$
begin{align*}
implies r_y&=r_{1,y}+r_{2,y}, (tx{see figure})\
&=0 tx{m}+340 tx{m}\
&=340 tx{m}
end{align*}
$$
Therefore from (1) we have:
$$
begin{align*}
r&=sqrt{r^2_x+r^2_y}=sqrt{(680 tx{m})^2+(340 tx{m})^2}\
&=760 tx{m}
end{align*}
$$
b) From the figure we see that the direction is roughly $30^circ$ north of east because the side opposite the angle is about half the value of the hypotenuse (magnitude of $vec{r}$), and we know that:
$$
begin{align*}
tx{sin}(30^circ)=frac{tx{opposite side}}{tx{hypotenuse}}=frac{1}{2}
end{align*}
$$
c) From (2) we have:
$$
begin{align*}
theta&=tx{tan}^{-1}left(frac{r_y}{r_x}right)=tx{tan}^{-1}left(frac{340 cancel{tx{m}}}{680 cancel{tx{m}}}right)\
&=26.6^circ
end{align*}
$$
—
#### Conclusion
a) $r=760 tx{m}$.
b) From the figure, the direction is about $30^circ$.
c) $theta=26.6^circ$.
b) From the figure, the direction is about $30^circ$.
c) $theta=26.6^circ$.
So A has the greater x component.
The y component of B = – 120*sin70° = -112,76
Since the y component of A = 0,
So A has greater y component
#### Known
The magnitude and direction of a vector $vec{d}$ are given by:
$$
begin{align}
&d=sqrt{d_x^2+d_y^2}\
&theta=tx{tan}^{-1}left(frac{d_y}{d_x}right)
end{align}
$$
Where $d_x$ and $d_y$ are the components of the vector $vec{d}$ and $theta$ is the angle that the vector makes with respect to the $x$ axis.
#### Calculation
The figures show the four possible vectors of displacement to the treasure.
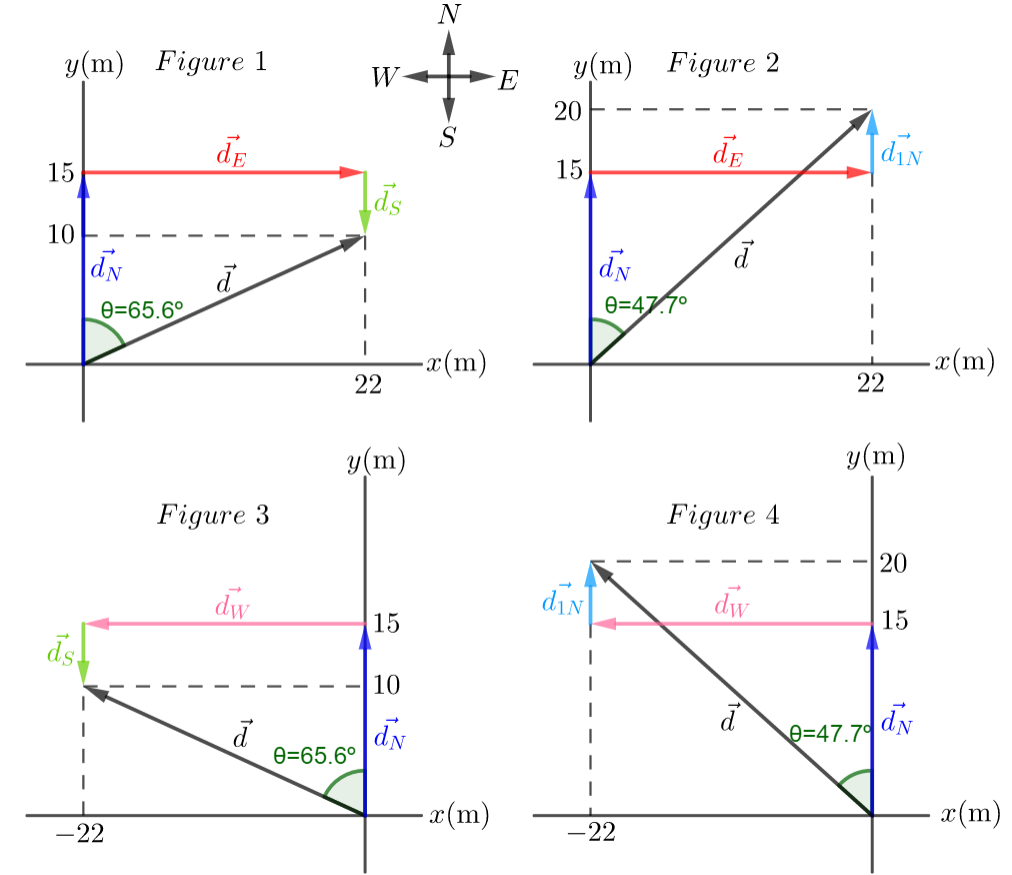
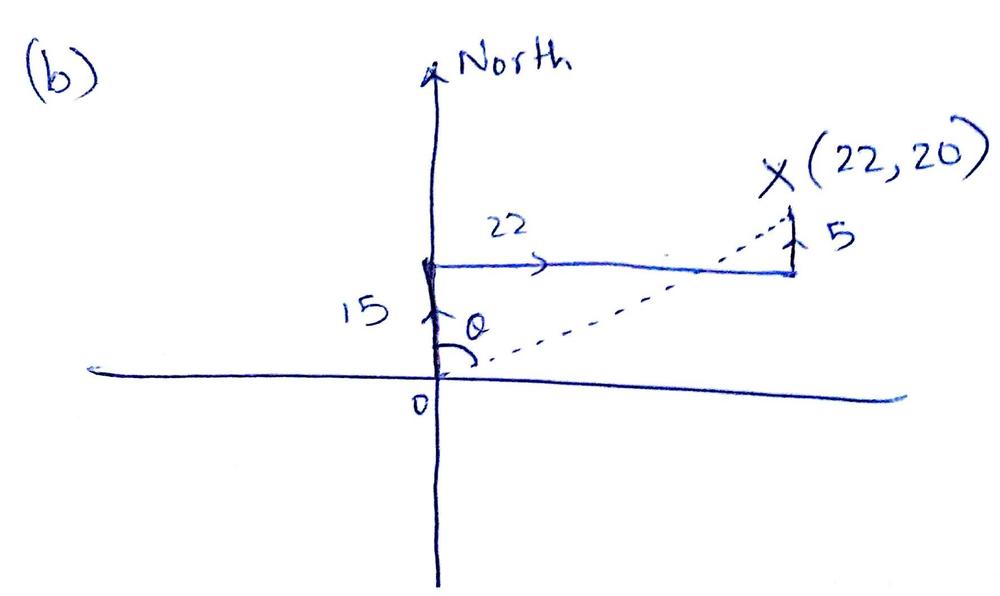
Figure 1 shows the displacement to the north, then east, and then south. The resulting vector is the sum of these three vectors. In components this is:
$$
begin{align*}
&vec{d}=vec{d}_N+vec{d}_E+vec{d}_S\
implies &d_x=d_{N,x}+d_{E,x}+d_{S,x}=0 tx{m}+22 tx{m}+0 tx{m}=22 tx{m}\
&d_y=d_{N,y}+d_{E,y}+d_{S,y}=15 tx{m}+0 tx{m}-5 tx{m}=10 tx{m}\
therefore &vec{d}=left(d_x, d_yright)=(22 tx{m}, 10 tx{m})\
implies &d=sqrt{(22 tx{m})^2+(10 tx{m})^2}=24.17 tx{m}
end{align*}
$$
We have to give the direction relative to the north ($y$-axis). So instead of the expression (2) we can use:
$$
begin{align*}
theta_N=tx{tan}^{-1}left(frac{d_x}{d_y}right)=tx{tan}^{-1}left(frac{22 cancel{tx{m}}}{10 cancel{tx{m}}}right)=65.6^circ tx{east of north}
end{align*}
$$
Remember that $tx{tan}(theta)=frac{tx{opposite side}}{tx{adjacent side}}$.
If we use expression (2), then to obtain the direction with respect to north we do:
$$
begin{align*}
theta_N&=90^circ-theta=90^circ-tx{tan}^{-1}left(frac{d_y}{d_x}right)\
&=90^circ-tx{tan}^{-1}left(frac{10 cancel{tx{m}}}{22 cancel{tx{m}}}right)=65.6^circ
end{align*}
$$
Figure 2 shows the displacement to the north, then east, and then north.
The total displacement is:
$$
begin{align*}
&vec{d}=vec{d}_N+vec{d}_E+vec{d}_{1N}, tx{with} d_{1N}=5 tx{m}\
implies &d_x=d_{N,x}+d_{E,x}+d_{1N,x}=0 tx{m}+22 tx{m}+0 tx{m}=22 tx{m}\
&d_y=d_{N,y}+d_{E,y}+d_{1N,y}=15 tx{m}+0 tx{m}+5 tx{m}=20 tx{m}\
therefore &vec{d}=left(d_x, d_yright)=(22 tx{m}, 20 tx{m})\
implies &d=sqrt{(22 tx{m})^2+(20 tx{m})^2}=29.73 tx{m}
end{align*}
$$
The direction relative to north is:
$$
begin{align*}
theta_N=tx{tan}^{-1}left(frac{d_x}{d_y}right)=tx{tan}^{-1}left(frac{22 cancel{tx{m}}}{20 cancel{tx{m}}}right)=47.7^circ tx{east of north}
end{align*}
$$
Figure 3 shows the displacement to north, then west and then south.
The total displacement is:
$$
begin{align*}
&vec{d}=vec{d_N}+vec{d_W}+vec{d_{S}}\
implies &d_x=d_{N,x}+d_{W,x}+d_{S,x}=0 tx{m}-22 tx{m}+0 tx{m}=-22 tx{m}\
&d_y=d_{N,y}+d_{W,y}+d_{S,y}=15 tx{m}+0 tx{m}-5 tx{m}=10 tx{m}\
therefore &vec{d}=left(d_x, d_yright)=(-22 tx{m}, 10 tx{m})\
implies &d=sqrt{(-22 tx{m})^2+(10 tx{m})^2}=24.17 tx{m}
end{align*}
$$
The direction relative to north is:
$$
begin{align*}
theta_N=tx{tan}^{-1}left(frac{d_x}{d_y}right)=tx{tan}^{-1}left(frac{-22 cancel{tx{m}}}{10 cancel{tx{m}}}right)=-65.6^circ tx{or} 65.6^circ tx{west of north}
end{align*}
$$
Figure 4 shows the displacement to north, then west, and then north.
The total displacement is:
$$
begin{align*}
&vec{d}=vec{d}_N+vec{d}_W+vec{d}_{1N}, tx{with} d_{1N}=5 tx{m}\
implies &d_x=d_{N,x}+d_{W,x}+d_{1N,x}=0 tx{m}-22 tx{m}+0 tx{m}=-22 tx{m}\
&d_y=d_{N,y}+d_{W,y}+d_{1N,y}=15 tx{m}+0 tx{m}+5 tx{m}=20 tx{m}\
therefore &vec{d}=left(d_x, d_yright)=(-22 tx{m}, 20 tx{m})\
implies &d=sqrt{(-22 tx{m})^2+(20 tx{m})^2}=29.73 tx{m}
end{align*}
$$
the direction relative to north is:
$$
begin{align*}
theta_N=tx{tan}^{-1}left(frac{d_x}{d_y}right)=tx{tan}^{-1}left(frac{-22 cancel{tx{m}}}{20 cancel{tx{m}}}right)=-47.7^circ tx{or} 47.7^circ tx{west of north}
end{align*}
$$
—
#### Conclusion
The four possible locations are:
1-) $d=24.17 tx{m}$ and $theta=65.6^circ$ east of north.
2-) $d=29.73 tx{m}$ and $theta=47.7^circ$ east of north.
3-) $d=24.17 tx{m}$ and $theta=65.6^circ$ west of north.
4-) $d=29.73 tx{m}$ and $theta=47.7^circ$ west of north.
2-) $d=29.73 text{m}$ and $theta=47.7^circ$ east of north.
3-) $d=24.17 text{m}$ and $theta=65.6^circ$ west of north.
4-) $d=29.73 text{m}$ and $theta=47.7^circ$ west of north.
Direction angle relative to north direction $theta = tan^{-1}left(dfrac{22}{10} right) = 65.56^{0}$
Direction angle relative to north direction $theta = tan^{-1}left(dfrac{22}{20} right) = 47.73^{0}$
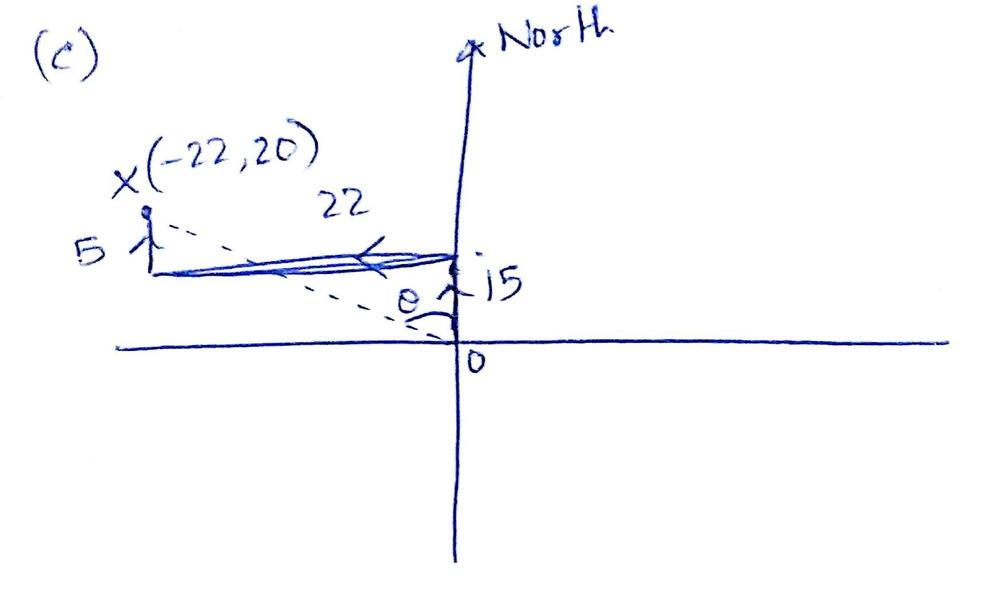
Direction angle relative to north direction $theta = tan^{-1}left(dfrac{-22}{20} right) = -47.73^{0}$
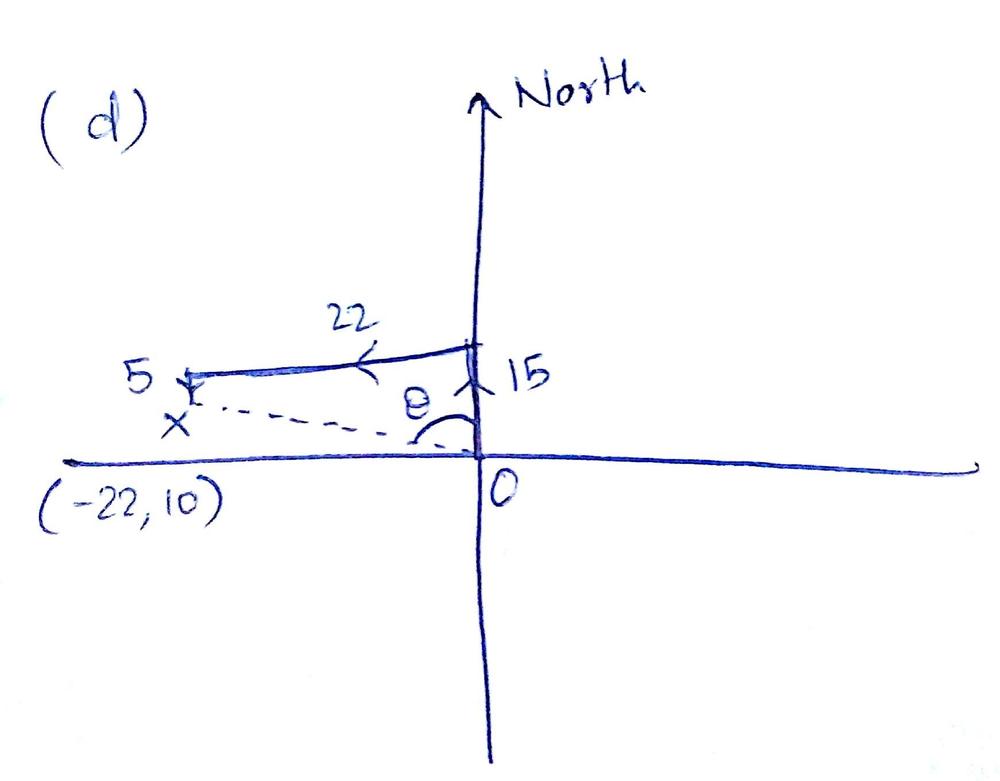
Direction angle relative to north direction $theta = tan^{-1}left(dfrac{-22}{10} right) = -65.56^{0}$
#### Known
The components of vector $vec{v}$ on the $x$ axis and on the $y$ axis are determined as:
$$
begin{align}
r_x=r tx{cos}(theta)hspace{0.5cm}tx{and}hspace{0.5cm} r_y=r tx{sin}(theta)
end{align}
$$
These components tell us the size of the vector in the $x$ direction (the absolute value of the component) and in the $y$ direction.
#### Calculation
Givens: $theta=20.0^circ$ below the horizontal. $r=150 tx{m}$.
From (1), we have:
a)
$$
begin{align*}
r_y=(-150 tx{m}) tx{sin}(20.0^circ)=-51.30 tx{m}
end{align*}
$$
The negative sign is because we are considering the zero on the surface and the negative direction down.
b)
$$
begin{align*}
r_x=(150 tx{m}) tx{cos}(20.0^circ)=140.95 tx{m}
end{align*}
$$
—
#### Conclusion
a) The whale is $51.30 tx{m}$ deep.
b) The whale has traveled a horizontal distance of $140.95 tx{m}$.
b) The whale has traveled a horizontal distance of $140.95 text{m}$.
#### Known
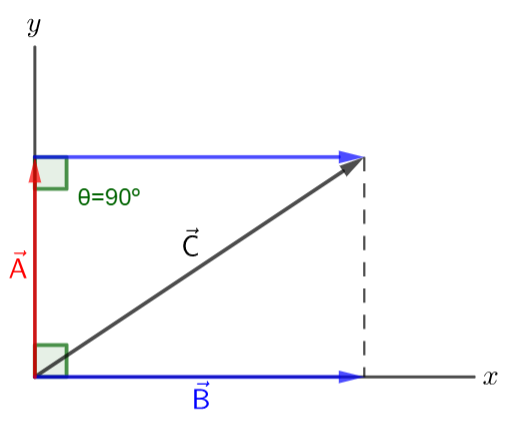
The magnitude of the sum of two vector is equal to the length of the side of the triangle that is formed by this sum.
Therefore if we have:
$$
begin{align*}
&vec{C}=vec{A}+vec{B}\
&implies C^2=A^2+B^2+2AB tx{cos}(theta)
end{align*}
$$
Where $theta$ is the angle between the two vectors (two adjacent sides of the formed triangle). Hence:
$$
begin{align*}
C^2=A^2+B^2implies theta=90^circ
end{align*}
$$
—
#### Conclusion
The vectors are perpendicular to each other.
graphically:
||a|| + ||b|| >= ||a+b||
This means that the sum of the lengths of two sides of a triangle is always greater than the length of the third side because the shortest distance between two points is a straight line and we will have to make a turn to follow two sides of a triangle. The only way that ||a|| + ||b|| = ||a+b|| is if a and b don’t make a triangle at all. If they form a straight line, then obviously the sum of their lengths is the length of the whole line. So a and b point in the same direction
#### Known
If we have $vec{A}$ and $vec{B}$, then:
$$
begin{align}
vec{C}=vec{A}+vec{B}implies C_x&=A_x+B_x\
C_y&=A_y+B_y
end{align}
$$
#### Calculation
Givens: $A=40.0 tx{m}$ and $theta=20.0^circ$ below the positive $x$ axis. $B=75.0 tx{m}$ and $theta=50.0^circ$ above the positive $x$ axis.
The components of $vec{A}$ and $vec{B}$ are given by:
$$
begin{align*}
&A_x=A tx{cos}(theta)=(40.0 tx{m}) tx{cos}(20.0^circ)=37.6 tx{m}\
&A_y=A tx{sin}(theta)=(-40.0 tx{m}) tx{sin}(20.0^circ)=-13.7 tx{m}
end{align*}
$$
The negative sign is because the component is below the $x$ axis.
$$
begin{align*}
&B_x=B tx{cos}(theta)=(75.0 tx{m}) tx{cos}(50.0^circ)=48.2 tx{m}\
&B_y=B tx{sin}(theta)=(75.0 tx{m}) tx{sin}(50.0^circ)=57.5 tx{m}
end{align*}
$$
From (1) and (2) we have:
$$
begin{align*}
&C_x=37.6 tx{m}+48.2 tx{m}=85.8 tx{m}
&C_y=-13.7 tx{m}+57.5 tx{m}=43.8 tx{m}
end{align*}
$$
$$
begin{align*}
theta=tx{tan}^{-1}left(frac{C_y}{C_x}right)=tx{tan}^{-1}left(frac{43.8 cancel{tx{m}}}{85.8 cancel{tx{m}}}right)=27.0^circ
end{align*}
$$
—
#### Conclusion
$$
begin{align*}
vec{C}=(C_x,C_y)=(85.8 tx{m},43.8 tx{m})
end{align*}
$$
begin{align*}
boxed{vec{C}=(C_x,C_y)=(85.8 text{m},43.8 text{m})}
end{align*}
$$
To add two vectors, we place the tail of the second vector on the head of the first vector. The resultant vector is the vector that goes from the tail of the first to the head of the second. Always keeping the directions of the vectors and their lengths.
### Givens:
– $A=75 text{m}$
– $vec{C}=vec{A}+vec{B}=95 text{m}$

The exact result is computed using the formula:
$$begin{align*}B&=sqrt{C^2+A^2}\&=sqrt{95^2 +75^2}\&=121text{ m}end{align*}$$
The direction of $vec{B}$ is roughly $52^circ$ on the $x$-axis in the negative direction. This is because side $C$ is greater than side $A$, so the angle of $vec{B}$ would be between $45^circ$ (if $A=C$) and $90^circ$.
The exact result is computed using the formula:
$$begin{align*}
theta&=tan^{-1}left(frac{C}{A}right)\
&= tan^{-1}bigg(frac{95}{75} bigg)\
&=boxed{51.7degree}
end{align*}$$
Vector $vec{B}$ has a magnitude roughly of $121 text{m}$ and points in the direction $58degree$ above the $x$-axis in the negative direction.
$theta=52degree$
#### Known
If we have $vec{A}$ and $vec{B}$, then:
$$
begin{align}
vec{C}=vec{A}+vec{B}implies C_x&=A_x+B_x\
C_y&=A_y+B_y
end{align}
$$
#### Calculation
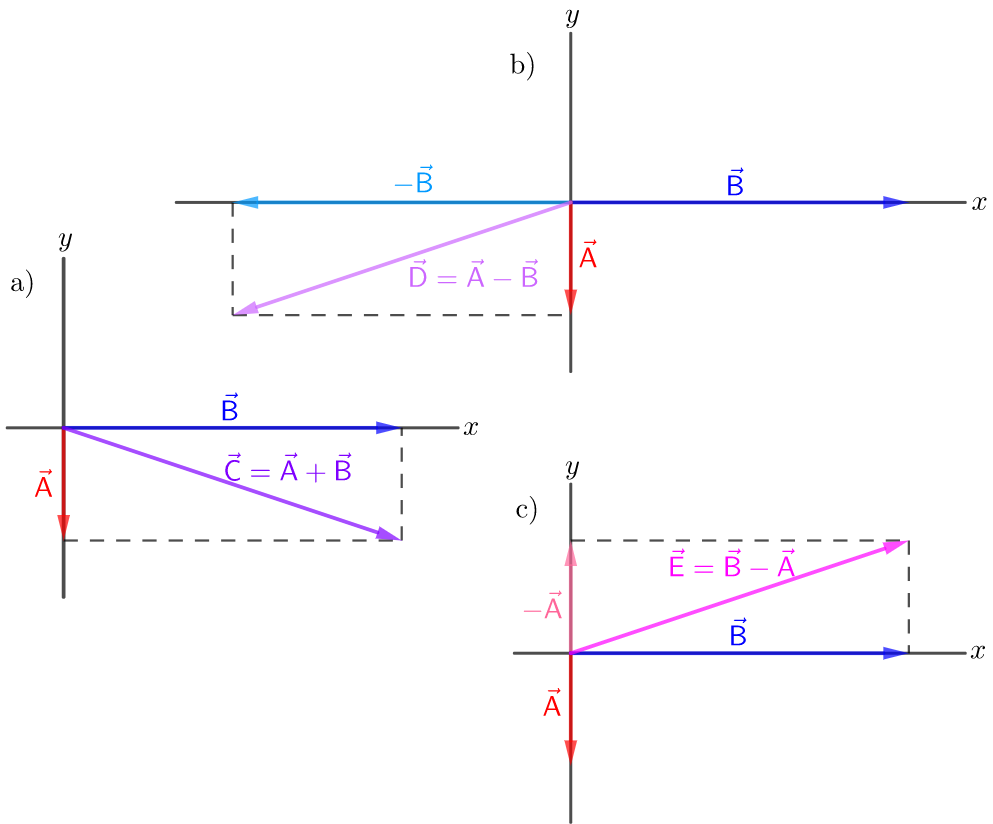
Givens: $A=5 tx{km}$ in the negative $y$ direction, this is $vec{A}=(0 tx{km}, -5 tx{km})$. $B=15.0 tx{km}$ in the positive $x$ direction, this is $vec{B}=(15 tx{km}, 0 tx{km})$.
From (1) and (2) we have:
a)
$$
begin{align*}
vec{C}=vec{A}+vec{B}implies C_x&=A_x+B_x\
&=0 tx{km}+15 tx{km}=15 tx{km}\
C_y&=A_y+B_y\
&=-5 tx{km}+0 tx{km}=-5 tx{km}
end{align*}
$$
$$
begin{align*}
therefore &vec{C}=(C_x, C_y)=(15 tx{km}, -5 tx{km})\
implies &C=sqrt{C_x^2+C_y^2}=sqrt{(15 tx{km})^2+(-5 tx{km})^2}=15.8 tx{km}approx 16 tx{km}
end{align*}
$$
b)
$$
begin{align*}
vec{D}=vec{A}-vec{B}implies D_x&=A_x-B_x\
&=0 tx{km}-15 tx{km}=-15 tx{km}\
D_y&=A_y-B_y\
&=-5 tx{km}-0 tx{km}=-5 tx{km}
end{align*}
$$
$$
begin{align*}
therefore &vec{D}=(D_x, d_y)=(-15 tx{km}, -5 tx{km})\
implies &D=sqrt{D_x^2+D_y^2}=sqrt{(-15 tx{km})^2+(-5 tx{km})^2}=15.8 tx{km}approx 16 tx{km}
end{align*}
$$
c)
$$
begin{align*}
vec{E}&=vec{B}-vec{A}=-1(vec{A}-vec{B})=-vec{D}\
&implies E=D=15.8 tx{km}approx 16 tx{km}
end{align*}
$$
Likewise, $vec{B}-vec{A}$ can be found in the same way as in the previous sections.
—
#### Conclusion
$$
begin{align*}
boxed{|vec{A}+vec{B}|=|vec{A}-vec{B}|=|vec{B}-vec{A}|=16 tx{km}}
end{align*}
$$
Graphically:
begin{align*}
boxed{|vec{A}+vec{B}|=|vec{A}-vec{B}|=|vec{B}-vec{A}|=16 text{km}}
end{align*}
$$
#### Known
We can calculate the magnitude of a vector $vec{r}=(r_x, r_y)$ and its direction as:
$$
begin{align}
r=sqrt{r_x^2+r_y^2}hspace{0.5cm} tx{and}hspace{0.5cm} theta=tx{tan}^{-1}left(frac{r_y}{r_x}right)
end{align}
$$
#### Calculation
Givens: $A=220 tx{km}$ and $theta=32^circ$ north of west. $B=140 tx{km}$ and $theta=65^circ$ east of north.
a)
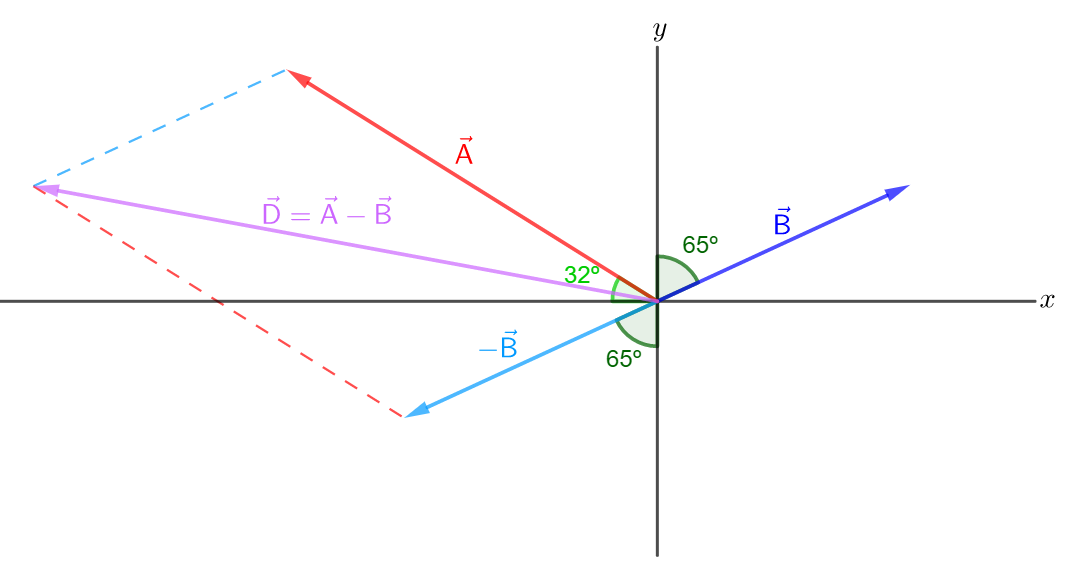
b)
$$
begin{align}
vec{D}=vec{A}-vec{B}implies D_x&=A_x-B_x\
D_y&=A_y-B_y
end{align}
$$
With:
$$
begin{align*}
A_x&=A tx{cos}(theta)=(-220 tx{km}) tx{cos}(32^circ)\
&=-186.6 tx{km}\
B_x&=B tx{cos}(90^circ-theta)=(140 tx{km}) tx{cos}(90^circ-65^circ)=(140 tx{km}) tx{cos}(25^circ)=\
&=(140 tx{km}) tx{sin}(65^circ)=126.9 tx{km}\
A_y&=A tx{sin}(theta)=(220 tx{km}) tx{sin}(32^circ)\
&=116.6 tx{km}\
B_y&=B tx{sin}(90^circ-theta)=(140 tx{km}) tx{sin}(90^circ-65^circ)=(140 tx{km}) tx{sin}(25^circ)\
&=59.2 tx{km}
end{align*}
$$
Therefore from (2) and (3):
$$
begin{align*}
D_x&=-186.6 tx{km}-126.9 tx{km}=-313.5 tx{km}\
D_y&=116.6 tx{km}-59.2 tx{km}=57.4 tx{km}\
implies D&=sqrt{D_x^2+D_y^2}=sqrt{(-313.5 tx{km})^2+(57.4 tx{km})^2}=319 tx{km}\
theta&=tx{tan}^{-1}left(frac{D_y}{D_x}right)=tx{tan}^{-1}left(frac{57.4 cancel{tx{km}}}{-313.5 cancel{tx{km}}}right)=169.6^circ
end{align*}
$$
Relative to the east (positive $x$ axis), or $169.6^circ-90^circ=79.6^circ$ west of north.
—
#### Conclusion
Vector $vec{D}$ has a magnitude of $319 tx{km}$ and points in the direction $79.6^circ$ west of north.
#### Known
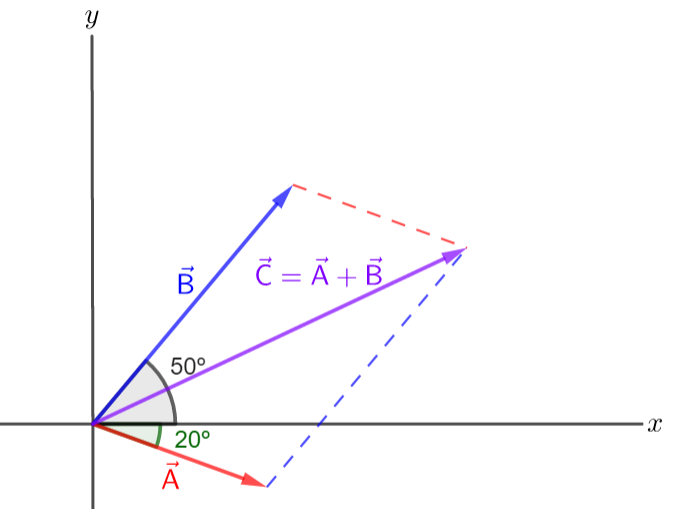
To add two vectors, we place the tail of the second vector on the head of the first vector. The resultant vector is the vector that goes from the tail of the first to the head of the second. Always keeping the directions of the vectors and their lengths.
If we have:
$$
begin{align*}
&vec{R}=vec{R}_1+vec{R}_2\
implies &R_x=R_{1,x}+R_{2,x}hspace{0.5cm}tx{and}hspace{0.5cm} R_y=R_{1,y}+R_{2,y}
end{align*}
$$
#### Calculation
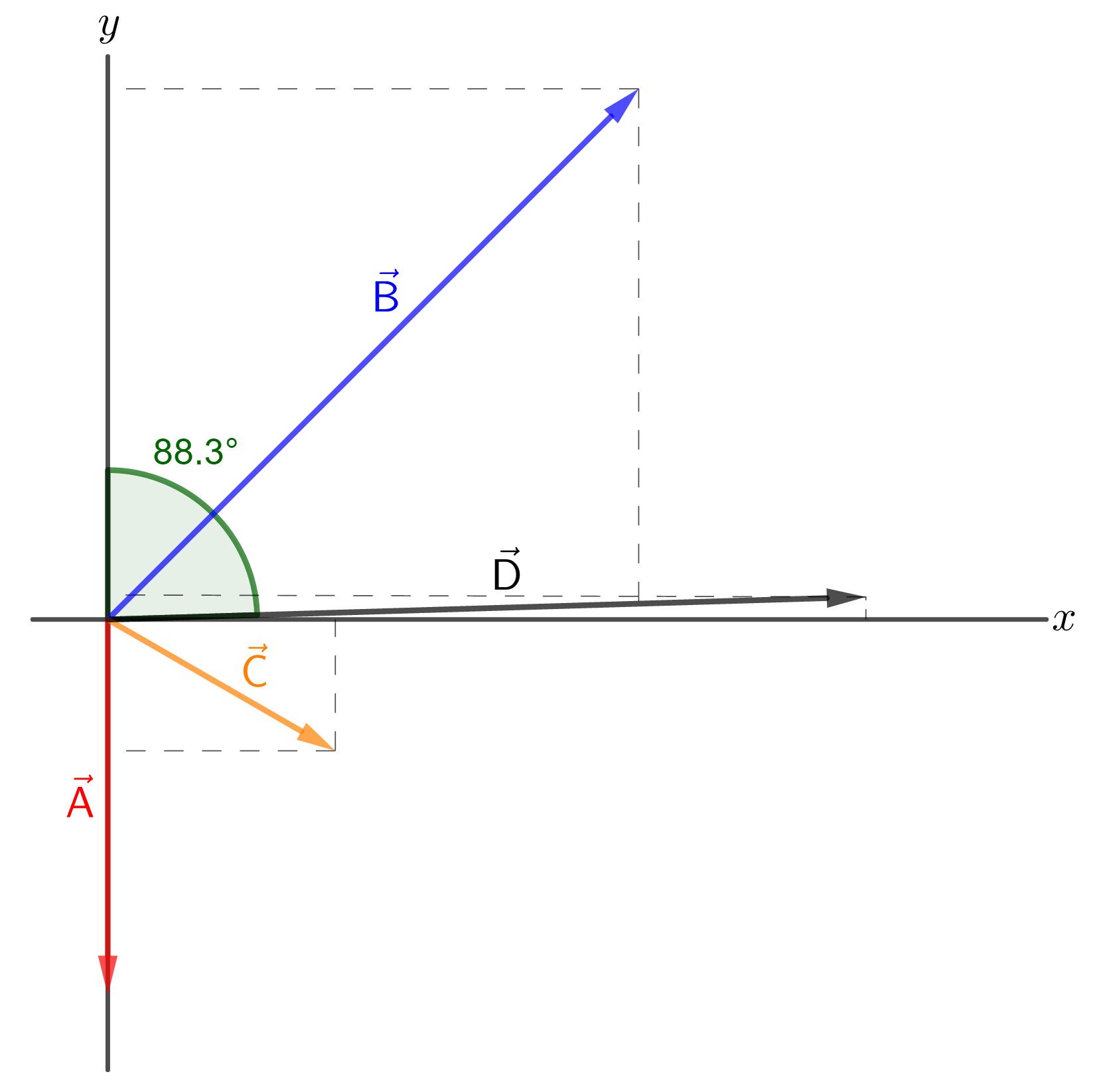
Givens: Figure 4.34. $A=10.0 tx{m}$. $B=20.0 tx{m}$. $C=7.0 tx{m}$.
a) The figure shows the displacement resulting from the three displacements $vec{A}$, $vec{B}$ and $vec{C}$, that is
$vec{D}=vec{A}+vec{B}+vec{C}$.
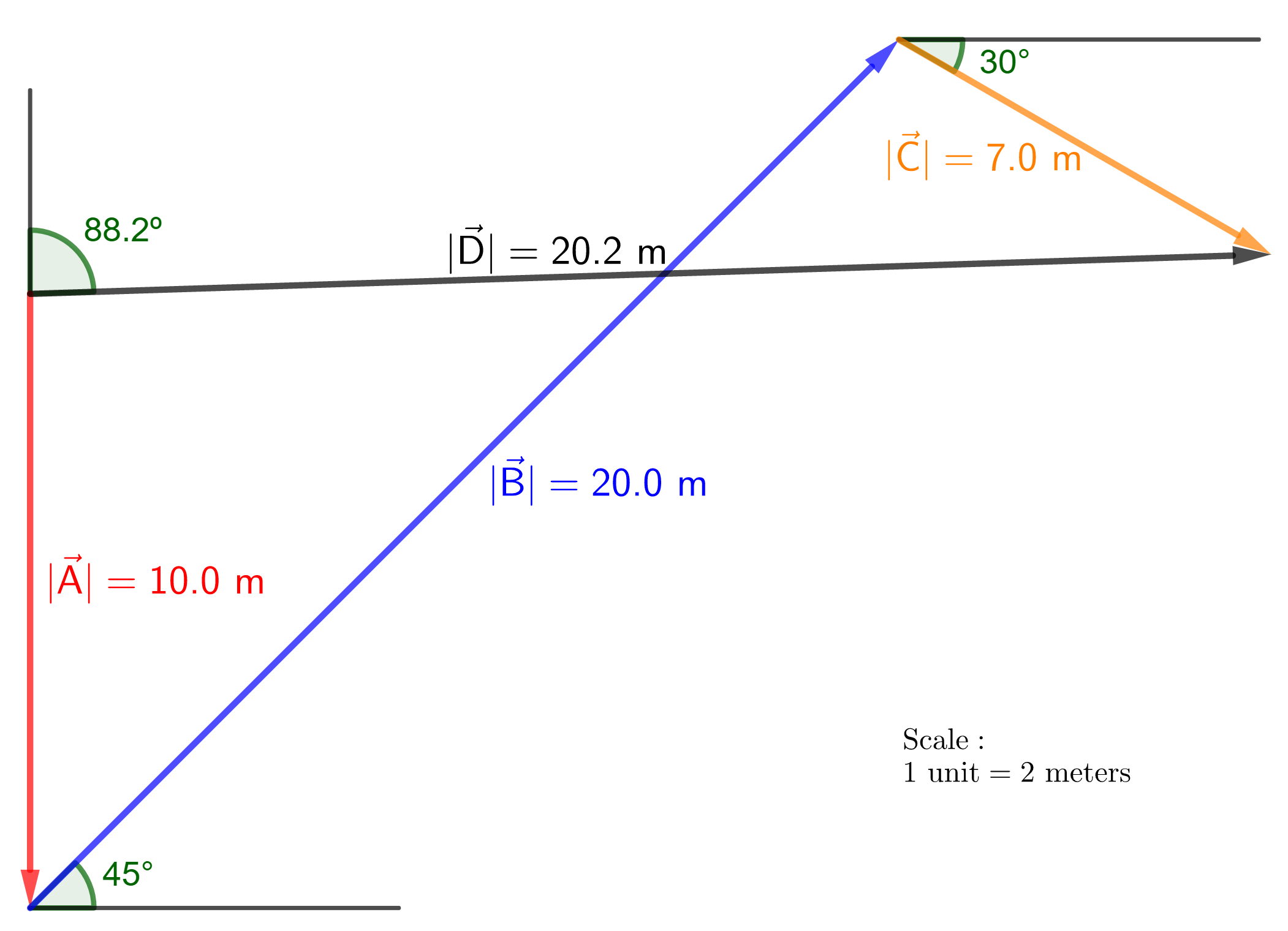
This method allows us to solve the resulting vector (determine its magnitude and direction) without having to do any calculations, just following the rule of the sum of vectors and using a representative scale to be able to draw the vectors properly.
If we choose the $x$-axis as the longest side of the court and the $y$-axis as the shortest side of the court, we can write the vectors in components as follows:
b)
$$
begin{align*}
vec{A}=(A_x, A_y)=(0 tx{m}, -10 tx{m})
end{align*}
$$
The negative sign is because $vec{A}$ points in the negative direction (the one we have chosen as negative).
$$
begin{align*}
vec{B}&=(B_x, B_y)=(B tx{cos} theta, B tx{sin} theta)\
&=((20 tx{m}) tx{cos}(45^circ), (20 tx{m}) tx{sin}(45^circ))\
&=(14.1 tx{m}, 14.1 tx{m})\
vec{C}&=(C_x, C_y)=(C tx{cos} theta, C tx{sin} theta)\
&=((7 tx{m}) tx{cos}(30^circ), (-7 tx{m}) tx{sin}(30^circ))\
&=(6.1 tx{m}, -3.5 tx{m})
end{align*}
$$
The negative sign is because $vec{C}$ points $30^circ$ below the $x$-axis, that is, negative direction.
Therefore, the resulting displacement vector is:
$$
begin{align*}
&vec{D}=vec{A}+vec{B}+vec{C}\
implies D_x&=A_x+B_x+C_x=0 tx{m}+14.1 tx{m}+6.1 tx{m}\
&=20.2 tx{m}\
implies D_y&=A_y+B_y+C_y=-10 tx{m}+14.1 tx{m}-3.5 tx{m}\
&=0.6 tx{m}\
implies vec{D}&=(20.2 tx{m}, 0.6 tx{m})\
therefore D&=sqrt{D_x^2+D_y^2}=sqrt{(20.2 tx{m})^2+(0.6 tx{m})^2}\
&boxed{D=20.2 tx{m}}
end{align*}
$$
And points in the direction:
$$
begin{align*}
theta&=tx{tan}^{-1}left(frac{D_y}{D_x}right)=tx{tan}^{-1}left(frac{0.6 cancel{tx{m}}}{20.2 cancel{tx{m}}}right)\
&=1.70^circ
end{align*}
$$
Vector $vec{D}$ points in the direction $1.70^circ$ above the positive $x$-axis, or $90^circ-1.70^circboxed{=88.3^circ}$ to the right of the positive $y$-axis.
Graphically:
—
#### Conclusion
a) $D=20.2 tx{m}$ and $theta=88.2^circ$ to the right of the positive $y$-axis.
b) $D=20.2 tx{m}$ and $theta=88.3^circ$ to the right of the positive $y$-axis.
The small angle difference is due to the number of significant figures used in the calculations.
b) $D=20.2 text{m}$ and $theta=88.3^circ$ to the right of the positive $y$-axis.
#### Known
The movement of objects is relative, it depends on the reference system from where it is being observed.
When we are sailing against the wind, we feel them stronger because it moves with a speed with respect to us (or we with respect to the wind) equal to the speed of the boat plus the speed of the wind, these speeds measured for example with relation to water. This is:
$$
begin{align*}
vec{v}_{tx{bw}}=vec{v}_{tx{ba}}+(-vec{v}_{tx{aw}})
end{align*}
$$
Where $vec{v}_{tx{bw}}$ is the speed of the boat in relation to the water, $vec{v}_{tx{ba}}$ is the speed of the boat in relation to the air (wind) and $vec{v}_{tx{aw}}$ is the speed of the air (wind) in relation to the water. The negative sign of $vec{v}_{tx{aw}}$ is due to the fact that the wind is going in the opposite direction to the speed of the boat $vec{v}_{tx{bw}}$.
Therefore:
$$
begin{align*}
&vec{v}_{tx{ba}}=vec{v}_{tx{bw}}+vec{v}_{tx{aw}}\
implies &boxed{v_{tx{ba}}=v_{tx{bw}}+v_{tx{aw}}}
end{align*}
$$
For example if $v_{tx{bw}}=6.5 frac{tx{m}}{tx{s}}$ and $v_{tx{aw}}=2.5 frac{tx{m}}{tx{s}}$, we would feel a wind of:
$$
begin{align*}
v_{tx{ba}}=6.5 frac{tx{m}}{tx{s}}+2.5 frac{tx{m}}{tx{s}}=9.0 frac{tx{m}}{tx{s}}
end{align*}
$$
In case of sailing downwind, we feel it less strong, since the wind speed in relation to us is the speed of the boat minus the wind speed, that is:
$$
begin{align*}
&vec{v}_{tx{bw}}=vec{v}_{tx{ba}}+vec{v}_{tx{aw}}\
implies &vec{v}_{tx{ba}}=vec{v}_{tx{bw}}-vec{v}_{tx{aw}}\
implies &boxed{v_{tx{ba}}=v_{tx{bw}}-v_{tx{aw}}}
end{align*}
$$
Using the numbers from the example, we have:
$$
begin{align*}
v_{tx{ba}}=6.5 frac{tx{m}}{tx{s}}-2.5 frac{tx{m}}{tx{s}}=4.0 frac{tx{m}}{tx{s}}
end{align*}
$$
In fact, if we were moving at the same speed of the wind and in the same direction, we should not feel any wind.
—
#### Conclusion
When we sail against the wind our speed relative to the wind is equal to the sum of the speed of the boat plus the speed of the wind, relative to some reference system. When we sail downwind, our speed relative to the wind is equal to the speed of the boat minus the speed of the wind. In the first case we have the sensation of a stronger wind and in the second case of a less strong wind.
a.)125 m/s due east
b.)0 m/s
#### Known
The movement of objects is relative, it depends on the reference system from where it is being studied.
#### Calculation
Givens: $v_{tx{pg}}=16.5 frac{tx{m}}{tx{s}}$, speed of the plane relative to the ground. $v_{tx{ap}}=1.22 frac{tx{m}}{tx{s}}$, speed of the flight attendant relative to the plane.
The flight attendant’s velocity relative to the ground is $vec{v}_{tx{ag}}$, where:
$$
begin{align*}
vec{v}_tx{ag}=(-vec{v}_tx{ap})+vec{v}_tx{pg}=-vec{v}_tx{ap}+vec{v}_tx{pg}
end{align*}
$$
The negative sign is because we have considered the flight attendant’s velocity as negative, in the opposite direction to the velocity of the plane relative to the ground.
$$
begin{align*}
therefore v_tx{ag}&=-v_tx{ap}+v_tx{pg}=-1.22 frac{tx{m}}{tx{s}}+16.5 frac{tx{m}}{tx{s}}\
&=15.28 frac{tx{m}}{tx{s}}
end{align*}
$$
—
#### Conclusion
The flight attendant’s speed with respect to the ground is $15.28 frac{tx{m}}{tx{s}}$.
Graphically:

#### Known
The movement of objects is relative, it depends on the reference system from where it is being studied.
#### Calculation
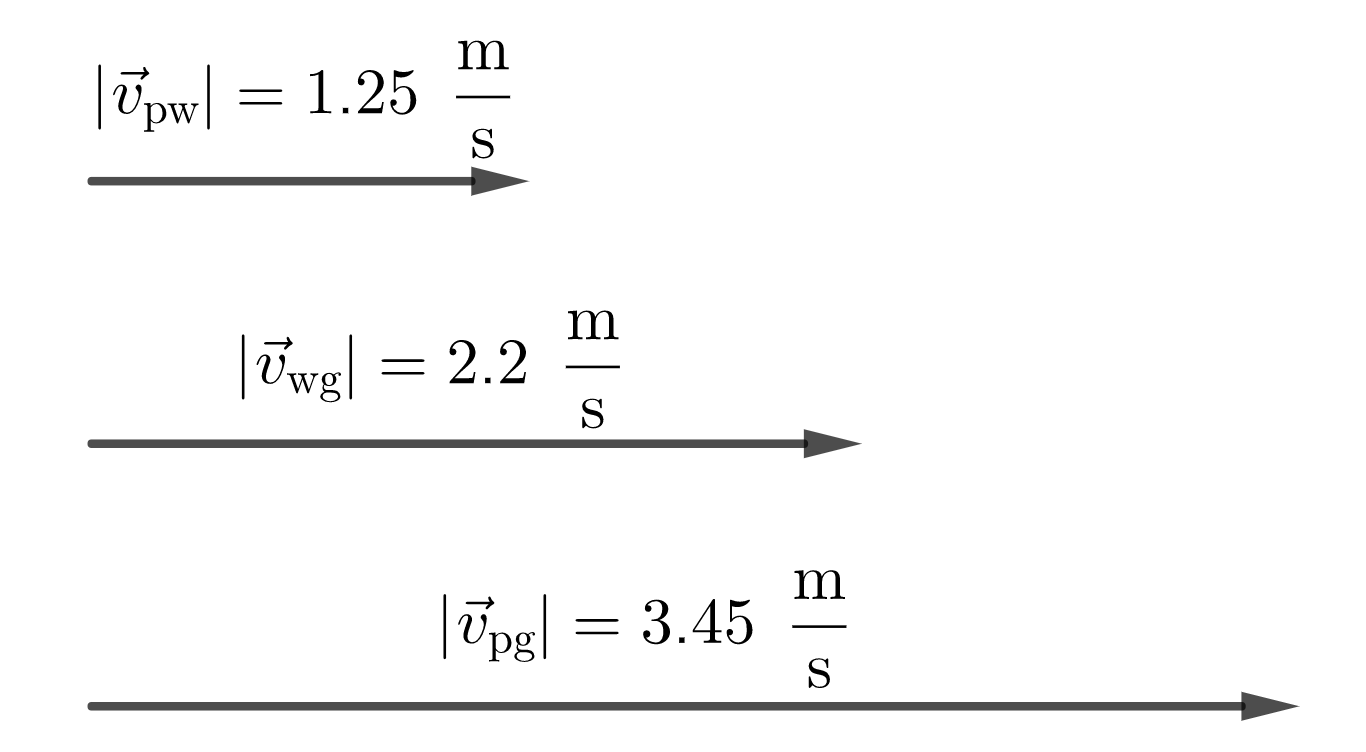
Givens: $v_{tx{wg}}=2.2 frac{tx{m}}{tx{s}}$, speed of the walkway relative to the ground. $d=85 tx{m}$. $t=68 tx{s}$, time it takes us to travel $85 tx{m}$.
Our speed $v_tx{pw}$ with respect to the walkway is:
$$
begin{align*}
v_tx{pw}=frac{d}{t}=frac{85 tx{m}}{68 tx{s}}=1.25 frac{tx{m}}{tx{s}}
end{align*}
$$
Therefore, with respect to the ground, while walking on the walkway, we have a velocity of:
$$
begin{align*}
vec{v}_tx{pg}=vec{v}_tx{pw}+vec{v}_tx{wg}
end{align*}
$$
With $vec{v}_tx{pw}$ and $vec{v}_tx{wg}$ in the same direction.
$$
begin{align*}
therefore v_tx{pg}&=v_tx{pw}+v_tx{wg}=1.25 frac{tx{m}}{tx{s}}+2.2 frac{tx{m}}{tx{s}}\
&=3.45 frac{tx{m}}{tx{s}}
end{align*}
$$
With this speed, traveling the $85 tx{m}$ will takes us a time of:
$$
begin{align*}
t=frac{d}{v_tx{pg}}=frac{85 tx{m}}{3.45 frac{tx{m}}{tx{s}}}=24.6 tx{s}
end{align*}
$$
—
#### Conclusion
$$
begin{align*}
boxed{t=24.6 tx{s}}
end{align*}
$$
Graphically:
begin{align*}
boxed{t=24.6 text{s}}
end{align*}
$$
85/3.45 = 24.637 ~ 25s.
#### Known
The movement of objects is relative, it depends on the reference system from where it is being studied.
#### Calculation
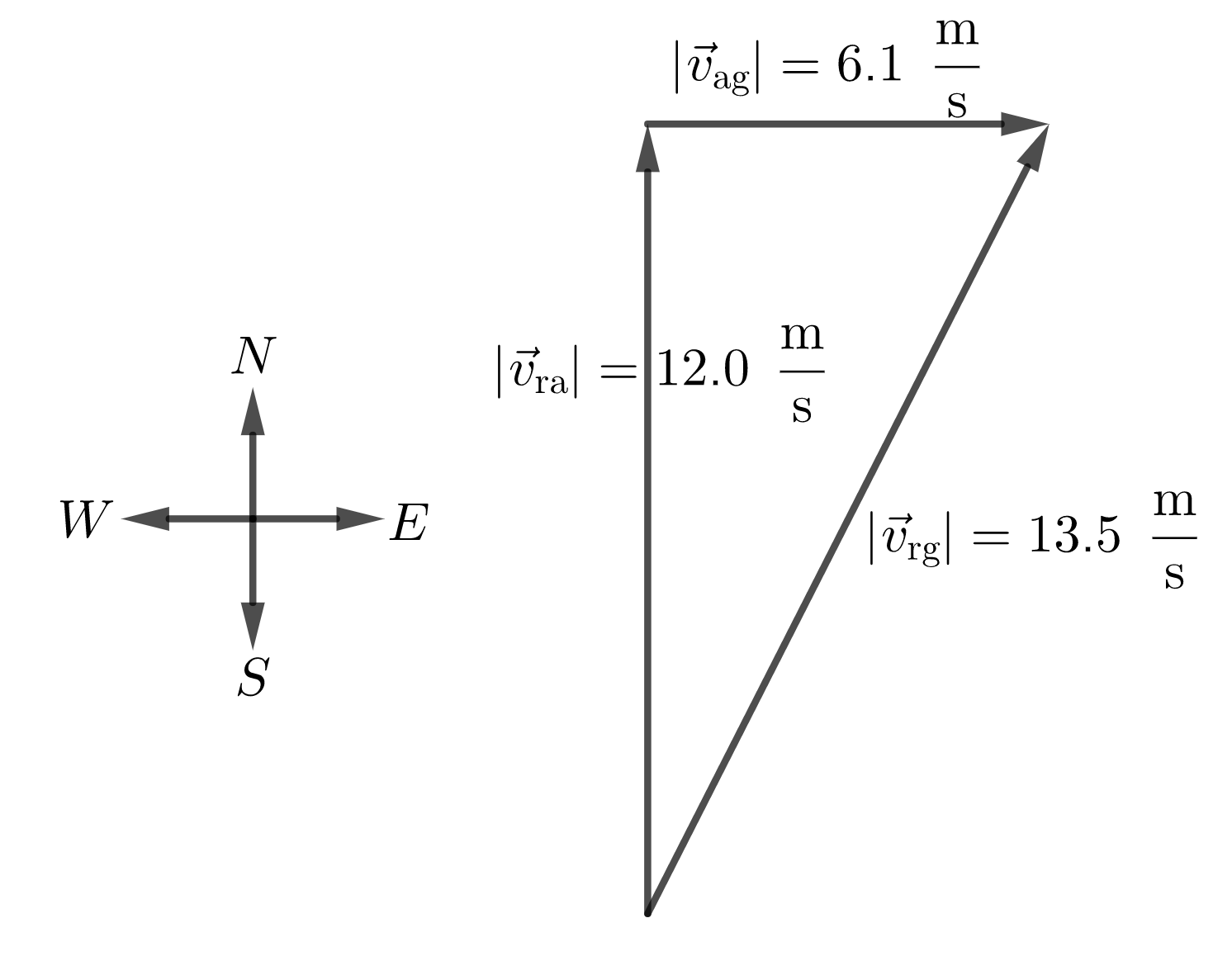
Givens: $v_{tx{ra}}=12 frac{tx{m}}{tx{s}}$, robin’s speed relative to the air. $v_{tx{ag}}=6.1 frac{tx{m}}{tx{s}}$, air speed relative to the ground.
The velocity of the robin with respect to the ground is:
$$
begin{align*}
vec{v}_tx{rg}=vec{v}_tx{ra}+vec{v}_tx{ag}
end{align*}
$$
The robin travels north relative to the air and the air blows east relative to the ground. Therefore the speed of the robin with respect to the ground is:
$$
begin{align*}
v_tx{rg}&=sqrt{(v_tx{ra})^2+(v_tx{ag})^2}=sqrt{left(12 frac{tx{m}}{tx{s}}right)^2+left(6.1 frac{tx{m}}{tx{s}}right)^2}\
&=13.5 frac{tx{m}}{tx{s}}
end{align*}
$$
This is the Pythagorean theorem for right triangles.
—
#### Conclusion
The speed of the robin with respect to the ground is $13.5 frac{tx{m}}{tx{s}}$.
Graphically:
#### Known
The movement of objects is relative, it depends on the reference system from where it is being studied.
#### Calculation
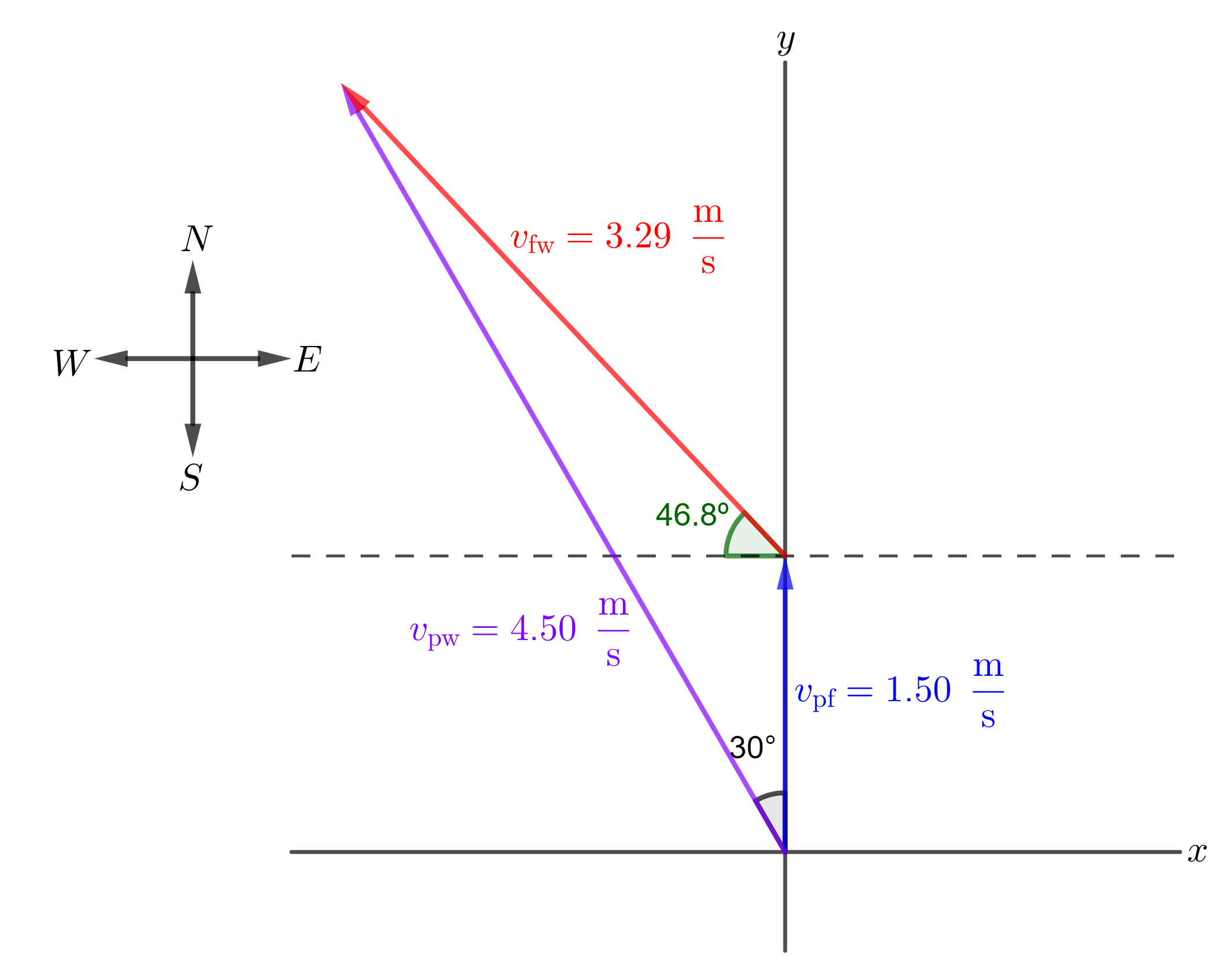
Givens: $v_{tx{pf}}=1.50 frac{tx{m}}{tx{s}}$, passenger speed relative to the ferry. $v_{tx{pw}}=4.50 frac{tx{m}}{tx{s}}$, passenger speed relative to water.
Passenger velocity $vec{v}_tx{pw}$ relative to water is:
$$
begin{align}
vec{v}_tx{pw}=vec{v}_tx{pf}+vec{v}_tx{fw}implies vec{v}_tx{fw}=vec{v}_tx{pw}-vec{v}_tx{pf}
end{align}
$$
Where $vec{v}_tx{fw}$ is the velocity of the ferry with respect to the water.
Passenger velocity $vec{v}_tx{pf}$ relative to the ferry is due north, while relative to the water, $vec{v}_tx{pw}$ points to $30^circ$ west of north.
Using a coordinate system with the positive $y$ axis in the north direction and the positive $x$ axis in the east direction, we have:
$$
begin{align*}
v_{tx{pw}, x}&=v_tx{pw} tx{cos}(theta)=left(-4.50 frac{tx{m}}{tx{s}}right) tx{cos}(90^circ-30^circ)\
&=left(-4.50 frac{tx{m}}{tx{s}}right) tx{sin}(30^circ)\
&=-2.25 frac{tx{m}}{tx{s}}
end{align*}
$$
The negative sign is because we have assumed the westward direction as negative.
Note that we have also used the angle $theta =90^circ-60^circ$, since the angle they give us is with respect to the positive $y$ axis (west of north).
$$
begin{align*}
v_{tx{pw}, y}&=v_tx{pw} tx{sin}(theta)=left(4.50 frac{tx{m}}{tx{s}}right) tx{sin}(90^circ-30^circ)\
&=left(4.50 frac{tx{m}}{tx{s}}right) tx{cos}(30^circ)\
&=3.897 frac{tx{m}}{tx{s}}approx 3.90 frac{tx{m}}{tx{s}}
end{align*}
$$
Regarding the ferry we have:
$$
begin{align*}
v_{tx{pf}, x}=0 frac{tx{m}}{tx{s}}hspace{0.5cm}tx{and}hspace{0.5cm} v_{tx{pf}, y}=1.50 frac{tx{m}}{tx{s}}
end{align*}
$$
Therefore from (1), we have:
$$
begin{align*}
v_{tx{fw}, x}&=v_{tx{pw}, x}-v_{tx{pf}, x}=-2.25 frac{tx{m}}{tx{s}}-0 frac{tx{m}}{tx{s}}\
&=-2.25 frac{tx{m}}{tx{s}}\
v_{tx{fw}, y}&=v_{tx{pw}, y}-v_{tx{pf}, y}=3.90 frac{tx{m}}{tx{s}}-1.50 frac{tx{m}}{tx{s}}\
&=2.40 frac{tx{m}}{tx{s}}\
implies vec{v}_tx{fw}&=(v_{tx{fw}, x}, v_{tx{fw}, y})=left(-2.25 frac{tx{m}}{tx{s}}, 2.40 frac{tx{m}}{tx{s}}right)\
implies v_tx{fw}&=sqrt{left(-2.25 frac{tx{m}}{tx{s}}right)^2+left(2.40 frac{tx{m}}{tx{s}}right)^2}\
&=3.29 frac{tx{m}}{tx{s}}\
theta&=tx{tan}^{-1}left(frac{v_{tx{fw}, y}}{v_{tx{fw}, x}}right)=tx{tan}^{-1}left(frac{2.40 cancel{frac{tx{m}}{tx{s}}}}{-2.25 cancel{frac{tx{m}}{tx{s}}}}right)\
&=133.2^circ tx{with respect to the positive} x tx{axis}.
end{align*}
$$
With respect to the north the direction is:
$$
begin{align*}
theta_tx{N}=133.2^circ-90^circ=43.2^circ tx{west of north}.
end{align*}
$$
Or with respect to the west:
$$
begin{align*}
theta_tx{W}=180^circ-133.2^circ=tx{tan}^{-1}left(frac{2.40 cancel{frac{tx{m}}{tx{s}}}}{2.25 cancel{frac{tx{m}}{tx{s}}}}right)=46.8^circ tx{north of west}.
end{align*}
$$
—
#### Conclusion
The velocity of the ferry with respect to the water has a magnitude of $3.29 frac{tx{m}}{tx{s}}$ and points in a direction of $46.8^circ$ north of west.
Graphically:
subsection*{Known}
If an object is moving with a velocity $vec{v}_{12}$ with respect to an object 2 and this object 2 is moving with a velocity $vec{v}_{23}$ with respect to an object 3, then the velocity of object 1 with respect to object 3 is given by:
begin{align*}
vec{v}_{13}=vec{v}_{12}+vec{v}_{23}
end{align*}
subsection*{Calculation}
Givens: $v_{ag}=36 frac{tx{km}}{tx{h}}$, air speed relative to the ground. $v_{pa}=350 frac{tx{km}}{tx{h}}$, speed of the pilot relative to the ground.\
a) The pilot wants to fly north ($vec{v}_{pg}$) while the wind is blowing west ($vec{v}_{ag}$). Therefore, taking into account that these two speeds are perpendicular ($vec{v}_{pg}perpvec{v}_{ag}$), the direction of the plane with respect to the air is (see Figure part b):
begin{align}
theta&=tx{sin}^{-1}left(frac{tx{opposite side}}{tx{hypotenuse}}right)notag\
&=tx{sin}^{-1}left(frac{v_{ag}}{v_{pa}}right)=tx{sin}^{-1}left(frac{36 cancel{frac{tx{km}}{tx{h}}}}{350 cancel{frac{tx{km}}{tx{h}}}}right)\
&=5.9^circ tx{east of north}notag
end{align}
b)
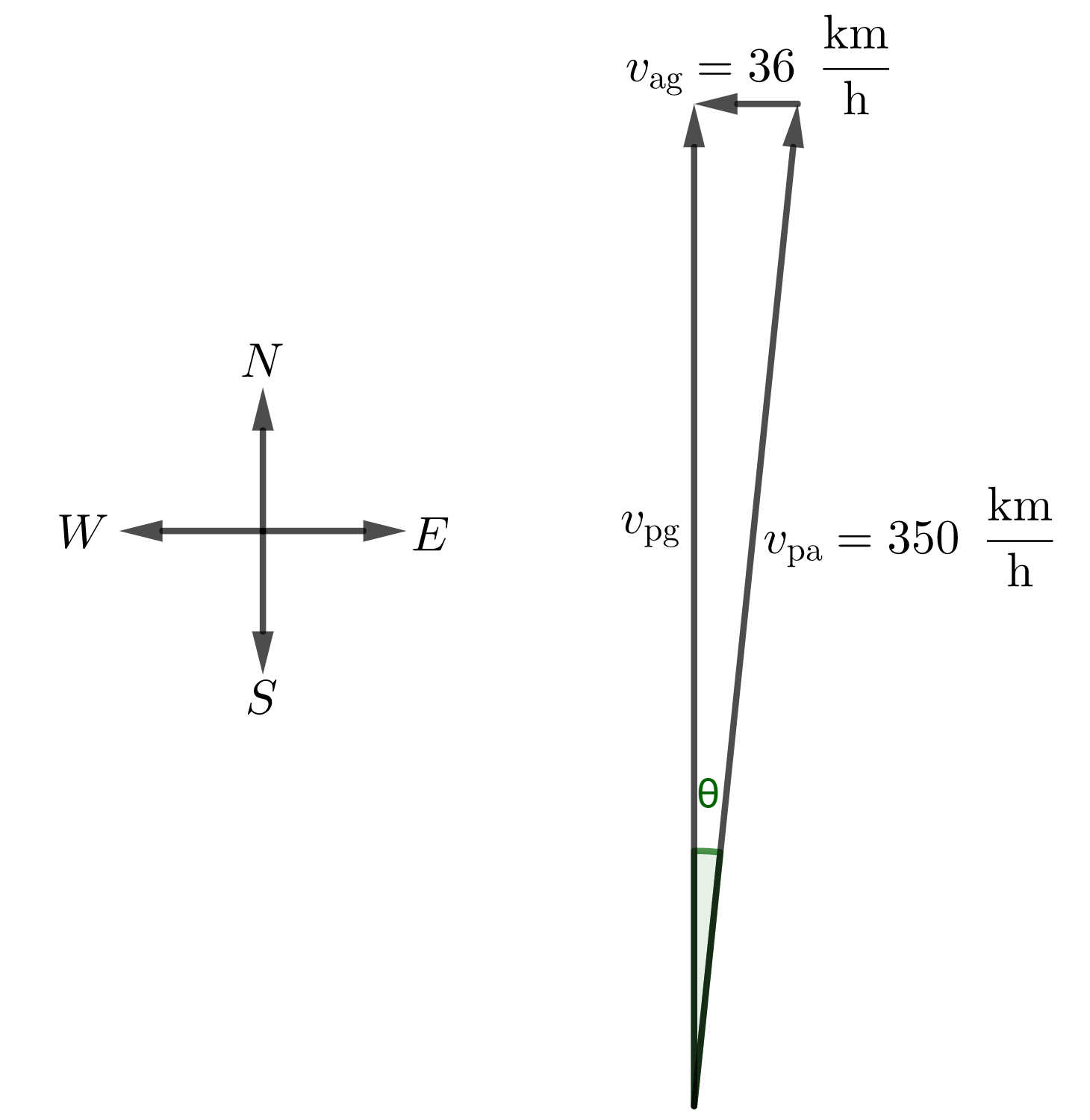
—
#### Conclusion
a) $theta=5.9^circ$ east of north.
c) The pilot should increase the angle relative to the east of north.
c) The pilot should increase the angle relative to the east of north.
#### Known
If an object is moving with a velocity $vec{v}_{12}$ with respect to an object 2 and this object 2 is moving with a velocity $vec{v}_{23}$ with respect to an object 3, then the velocity of object 1 with respect to object 3 is given by:
$$
begin{align*}
vec{v}_{13}=vec{v}_{12}+vec{v}_{23}
end{align*}
$$
#### Calculation
Givens: $v_{rg}=2.8 frac{tx{m}}{tx{s}}$, river relative to the ground. $v_{jg}=9.5 frac{tx{m}}{tx{s}}$, jet ski relative to the ground.
The direction of the jet ski relative to the river is $35^circ$ and relative to the ground is $20^circ$. Thus:
$$
begin{align}
vec{v}_tx{jg}=vec{v}_tx{jr}+vec{v}_tx{rg}implies vec{v}_tx{jr}=vec{v}_tx{jg}-vec{v}_tx{rg}
end{align}
$$
Where $vec{v}_tx{jr}$ is the velocity of the jet ski relative to the river.
Therefore, from (1) we have:
$$
begin{align*}
v_{tx{jr}, x}&=v_{tx{jg}, x}-v_{tx{rg}, x}=left(9.5 frac{tx{m}}{tx{s}}right) tx{cos}(20^circ)-0 frac{tx{m}}{tx{s}}\
&=8.93 frac{tx{m}}{tx{s}}approx 8.9 frac{tx{m}}{tx{s}}\
v_{tx{jr}, y}&=v_{tx{jg}, y}-v_{tx{rg}, y}=left(9.5 frac{tx{m}}{tx{s}}right) tx{sin}(20^circ)-left(-2.8 frac{tx{m}}{tx{s}}right)\
&=6.05 frac{tx{m}}{tx{s}}approx 6.1 frac{tx{m}}{tx{s}}
end{align*}
$$
The negative sign of $v_tx{rg}$ is due to the fact that we have chosen the downstream direction as negative.
Hence:
$$
begin{align*}
vec{v}_tx{jr}&=(v_{tx{jr}, x}, v_{tx{jr}, y})=left(8.9 frac{tx{m}}{tx{s}}, 6.1 frac{tx{m}}{tx{s}}right)\
implies v_tx{jr}&=sqrt{(v_{tx{jr}, x})^2+(v_{tx{jr}, y})^2}=sqrt{left(8.9 frac{tx{m}}{tx{s}}right)^2+left(6.1 frac{tx{m}}{tx{s}}right)^2}\
&=10.79 frac{tx{m}}{tx{s}}approx 10.8 frac{tx{m}}{tx{s}}
end{align*}
$$
—
#### Conclusion
The speed of the jet ski relative to the river is $10.8 frac{tx{m}}{tx{s}}$.
Graphically:
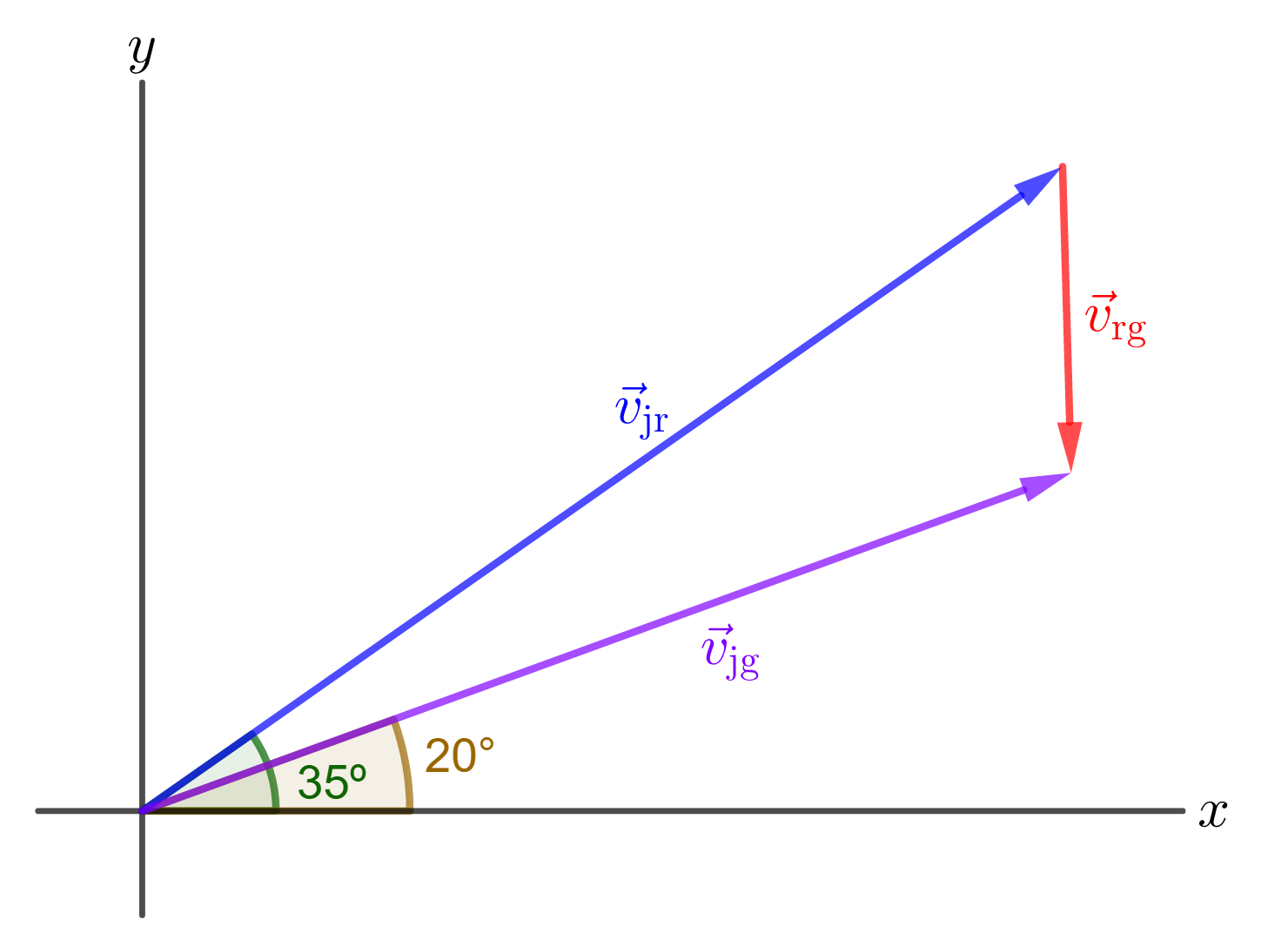
#### Known
Neglecting air resistance, a projectile will move is such a way that its horizontal and vertical motions are independent.
#### Calculation
Givens: $v_{x,i}=5 frac{tx{m}}{tx{s}}$ (horizontal) $v_{y,i}=6 frac{tx{m}}{tx{s}}$ (vertical)
At the highest point we have:
a)
$$
begin{align*}
v_{x,f}=v_{x,i}=5 frac{tx{m}}{tx{s}}
end{align*}
$$
In fact, during the entire trajectory of the projectile, the horizontal component of the initial velocity will not change.
b)
$$
begin{align*}
v_{y,f}=0 frac{tx{m}}{tx{s}}
end{align*}
$$
At the highest point the vertical component of velocity changes direction, from upward to downward. So at this point the vertical component of velocity has to be zero.
—
#### Conclusion
$$
begin{align*}
tx{a}) boxed{v_x=5 frac{tx{m}}{tx{s}} (tx{horizontal})}hspace{0.8cm}tx{b}) boxed{v_y=0 frac{tx{m}}{tx{s}} (tx{vertical})}
end{align*}
$$
begin{align*}
text{a}) boxed{v_x=5 frac{text{m}}{text{s}} (text{horizontal})}hspace{0.8cm}text{b}) boxed{v_y=0 frac{text{m}}{text{s}} (text{vertical})}
end{align*}
$$
#### Known
Neglecting air resistance, a projectile will move is such a way that its horizontal and vertical motions are independent.
a) The horizontal component of velocity of the scoop of ice cream as it falls is the same as the pony’s constant velocity. Therefore the child will observe how the ice cream falls next to him until it reaches the ground. This is because for the child, the ice cream does not have a horizontal component of velocity, since both move at the same horizontal velocity, that is, for the child the ball falls vertically.
b) For parents the ball will have a vertical component of velocity and a horizontal component (unlike the child). Therefore they will observe that the ball falls following a parabolic trajectory (only part of the parabola).
—
#### Conclusion
a) For the boy, the ice cream scoop falls vertically.
b) For parents, the ice cream scoop falls following a parabolic trajectory (only part of the parabola).
b) For parents, the ice cream scoop falls following a parabolic trajectory (only part of the parabola).
#### Known
The acceleration of gravity can be considered constant at all points near the surface of the earth and in a downward direction (radial direction towards the center of the earth). Therefore, neglecting air resistance, the acceleration of a projectile is equal to the acceleration of gravity at all times in its trajectory. This is:
$$
begin{align*}
a_y=g=9.81 frac{tx{m}}{tx{s}^2}, tx{in the “downward” direction}.
end{align*}
$$
—
#### Conclusion
At each point on its trajectory, a projectile moves with the same acceleration:
$$
begin{align*}
a_y=g=9.81 frac{tx{m}}{tx{s}^2}, tx{in the “downward” direction}.
end{align*}
$$
begin{align*}
a_y=g=9.81 frac{text{m}}{text{s}^2}, text{in the “downward” direction}.
end{align*}
$$
#### Known
Neglecting air resistance, a projectile will move is such a way that its horizontal and vertical motions are independent.
The maximum height of a projectile depends basically on the vertical component of the initial velocity (also on the acceleration of gravity if we are not on Earth). The higher the vertical component of the initial velocity, the longer the projectile will be in the air (flight time) and will reach a higher altitude.
The vertical component of velocity is given by:
$$
begin{align}
v_{y,i}=v_i tx{sin}(theta)implies boxed{v_i=frac{v_{y,i}}{tx{sin}(theta)}}
end{align}
$$
The above relationship implies that for a given vertical component of velocity, the greater the launch angle $theta$ with respect to the horizontal, the initial velocity $v_i$ will be lower.
Therefore:
a) The maximum height of the three projectiles is the same, so their initial velocity vertical components are also the same. This implies that projectile A has the lowest initial velocity $v_i$ (highest $theta$), it is followed by projectile B and the highest initial velocity would be for projectile C (lowest $theta$). See expression (1).
b) The flight time is the same for the three projectiles, since the maximum height is the same in all three cases, that is, they will be in the air for the same time regardless of their horizontal components of velocity. This can be easily seen using the time of flight expression.
$$
begin{align}
t_v=frac{2v_{y,i}}{g}=frac{2v_i tx{sin}(theta)}{g}
end{align}
$$
With $v_{y,i}=v_i tx{sin}(theta)$ equal for the three projectiles, see part a).
The result of part a) can also be derived from the equation of the range:
$$
begin{align*}
R=left(frac{v_i^2}{g}right) tx{sin}(2theta)
end{align*}
$$
From the Figure 4.36 it can be seen that projectile C has the highest range with the smallest launch angle theta, therefore its initial velocity will be the highest, while that of projectile A will be the lowest.
—
#### Conclusion
$$
begin{align*}
tx{a}) boxed{tx{A}<tx{B}<tx{C}}hspace{0.5cm}tx{b}) boxed{tx{A}=tx{B}=tx{C}}
end{align*}
$$
begin{align*}
text{a}) boxed{text{A}<text{B}<text{C}}hspace{0.5cm}text{b}) boxed{text{A}=text{B}=text{C}}
end{align*}
$$
#### Known
Neglecting air resistance, a projectile will move is such a way that its horizontal and vertical motions are independent.
Therefore while the vertical component of velocity changes with time or height, the horizontal component remains constant $(v_{x,f}=v_{x,i}=v_i)$. At maximum height, the vertical component of velocity is zero ($v_{y,f}=0$).
#### Calculation
Givens: $v_i=12 frac{tx{m}}{tx{s}}$, $v=6 frac{tx{m}}{tx{s}}$ at the highest point.
At the highest point:
$$
begin{align*}
v_{y,f}=0 frac{tx{m}}{tx{s}}implies v=v_{x,f}=v_{x,i}, tx{since} vec{v}=(v_x, v_y)
end{align*}
$$
Therefore:
$$
begin{align*}
&v_{x,i}=v_i tx{cos}(theta)=v\
&implies tx{cos}(theta)=frac{v}{v_i}\
&implies theta=tx{cos}^{-1}left(frac{v}{v_i}right)=tx{cos}^{-1}left(frac{6 cancel{frac{tx{m}}{tx{s}}}}{12 cancel{frac{tx{m}}{tx{s}}}}right)=tx{cos}^{-1}left(frac{1}{2}right)\
&thereforeboxed{theta=60^circ}
end{align*}
$$
—
#### Conclusion
$$
begin{align*}
boxed{theta=60^circ}
end{align*}
$$
begin{align*}
boxed{theta=60^circ}
end{align*}
$$
begin{align}
y_f&=y_i+v_{y,i}t-frac{1}{2}gt^2 \
x_f&=x_i+v_{x,i}t
end{align}
tt{we know that the initial velocity of the ball $v_i$ was purely horizontal thefore $v_{y,i}=0$, additionally we will take the origin of motion as the origin of the horizontal axis meaning $x_i=0$, consequentially: }
setcounter{equation}{0}
begin{align}
y_f&=y_i-frac{1}{2}gt^2 \
x_f&=v_{x,i}t
end{align}
At the moment of impact, we will solve the x-equation for $t$:
begin{align*}
t&=frac{x_f}{v_{x,i}}\
&=frac{(1.95m)}{(4.87frac{m}{s})}\
&=boxed{0.4s}
end{align*}
At the moment of impact,we know that the ball hit the court therefore $y_f=0$, we will solve the y-equation for $y_i$:
begin{align*}
y_i&=frac{1}{2}gt^2\
&=frac{1}{2}(9.81frac{m}{s^2})(0.4s)^2\
&=boxed{textcolor{blue}{0.78m}}
end{align*}
tt{$y_i=0.78m$}
$$
#### Known
Neglecting air resistance, a projectile will move is such a way that its horizontal and vertical motions are independent.
The horizontal and vertical positions of a projectile are determined by:
$$
begin{align}
&x_f=x_i+v_{x,i}cdot t\
&y_f=y_i+v_{y,i}cdot t-frac{gcdot t^2}{2}
end{align}
$$
#### Calculation
Givens: $v_{x,i}=4.87 frac{tx{m}}{tx{s}}$, $v_{y,i}=0 frac{tx{m}}{tx{s}}$, $x_i=0 tx{m}$, $x_f=1.95 tx{m}$, $y_f=0 tx{m}$, $g=9.81 frac{tx{m}}{tx{s}^2}$.
From (1) we have:
$$
begin{align*}
&t=frac{x_f-x_i}{v_{x,i}}=frac{1.95 tx{m}-0 tx{m}}{4.87 frac{tx{m}}{tx{s}}}\
&boxed{t=0.40 tx{s}}
end{align*}
$$
Substituting this time in equation (2), we have:
$$
begin{align*}
0 tx{m}=&y_i+left(0 frac{tx{m}}{tx{s}}right)(0.40 tx{s})-frac{left(9.81 frac{tx{m}}{tx{s}^2}right)(0.40 tx{s})^2}{2}\
implies &y_i=frac{left(9.81 frac{tx{m}}{tx{s}^2}right)(0.40 tx{s})^2}{2}\
&boxed{y_i=0.78 tx{m}}
end{align*}
$$
—
#### Conclusion
The racket ball was at a height of $0.78 tx{m}$ from the court.
#### Known
The water from the waterfall falls like a projectile. The horizontal and vertical components of velocity are given by:
$$
begin{align*}
&v_{x,f}=v_{x,i}\
&v_{y,f}=v_{y,i}-gcdot t\
&v_{y,f}^2=v_{y,i}^2-2g(y_f-y_i)
end{align*}
$$
#### Calculation
Givens: $y_i=108 tx{m}$, $y_f=0 tx{m}$, $g=9.81 frac{tx{m}}{tx{s}^2}$, $v_{x,i}=3.60 frac{tx{m}}{tx{s}}$, $v_{y,i}=0 frac{tx{m}}{tx{s}}$.
When the water reaches the bottom, its velocity is given by:
$$
begin{align*}
vec{v}=(v_{x,f}, v_{y,f})implies v=sqrt{(v_{x,f})^2+(v_{y,f})^2}
end{align*}
$$
With:
$$
begin{align*}
boxed{v_{x,f}=v_{x,i}=3.60 frac{tx{m}}{tx{s}}}
end{align*}
$$
$$
begin{align*}
v_{y,f}^2&=left(0 frac{tx{m}}{tx{s}}right)^2-2left(9.81 frac{tx{m}}{tx{s}^2}right)(0 tx{m}-108 tx{m})\
&=2118.96 frac{tx{m}^2}{tx{s}^2}\
implies v_{y,f}&=-46.03 frac{tx{m}}{tx{s}}
end{align*}
$$
The negative sign is because it is in the downward direction (assumed to be negative).
$$
begin{align*}
therefore v&=sqrt{left(3.60 frac{tx{m}}{tx{s}}right)^2+left(-46.03 frac{tx{m}}{tx{s}}right)^2}\
&=46.17 frac{tx{m}}{tx{s}}
end{align*}
$$
—
#### Conclusion
The speed of the water hitting the bottom is $46.17 frac{tx{m}}{tx{s}}$.
#### Known
Neglecting air resistance, a projectile will move is such a way that its horizontal and vertical motions are independent.
Considering the ball as a projectile, its horizontal and vertical movement is determined by the equations:
$$
begin{align}
&x_f=x_i+v_{x,i}cdot t\
&y_f=y_i+v_{y,i}cdot t-frac{gcdot t^2}{2}
end{align}
$$
#### Calculation
Givens: $v_{x,i}=22 frac{tx{m}}{tx{s}}$, $v_{y,i}=0 frac{tx{m}}{tx{s}}$, $t=0.45 tx{s}$ $x_i=0 tx{m}$, $y_f=0 tx{m}$, $g=9.81 frac{tx{m}}{tx{s}^2}$.
a) The horizontal component of velocity does not change, therefore, from expression (1) we have:
$$
begin{align*}
d_x&=|x_f-x_i|=|v_{x,i}cdot t|\
&=big|left(22 frac{tx{m}}{tx{s}}right)(0.45 tx{s})big|\
&=9.90 tx{m}
end{align*}
$$
b) From (2) we have:
$$
begin{align*}
d_y&=|y_f-y_i|=big|v_{y,i}cdot t-frac{gcdot t^2}{2}big|\
&=big|left(0 frac{tx{m}}{tx{s}}right)(0.45 tx{s})-frac{left(9.81 frac{tx{m}}{tx{s}^2}right)(0.45 tx{s})^2}{2}big|\
&=|-0.99 tx{m}|=0.99 tx{m}
end{align*}
$$
We have taken the absolute value or modulus in the equations, since the distance between two points is positive definite, it is always greater than or equal to zero. A negative distance is meaningless, as does a negative mass or negative time.
Note: This is not true in a Minkowski space.
—
#### Conclusion
$$
begin{align*}
&tx{a}) d_x=9.90 tx{m}\
&tx{b}) d_y=0.99 tx{m}
end{align*}
$$
begin{align*}
&text{a}) d_x=9.90 text{m}\
&text{b}) d_y=0.99 text{m}
end{align*}
$$
#### Known
Neglecting air resistance, a projectile will move is such a way that its horizontal and vertical motions are independent.
The clam in its free fall moves like a projectile. The horizontal and vertical components of velocity are given by:
$$
begin{align}
&v_{x,f}=v_{x,i}\
&v_{y,f}=v_{y,i}-gcdot t
end{align}
$$
#### Calculation
Givens: $v_{x,i}=2.70 frac{tx{m}}{tx{s}}$, $v_{y,i}=0 frac{tx{m}}{tx{s}}$, $t=2.10 tx{s}$, $g=9.81 frac{tx{m}}{tx{s}^2}$
a)
$$
begin{align*}
v_{x,f}=v_{x,i}=2.70 frac{tx{m}}{tx{s}}
end{align*}
$$
The horizontal component of velocity does not change.
b) From (2) we have:
$$
begin{align*}
v_{y,f}&=left(0 frac{tx{m}}{tx{s}}right)-left(9.81 frac{tx{m}}{tx{s}^2}right)(2.10 tx{s})\
&=-20.60 frac{tx{m}}{tx{s}}
end{align*}
$$
The negative sign is because we have chosen downward as the negative direction.
—
#### Conclusion
$$
begin{align*}
tx{a}) boxed{v_{x,f}=2.70 frac{tx{m}}{tx{s}}}hspace{0.5cm} tx{b}) boxed{v_{y,f}=-20.60 frac{tx{m}}{tx{s}}}
end{align*}
$$
begin{align*}
text{a}) boxed{v_{x,f}=2.70 frac{text{m}}{text{s}}}hspace{0.5cm} text{b}) boxed{v_{y,f}=-20.60 frac{text{m}}{text{s}}}
end{align*}
$$
B. v = a t = 9.8 * 2.1= 20.58 m/s
#### Known
Neglecting air resistance, a projectile will move is such a way that its horizontal and vertical motions are independent.
The horizontally thrown pumpkin will move like a projectile. The horizontal and vertical components of velocity are given by:
$$
begin{align*}
&v_{x,f}=v_{x,i}\
&v_{y,f}=v_{y,i}-gcdot t
end{align*}
$$
The horizontal and vertical positions are given by:
$$
begin{align}
&x_f=x_i+v_{x,i}cdot t\
&y_f=y_i+v_{y,i}cdot t-frac{gcdot t^2}{2}
end{align}
$$
#### Calculation
Givens: $x_i=0 tx{m}$, $y_i=9 tx{m}$, $x_f=3.5 tx{m}$, $y_f=0 tx{m}$, $g=9.81 frac{tx{m}}{tx{s}^2}$.
The vertical component of the initial velocity is zero. Therefore the initial velocity has only a horizontal component.
$$
begin{align*}
vec{v}_i=(v_{x,i}, v_{y,i})=(v_{x,i}, 0)\
implies v_i=sqrt{(v_{x,i})^2+(v_{y,i})^2}=v_{x,i}
end{align*}
$$
Therefore, from (1) we have:
$$
begin{align}
v_{x,i}=frac{x_f-x_i}{t}
end{align}
$$
We can calculate the time using equation (2), this is:
$$
begin{align*}
&0 tx{m}=9 tx{m}+left(0 frac{tx{m}}{tx{s}}right)t-frac{left(9.81 frac{tx{m}}{tx{s}^2}right)t^2}{2}\
&implies t=sqrt{frac{2(-9 tx{m})}{-9.81 frac{tx{m}}{tx{s}^2}}}=1.355 tx{s}
end{align*}
$$
Substituting this time in equation (3), we have:
$$
begin{align*}
v_{x,i}=frac{3.5 tx{m}-0 tx{m}}{1.355 tx{s}}=2.58 frac{tx{m}}{tx{s}}
end{align*}
$$
Therefore:
$$
begin{align*}
v_i=v_{x,i}=2.58 frac{tx{m}}{tx{s}}
end{align*}
$$
—
#### Conclusion
The pumpkin has to be thrown with a speed of $2.58 frac{tx{m}}{tx{s}}$.
#### Known
The range of a projectile is determined by its initial velocity $v_i$, the launch angle $theta$, and by the acceleration of gravity $g$. This range is maximum when the launch angle is $45^circ$, as long as the projectile falls to the same horizontal level from where it started. This is:
$$
begin{align}
R_{tx{max}}=frac{v_i^2}{g}
end{align}
$$
#### Calculation
Givens: $R_{tx{max}}=1245 tx{m}$, $g=9.81 frac{tx{m}}{tx{s}^2}$
From (1) we have:
$$
begin{align*}
v_i&=sqrt{gcdot R_{tx{max}}}=sqrt{left(9.81 frac{tx{m}}{tx{s}^2}right)(1245 tx{m})}\
&=110.5 frac{tx{m}}{tx{s}}approx 111 frac{tx{m}}{tx{s}}
end{align*}
$$
—
#### Conclusion
A minimum initial speed of $111 frac{tx{m}}{tx{s}}$ is required.
#### Known
Neglecting air resistance, a projectile will move is such a way that its horizontal and vertical motions are independent.
The horizontal and vertical position ($x$, $y$ position) of a projectile are given by the equations:
$$
begin{align}
&x_f=x_i+v_{x,i}cdot t\
&y_f=y_i+v_{y,i}cdot t-frac{gcdot t^2}{2}
end{align}
$$
#### Calculation
Givens: $x_i=0 tx{m}$, $y_i=3.0 tx{m}$, $v_{x,i}=1.8 frac{tx{m}}{tx{s}}$, $v_{y,i}=0 frac{tx{m}}{tx{s}}$, $g=9.81 frac{tx{m}}{tx{s}^2}$
a) At $t=0.25 tx{s}$, using (1):
$$
begin{align*}
x&=0 tx{m}+left(1.8 frac{tx{m}}{tx{s}}right)(0.25 tx{s})\
&=0.45 tx{m}\
y&=3.0 tx{m}+left(0 frac{tx{m}}{tx{s}}right)(0.25 tx{s})-frac{left(9.81 frac{tx{m}}{tx{s}^2}right)(0.25 tx{s})^2}{2}\
&=2.69 tx{m}
end{align*}
$$
At $t=0.50 tx{s}$, using (1):
$$
begin{align*}
x&=0 tx{m}+left(1.8 frac{tx{m}}{tx{s}}right)(0.50 tx{s})\
&=0.90 tx{m}\
y&=3.0 tx{m}+left(0 frac{tx{m}}{tx{s}}right)(0.50 tx{s})-frac{left(9.81 frac{tx{m}}{tx{s}^2}right)(0.50 tx{s})^2}{2}\
&=1.77 tx{m}
end{align*}
$$
At $t=0.75 tx{s}$, using (1):
$$
begin{align*}
x&=0 tx{m}+left(1.8 frac{tx{m}}{tx{s}}right)(0.75 tx{s})\
&=1.35 tx{m}\
y&=3.0 tx{m}+left(0 frac{tx{m}}{tx{s}}right)(0.75 tx{s})-frac{left(9.81 frac{tx{m}}{tx{s}^2}right)(0.75 tx{s})^2}{2}\
&=0.24 tx{m}
end{align*}
$$
b) The figure shows the parabolic path followed by the diver.
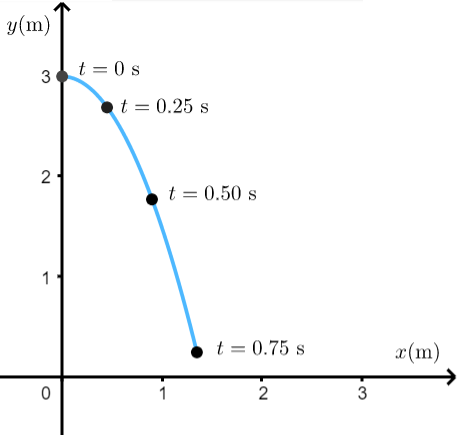
—
#### Conclusion
a) At $t=0.25 tx{s}$, $x=0.45 tx{m}$ and $y=2.69 tx{m}$.
At $t=0.50 tx{s}$, $x=0.90 tx{m}$ and $y=1.77 tx{m}$
At $t=0.75 tx{s}$, $x=1.35 tx{m}$ and $y=0.24 tx{m}$.
At $t=0.50 text{s}$, $x=0.90 text{m}$ and $y=1.77 text{m}$
At $t=0.75 text{s}$, $x=1.35 text{m}$ and $y=0.24 text{m}$.
The distance covered is $d = 2pi r$, and the time taken is $T = 32.0~mathrm{s}$. The speed $v$ must be
$$
begin{align*}
v &= frac{d}{t} \
&= frac{2pi left( 5.00~mathrm{m} right)}{32.0~mathrm{s}} \
&= 0.98174~mathrm{m/s} \
v &= boxed{ 0.982~mathrm{m/s} }
end{align*}
$$
First, we find the time of the trajectory. Notice that the vertical displacement is $y = 1.75~mathrm{m} + 2 left( 5.00~mathrm{m} right) = 11.75~mathrm{m}$. Object is just free-falling, so the time taken for the toy to reach the ground is
$$
begin{align*}
y &= frac{1}{2}gt^{2} \
t &= sqrt{frac{2y}{g}} tag{1}
end{align*}
$$
$$
begin{align*}
d &= v_{x}t \
&= left( frac{2pi r}{T} right) left( sqrt{frac{2y}{g}} right) \
&= left( frac{2pi left( 5.00~mathrm{m} right)}{32.0~mathrm{s}} right) sqrt{frac{2 left( 11.75~mathrm{m} right)}{9.81~mathrm{s}}} \
&= 1.51950~mathrm{m} \
d &= boxed{ 1.52~mathrm{m} }
end{align*}
$$
item [(a)] $v = 0.982~mathrm{m/s}$
item [(b)] $d = 1.52~mathrm{m}$
end{enumerate}
#### Known
The range of a projectile is determined by its initial velocity $v_i$, the launch angle $theta$, and by the acceleration of gravity $g$. This range is maximum when the launch angle is $45^circ$, as long as the projectile falls to the same horizontal level from where it started. This is:
$$
begin{align}
R_{tx{max}}=frac{v_i^2}{g}
end{align}
$$
#### Calculation
Givens: $v_i=34.4 frac{tx{m}}{tx{s}}$, $g=9.81 frac{tx{m}}{tx{s}^2}$
a) From (1) we have:
$$
begin{align*}
R_{tx{max}}=frac{left(34.4 frac{tx{m}}{tx{s}}right)^2}{9.81 frac{tx{m}}{tx{s}^2}}=120.6 tx{m}
end{align*}
$$
b) The velocity $vec{v}$ of the ball at each point of its trajectory is determined by its component on the x-axis and by its component on the y-axis at each of these points. Therefore, its speed $v$ is given by:
$$
begin{align}
vec{v}=(v_x, v_y)implies v=sqrt{v_x^2+v_y^2}
end{align}
$$
The $x$ component of the velocity of the projectile $v_x$ does not change during its flight, therefore, from expression (2) we can see that the velocity of the projectile has its minimum value when its vertical component ($y$ component) of the velocity $v_y$ becomes zero at the point of maximum height.
$$
begin{align*}
vec{v}_{tx{min}}=(v_x, 0)implies v_{tx{min}}=v_x, tx{at maximum height}.
end{align*}
$$
With:
$$
begin{align}
v_x=v_{x,i}=v_i tx{cos}(theta)
end{align}
$$
Where $theta=45^circ$, the angle for the maximum range.
Finally from (3) we have:
$$
begin{align*}
v_{tx{min}}&=v_x=left(34.4 frac{tx{m}}{tx{s}}right) tx{cos}(45^circ)\
&=24.3 frac{tx{m}}{tx{s}}
end{align*}
$$
—
#### Conclusion
$$
begin{align*}
tx{a}) boxed{R_{tx{max}}=120.6 tx{m}} hspace{0.5cm} tx{b}) boxed{v_{tx{min}}=24.3 frac{tx{m}}{tx{s}}}
end{align*}
$$
begin{align*}
text{a}) boxed{R_{text{max}}=120.6 text{m}} hspace{0.5cm} text{b}) boxed{v_{text{min}}=24.3 frac{text{m}}{text{s}}}
end{align*}
$$
at the highest point, the vertical velocity is zero; therefore, we can figure out the initial vertical velocity by knowing gravity decreases the speed of a rising object by 9.8m/s for each second of flight
therefore, if it took 2.25 s for the object’s vertical velocity to reach 0, its initial vertical velocity was 9.8m/s/s x 2.25 s = 22.05m/s
finally, the initial vertical velocity is v0sin63 where v0 is the total initial velocity
we know that v0sin 63=22.05
so v0=22.05/sin63=24.77 m/s
a) No, unless the high fly ball went straight up 90 degrees, because otherwise, the ball is always accelerating towards the ground, which is straight down. So normally, the ball will not reach a point during flight where it’s velocity is parallel to it’s acceleration.
throughout the flight the force acting on boding is only gravity so the acceleration of both bodies is same tough they reach ground at different times
#### Known
The movement of a projectile is symmetric, that is, knowing only the movement of the projectile up to its maximum height, we can describe its movement of fall from this point, to the level from where it was launched (and vice versa). For example, if we know the rise time, this will be the same fall time or if we know its speed at a point during its ascent, it will be the same when the projectile passes through the same height during its descent. So if a projectile is launched with an initial speed $v_i$, the speed of the projectile when it falls to the same height from where it was launched will be the same, that is, $v_f=v_i$. The above is valid only if the effects of air resistance are negligible.
Therefore from Figure 4.41.
The penguin is about to land higher than the level from which it jumped (the water) with an initial speed $v_i$. If we consider this penguin as a projectile, then its speed $v_f$ just before landing on the ice will be less than the speed with which it jumped out of the water, $v_i>v_f$. In case the ice and the water were at the same height, then $v_i=v_f$.
—
#### Conclusion
The penguin’s speed when it lands on ice is less than its speed when it jumps out of the water.
#### Known
The horizontal movement of a projectile is independent of its vertical movement. While the vertical component of the projectile’s velocity changes with time or height, its horizontal component remains constant.
a) Therefore, if we want the ball to fall into our hands, we must toss it straight upward. So that the horizontal component of the velocity of the ball is the same with which we walk, thus, while the ball goes up and down it will keep moving horizontally with us, since the horizontal component of the speed of the ball will not change.
b) Option C.
—
#### Conclusion
a) We must toss it straight upward.
b) C.
#### Known
The horizontal movement of a projectile is independent of its vertical movement. While the vertical component of the projectile’s velocity changes with time or height, its horizontal component remains constant.
a) Both divers are launched horizontally from the same height, so they will hit the water at the same time. Therefore, since the horizontal distance they travel during the fall depends only on the speed and the time they are in the air:
$$
begin{align*}
d_x=vcdot t
end{align*}
$$
The horizontal distance that diver 2 travels will be twice that of diver 1, since diver 2’s speed, $v_2$, is twice the speed of diver 1, $v_1$, that is, $v_2=2v_1$. This is:
$$
begin{align*}
d_{x,2}=v_2cdot t=2 v_1cdot t=2 d_{x,1}
end{align*}
$$
With:
$$
begin{align*}
d_{x,1}&=v_1cdot thspace{0.5cm}tx{and}hspace{0.5cm} v_2=2 v_1\
&thereforeboxed{d_{x,2}=2 d_{x,1}}
end{align*}
$$
b) Option A.
—
#### Conclusion
a) The horizontal distance that diver 2 travels will be twice that of diver 1.
b) A.
b) A.
#### Known
The magnitude of a vector is its length or size.
#### Calculation
Givens: $l=3.5 tx{cm}$ (side of the chessboard square).
a) From Figure 4.42 we see that displacement 1 consists of two displacements. One up (one box) and one to the left (two boxes). To calculate the magnitude of the displacement 1 (resultant vector) we can use the Pythagorean theorem. While displacement 2 also consists of two displacements. One up (two boxes) and one to the right (one box). The magnitude of displacement 2 is also calculated using Pythagoras. Therefore it is easy to see that the magnitude in both cases is the same.
b) For displacement 1 $vec{D}_1$ we have:
$$
begin{align*}
vec{D}_1=vec{D}_{1U}+vec{D}_{1L}
end{align*}
$$
Where $vec{D}_{1U}$ is the upward displacement, with $D_{1U}=3.5 tx{cm}$ and $vec{D}_{1L}$ is the leftward displacement, with $D_{1L}=7.0 tx{cm}$. The lengths of $vec{D}_{1U}$ and $vec{D}_{1L}$ are measured from the center of each square on the board.
$$
begin{align*}
therefore D_1&=sqrt{D_{1U}^2+D_{1L}^2}=sqrt{(3.5 tx{cm})^2+(7.0 tx{cm})^2}\
&=7.8 tx{cm}
end{align*}
$$
The direction with respect to the upward direction (see Figure 1) is:
$$
begin{align*}
theta&=tx{tan}^{-1}left(frac{D_{1L}}{D_{1U}}right)=tx{tan}^{-1}left(frac{7.0 tx{cm}}{3.5 tx{cm}}right)\
&=63.4^circapprox 63^circ
end{align*}
$$
Therefore, displacement 1 has a direction of $63^circ$ to the left of the upward direction of the board and a magnitude of $7.8 tx{cm}$.
Remember that:
$$
begin{align*}
tx{tan} theta=frac{tx{opposite side}}{tx{adjacent side}}
end{align*}
$$
For displacement 2 $vec{D}_2$ we have:
$$
begin{align*}
vec{D}_2=vec{D}_{2U}+vec{D}_{2R}
end{align*}
$$
Where $vec{D}_{2U}$ is the upward displacement, with $D_{2U}=7.0 tx{cm}$ and $vec{D}_{2R}$ is the rightward displacement, with $D_{2R}=3.5 tx{cm}$.
$$
begin{align*}
therefore D_2&=sqrt{D_{2U}^2+D_{2R}^2}=sqrt{(7.0 tx{cm})^2+(3.5 tx{cm})^2}\
&=7.8 tx{cm}
end{align*}
$$
The direction with respect to the upward direction (see Figure 2) is:
$$
begin{align*}
theta&=tx{tan}^{-1}left(frac{D_{2R}}{D_{2U}}right)=tx{tan}^{-1}left(frac{3.5 tx{cm}}{7.0 tx{cm}}right)\
&=26.6^circapprox 27^circ
end{align*}
$$
Therefore, displacement 2 has a direction of $27^circ$ to the right of the upward direction of the board and a magnitude of $7.8 tx{cm}$.
We can specify the direction of the displacement with respect to another system, for example, a Cartesian x, y system, or a north, south, east and west system, etc.
Graphically:
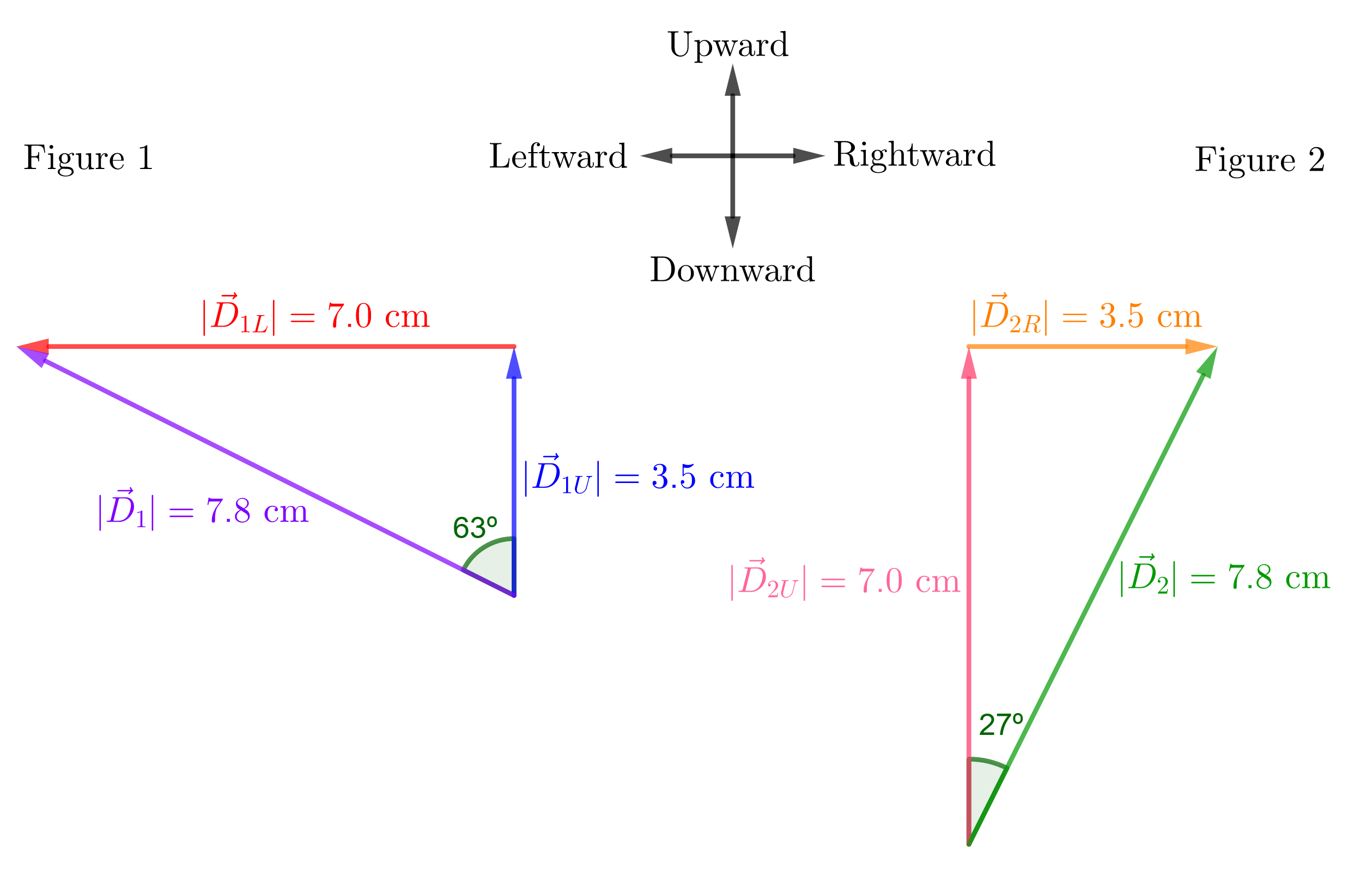
—
#### Conclusion
a) The magnitude of the displacement are equal.
b) $D_1=7.8 tx{cm}$, $theta=63^circ$ to the left of the upward direction.
$D_2=7.8 tx{cm}$, $theta=27^circ$ to the right of the upward direction.
b) $D_1=7.8 text{cm}$, $theta=63^circ$ to the left of the upward direction.
$D_2=7.8 text{cm}$, $theta=27^circ$ to the right of the upward direction.
subsection*{Known}
The horizontal movement of a projectile is independent of its vertical movement. While the vertical component of the projectile’s velocity changes with time or height, its horizontal component remains constant.
subsection*{Calculation}
Givens: a) $v_i=21.5 frac{tx{m}}{tx{s}}$ (for the lob pass). $t_v=3.97 tx{s}$ (flight time). $g=9.81 frac{tx{m}}{tx{s}^2}$. b) $theta=25.0^circ$. From Figure 4.43: $R=35 tx{m}$ (Range).\
a) Flight time is the time it takes for a projectile in the air. This time can be calculated as twice the time the projectile reaches its maximum height, or twice the time it descends from its maximum height to the height from which it was launched (symmetry of the movement of a projectile).\
The time in which a projectile reaches its maximum height can be calculated taking into account that the vertical component of the velocity at this point is zero. Therefore:
begin{align}
v_{y,f}&=v_{y,i}-gcdot t=v_i tx{sin}(theta)-gcdot tnotag\
implies t&=frac{v_i tx{sin}(theta)}{g}, tx{with} v_{y,f}=0 frac{tx{m}}{tx{s}}notag\
therefore t_v&=frac{2v_i tx{sin}(theta)}{g}
end{align}
From (1) we have:
begin{align*}
tx{sin}(theta)=frac{gcdot t_v}{2v_i}implies theta&=tx{sin}^{-1}left(frac{gcdot t_v}{2v_i}right)\
&=tx{sin}^{-1}left[frac{left(9.81 frac{tx{m}}{tx{s}^2}right)(3.97 tx{s})}{2left(21.5 frac{tx{m}}{tx{s}}right)}right]\
&boxed{theta=64.9^circ}
end{align*}
b) The range of a projectile launched at an angle $theta$ and with an initial speed vi is given by:
$$
begin{align*}
R=left(frac{v_i^2}{g}right) tx{sin}(2theta)implies v_i&=sqrt{frac{gcdot R}{tx{sin}(2theta)}}\
&=sqrt{frac{left(9.81 frac{tx{m}}{tx{s}^2}right)(3.5 tx{m})}{tx{sin}(2.25^circ)}}\
&boxed{v_i=21.17 frac{tx{m}}{tx{s}}approx 21.2 frac{tx{m}}{tx{s}}}
end{align*}
$$
c) From the expression (1) we have:
$$
begin{align*}
t_v&=frac{2left(21.17 frac{tx{m}}{tx{s}}right) tx{sin}(25.0^circ)}{9.81 frac{tx{m}}{tx{s}^2}}\
&boxed{t_v=1.82 tx{s}}
end{align*}
$$
We may be tempted to use the equation of range to determine the launch angle in part (a). The problem with using this equation is that we would have two solutions since:
$$
begin{align*}
tx{sin}(theta)=tx{sin}(180^circ-theta)
end{align*}
$$
For example, a projectile launched at a $30^circ$ angle has the same range as when launched at $60^circ$. Therefore to determine at what angle the projectile was launched in part (a) we need some extra information, such as using Figure 4.42 to rule out one of the two angles.
#### Conclusion
a) The launch angle is $64.9^circ$.
b) The initial speed is $21.2 frac{tx{m}}{tx{s}}$.
c) Flight time is $1.82 tx{s}$.
b) The initial speed is $21.2 frac{text{m}}{text{s}}$.
c) Flight time is $1.82 text{s}$.
subsection*{Known}
We can study the vertical motion of a projectile independently of its horizontal motion.\
The range of a projectile is the horizontal distance that the projectile travels during its flight. Therefore, this range will depend on the horizontal speed of the projectile and its time of flight. This is:
begin{align}
R=v_xcdot t_v
end{align}
Where $t_v$ is the flight time and $v_x$ is the horizontal component of the initial velocity.\
The horizontal component of the velocity of a projectile remains constant during its flight and is equal to:
begin{align}
v_x=v_{x,i}=v_i tx{cos}(theta)
end{align}
Where $theta$ is the launch angle.\
While the flight time can vary, depending on whether the projectile falls to the same height from where it was launched or not. For example, if the projectile falls to the same level from where it was launched, we can calculate the flight time as twice the ascent or descent time of the projectile with respect to the point of maximum height (symmetry in the flight of a projectile). This is the point where the vertical component of the velocity becomes zero.\
We have:
begin{align}
v_{y,f}&=v_{y,i}-gcdot t=v_i tx{sin}(theta)-gcdot tnotag\
implies t_{tx{ascent}}&=t=frac{v_i tx{sin}(theta)}{g}
end{align}
With $v_{y,f}=0 frac{tx{m}}{tx{s}}$ at maximum height.
begin{align}
therefore t_v=2t boxed{=frac{2v_i tx{sin}(theta)}{g}}
end{align}
From (1), (2) and (4) we have:
$$
begin{align*}
R&=(v_i tx{cos}(theta))left(frac{2v_i tx{sin}(theta)}{g}right)\
&=frac{(v_i^2)(2 tx{sin}(theta) tx{cos}(theta))}{g}=left(frac{v_i^2}{g}right) tx{sin}(2theta)
end{align*}
$$
With:
$$
begin{align*}
tx{sin}(2theta)=2 tx{sin}(theta) tx{cos}(theta)
end{align*}
$$
Therefore, the maximum range $R_{tx{max}}$ of the projectile when it falls to the same height from where it was launched, will occur when the launch angle is $45^circ$.
$$
begin{align*}
boxed{R_{tx{max}}=frac{v_i^2}{g}}
end{align*}
$$
The two cases discussed below are with this $45^circ$ angle. We will first have the case when the projectile lands at a higher height or level with respect to the height from where it was launched. The key here is to analyze the projectile’s time of flight, since the horizontal component of the velocity is constant.
As we already know, the flight time is the time in which the projectile rises to its maximum height and lands at a height or level with respect to which it was launched. Therefore, this flight time can be calculated as the sum of the ascent time and the descent time. The ascent time is already calculated in (3), while the descent time will depend on the height where the projectile lands. Therefore we will have:
$$
begin{align*}
t_v=t_{tx{ascent}}+t_{tx{descent}}
end{align*}
$$
The projectile descent time is the time in which it goes from its maximum height to the landing height. Therefore we have:
$$
begin{align*}
&y_f=y_i-v_{y,i}cdot t-frac{gcdot t^2}{2}=y_i-frac{gcdot t^2}{2}\
&implies t=sqrt{frac{2(y_f-y_i)}{-g}}
end{align*}
$$
Where we are now analyzing the movement of the projectile from its maximum height to the landing point. This implies that the projectile begins to fall with the vertical component of the initial velocity $v_{y,i}=0 frac{tx{m}}{tx{s}}$ (the negative sign is because this component is in the negative direction equal to the acceleration of gravity). The vertical position $y_i$ is the position of the maximum height and the position $y_f$ is the landing position of the projectile.
Therefore, using the previous result, we have that the descent time is:
$$
begin{align*}
t_{tx{descent}}=sqrt{frac{2(y_f-y_i)}{-g}}=sqrt{frac{2(y-h_{tx{max}})}{-g}}
end{align*}
$$
Where we have changed the notation so as not to cause confusion with what we will do next. Finally:
$$
begin{align*}
boxed{t_{tx{descent}}=sqrt{frac{2(y-h_{tx{max}})}{-g}}}
end{align*}
$$
With $y$, the position of the projectile where we want to calculate the time of fall and $h_{tx{max}}$, the maximum height of the projectile. We can see this time is always positive since:
$$
begin{align*}
&y-h_{tx{max}}0
end{align*}
$$
Where we place the origin of coordinates at the projectile launch point, so $y$ is positive above this point and negative below.
We can calculate the point of maximum height $h_{tx{max}}$, in terms of the initial launch velocity and the launch angle, taking into account that this point is the final position $y_f$ of the projectile when it ascends.
Therefore, during the ascent stage we have:
$$
begin{align*}
v_{y,f}^2&=v_{y,i}^2-2g(y_f-y_i)\
&=(v_i tx{sin}(theta))^2-2g(y_f-y_i)\
implies &boxed{y_f=frac{(v_i tx{sin}(theta))^2}{2g}=h_{tx{max}}}
end{align*}
$$
With $y_i=0 tx{m}$ and $v_{y,f}=0 frac{tx{m}}{tx{s}}$.
Substituting this expression in the descent time $t_{tx{descent}}$ we have:
$$
begin{align*}
t_{tx{descent}}&=sqrt{frac{2left[y-frac{(v_i tx{sin}(theta))^2}{2g}right]}{-g}}\
&=sqrt{frac{2gcdot y-(v_i tx{sin}(theta))^2}{-g^2}}\
&boxed{therefore t_{tx{descent}}=frac{1}{g}sqrt{(v_i tx{sin}(theta))^2-2gcdot y}}
end{align*}
$$
Finally we have an expression for the flight time of a projectile that falls in the vertical position $y$ (height), with respect to the initial position $y_i=0 tx{m}$ (zero height).
$$
begin{align*}
&t_v=t_{tx{ascent}}+t_{tx{descent}}\
implies &boxed{t_v=frac{v_i tx{sin}(theta)}{g}+frac{1}{g}sqrt{(v_i tx{sin}(theta))^2-2gcdot y}}
end{align*}
$$
From the previous expression we can see that if the projectile falls to the same level from which it started, then the expression reduces to what we already know and saw in (3), that is:
For $y=y_i=0 tx{m}$.
$$
begin{align*}
t_v&=frac{v_i tx{sin}(theta)}{g}+frac{1}{g}sqrt{(v_i tx{sin}(theta))^2-2g(0 tx{m})}\
t_v&=frac{v_i tx{sin}(theta)}{g}+frac{v_i tx{sin}(theta)}{g}=frac{2v_i tx{sin}(theta)}{g}
end{align*}
$$
Therefore, from (1), we see that the range of a projectile launched with an initial velocity $v_i$ and with an angle $theta$, which falls at a height $y$ with respect to the height where it began its flight is:
$$
begin{align*}
R&=v_xcdot t_v\
&=(v_i tx{cos}(theta))left[frac{v_i tx{sin}(theta)}{g}+frac{1}{g}sqrt{(v_i tx{sin}(theta))^2-2gcdot y}right]\
&boxed{therefore R=frac{v_i tx{cos}(theta)}{g}left[v_i tx{sin}(theta)+sqrt{(v_i tx{sin}(theta))^2-2gcdot y}right]}
end{align*}
$$
Using the maximum range angle $theta=45^circ$, we have:
$$
begin{align*}
&R_{tx{max}}=frac{v_i}{g}left(frac{sqrt{2}}{2}right)left[v_ileft(frac{sqrt{2}}{2}right)+sqrt{frac{v_i^2}{2}-2gcdot y}right]\
&boxed{therefore R_{tx{max}}=frac{v_i^2}{2g}+frac{sqrt{2}v_i}{2g}sqrt{frac{v_i^2}{2}-2gcdot y}}
end{align*}
$$
That at $y=0 tx{m}$ reduces to:
$$
begin{align*}
boxed{R_{tx{max}}=frac{v_i^2}{g}}
end{align*}
$$
All of the above is valid also in the case where the projectile falls at a lower level or height with respect to where it was launched. Taking into account that we take the launch height level at $y_i=0 tx{m}$, the landing position will now have negative values $y<0$. Therefore for positions $y$ below the launch level, we have:
$$
begin{align*}
R=frac{v_i tx{cos}(theta)}{g}left[v_i tx{sin}(theta)+sqrt{(v_i tx{sin}(theta))^2+2g|y|}right]\
implies R_{tx{max}}=frac{v_i^2}{2g}+frac{sqrt{2}v_i}{2g}sqrt{frac{v_i^2}{2}+2g|y|}
end{align*}
$$
For $y<0$, or we can simply work with the positions below the launch level with the negative sign and leave the negative in the equation of the range.
In the case of considering the air resistance in the range of the projectile, the analysis becomes more complicated. Especially when we want to obtain analytical expressions like the ones we obtained previously, since we have to introduce the friction force of the air in the projectile’s equations of motion.
Therefore we will only say that when the effects of air resistance are taken into account, both the range of the projectile and its maximum height are reduced. Another important consequence of the effects of the air is that the symmetry in the flight of the projectile is broken, that is, for a projectile that lands at the same level from which it was launched, the rise time is different from the descent time, also the landing speed is also different from how fast it was launched. Furthermore, the trajectory is more complicated, since it is no longer an “ideal” parabola. Finally, we will say that the maximum range does not necessarily occur for $theta=45^circ$.
—
#### Conclusion
The maximum range of a projectile without air resistance, depending on the level where $y$ lands with respect to the launch level $y_i$, is given by:
$$
begin{align*}
boxed{R_{tx{max}}=frac{v_i^2}{2g}+frac{sqrt{2}v_i}{2g}sqrt{frac{v_i^2}{2}-2gcdot y}}
end{align*}
$$
Therefore the maximum range will be greater when the projectile lands at a height level below the level from which it was launched. The range will be less when it lands higher from where it was launched. The two previous cases compared to the case when the projectile lands at the same level where it was launched.
When air resistance is considered, both the maximum height of the projectile and its maximum range are reduced.
Figures 1, 2, 3 show the three cases studied. Figure 1, when the projectile lands at a height greater than $y_i$. Figure 2, when the projectile lands at a height equal to $y_i$. Figure 3 when the projectile lands at a height less than $y_i$. The projectile is launched at an angle of $45^circ$ and with an initial speed of $40 frac{tx{m}}{tx{s}}$, with $g=10 frac{tx{m}}{tx{s}^2}$ and without the friction of the air.
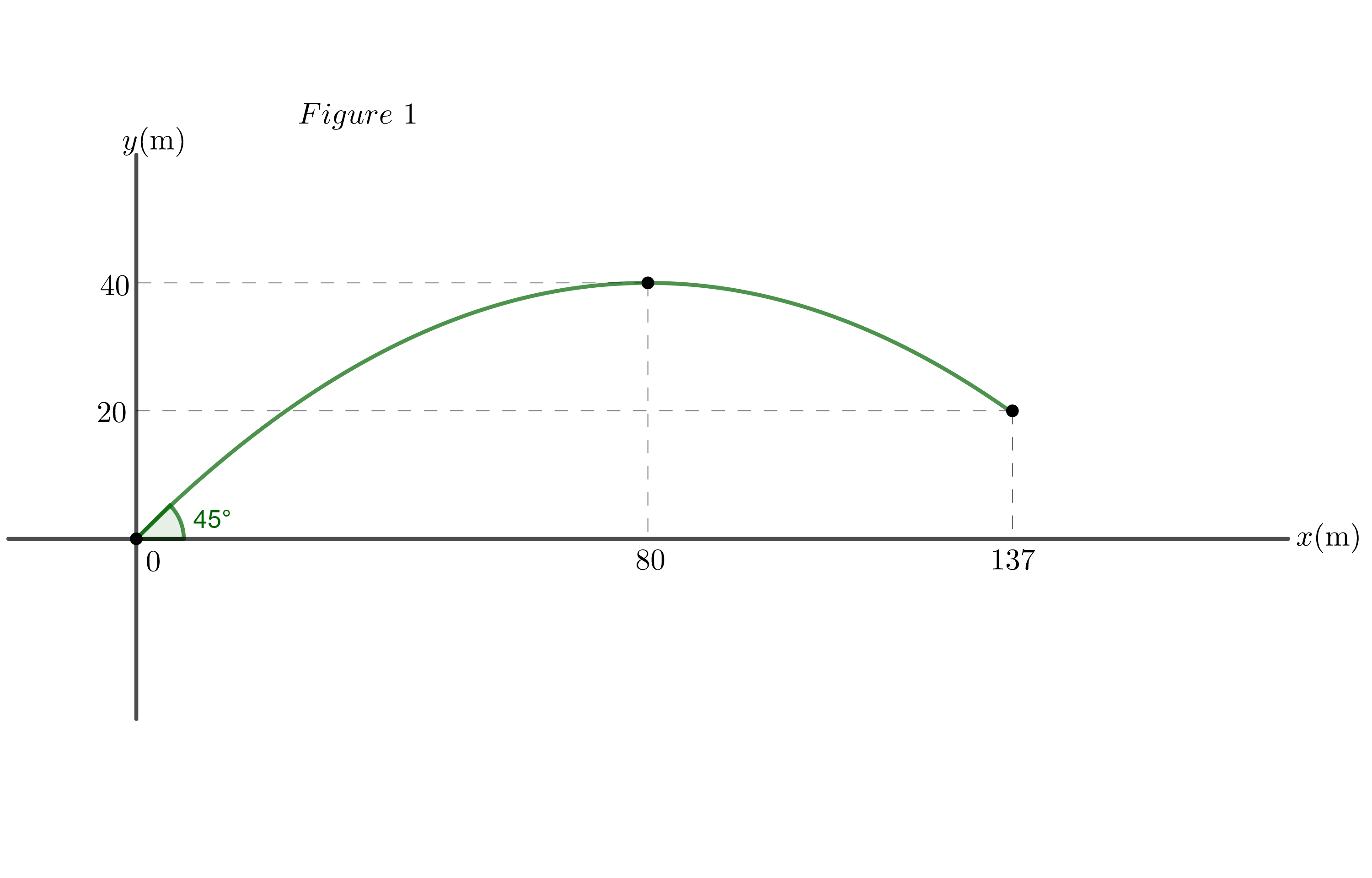
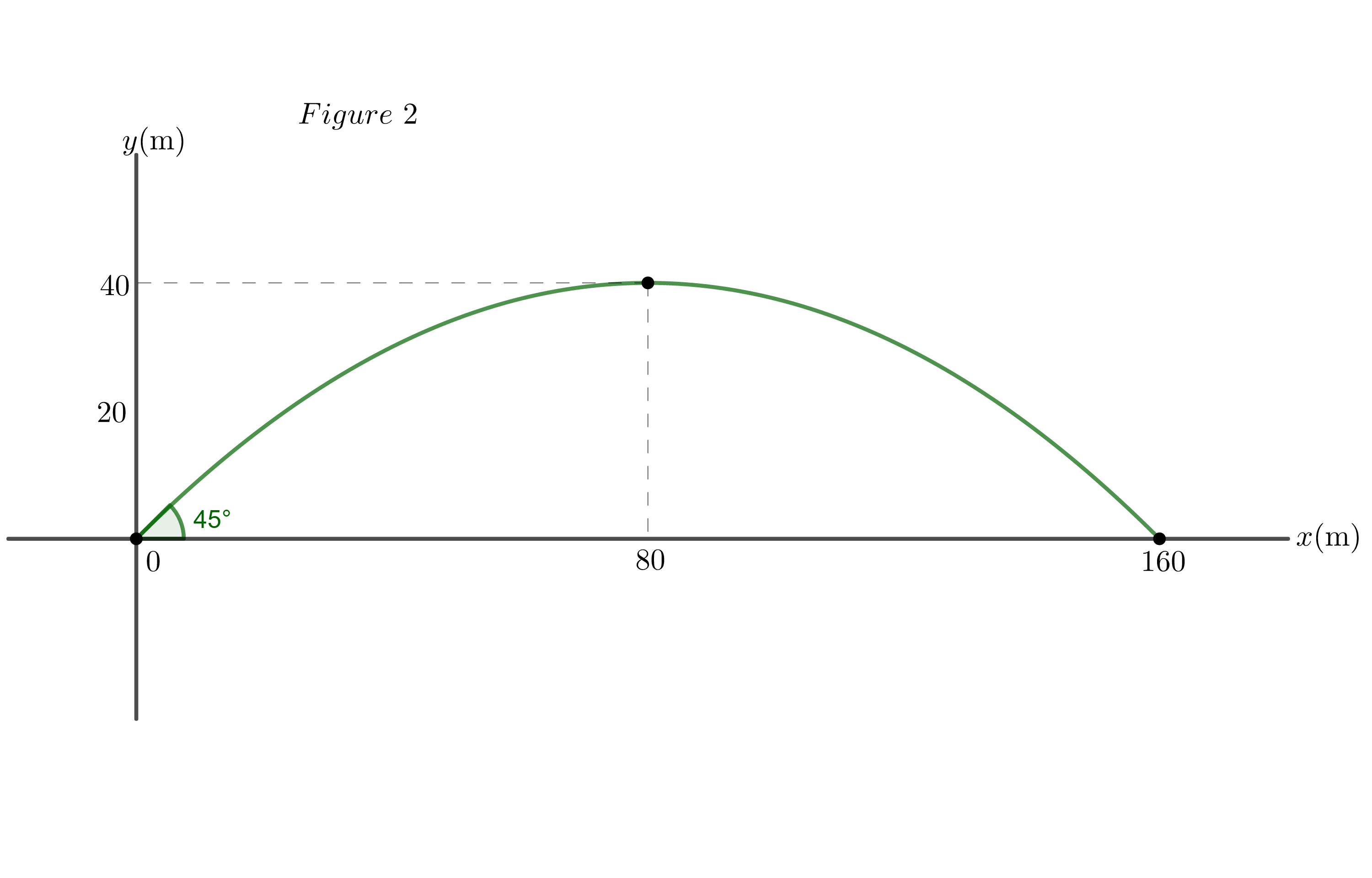

When air resistance is considered, both the maximum height of the projectile and its maximum range are reduced.
#### Known
Neglecting air resistance, a projectile will move is such a way that its horizontal and vertical motions are independent. Therefore while the vertical component of velocity changes with time or height, the horizontal component remains constant.
The acceleration of gravity can be considered constant at all points near the surface of the earth and in a downward direction (radial direction towards the center of the earth). This implies that the acceleration of a projectile is equal to the acceleration of gravity at all times in its trajectory.
From the above we can see that:
The horizontal component of the velocity of the keys when they fall is the same as the constant velocity of us while walking. Therefore, we will observe how the keys fall next to us until they reach the ground. This is because for us the set of keys does not have a horizontal component of velocity, so they will fall vertically right at our feet.
The falling time of the set of keys does not depend on our forward motion, be it faster or slower, since as we mentioned, the motion in the horizontal axis is independent of the motion in the vertical axis.
The acceleration of the set of keys will not be affected by our forward movement or our movement in any other direction, as long as it is with constant speed. If we start to accelerate our pace, the keys will fall with an acceleration other than $g$ (gravity).
—
#### Conclusion
The set of keys will fall right at our feet.
The drop time of the set of keys does not depend on our forward movement.
The acceleration of the set of keys is the acceleration of gravity regardless of our forward motion.
The drop time of the set of keys does not depend on our forward movement.
The acceleration of the set of keys is the acceleration of gravity regardless of our forward motion.
subsection*{Known}
Flight time is the time it takes for a projectile in the air. This time can be calculated as twice the time in which the projectile reaches its maximum height or twice the time in which it descends from its maximum height to the height from where it was firing (symmetry of the movement of a projectile).\
The time in which a projectile reaches its maximum height can be calculated taking into account that the vertical component of the velocity at this point is zero. Therefore:
begin{align}
v_{y,f}&=v_{y,i}-gcdot t=v_i tx{sin}(theta)-gcdot tnotag\
implies t&=frac{v_i tx{sin}(theta)}{g}, tx{with} v_{y,f}=0 frac{tx{m}}{tx{s}}notag\
therefore t_v&=frac{2v_i tx{sin}(theta)}{g}
end{align}
Where $g=9.81 frac{tx{m}}{tx{s}^2}$ is the acceleration of gravity on Earth, we would have another value elsewhere.
subsection*{Calculation}
Givens: $v_i=9.92 frac{tx{m}}{tx{s}}$. $theta=75.0^circ$. $g=3.72 frac{tx{m}}{tx{s}^2}$ (Mars gravity).\
From Figure 4.44 we see that the time elapsed between the first and second bounce is the flight time. From (1) we have:
begin{align*}
t_v&=frac{2left(9.92 frac{tx{m}}{tx{s}}right) tx{sin}(75.0^circ)}{3.72 frac{tx{m}}{tx{s}^2}}\
&=5.15 tx{s}
end{align*}
vspace{2pt}
hrule
vspace{1pt}
subsection*{Conclusion}
Option C.\
On Earth this time would be less.
#### Known
The range of a projectile is determined by:
$$
begin{align}
R=left(frac{v_i^2}{g}right) tx{sin}(2theta)
end{align}
$$
Where $g=9.81 frac{tx{m}}{tx{s}^2}$ is the acceleration of gravity on Earth, we would have another value elsewhere.
#### Calculation
Givens: $v_i=9.92 frac{tx{m}}{tx{s}}$. $theta=75.0^circ$. $g=3.72 frac{tx{m}}{tx{s}^2}$ (Mars gravity).
From (1) we have:
$$
begin{align*}
R&=left[frac{left(9.92 frac{tx{m}}{tx{s}}right)^2}{3.72 frac{tx{m}}{tx{s}^2}}right] tx{sin}(2cdot 75.0^circ)\
&=13.2 tx{m}
end{align*}
$$
—
#### Conclusion
Option A.
On Earth, the rover would have traveled a shorter distance.
subsection*{Known}
The maximum height that a projectile reaches can be determined taking into account that at this point, the vertical component of the projectile’s velocity is zero.
begin{align}
&v_{y,f}^2=v_{y,i}^2-2g(y_f-y_i)notag\
&implies y_f-y_i=frac{v_{y,f}^2-v_{y,i}^2}{-2g}, tx{with} v_{y,i}=v_i tx{sin}(theta)
end{align}
Where $g=9.81 frac{tx{m}}{tx{s}^2}$ is the acceleration of gravity on Earth, we would have another value elsewhere.
subsection*{Calculation}
Givens: $v_i=9.92 frac{tx{m}}{tx{s}}$. $theta=75.0^circ$. $g=3.72 frac{tx{m}}{tx{s}^2}$ (Mars gravity). $y_i=0 tx{m}$. $v_{y,f}=0 frac{tx{m}}{tx{s}}$\
From (1) we have:
begin{align*}
y_f-0 tx{m}&=frac{0 frac{tx{m}}{tx{s}}-left[left(9.92 frac{tx{m}}{tx{s}}right)tx{sin}(75^circ)right]^2}{-2left(3.72 frac{tx{m}}{tx{s}^2}right)}\
&boxed{y_f=12.3 tx{m}}
end{align*}
vspace{2pt}
hrule
vspace{1pt}
subsection*{Conclusion}
Option C.\
The maximum height on Earth would be less.

