
All Solutions
Page 590: Assessment
the incident and reflected beam is $2theta_{i}$. So here we have
$$
begin{align*}
& 2theta_{i}=28text{textdegree}\
Rightarrow & theta_{i}=frac{28text{textdegree}}{2}=14text{textdegree}
end{align*}
$$
So the angle of incidence is $14text{textdegree}$
tt{The law of reflection states that $theta_i=theta_r$ both angles are calculated to the normal therefore the total angle that they form is $theta_i+theta_r=2theta_i=2*23=boxed{46^o}$ }
$$
46^o
$$
tt{the angle of reflection $theta_r$ is calculated to the normal of the mirror plane, therefore the angle between the ray and the mirror plane is $90-theta_r=90-37=53^o$}
$$
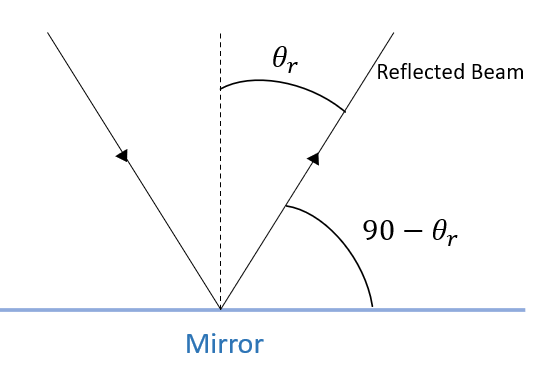
53^o
$$
tt{We have: $tan15^o=frac{x}{68}$}
$$
$$
Rightarrow x=68tan15^o=18.22cm
$$
$x$ Defines the horizontal component of the distance travelled by the light before changing it’s direction upon meeting any of the mirrors. We will calculate how many times $N$ the light beam changes its direction:
$$
N= frac{168}{x}=frac{168}{18.22}=9.22
$$
Based on the figure, the light beam reflects 5 times from the top mirror and 4 times from the button mirror.
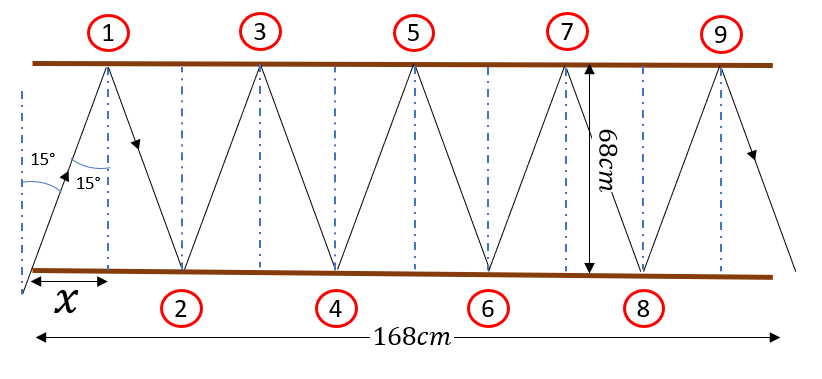
tt{(a)5,(b)4}
$$

$$
tantheta=frac{text{opposite side}}{text{adjacent side}}
$$
$$
tt{Looking into the figure below we can than write:
$$tan32^o=frac{h}{2}$$}
$$
$$
Rightarrow h=2tan32^o
$$
when the mirror is tilted by $5^o$ we have:
$$
tan^o37=frac{h+Delta_y}{2}
$$
$$
h+Delta_y=2tan37^o
$$
$$
Rightarrow Delta_y=2(tan37^o-tan32^o)=boxed{0.26m}
$$
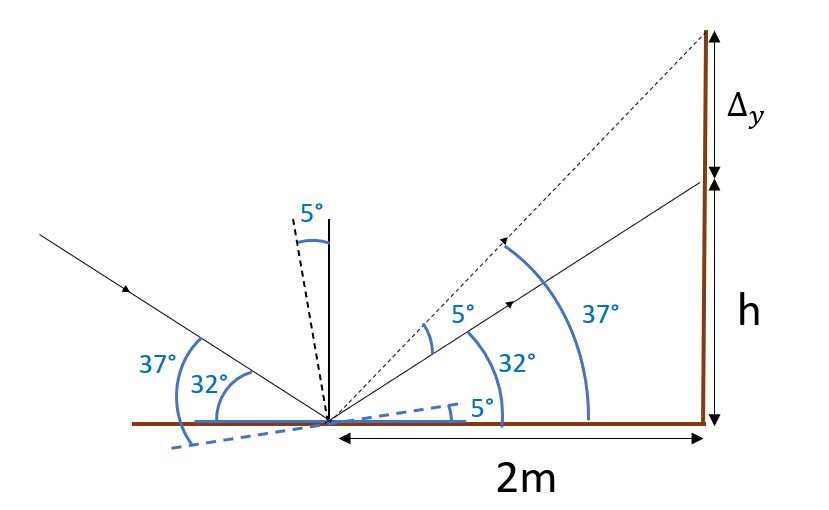
Delta_y=0.26m
$$
Hence the image distance will also be 1 m, $textit{i.e. }$the image will
be formed 1 m behind the mirror. Hence the distance between me and
my image is
$$
d=(1 {rm m})+(1 {rm m})=2 {rm m}
$$
tt{when we move at a speed of $2.6frac{m}{s}$ towards the mirror, the reflection moves toward the mirror in the other direction with a speed of $2.6frac{m}{s}$, since speed is always positive we can say that the person and the reflection are approaching each other at a total speed of $$2.6+2.6=5.2frac{m}{s}$$ }
$$
5.2frac{m}{s}
$$
tt{In order to have a clear a picture of the sister’s Reflection, Your Camera should be focused on the sister’s Reflection plane, consequentially we have to calculate the distance between you and your sister’s Reflection:
$$2+1.5+1.5=boxed{5m}$$ }
$$
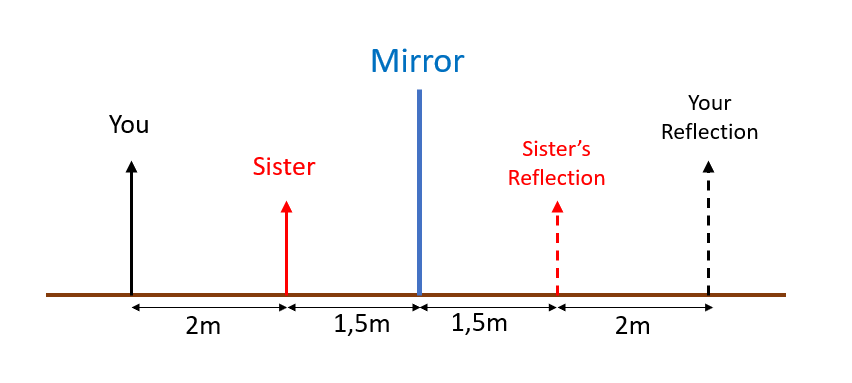
tt{5m}
$$
$$
begin{align*}
theta_{text{r}} = theta_{text{i}}
end{align*}
$$
$$
begin{align*}
tan theta_{text{i}} = frac{w_{text{mirror}}}{d_{text{eye}}}
end{align*}
$$
where $w_{text{mirror}}$ is the width of the mirror and $d_{text{eye}}$ is the distance of the driver’s eye from the mirror.
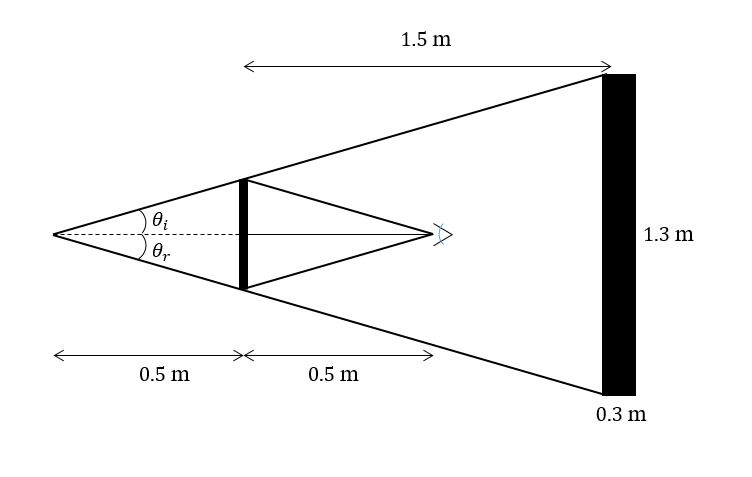
$$
begin{align*}
tan theta_{text{r}} = frac{w_{text{window}}}{d_{text{eye}}+d_{text{window}}}
end{align*}
$$
where $w_{text{window}}$ is the width of the window and $d_{text{window}}$ is the distance between the rear window and the mirror.
$$
begin{align*}
tan theta_{text{i}} &= tan theta_{text{r}} \ frac{w_{text{mirror}}}{d_{text{eye}}} &= frac{w_{text{window}}}{d_{text{eye}}+d_{text{window}}}
end{align*}
$$
$$
begin{align*}
w_{text{mirror}} &= frac{w_{text{window}}d_{text{eye}}}{d_{text{eye}}+d_{text{window}}} \ &= frac{(1.3;text{m})(0.50;text{m})}{0.50;text{m}+1.50;text{m}} \ &= boxed{0.33;text{m};text{or } 33;text{cm}}
end{align*}
$$
$$
begin{align*}
tan theta_{text{i}} = frac{h_{text{mirror}}}{d_{text{eye}}}
end{align*}
$$
where $h_{text{mirror}}$ is the height of the mirror.
$$
begin{align*}
tan theta_{text{r}} = frac{h_{text{window}}}{d_{text{eye}}+d_{text{window}}}
end{align*}
$$
where $h_{text{window}}$ is the height of the rear window.
$$
begin{align*}
tan theta_{text{i}} &= tan theta_{text{r}} \ frac{h_{text{mirror}}}{d_{text{eye}}} &= frac{h_{text{window}}}{d_{text{eye}}+d_{text{window}}}
end{align*}
$$
$$
begin{align*}
h_{text{mirror}} &= frac{h_{text{window}}d_{text{eye}}}{d_{text{eye}}+d_{text{window}}} \ &= frac{(0.3;text{m})(0.50;text{m})}{0.50;text{m}+1.50;text{m}} \ &= boxed{0.075;text{m};text{or } 7.5;text{cm}}
end{align*}
$$
$$
theta_i=theta_rRightarrow tan{theta_i}=tan{theta_r}Rightarrow frac{frac{0.32}{2}}{0.5}=frac{frac{H}{2}}{95}Rightarrow H=60.8m
$$
H=60.8m
$$
$$
begin{align*}
tan frac{theta}{2} = frac{y}{d}
end{align*}
$$
$$
begin{align*}
d = frac{y}{tan frac{theta}{2}} = frac{5.5;text{cm}}{tan 13.5text{textdegree}} = boxed{23;text{cm}}
end{align*}
$$
tt{if the distance of the image to the mirror is positive $d_i>0$ then the image is real and is situated in front of the mirror \ if the distance of the image to the mirror is negative $d_i<0$ then the image is virtual and situated behind the mirror. }
$$
tt{the sign determines the type of the image (real-virtual) and if the image is in front/behind the mirror.}
$$
$m0$ then the image is upright (because $h_i$ and $h_o$ have same signs).
tt{the sign of the magnification determines whether the image is inverted or upright}
$$
We know that $d_o$ is always positive, therefore the value of $f$ will determine if the image will be real or virtual.
In a convex mirror $f<0 Rightarrow d_i=frac{fd_o}{f-d_o}0$ therefore the sign of $d_i$ is determined by the term $f-d_o$:
if $f>d_oRightarrow d_i>0$ The image is real.
if $f<d_oRightarrow d_i<0$ The image is virtual.
tt{A concave mirror can produce a real image if the object mirrored is placed farther than its focal point}
$$
tt{Referring to {color{#4257b2}{Figure16.20}} We can see that all incident rays coming from a distant object (like the sun in our example) are reflected and intersect at the focal point $F$ specific to the concave mirror used. \When an object absorbs visible light it converts its short-wavelength into a long heat wavelength, Therefore having more beams focused at the same place causes more heat generation at the aforementioned place and increases the chances to ignite a fire .}
$$
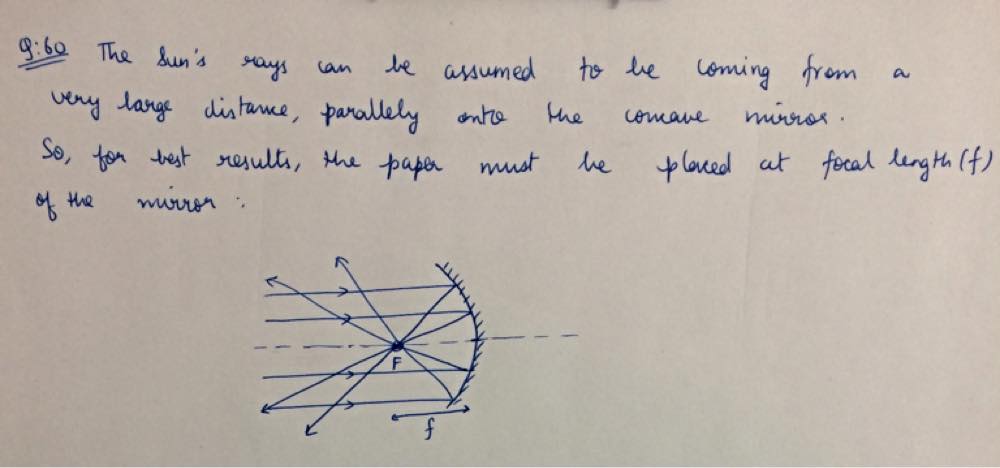
tt{Rays coming from very distant objects can be treated as parallel rays when they encounter the mirror surface. As show in {color{#4257b2}{Figure 16.21}} the convex mirror is not good for collecting light because the reflected rays are scattered, on the other hand in {color{#4257b2}{Figure 16.20}} the concave mirror will reflect all incident light to its focal point making it a good choice for collecting light. }
$$
tt{concave mirror}
$$
(a) inverted
(b) reduced
(c) real.
tt{the image is (a) inverted (b) reduced, (c) real.}
$$
Given that the mirror is convex we can also state that: $f=-frac{1}{2}R$
the equation becomes :$d_i=frac{-R}{2}frac{d_o}{d_0-frac{R}{2}}$
since the object will be far from the mirror we can say that $d_0>>R Rightarrow frac{d_o}{d_0-frac{R}{2}} approx frac{d_o}{d_0}=1$
$$
d_i=boxed{-frac{R}{2}}
$$
d_i=-frac{R}{2}
$$
Per definition $d_i$ is the distance between the mirror and the image, moreover, since the mirror is convex then $d_i<0$ so if $d_idownarrow$ the image gets farther from the mirror and moves to the right
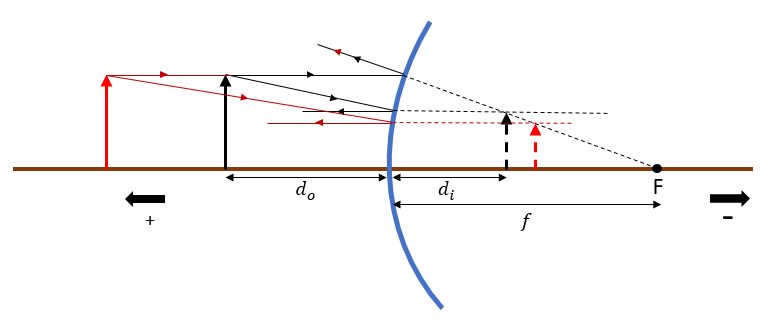
tt{the image moves to the right }
$$
(a) in a concave mirror we have $f=frac{1}{2}R$, point 2 sits in the middle between the mirror and point 1 therefore it can be the focal point (point 3 does not suffice the condition)
(b) We deduce that point 1 is C.
tt{(a) 2, (b) 1 }
$$
tt{To determine which of the candidates (Green Arrows) represent the real image of the object (Red Arrow), we proceed by Drawing the Principal Rays. \
textit{Parallel ray:}the incident light is parallel to the mirror’s principal axis, it is reflected by the mirror such as its extension passes by the mirror’s focal point.\
textit{Focal point ray:}the incident line passes through the focal point (in this case the line’s extension) the reflected ray is parallel to the mirror’s principal axis \
$Rightarrow$ The intersection of both rays determines the object’s reflection.
}
$$
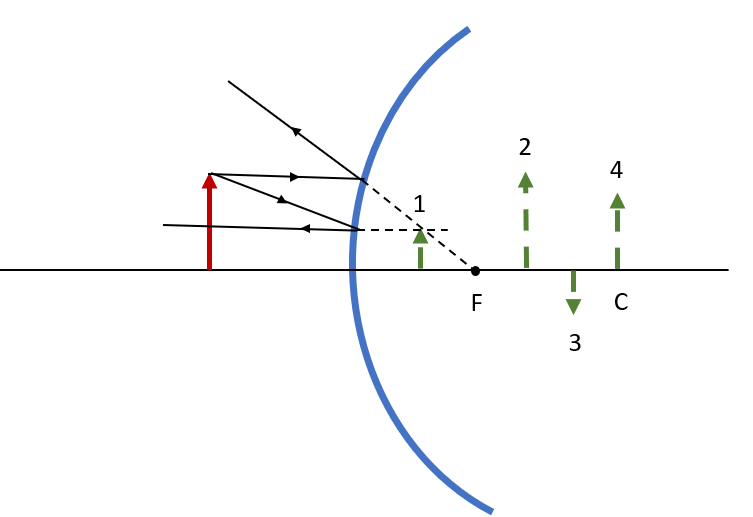
tt{Image 1}
$$
tt{The center of curvature of the reflecting globe is inside the globe itself, we can say then that at every section of the globe that the center of curvature is behind the reflecting surface, consequentially we can consider the globe a convex mirror at any section. For a convex mirror $f=-frac{R}{2}=-frac{D}{4}=boxed{-7.88 cm}$}
$$
f=-7.88cm
$$
tt{ From {color{#4257b2}{Figure 16.20}} we can see that the focal point, F, is halfway between
the center of curvature, C, and mirror surface.\
The center of curvature is simply the center of the theoretical sphere that the mirror was cut from
\ According to the Focal Length for a Concave Mirror of Radius R we have : $$f=frac{R}{2}Rightarrow R=2f=2*12=boxed{24cm}$$}
$$
R=24cm
$$
the center of curvature, C, and mirror surface.
The center of curvature is simply the center of the theoretical sphere that the mirror was cut from
Applying the formula for Focal Length for a Convex Mirror of Radius R we have :
$$
f=-frac{R}{2}=-frac{28}{2}=boxed{-14cm}
$$
f=-14cm
$$
The magnifying equation states $$m=frac{h_i}{h_o}=-frac{d_i}{d_o}$$ }$
The object is placed infront of the mirror $d_o=33cm$ and the image apprears behind the mirror therefore it is Virtual $d_i0Rightarrow$ The image is upright.
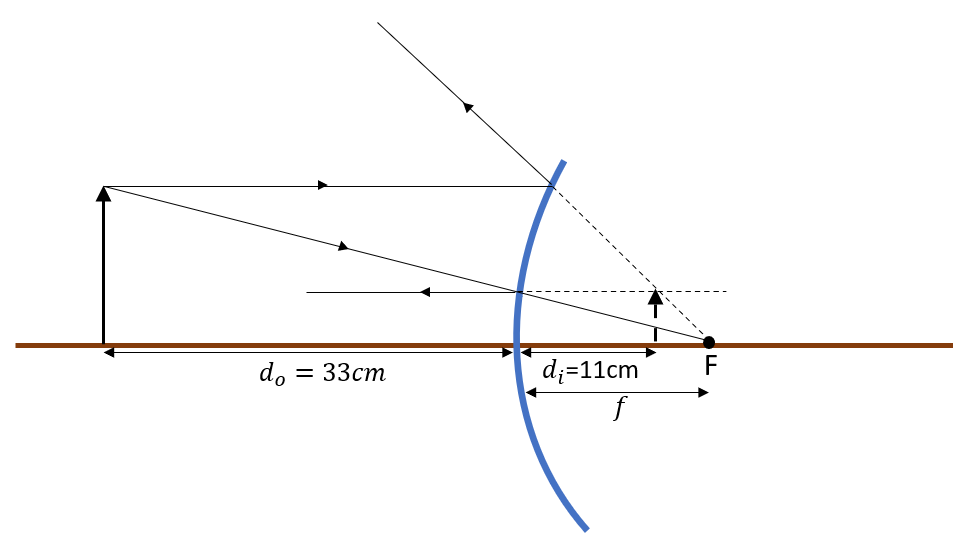
tt{The image is upright}
$$
The magnifying equation states: $$m=frac{h_i}{h_o}=-frac{d_i}{d_o}$$ .}$
it is mentioned that the image is real therefore:
$$
d_i>0Rightarrow m=-frac{12}{24}=-frac{1}{2}
$$
$m<0Rightarrow$The image is inverted.
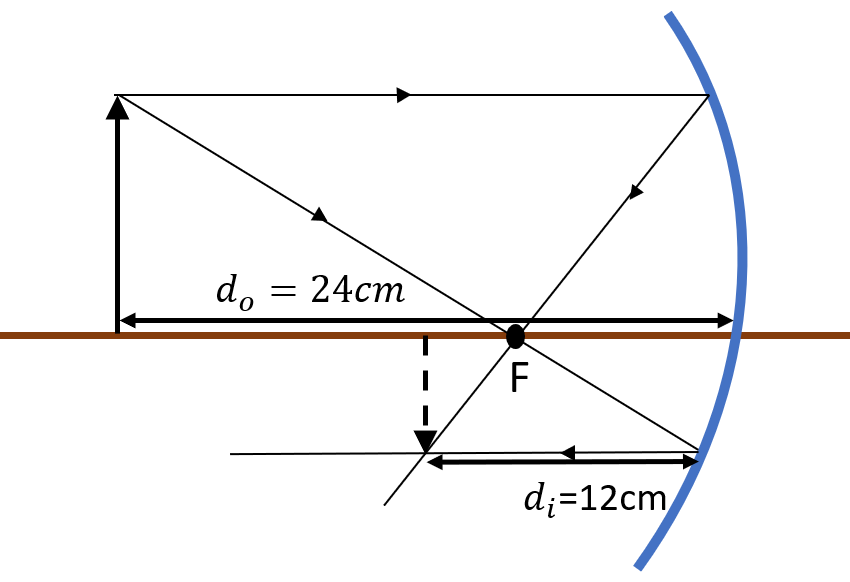
tt{The image is inverted}
$$
tt{We first determine the focal length of the concave mirror:}
$$
$$
f=frac{R}{2}=frac{40}{2}=20cm
$$
Using the mirror equation we can determine the postion of the image:
$$
frac{1}{f}=frac{1}{d_i}+frac{1}{d_o}
$$
$$
Rightarrow frac{1}{d_i}=frac{1}{f}-frac{1}{d_o}=frac{d_o-f}{d_of} Rightarrow d_i=frac{d_of}{d_o-f}
$$
$$
Rightarrow d_i=frac{30*20}{30-20}=60cm
$$
$Rightarrow d_i>0$, The image is located 60cm in front of the mirror.
$text{color{#4257b2}{Parallel Ray}}$: The parallel ray is reflected along a line that extends to the focal point behind the mirror.
$text{color{#4257b2}{Focal-point Ray}}$: We will have to extend the focal point ray through the convex mirror since the real ray is reflected parallel to the mirror axis and does not reach in reality the focal point.
$text{color{#4257b2}{Center of curvature Ray}}$: The same thing for this ray, the direction of the ray passes through the center of curvature by extension only.
$Rightarrow$ the intersection point of these rays determines the position and size of the image.
Data for the Diagram:
convex mirror:$f=-0.5text{ m}$.
Object distance: $d_o=2text{ m}$.
Object height; $h_o=42text{ cm}.$
Diagram Scale
Horizontally: $1text{ m}longrightarrow 2text{ cm}$.
Vertically: $10text{ cm}longrightarrow 0.1text{ cm}$.
(a)Results:
Object location:40 cm.
Object height: 10 cm.
(b) Image is upright.
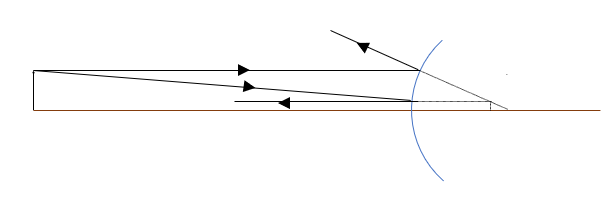
tt{The mirror equation state:}
$$
$$
frac{1}{f}=frac{1}{d_o}+frac{1}{d_i}
$$
We know that the mirror is convex $Rightarrow f<0$
We will solve the mirror equation for the position of the image $d_i$:
$$
frac{1}{d_i}=frac{1}{f}-frac{1}{d_o}=frac{d_o-f}{fd_o}Rightarrow d_i=frac{fd_o}{d_o-f}
$$
$$
Rightarrow d_i=frac{(-0.5)2}{2+0.5}=boxed{-0.4m}
$$
The magnification equation state:
$$
m=frac{h_i}{h_o}=-frac{d_i}{d_o}
$$
We will solve the magnification equation for the height of the image $h_i$:
$$
Rightarrow h_i=-frac{h_od_i}{d_o}=frac{0.42*(-0.4)}{2}=0.084m=boxed{8.4cm}.
$$
d_i=-0.4m,h_i=8.4cm
$$
The sun is very distant from the earth and we can safely assume that the rays are coming from infinity and are parallel to each other.
$text{color{#4257b2}{Figure 16.21}}$ illustrates the situation in hand and therefore we can say that all incoming rays from the sun have to converge at the focal point of the helmet, where the image of the sun is formed.
$$
f=-4.8cm
$$
Using the relation between the focal length $f$ and $R$ the radius of curvature we deduce that:
$$
f=-frac{R}{2}Rightarrow R=-2f=boxed{9.6cm}
$$
R=9.6cm
$$
$text{color{#4257b2}{Plane mirror:}}$ for this type of mirror we know that $d_i=-d_o$ for all values of $d_o$ ,plotting this equation yield a decreasing linear function, this result does not conform with function plotted in the exercise
$text{color{#4257b2}{Convex mirror:}}$ for this type of mirror we know that $d_i<0$ for all values of $d_o$, contrary to the function plotted in the exercise that has positive values of $d_i$
$Rightarrow$ The function is of a $text{color{#4257b2}{Concave mirror}}$
(b) Using the mirror equation we want to define $d_i$ as a function of $d_o$:
$$
frac{1}{f}=frac{1}{d_o}+frac{1}{d_i}Rightarrow frac{1}{d_i}=frac{d_o-f}{fd_o}Rightarrow d_i=frac{fd_o}{d_o-f}
$$
According to $text{color{#4257b2}{Table 16.1}}$ If the object is to be placed around the focal point then the object image is projected to infinity, in other words:
$$
begin{equation*}
lim_{d_orightarrow f}{frac{fd_o}{d_0-f}=infty}
end{equation*}
$$
$$
begin{equation*}
lim_{d_orightarrow f}{d_i=infty}
end{equation*}
$$
We can therefore determine $f$ from the figure to be approximately $boxed{0.3cm}$
f=0.3cm
$$

We will use the magnifying equation to determine the image position from the mirror $d_i$:
$$
m=-frac{d_i}{d_o}Rightarrow d_i=-md_o=-0.25*32=-8cm
$$
We use now the mirror equation to determine the focal length:
$$
frac{1}{f}=frac{1}{d_o}+frac{1}{d_i}=frac{d_i+d_o}{d_id_o}
$$
$$
Rightarrow f=frac{d_id_o}{d_i+d_o}=frac{(-8)*32}{-8+32}=-11cm
$$
Finally we use the relation between the focal length and the radius of curvature for a convex mirror:
$$
f=-frac{R}{2}Rightarrow R=-2f=boxed{22cm}
$$
R=22cm
$$
{color{#4257b2}{Table 16.1}} sums up the characteristics of both concave and convex mirrors and we can see clearly that the magician criteria indicate the need for a {color{#4257b2}{Concave}} mirror with the object being placed between the mirror and the focal point }$
(b) To determine the position of the image $d_i$ we will use the magnifying equation:
$$
m=frac{h_i}{h_o}=-frac{d_i}{d_o}Rightarrow d_i=-frac{h_id_o}{h_o}=boxed{-16.4m}
$$
tt{(a)Concave mirror,(b) $d_i=-16.4m$}
$$
tt{The reflecting globe can be treated as a convex mirror at every section of it, therefore we can use the relation between the radius of curvature $R=frac{D}{2}$
and the focal length $f$ of a convex mirror: }
$$
$$
f=-frac{R}{2}=-frac{D}{4}=-4.5cm
$$
(a) Using the mirror equation we can determine the position of the image $d_i$:
$$
frac{1}{f}=frac{1}{d_i}frac{1}{d_o}Rightarrow frac{1}{d_i}=frac{1}{f}-frac{1}{d_i}=frac{d_o-f}{d_of}
$$
$$
Rightarrow d_i=frac{d_of}{d_o-f}= frac{3.6(-0.045)}{3.6+0.045}=-0.044m=boxed{-4.4cm}
$$
(b) We will use the magnifying equation to determine the height of the image $h_i$
$$
m=frac{h_i}{h_o}=-frac{d_i}{d_o}Rightarrow h_i=-frac{h_od_i}{d_o}=-frac{1600*(-4.4)}{3600}=boxed{1.95cm}
$$
tt{(a)$d_i=-4.4cm$,(b)$h_i=1.95cm$}
$$
(c) We solve the mirror equation for $f$:
$$
frac{1}{f}=frac{1}{d_o}+frac{1}{d_i}=frac{d_i+d_o}{d_id_o}
$$
$$
Rightarrow f=frac{d_id_o}{d_i+d_o}=frac{1.8*(-3.5)}{-3.5+1.8}=boxed{3.7m}
$$
tt{(a) $m=19$,(b) upright,(c) $f=3.7m$}
$$
tt{(a) The mirror equation states: $$frac{1}{f}=frac{1}{d_o}+frac{1}{d_i}$$
We will solve the mirror equatin for the position of the arstronomer’s image $d_i$: }
$$
$$
frac{1}{d_i}=frac{1}{f}-frac{1}{d_o}=frac{d_o-f}{d_of}Rightarrow d_i=frac{fd_o}{d_o-f}
$$
We know the mirror is concave therefore $f>0$
$$
Rightarrow d_i=frac{16.9*20}{20-16.9}=boxed{109m}
$$
$d_i>0Rightarrow$ The image is $text{color{#4257b2}{in front}}$ of the mirror.
(b) The image is $text{color{#4257b2}{real}}$ since $d_i>0$ and the image is formed in front of the mirror.`
(c) The magnification equation state:
$$
m=-frac{d_i}{d_o}=-frac{109}{20}=boxed{-5.45}
$$
tt{(a) $d_i=109m$,in front of the mirror (b)The image is real(c)$m=-5.45$}
$$
tt{(a) We know that the virtual image height $h_i$ is 3 times that of the real object $h_o$, therefore we can determine the magnifying equation as: }
$$
$$
m=frac{h_i}{h_o}=3
$$
We then can deduce the $d_i$ the position of the image using also the magnifying equation:
$$
m=-frac{d_i}{d_o}Rightarrow d_i=-d_om=-22*3=boxed{-66cm}
$$
The image is $text{color{#4257b2}{66cm behind}}$ the mirror.
(b) Using the mirror equation we can determine the focal length $f$ of the mirror:
$$
frac{1}{f}=frac{1}{d_o}+frac{1}{d_i}=frac{d_i+d_o}{d_od_i}
$$
$$
Rightarrow f= frac{d_id_o}{d_i+d_o}=frac{(-66)*22}{-66+22}=boxed{33cm}
$$
tt{(a)The image is 66cm behind the mirror,(b)$f=33cm$}
$$
tt{The magnifying equation state:}
$$
$$
m=frac{h_i}{h_o}=-frac{d_i}{d_o}
$$
We first calculate the magnifying factor $m$ using the postion of the tree $d_o$ and its image $d_i$:
$$
m=-frac{d_i}{d_o}=-frac{0.07}{21}=-3.33*10^{-3}
$$
We then use the second part of the formula to determine the tree real height $h_o$:
$$
m=frac{h_i}{h_o}Rightarrow h_o=frac{h_i}{m}=frac{-0.035}{-3.33*10^{-3}}=boxed{10.5m}
$$
h_o=10.5text{m}
$$
tt{The magnifying equation states:}
$$
$$
m=-frac{d_i}{d_o}
$$
We know that the magnifying factor is 2 therefore we can calculate the image position$d_i$:
$$
d_i=-d_om=-25*2=-50cm
$$
Using the mirror equation we can calculate the focal length $f$ of the mirror:
$$
frac{1}{f}=frac{1}{d_o}+frac{1}{d_i}=frac{d_o+d_i}{d_od_i}
$$
$$
Rightarrow f=frac{d_od_i}{d_i+d_o}=frac{25*(-50)}{-50+25}=50cm
$$
We finally use the relation between the focal length$f$ and the radius of curvature $R$:
$$
f=frac{R}{2}Rightarrow R=2f=2*50=boxed{100cm}
$$
f=100cm
$$
The Law of reflection states
$$
theta_i=theta_r
$$
therefore if the incident beam is normal to the mirror’s surface $theta_i=0$ then the reflection angle $theta_r$ will also be equal to zero and the reflected beam will be also norma to the mirror’s surface.
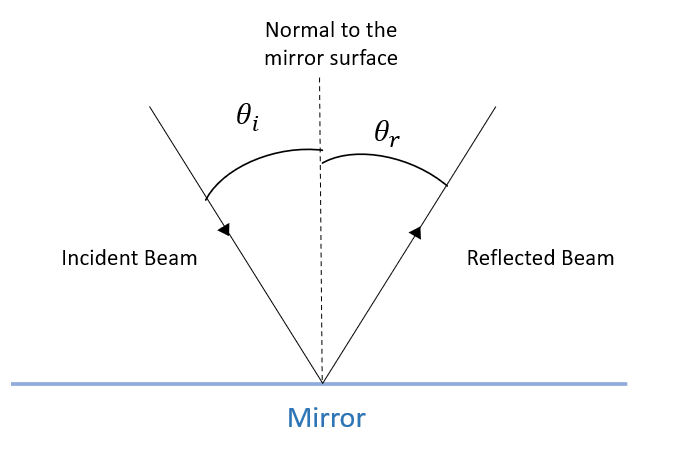
theta_r=0
$$
tt{First we draw the object(Black) and its image (Dashed black) using the Principal Rays then we position the object a little further to the left (Red) and repeat the same process to obtain the new image (Dashed red) \
$Rightarrow$ We can see that moving the object to the left results in moving the image to the right.}
$$
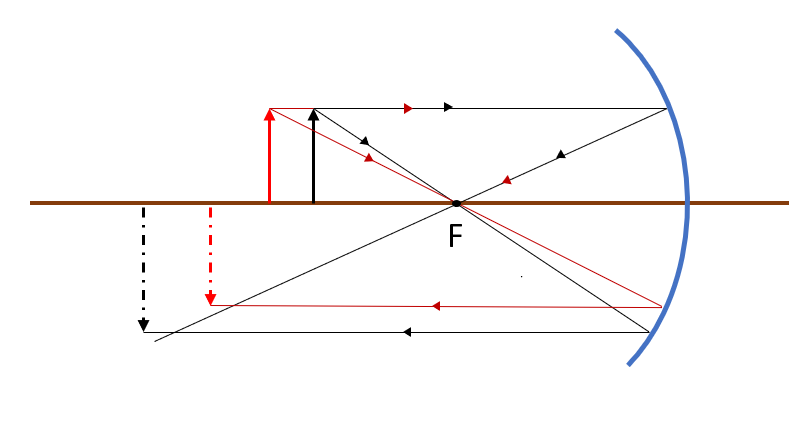
tt{Right}
$$
tt{First we draw the object (Red), using the principal Rays we determine the image (dashed Red), then we move the object a little more to the mirror (Black) and repeat the same process to obtain the new image(dashed Black)}
$$
$Rightarrow$ We can notice that as the object get closer to the mirror, the image $text{color{#4257b2}{increase}}$ in size
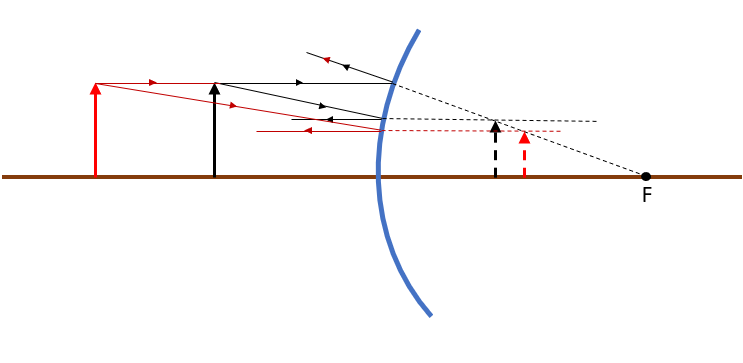
tt{increase}
$$
$text{color{#4257b2}{Plane mirror:}}$ For this type of mirrors the distance of the object to the mirror is always equal to the distance of the virtual image to the mirror$Rightarrow d_i=-d_o$, we can see that the relation between the two distances is clearly linear therefore the proposed Graph can not describe a plane mirror
The mirror equation states:
$$
frac{1}{f}=frac{1}{d_i}+frac{1}{d_o}Rightarrow frac{1}{d_i}=frac{1}{f}-frac{1}{d_o}=frac{d_o-f}{d_of}
$$
$$
Rightarrow d_i=frac{d_of}{d_o-f}
$$
$text{color{#4257b2}{Concave mirror:}}$ For this type of mirrors, the focal length $f$ is always positive therefore the sign of the image distance $d_i$ can vary depending on the sign of the term $d_o-f$,the proposed Graph can not describe a concave mirror.
$text{color{#4257b2}{Convex mirror:}}$For this type of mirrors, the focal length $f$ is always negative therefore the sign of the image distance $d_i$ is always negative.therefore the proposed Graph describes well a convex mirror.
tt{convex mirror}
$$
tt{The Real object sits beyond the center of curvature $C$, Based on {color{#4257b2}{Table 16.1}}The image of this object should be inverted, reduced, and real. \
By examining the Figure we can deduce that only image (2) fulfill the criteria}
$$
tt{image (2)}
$$
tt{The relation between the focal length $f$ and the center of curvature $R$ for a convex mirror yields:}
$$
$$
f=-frac{R}{2}Rightarrow f=-frac{D}{4}=-11.25cm
$$
We can now use the Mirror equation to determine the the position of the image $d_i$
$$
frac{1}{f}=frac{1}{d_o}+frac{1}{d_i}Rightarrow frac{1}{d_i}=frac{1}{f}-frac{1}{d_o}=frac{d_o-f}{d_of}
$$
$$
Rightarrow d_i=frac{d_of}{d_o-f}=frac{0.55*(-0.1125)}{0.55+0.1125}=-0.093m=-9.3cm
$$
It remains to determine the image size using the magnifying equation:
$$
m=frac{h_i}{h_o}=-frac{d_i}{d_o}Rightarrow h_i=-frac{d_ih_o}{d_o}=-frac{(-9.3)*170}{55}=boxed{29cm}
$$
h_i=29cm
$$
The object is sitting at the center of curvature of the mirror therefore $d_o=R$
We also have the relation between the Radius and the focal length of a concave mirror: $f=frac{R}{2}$
We can deduce that : $d_o=R=2f$
To determine the characteristics of the image we have to find the image position $d_i$ and the size $h_i$.
The mirror equation states:
$$
frac{1}{f}=frac{1}{d_o}+frac{1}{d_i}Rightarrow frac{1}{d_i}=frac{1}{f}-frac{1}{d_o}=frac{d_o-f}{d_of}
$$
$$
Rightarrow d_i=frac{d_of}{d_o-f}=frac{(2f)f}{(2f)-f}=frac{2f^2}{f}=2f
$$
$$
Rightarrow d_i=d_o>0
$$
(a) The image is Real since $d_i>0$
(b) The image is also located at the center of curvature $d_i=d_o=2f=R$
We then use the magnifying equation to determine the type of image:
$$
m=-frac{d_i}{d_o}=-frac{d_o}{d_o}=-1
$$
(c) $m<1$, The image is inverted
(d) the magnification is 1 to 1 scale. (no magnification).
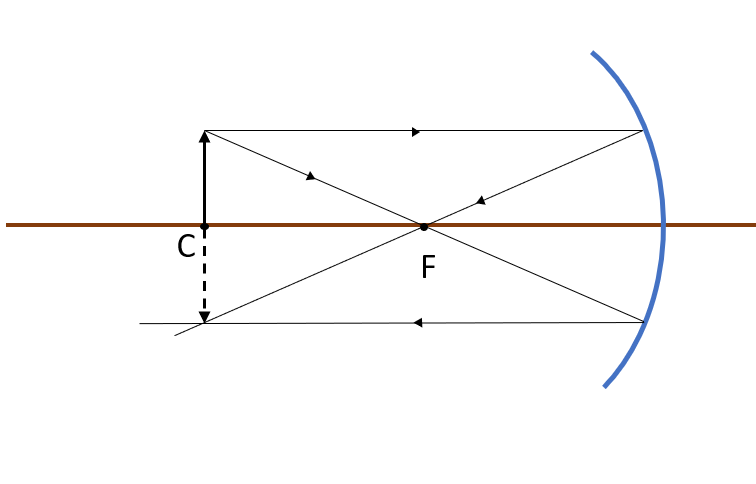
tt{(a)Real,(b)At the center of the curvature,(c)inverted,(d)$m=-1$}
$$
tt{The Mirror equation states that:}
$$
$$
frac{1}{f}=frac{1}{d_o}+frac{1}{d_i}Rightarrow frac{1}{d_i}=frac{1}{f}-frac{1}{d_o}
$$
For a flat mirror $flongrightarrow infty$ since we can consider it as a curved mirror with an infinite radius of curvature
$$
lim_{flongrightarrowinfty}{frac{1}{f}}=0.
$$
The mirror equation becomes $frac{1}{d_i}=-frac{1}{d_o}Rightarrow d_i=-d_o$
d_i=-d_o
$$
$d_o=12.cm$
$h_o=3.5cm$
$f=5cm$
}
The mirror equation states:
$$
frac{1}{f}=frac{1}{d_o}+frac{1}{d_i}Rightarrow frac{1}{d_i}=frac{1}{f}-frac{1}{d_o}=frac{d_o-f}{d_of}
$$
$$
Rightarrow d_i=frac{d_of}{d_o-f}=frac{5*12}{12-5}=boxed{8.6cm}
$$
The magnifying equation states:
$$
m=frac{h_i}{h_o}=-frac{d_i}{d_o}Rightarrow h_i=-frac{d_ih_o}{d_o}=-frac{8.6*3.5}{12}=boxed{-2.5cm}
$$
tt{$d_i=8.6cm$ and $h_i=-2.5cm$}
$$
Let’s denote $N$ the number of reflection occurring on both mirrors surfaces:
$$
N=frac{x}{168}
$$
if$xuparrow$ then $Ndownarrow Rightarrow$ The number of reflections $text{color{#4257b2}{decresases}}$.
(b)
$$
tan15^o=frac{x}{125}Rightarrow x=125tan{15^o}=33.5 cm
$$
$$
N=frac{x}{168}=frac{33.5}{168}=5
$$
The light will be reflected 5 times before exiting the mirror corridor.
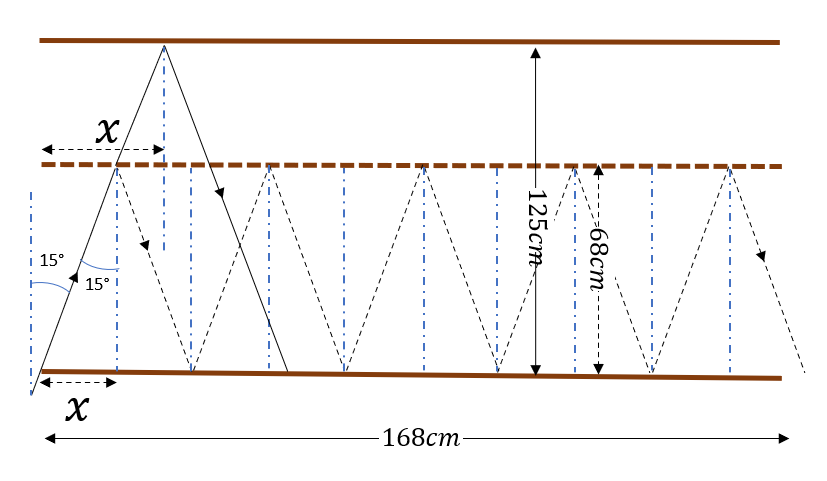
tt{(a)increase,(b)5}
$$
The magnification equation states:
$$
m=frac{abs{h_i}}{h_o}=-frac{d_i}{d_o}Rightarrow d_i=-frac{abs{h_i}d_o}{h_o}
$$
$$
begin{align*}
d_i=-frac{(2h_o)d_o}{h_o} & text{ or } d_i=-frac{(-2h_o)d_o}{h_o}\
d_i=-2d_o & text{ or } d_i=2d_o
end{align*}
$$
On the other hand, we can determine the focal length by using its relation to the center of Curvature:
$$
f=frac{R}{2}=16cm
$$
Finally to determine the numerical value of the image location $d_i$, we resort to the mirror equation:
$$
frac{1}{f}=frac{1}{d_o}+frac{1}{d_i}Rightarrow frac{1}{d_o}=frac{1}{f}-frac{1}{d_i}=frac{d_i-f}{d_if}
$$
$$
Rightarrow d_o=frac{d_if}{d_i-f}
$$
$$
begin{align*}
d_o=frac{2d_of}{2d_o-f} & text{ or } d_o=frac{-2d_of}{-2d_o-f} \
2d_o-f=2f & text{ or } 2d_o+f=2f\
d_o=frac{3}{2}f & text{ or } d_o=frac{1}{2}f \
d_o=boxed{14cm} & text{ or } d_o=boxed{8cm}
end{align*}
$$
(b) To determine if the image is real or virtual we need to evaluate the sign of $d_i$, Based on the mirror equation, the general form of $d_i$ :
$$
d_i=frac{d_of}{d_o-f}
$$
$$
begin{align*}
text{for }d_o=24cm & text{ for }d_o=8cm \
d_i=frac{24*16}{24-16} & text{ } d_i=frac{8*16}{8-16} \
d_i=48cm & text{ } d_i=-16cm\
d_i>0text{ Real Image } & d_i<0text{ Virtual Image }
end{align*}
$$
tt{(a) $d_o$=[24cm,8cm];(b) for 24cm the image is real, for 8cm the image is virtual}
$$
$$
frac{1}{f}=frac{1}{d_o}+frac{1}{d_i}Rightarrow frac{1}{d_i}=frac{1}{f}-frac{1}{d_o}=frac{d_o-f}{d_of}
$$
$$
Rightarrow d_i=frac{d_of}{d_o-f}=frac{2.2*(-0.75)}{2.2+0.75}=boxed{-0.56m}
$$
(b)To determine if the image is upright or inverted we need to examine the magnification factor sign:
$$
m=-frac{d_i}{d_o}=frac{0.56}{2.2}=0.25
$$
$m>0Rightarrow$ The image is $text{color{#4257b2}{Upright}}$
(c) Using the magnification equation we can determine the image size $h_i$:
$$
m=frac{h_i}{h_o}Rightarrow h_i=mh_o=boxed{0.43m}
$$
tt{(a)$d_i=-0.56m$,(b)The image is upright,(c) $m=0.43m$}
$$
Based on Fig. 16.34, we obtain the following dimensions:
– Height of the eys from the ground: 1.6 m
– Mirror and eyes distance: 0.5 m
– Height of the mirror: 0.32 m
– Distance of the build from the person: 95 m
– Lowest point the person can see on the building above the ground: 19.6 m
(a) To find the height of the mirror such that the lowest point the person can see on the build is 19.6 m above the ground, we need to determine the vertical and horizontal distance covered by the line of sight of the person.
(b) To find the highest point on the building the person can see, we need to determine the horizontal short segment of the line of sight of 0.50 m and the total vertical distance covered by both segments of the line of sight.
The vertical distance covered by the line of sight of the person is the difference between the lowest point the person can see on the building above the ground and height of the eys from the ground, we have
$$
begin{aligned}
19.6;text{m} – 1.6;text{m} = 18.0;text{m}
end{aligned}
$$
$$
begin{aligned}
95;text{m} – 2(0.5);text{m} = 96;text{m}
end{aligned}
$$
$$
begin{aligned}
h_1 &= 19.6;text{m} – (18.0;text{m})left(frac{95;text{m}+0.5;text{m}}{96;text{m}}right) \ &= 1.694;text{m}text{ or }boxed{1.7;text{m}}
end{aligned}
$$
$$
begin{aligned}
1.694;text{m} + 0.32;text{m} – 1.6;text{m} = 0.414;text{m}
end{aligned}
$$
$$
begin{aligned}
h_2 &= (0.414;text{m})left(frac{96;text{m}}{0.5;text{m}}right) \ &= 79.5;text{m}
end{aligned}
$$
$$
begin{aligned}
79.5;text{m} + 1.6;text{m} = boxed{81.1;text{m}}
end{aligned}
$$
(b) $h_2 = 81.1$ m
tt{(a)We know that the image is real therefore $d_i>0$,whereas $d_o>0$ always, consequentially we can determine the sign of the magnification factor:}
$$
$$
m=-frac{d_i}{d_o}<0 Rightarrow m=-3
$$
Now we can calculate the position of the image:
$$
d_i=md_o=(-3)32=boxed{66cm}
$$
(b) using the mirror equation we can determine the focal length $f$:
$$
frac{1}{f}=frac{1}{d_o}+frac{1}{d_i}Rightarrow frac{1}{f}=frac{d_i+d_o}{d_id_o}
$$
$$
Rightarrow f= frac{d_od_i}{d_o+d_i}=frac{22*66}{22+66}=boxed{16.5cm}
$$
tt{(a)$d_i=66cm$,(b)$f=16.5cm$}
$$
tt{(a)The image is virtual thefore $d_i0 , m=frac{1}{4}
$$
Now we can calculate the position of the image as :
$$
d_i=-md_o=-frac{1}{4}32=boxed{-8cm}
$$
The image is 8cm behind the mirror.
(b) Using the mirror equation we can calculta the focal length:
$$
frac{1}{f}=frac{1}{d_o}+frac{1}{d_i}=frac{d_i+d_o}{d_od_i}
$$
$$
f=frac{d_od_i}{d_i+d_o}=frac{32*(-8)}{32-8}=boxed{-10.67cm}
$$
tt{(a) $d_i=-8cm$,(b)$f=-10.67cm$}
$$
tt{(a) The mirror is convex therfore the image is always virtual and positioned behind the mirror $d_i0
$$
Since $m>0$, the image formed is $text{color{#4257b2}{upright.}}$
(b) Using the magnification equation we can determine the exact position of the image $d_i$:
$$
m=frac{h_i}{h_o}=-frac{d_i}{d_o} Rightarrow di=-frac{h_id_o}{h_o}=-frac{16.25*520}{170}=-49.7cm
$$
Now we can determine the focal length $f$ using the mirror equation:
$$
frac{1}{f}=frac{1}{d_o}+frac{1}{d_i}=frac{d_i+d_o}{d_od_i}
$$
$$
f=frac{d_od_i}{d_i+d_o}=frac{520*(-49.7)}{520-49.7}=-54.95cm
$$
Finally we can determine the Radius of curvature of the mirror:
$$
f=-frac{R}{2}Rightarrow R=-2f=-2*54.95=boxed{110cm}
$$
tt{(a) The image is upright,(b) $f=110cm$}
$$
tt{Mirrors have a very smooth opaque surface that is able to reflect incident light from objects and redirect it elsewhere, if this light reaches our retinas then we will see the mirror image of the object.\
The mirror image position and size can vary based on the type of mirror but it can always be determined thanks to the magnification equation:
$$m=frac{h_i}{h_o}=-frac{d_i}{d_o}$$
An image can be smaller in size than the original object $h_ih_o$.\
It can also be upright $m>0$ or inversed $m<0$ \
Both of these characteristics are an outcome based on the original position of the object $d_o$ and the focal length of the mirror $f$, the combination of different values of $d_o$ and $f$ will also result in a variable position of the image $d_i$, All of the three variables are linked through the mirror equation:
$$frac{1}{f}=frac{1}{d_o}+frac{1}{d_i}$$
}
$$
tt{The mirror image parameters vary according to the magnification and mirror equations}
$$
$text{color{#4257b2}{ Plane mirror}}$: in this case, the rays are perpendicular to the mirror surface and will be reflected in the same direction as the incident rays without any further consequences.
$text{color{#4257b2}{ Convex mirror}}$: The rays will converge to the focal point of the mirror, for a convex mirror the focal point is behind the mirror therefore in reality the rays will be reflected and dispersed as depicted in Figure 16.21
$text{color{#4257b2}{Concave mirror}}$: The rays will converge to the focal point of the mirror, for a concave mirror the focal point is in front of the mirror therefore the rays will be reflected and concentrated in the focal point as depicted in Figure 16.20, every object located in the focal point will absorb a large amount of energy from light and turn it into heat, consequentially raising its tempreature
tt{(B)}
$$
Therefore the focal length of the mirror is $f=frac{R}{2}=frac{160}{2}=80$ m.
Since the incoming sun light is parallel, it will be focused at the focal point of the mirror. Hence here the light will be focused at 80 m.
tt{First we need to determine the focal length $f$ of the mirror, by using the relation between $f$ and the radius of curvature $R$:}
$$
$$
f=frac{R}{2}=frac{160}{2}=80m
$$
Now we can determine the distance of the image $d_i$ using the mirror equation :
$$
frac{1}{f}=frac{1}{d_o}+frac{1}{d_i}Rightarrow frac{1}{d_i}=frac{1}{f}-frac{1}{d_o}=frac{d_o-f}{d_of}
$$
$$
Rightarrow d_i=frac{d_of}{d_o-f}=frac{25*80}{25-80}=boxed{-36.4m}
$$
d_i=-36.4m
$$
tt{We can use a Ray Diagram to determine the outcome if the person (Black arrow) decides to move closer to the mirror (Red arrow).\ Important information to take into consideration is that the person in both positions sits within the focal length $f$ of the mirror $Rightarrow d_o<f$}
$$
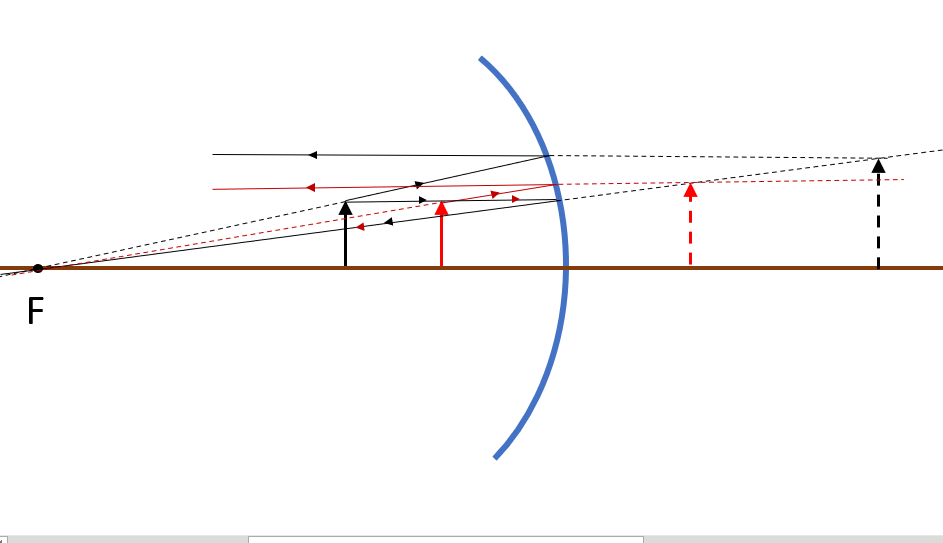
tt{(A)The image moves closer to the person}
$$

