
All Solutions
Page 180: Assessment
For this part, the force acting on an object doubles. The mass is constant. We find out what happens to the acceleration.
$$
begin{align*}
F &= ma \
implies a &= frac{F}{m} \
a &propto F
end{align*}
$$
The acceleration is directly proportional to the force applied. Since the force doubles, the acceleration also $textbf{doubles}$.
For this part, the mass of the object doubles, but the force is kept constant. We find what happens to the acceleration.
$$
begin{align*}
F &= ma \
implies a &= frac{F}{m} \
a &propto frac{1}{m}
end{align*}
$$
The acceleration and mass are inversely proportional. Since the mass doubles, the acceleration must $textbf{half}$.
Hence, the silverware stays in place while the tablecloth rushes beneath it.
From Newton’s 3rd law, both the small car and large truck would apply the same magnitude of force on one another. The acceleration and mass (with constant $F$) are related by
$$
begin{align*}
F &= ma \
implies a &= frac{F}{m} \
a &propto frac{1}{m}
end{align*}
$$
The acceleration and mass are inversely proportional. The object with more acceleration must have less mass. Hence, the acceleration of the car is $textbf{greater}$ than the acceleration of the truck.
Based on the previous part, the best explanation would be $textbf{B.}$ “both vehicles experience the same force; therefore, the lightweight car experiences the greater acceleration.
$$
begin{align*}
F &= ma\\
Rightarrow a & = dfrac{F}{m}
end{align*}
$$
So the acceleration is inversely proportional to the mass of the object for constant force.
Thus, for the same force, since the earth has massive mass (away larger than that of a man), so its acceleration is very small to be noticable.
$$
begin{gather*}
w = m_mg = (70.0text{ kg})cdot (9.81text{ m/s}^2) = 686.7text{ N}
end{gather*}
$$
This is the force exerted by the earth on the man; So, according to $textbf{Newton’s third law}$, the man is also exerting a force on the earth equal in magnitude and opposite in direction to its weight, $F= w$.
And we know that the mass of the earth is $M_E = 5.97times 10^{24}$ kg.
So, form $textbf{Newton’s second law}$, the acceleration of the earth is:
$$
begin{gather*}
a = dfrac{686.7text{ N}}{ 5.97times 10^{24}text{ kg}} = 1.15times 10^{-22}text{ m/s}^2
end{gather*}
$$
This acceleration is very small to be noticed.
$$
begin{align*}
F &= ma\\
Rightarrow a & = dfrac{F}{m}
end{align*}
$$
Since the three bucks have the same mass and the forces acting on them are equal, so, according to $textbf{Newton’s second law}$, all have the same acceleration.
$$
begin{gather*}
large boxed{a_A = a_B = a_C}
end{gather*}
$$
And the velocity of any buck at any moment does not affect the acceleration.
a_A = a_B = a_C
$$
From $textbf{Newton’s second law}$ for multiple forces, the net force on an object is equal to its mass times its acceleration:
$$
begin{gather*}
sum vec{textbf{F}} = mvec{textbf{a}}tag{1}
end{gather*}
$$
The mass of the golf cart is $m = 540$ kg and its acceleration is $a = 2.50text{ m/s}^2$.
We simply plug our values for $m$ and $a$ into equation (1), so we get the net force that must act on the golf cart:
$$
begin{gather*}
sum F = (540text{ kg}) cdot (2.50text{ m/s}^2) = 1350text{ N}\\
therefore quad large boxed{sum F = 1350text{ N}}
end{gather*}
$$
sum F = 1350text{ N}
$$
From Newton’s second law for multiple forces, the net force on an object is equal to its mass times its acceleration:
$$
begin{align*}
sum overrightarrow{mathbf{F}}=m overrightarrow{mathbf{a}} tag1
end{align*}$$
The net force acting on a backpack is $sum F=23.0 mathrm{~N}$ and its acceleration is $a=3.80 mathrm{~m} / mathrm{s}^{2}$.
We simply plug our values for $sum F$ and $a$ into equation (1) and evaluate for $m$, so we get the mass of the backpack:
$$
begin{align*}
begin{gathered}
m=frac{sum F}{a}=frac{23.0 mathrm{~N}}{3.80 mathrm{~m} / mathrm{s}^{2}}=6.05 mathrm{~kg} \
therefore quad mapprox6 mathrm{~kg}
end{gathered}
end{align*}$$
From $textbf{Newton’s second law}$ for multiple forces, the net force on an object is equal to its mass times its acceleration:
$$
begin{gather*}
sum vec{textbf{F}} = mvec{textbf{a}}tag{1}
end{gather*}
$$
The mass of the rainbow trout is $m = 1.30$ N and the net force on it is $sum F = 3.40text{ N}$.
We simply plug our values for $sum F$ and $m$ into equation (1) and evaluate for $a$, so we get the acceleration of the rainbow trout:
$$
begin{gather*}
a = dfrac{sum F}{m} = dfrac{3.40text{ N}}{1.30text{ kg}} = 2.62text{ m/s}^2\\
therefore quad large boxed{a = 2.62text{ m/s}^2}
end{gather*}
$$
a = 2.62text{ m/s}^2
$$
From $textbf{Newton’s second law}$ for multiple forces, the net force on an object is equal to its mass times its acceleration:
$$
begin{gather*}
sum vec{textbf{F}} = mvec{textbf{a}}tag{1}
end{gather*}
$$
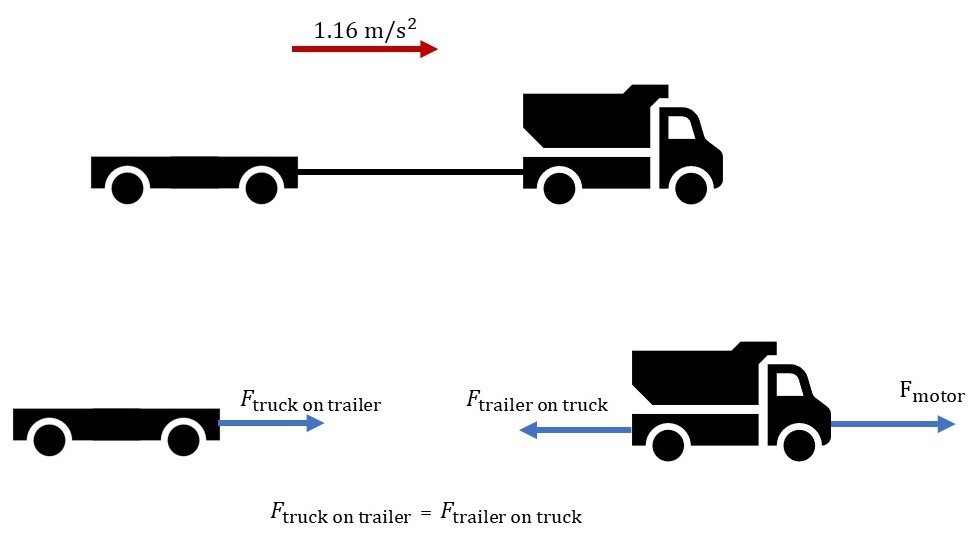
The mass of the trailer is $m_text{trailer} = 620$ kg and the acceleration of the system (truck and trailer) is $a = 1.16text{ m/s}^2$.
Assuming there is no friction between the trailer and the ground, the net force on the trailer is due to the truck.
So, we simply plug our values for $m_text{trailer}$ and $a$ into equation (1), so we get the force exerted by the truck on the trailer (net force):
$$
begin{gather*}
F = (620text{ kg}) cdot (1.16text{ m/s}^2) = 719.2text{ N}\\
therefore quad large boxed{F = 719.2text{ N}}
end{gather*}
$$
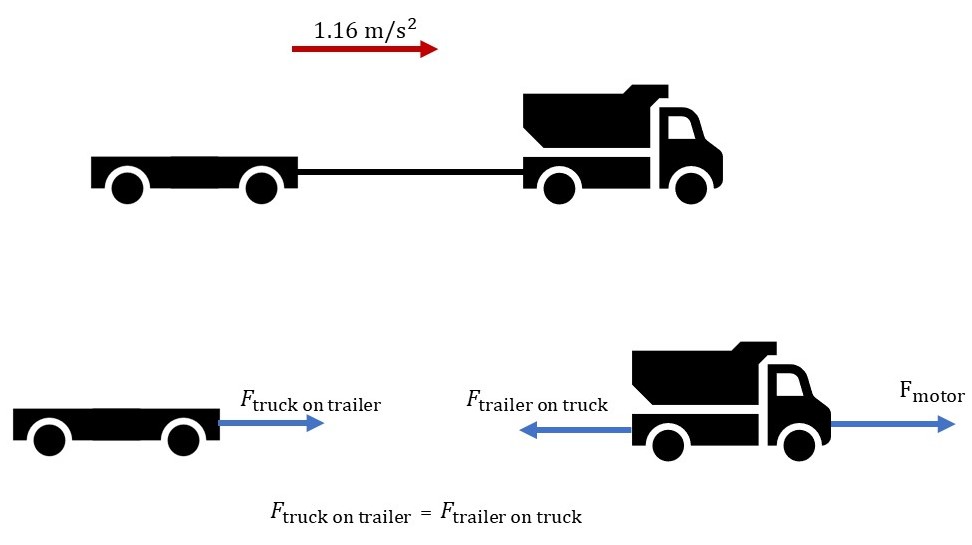
From $textbf{Newton’s second law}$ for multiple forces, the net force on an object is equal to its mass times its acceleration:
$$
begin{gather*}
sum vec{textbf{F}} = mvec{textbf{a}}tag{1}
end{gather*}
$$
The mass of the trailer is $m_text{truck} = 1800$ kg and the acceleration of the system (truck and trailer) is $a = 1.16text{ m/s}^2$.
Assuming there is no friction between the trailer and the ground, there are two forces exerted on the truck, one is the applied force by the motor pushing it forward and the other is the force exerted by the trailer pulling it back.
We simply plug our values for $m_text{truck}$ and $a$ into equation (1), so we get the net force exerted on the truck:
$$
begin{gather*}
sum F = (1800text{ kg}) cdot (1.16text{ m/s}^2) = 2088text{ N}\\
therefore quad large boxed{sum F = 2088text{ N}}
end{gather*}
$$
– For every action force acting on an object, there is a reaction force acting on a different object.
– The action and reaction forces are equal in magnitude and opposite in direction.
Thus, according to $textbf{Newton’s third law}$, the force experienced by the child $textbf{the same as}$ the force experienced by the parent.
$$
begin{gather*}
F = ma
end{gather*}
$$
Rearranging this equation, we get:
$$
begin{gather*}
a = dfrac{F}{m}
end{gather*}
$$
So, with constant force, the acceleration decreases when increasing the mass.
Since both the parent and the child experiences the same force, and the mass of the parent is larger than that of the child ($91.0text{ kg} > 21.0text{ kg}$),
thus, the acceleration of the child is $textbf{more than}$ the acceleration of the parent.
(b) More than.
$textbf{Newton’s second law}$ states that, the force exerted on an object is equal to its mass times its acceleration.
$$
begin{gather*}
F = matag{1}
end{gather*}
$$
$textbf{Newton’s third law}$ states that:
– For every action force acting on an object, there is a reaction force acting on a different object.
– The action and reaction forces are equal in magnitude and opposite in direction.
The mass of the parent is $m_p = 91.0text{ kg}$, the mass of the child is $m_c = 21.0text{ kg}$ and the acceleration of the child is $a_c = 0.310text{ m/s}^2$.
First, we plug our values for $m_c$ and $a_c$ into equation (1), so we get the force experienced by the child:
$$
begin{gather*}
F_c = (21.0text{ kg}) cdot (0.310text{ m/s}^2) = 6.51text{ N}
end{gather*}
$$
According to $textbf{Newton’s third law}$, the force experienced by the parent is the same as the force experienced by the child.
$$
begin{gather*}
F_p = F_c = 6.51text{ N}
end{gather*}
$$
Now, we plug our values for $F_p$ and $m_p$ into equation (1) and evaluate for $a_p$, so we get the acceleration of the parent:
$$
begin{gather*}
a_p = dfrac{F_p}{m_p} = dfrac{6.51text{ N}}{91.0text{ N}} = 0.0715text{ m/s}^2\\
therefore quad large boxed{a_p = 0.0715text{ m/s}^2}
end{gather*}
$$
a_p = 0.0715text{ m/s}^2
$$
From $textbf{Newton’s second law}$ for single force, the force exerted on an object is equal to its mass times its acceleration:
$$
begin{gather*}
F = matag{1}
end{gather*}
$$
From the $textbf{definition of average acceleration}$, the average acceleration is the change in velocity divided by the change in time:
$$
begin{gather*}
a = dfrac{v_f – v_i}{Delta t}tag{2}
end{gather*}
$$
The average force exerted on the jet is $F = 9.35times 10^{5}$ N, its initial speed is $v_i = 0$, final speed is $v_f = 250$ km/h and the time interval of this speed up is $Delta t = 2.00$ s.
First, we convert the final speed from $textbf{km/h}$ to $textbf{m/s}$ as follows:
$$
begin{gather*}
v_f = (250text{ km/h}) left( dfrac{1000text{ m}}{1.0text{ km}} right) left( dfrac{1.0text{ h}}{3600text{ s}} right) = 69.4text{ m/s}
end{gather*}
$$
Next, we plug our values for $v_i$, $v_f$ and $Delta t$ into equation (2), so we get the average acceleration of the jet:
$$
begin{gather*}
a = dfrac{69.4text{ m/s} – 0}{2.00text{ s}} = 34.7text{ m/s}^2
end{gather*}
$$
Finally, we plug our values for $F$ and $a$ into equation (1) and evaluate for $m$, so we get the mass of the jet:
$$
begin{gather*}
m = dfrac{F}{a} = dfrac{9.35times 10^{5}text{ N}}{34.7text{ m/s}^2} = 26928text{ kg} \\
therefore quad large boxed{m = 26928text{ kg}}
end{gather*}
$$
m = 26928text{ kg}
$$
From $textbf{Newton’s second law}$ for multiple forces, the net force on an object is equal to its mass times its acceleration:
$$
begin{gather*}
sum vec{textbf{F}} = m vec{textbf{a}}tag{1}
end{gather*}
$$
The average acceleration is the change in velocity divided by the change in time:
$$
begin{gather*}
a = dfrac{v_f – v_i}{Delta t}tag{2}
end{gather*}
$$
From position-time kinematic equation, the relation between the change in position, initial speed, acceleration and time is given by:
$$
begin{gather*}
Delta x = v_i t + dfrac{1}{2}at^2tag{3}
end{gather*}
$$
The mass of the car is $m = 950$ kg, the time of the brake is $Delta t = 1.20$ s, the initial speed of the car is $v_i = 16.0$ m/s and the final speed is $v_f = 9.50$ m/s.
(a) First, we plug our values for $v_i$, $v_f$ and $Delta t$ into equation (2), so we get the average acceleration of the car during braking:
$$
begin{gather*}
a = dfrac{9.50text{ m/s} – 16.0text{ m/s}}{1.20text{ s}} = -5.42text{ m/s}^2
end{gather*}
$$
Now, we plug our values for $m$ and $a$ into equation (1), so we get the average force exerted on the car during braking:
$$
begin{gather*}
F = (950text{ kg}) cdot (-5.42text{ m/s}^2) = -5146text{ N}\\
therefore quad large boxed{F = -5146text{ N}}
end{gather*}
$$
(b) We simply plug our values for $v_i$, $t$ and $a$ into equation (3), so we get the distance traveled while braking:
$$
begin{gather*}
Delta x = (16.0text{ m/s})cdot (1.20text{ s}) + dfrac{1}{2} (-5.42text{ m/s}^2) (1.20text{ s})^2\\
therefore quad large boxed{Delta x = 15.3text{ m}}
end{gather*}
$$
(b) $Delta x = 15.3$ m
From $textbf{Newton’s second law}$ for multiple forces, the net force on an object is equal to its mass times its acceleration:
$$
begin{gather*}
sum vec{textbf{F}} = m vec{textbf{a}}tag{1}
end{gather*}
$$
From velocity-position kinematic equation, the relation between the change in position, initial speed, final speed and acceleration is given by:
$$
begin{gather*}
v_f^2 = v_i^2 + 2aDelta xtag{2}
end{gather*}
$$
The weight of the firefighter is $w = 782$ kg, his initial speed is $v_i = 0$ and his final speed is $v_f = 4.20$ m/s and the distance he slides is $d = 3.30$ m.
We take upward as the positive direction.
Since the firefighter slides down, so the change in his position is $Delta y = -d = -3.30$ m and his final velocity is $vec{v}_f = -4.20$ m/s.
Now, we plug our values for $v_i$, $vec{v}_f$ and $Delta y$ into equation (2) and evaluate for $vec{a}$, so we get his acceleration:
$$
begin{align*}
(-4.20text{ m/s})^2 &= (0)^2 + 2 (-3.30text{ m}) vec{a}\\
vec{a} &= dfrac{(-4.20text{ m/s})^2}{2 (-3.30text{ m})} = -2.67
end{align*}
$$
Then, we calculate the mass of the firefighter as follows:
$$
begin{gather*}
m = dfrac{w}{g} = dfrac{782text{ N}}{9.81text{ m/s}^2} = 79.7text{ kg}
end{gather*}
$$
By applying $textbf{Newton’s second law}$ in the $y$-direction, we get:
$$
begin{align*}
sum vec{textbf{F}}_y = vec{F}_text{pole} – w &= mvec{a}\\
vec{F}_text{pole} &= mvec{a} + w
end{align*}
$$
Now, we plug our values for $m$, $vec{a}$ and $w$, so we get the average force exerted by the pole on the firefighter:
$$
begin{gather*}
vec{F}_text{pole} = (79.7text{ kg}) cdot (-2.67text{ m/s}) + 782text{ N} = 569text{ N}\\
therefore quad large boxed{vec{F}_{text{pole}} = 569text{ N}}
end{gather*}
$$
From $textbf{Newton’s second law}$ for multiple forces, the net force on an object is equal to its mass times its acceleration:
$$
begin{gather*}
sum vec{textbf{F}} = m vec{textbf{a}}tag{1}
end{gather*}
$$
Let $F_1$ be the magnitude of the first exerted force, and $F_2$ is the magnitude of the second exerted force (the required forces) where $F_1 > F_2$.
Now, in the case when the two forces are in the same direction, we apply $textbf{Newton’s second law}$ to the object, so we get:
$$
begin{align*}
sum vec{textbf{F}} = F_1 + F_2 = m a_1tag{2}
end{align*}
$$
Then, in the case when they are in opposite direction, the direction of the acceleration will be in the same direction as the larger force;
Thus, we apply $textbf{Newton’s second law}$ to the object, so we get:
$$
begin{align*}
sum vec{textbf{F}} = F_1 – F_2 = ma_2tag{3}
end{align*}
$$
By adding equation (3) to equaion (2), we get:
$$
begin{gather*}
2F_1 = ma_1 + m a_2\\
therefore quad large boxed{F_1 = dfrac{m}{2} (a_1 + a_2)}
end{gather*}
$$
Now, we subtract equation (3) from equation (2), so we get:
$$
begin{gather*}
2F_2 = ma_1 – ma_2\\
therefore quad large boxed{F_2 = dfrac{m}{2} (a_1 – a_2)}
end{gather*}
$$
$F_2 = dfrac{m}{2} (a_1 – a_2)$
Since the weight of an object is the magnitude of the gravitational force acting on the object, and any object is falling under the gravitational force has an acceleration of $g$,
thus the weight (gravitational force) of any object of mass $m$ is equal to the mass $m$ times the gravitational acceleration $g$, $mg$.
The free-body diagrams are used for applying $textbf{Newton’s laws}$ by choosing a coordinate system and each force is resolved into components.
At this point Newton’s laws can be applied to each coordinate direction separately.
It is used for applying $textbf{Newton’s laws}$.
textbf{Upward}
$$
If the elevator is accelerating upwards, then the force causing the acceleration, ADDS to the force of gravity. So our apparent weight will increase.
If it is accelerating downwards, then the force causing the acceleration is OPPOSING the force of gravity, so our apparent weight goes down. If we were standing on a set of bathroom scales in the elevator, and it fell with an acceleration equal to g, then we would be weightless
$$
begin{align*}
F = kx\\
Rightarrow qquad x &= dfrac{F}{k}
end{align*}
$$
Where $k$ is the spring constant.
Thus, if the exerted force exerted is doubled, the distance of the stretch increases by a factor of $2$.
If she tightens her grip so that the force exerted on her by the rope equals her weight, by applying $textbf{Newton’s second law}$, we get:
$$
begin{align*}
sum F_y = F – mg &= ma\\
ma &= F – mg = mg – mg = 0\\
a & = 0
end{align*}
$$
Thus, she will continue sliding with constant speed ($zero$ acceleration).
Thus, we can tell that there are three forces acting on the brick, its weight which is directed downward, the normal force exerted by the tabletop which is directed upward, and the force exerted by the spring.
Since the brick stills at rest, there is no acceleration.
So, we apply $textbf{Newton’s first law}$ to the brick in the vertical direction, so we get:
$$
begin{align*}
sum F_y = F + N – mg &= 0\\
N &= mg – F
end{align*}
$$
As we can see, the normal force equals the weight of the brick minus the force exerted by the spring.
Therefore, the normal force acting on the brick is $textbf{less than}$ the brick’s weight.
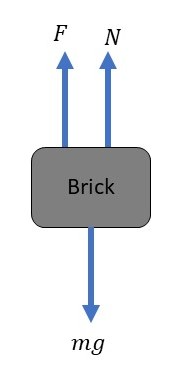
textbf{ Less than}
$$
Taking upward as the positive directed, we apply $textbf{Newton’s second law}$ to you in the vertical direction, so we get:
$$
begin{align*}
sum F_y = F_b – w &= ma\\
a &= dfrac{F_b – w}{m}
end{align*}
$$
In order to decelerate, you need to have an upward acceleration (positive acceleration).
And according to equation (1), to have a positive acceleration, the force exerted on you by the parachute must be $textbf{greater than}$ your weight.
(b) The best explanation is
$textbf{C.}$ To decelerate a skydiver in free fall, the net force acting on the skydiver must be upward.
(b) The right choice is $textbf{C}$
From $textbf{Newton’s second law}$ for multiple forces, the net force on an object is equal to its mass times its acceleration:
$$
begin{gather*}
sum vec{textbf{F}} = mvec{textbf{a}}tag{1}
end{gather*}
$$
Let the $+x$ direction is due right and the $+y$ direction is due upward.
For puck A, the net force exerted on the puck in the $x$ direction is:
$$
begin{align*}
sum F_x = (+7.0text{ N}) + (- 5.0text{ N}) = +2.0text{ N}
end{align*}
$$
And there are no vertical forces, so the magnitude of the net force on the puck is $sum F = 2.0text{ N}$.
From $textbf{Newton’s second law}$, the magnitude of the acceleration of puck A is:
$$
begin{gather*}
boxed{a_A = dfrac{2.0text{ N}}{m}}
end{gather*}
$$
For puck B, the net force exerted on the puck in the $x$ direction is:
$$
begin{align*}
sum F_x = +3.0text{ N}
end{align*}
$$
And the net force in the $y$ direction is:
$$
begin{gather*}
sum F_y = +3.0text{ N}
end{gather*}
$$
Thus, the magnitude of the net force on the puck is:
$$
begin{gather*}
sum F = sqrt{(3.0text{ N})^2 + (3.0text{ N})^2} = 4.24text{ N}
end{gather*}
$$
From $textbf{Newton’s second law}$, the magnitude of the acceleration of puck B is:
$$
begin{gather*}
boxed{a_B = dfrac{4.24text{ N}}{m}}
end{gather*}
$$
$$
begin{align*}
sum F_x = (+3.0text{ N}) + (3.0text{ N}) cos{theta} = +3.0 (1 + cos{theta})text{ N}
end{align*}
$$
And the net force in the $y$ direction is:
$$
begin{gather*}
sum F_y = (+3.0text{ N}) sin{theta}
end{gather*}
$$
Thus, the magnitude of the net force on the puck is:
$$
begin{align*}
sum F &= sqrt{(3.0text{ N})^2 + (3.0text{ N})^2 cos^2{theta} + 6.0cos{theta} + (3.0text{ N})^2 sin^2{theta}}\\
& = sqrt{(3.0text{ N})^2 + (3.0text{ N})^2 + 6.0 cos{theta}} > 4.24text{ N}
end{align*}
$$
From $textbf{Newton’s second law}$, the magnitude of the acceleration of puck C is:
$$
begin{gather*}
boxed{a_C > dfrac{4.24text{ N}}{m}}
end{gather*}
$$
For puck D, the net force exerted on the puck in the $x$ direction is:
$$
begin{align*}
sum F_x = +3.0text{ N}
end{align*}
$$
And there are no forces in the $y$ direction, so, the magnitude of the net force on the puck is $sum F = 3.0$ N.
From $textbf{Newton’s second law}$, the magnitude of the acceleration of puck D is:
$$
begin{gather*}
boxed{a_D = dfrac{3.0text{ N}}{m}}
end{gather*}
$$
Therefore, $a_A < a_D < a_B < a_C$ .
a_A < a_D < a_B < a_C
$$
From $textbf{Newton’s second law}$ for multiple forces, the net force on an object is equal to its mass times its acceleration:
$$
begin{gather*}
sum vec{textbf{F}} = m vec{textbf{a}}tag{1}
end{gather*}
$$
From $textbf{Newton’s second law}$, the weight of an objetc is equal to its mass times the acceleration due to gravity:
$$
begin{gather*}
w = mgtag{2}
end{gather*}
$$
The mass of the rock is $m = 5.00$ kg, its weight on that particular planet is $w = 40.0$ N and the magnitude of the force exerted by you on the rock is $F_a = 46.2$ N.
Let upward be the positive direction.
The applied force is directed upward and we know that weight is always directed downward.
So, we apply $textbf{Newton’s second law}$ to the rock in the $y$ direction, so we get:
$$
begin{align*}
sum vec{textbf{F}} = F_a – w &= ma\\
a & = dfrac{F_a – w}{m}
end{align*}
$$
Now, we plug our values for $m$, $w$ and $F_a$, so we get the acceleration of the rock:
$$
begin{gather*}
a = dfrac{46.2text{ N} – 40.0text{ N}}{5.00text{ kg}} = 1.24text{ m/s}^2\\
therefore quad large boxed{a = 1.24text{ m/s}^2text{ upward}}
end{gather*}
$$
And since the bag and the cart are stationary, there are no horizontal forces on the bag.
(b) When the cart is moving horizontally with constant speed, there are two forces acting on the cart, one is the pushing force and the other is the friction due to the ground.
Since there is no acceleration, both forces are equal in magnitude and opposite in direction so they cancel each other.
But for the bag, there are no horizontal forces acting on it.
Therefore, the free diagram of the bag does not change.
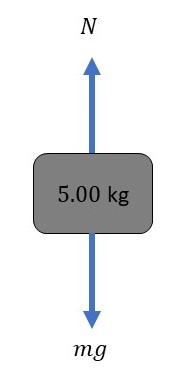
(b) The free diagram does not change, since there is still no horizontal acceleration for the bag.
From $textbf{Hooke’s law}$, the restoring force exerted by an ideal spring of constant $k$ is proportional to the distance of its stretch or compression $x$:
$$
begin{gather*}
F = kxtag{1}
end{gather*}
$$
The constant of the spring is $k = 55.0$ N/m and the distance of its stretch is $x= 0.120$ m.
We simply plug our values for $k$ and $x$ into equation (1), so we get the force required to stretch the spring this distance:
$$
begin{gather*}
F = (55.0text{ N/m}) cdot (0.120text{ m}) = 6.60text{ N}\\
therefore quad large boxed{F = 6.60text{ N}}
end{gather*}
$$
From $textbf{Hooke’s law}$, the restoring force exerted by an ideal spring of constant $k$ is proportional to the distance of its stretch or compression $x$:
$$
begin{gather*}
F = kxtag{1}
end{gather*}
$$
The constant of the spring is $k = 71.0$ N/m and the force required to compress it is $F= 4.30$ N.
We simply plug our values for $k$ and $F$ into equation (1) and evaluate for $x$, so we get the distance of compression:
$$
begin{gather*}
x = dfrac{F}{k} = dfrac{4.30text{ N}}{71.0text{ N/m}} = 0.0606text{ m}\\
therefore quad large boxed{x = 6.06text{ cm}}
end{gather*}
$$
From $textbf{Hooke’s law}$, the restoring force exerted by an ideal spring of constant $k$ is proportional to the distance of its stretch or compression $x$:
$$
begin{gather*}
F = kxtag{1}
end{gather*}
$$
The distance of stretch is $x = 0.095$ m and the force required for this distance is $F= 4.80$ N.
We simply plug our values for $x$ and $F$ into equation (1) and evaluate for $k$, so we get the spring constant:
$$
begin{gather*}
k = dfrac{F}{x} = dfrac{4.80text{ N}}{0.095text{ m}} = 50.5text{ N/m}\\
therefore quad large boxed{k = 50.5text{ N/m}}
end{gather*}
$$
k = 50.5text{ N/m}
$$
From $textbf{Hooke’s law}$, the restoring force exerted by an ideal spring of constant $k$ is proportional to the distance of its stretch or compression $x$:
$$
begin{gather*}
F = kxtag{1}
end{gather*}
$$
From $textbf{Newton’s second law}$, the weight of an object is equal to its mass times the acceleration due to gravity:
$$
begin{gather*}
w = mgtag{2}
end{gather*}
$$
The mass of the spider is $m = 26.0times 10^{-5}$ kg and the constant of the spring is $k = 7.10$ N/m.
While the spider is hanged from its thread, there are two forces acting on it, one is its weight directed downward and the other is the restoring force exerted by the thread (due to its stretch) upward.
Since the spider is stationary, we apply $textbf{Newton’s first law}$ in the $y$ direction, so we get:
$$
begin{gather*}
sum F_y = F_s – w = 0\\
F_s = w
end{gather*}
$$
Substituting equation (1) and (2), we get:
$$
begin{gather*}
kx = mg
end{gather*}
$$
Solving for $x$, we get:
$$
begin{gather*}
x = dfrac{mg}{k}
end{gather*}
$$
Finally, we plug our values for $m$, $g$ and $k$, so we get the distance of stretch of the thread:
$$
begin{gather*}
x = dfrac{(26.0times 10^{-5}text{ kg}) (9.81text{ m/s}^2)}{7.10text{ N/m}} = 3.59times 10^{-4}text{ m}\\
therefore quad large boxed{x = 0.359text{ mm}}
end{gather*}
$$
From $textbf{Hooke’s law}$, the restoring force exerted by an ideal spring of constant $k$ is proportional to the distance of its stretch or compression $x$:
$$
begin{gather*}
F = kxtag{1}
end{gather*}
$$
The distance of stretch of the wire is $x = 0.110$ cm and its tension is $T = 360$ N.
The tension in the wire is equal to the restoring force exerted by the wire when it is stretched.
So, we plug our values for $T$ and $x$ into equation (1) and evaluate for $k$, so we get the spring constant of the wire:
$$
begin{gather*}
k = dfrac{T}{x} = dfrac{360text{ N}}{0.110times 10^{-2}text{ m}} = 327270text{ N/m}\\
therefore quad large boxed{k = 327270text{ N/m}}
end{gather*}
$$
k = 327270text{ N/m}
$$
From $textbf{Newton’s second law}$ for single force, the force exerted on an object is equal to its mass times its acceleration:
$$
begin{gather*}
F = matag{1}
end{gather*}
$$
From the velocity-time kinematic equation, the relation between the final speed, initial speed, acceleration, and time is:
$$
begin{gather*}
v_f = v_i + a ttag{2}
end{gather*}
$$
The mass of the sled is $m = 4.60$ kg, the magnitude of the force exerted on the sled is $F_a = 6.20$ N, its angle is $theta = 35.0text{textdegree}$, the initial speed of the sled is $v_i = 0$ and the time interval of the motion is $Delta t = 1.15$ s.
Since the ice surface is smooth, we can ignore any friction.
And since the motion is in the horizontal direction, we only need the horizontal component of the applied force.
$$
begin{gather*}
F_x = F_acos{theta} = (6.20text{ N}) cos{35.0text{textdegree}} = 5.08text{ N}
end{gather*}
$$
In the horizontal direction, the $x$-compoent of the applied force is the only force acting on the sled, so we plug our values for $F_x$ and $m$ into equation (1) and evalute for $a$, so we get the acceleration of the sled:
$$
begin{gather*}
a = dfrac{F_x}{m} = dfrac{5.08text{ N}}{4.60text{ kg}} = 1.10text{ m/s}^2
end{gather*}
$$
Finally, we plug our values for $v_i$, $a$ and $Delta t$ into equation (2), so we get the final speed of the sled:
$$
begin{gather*}
v_f = 0 + (1.10text{ m/s}^2) (1.15text{ s}) = 1.27text{ m/s}\\
therefore quad large boxed{v_f = 1.27text{ m/s}}
end{gather*}
$$
From $textbf{Newton’s second law}$ for multible forces, the net force exerted on an object is equal to its mass times its acceleration:
$$
begin{gather*}
sum vec{textbf{F}} = mvec{textbf{a}}tag{1}
end{gather*}
$$
The mass of the child is $m_c = 19.0$ kg, the mass of the sled is $m_s = 3.70$ kg, the magnitude of the force exerted by each teenager is $F_a = 55.0$ N with an angle of $theta = 35.0text{textdegree}$ relative to the forward direction and the magnitude of the force exerted by the snow is $F_text{snow} = 57.0$ N.
First, we need to get the component of the force exerted by each teenager in the forward direction:
$$
begin{gather*}
F_{a,x} = F_x cos{theta} = (55.0text{ N}) cos{35.0text{textdegree}} = 45.1text{ N}
end{gather*}
$$
So, along the direction of motion, there are three forces acting on the sled, two are the components of the forces exerted by the teenagers which are directed forward and the other is the retarding force exerted by the snow which is directed backward.
Thus, we apply $textbf{Newton’s second law}$ to the sled in the $x$ direction, so we get:
$$
begin{gather*}
sum F_x = F_{a,x} + F_{a,x} – F_{text{snow}} = (m_s + m_c) a\\
a = dfrac{2F_{a,x} – F_text{snow}}{m_s + m_c}
end{gather*}
$$
Fianlly, we plug our values for $F_{a,x}$, $F_text{snow}$, $m_s$ and $m_c$, so we get the acceleration of the sled and child:
$$
begin{gather*}
a = dfrac{2 (45.1text{ N}) – 57.0text{ N}}{3.70text{ kg} + 19.0text{ kg}} = 1.46text{ m/s}^2\\
therefore quad large boxed{a = 1.46text{ m/s}^2}
end{gather*}
$$
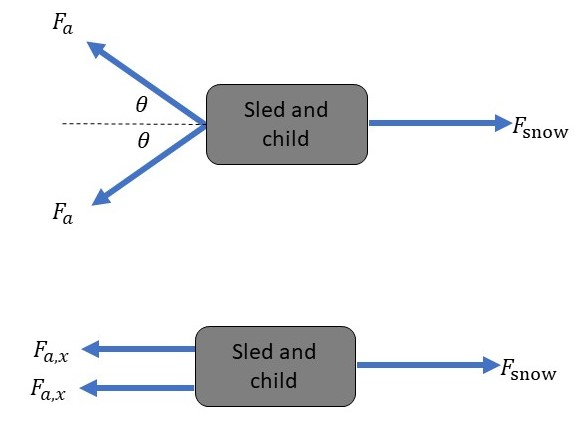
a = 1.46text{ m/s}^2
$$
From $textbf{Newton’s second law}$ for multiple forces, the net force on an object is equal to its mass times its acceleration:
$$
begin{gather*}
sum vec{textbf{F}} = m vec{textbf{a}}tag{1}
end{gather*}
$$
The force exerted by the first astronaut has a magnitude of $F_1 = 45.0$ N directed in the $+x$ direction and the force exerted by the second astronaut has a magnitude of $F_2 = 68.0$ N at an angle $theta = 55.0text{textdegree}$ above the $+x$-axis.
The magnitude of the acceleration of the satellite is $a = 0.120text{ m/s}^2$.
(a) First, we need to resolve the two forces into their components as follows:
$$
begin{align*}
F_{1,x} & = F_1 = 45.0text{ N}\\
F_{1,y} & = 0 \\
F_{2,x} & = F_2 cos{theta} \
& = (68.0text{ N}) cos{55.0text{textdegree}} = 39.0text{ N}\\
F_{2,y} & = F_2 sin{theta} \
& = (68.0text{ N}) sin{55.0text{textdegree}} = 55.7text{ N}
end{align*}
$$
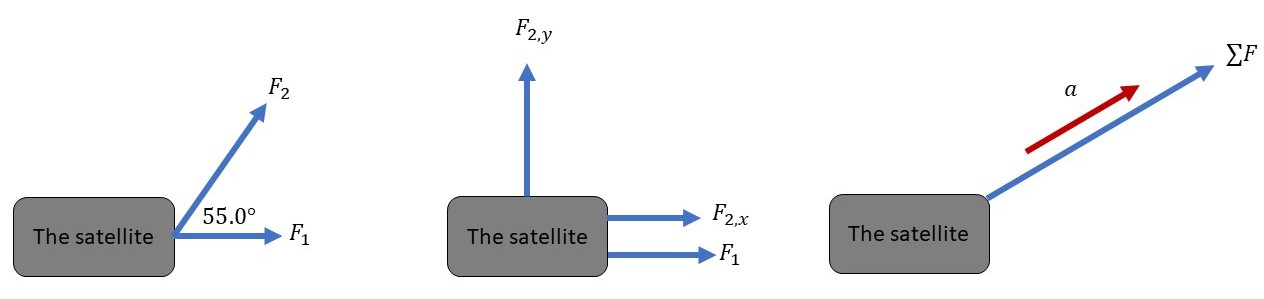
$$
begin{align*}
sum F_x & = F_{1,x} + F_{2,x} = 45.0text{ N} + 39.0text{ N} = 84.0text{ N}\\
sum F_y & = F_{1,y} + F_{2,y} = 0 + 55.7text{ N} = 55.7text{ N}
end{align*}
$$
Thus, the magnitude of the net force is:
$$
begin{gather*}
sum F = sqrt{(84.0text{ N})^2 + (55.7text{ N})^2} = 92.6text{ N}\\
therefore quad large boxed{sum F = 92.6text{ N}}
end{gather*}
$$
And its direction is:
$$
begin{gather*}
phi = tan^{-1}{dfrac{sum F_y}{sum F_x}} = tan^{-1}{dfrac{55.7}{84.0}} = 33.5text{textdegree}\\
therefore quad large boxed{phi = 33.5text{textdegree}text{ above the $+x$-axis}}
end{gather*}
$$
For the mass of the satellite, we plug our values for $sum F$ and $a$ into equation (1) and evaluate for $m$, so we get:
$$
begin{gather*}
m = dfrac{sum F}{a} = dfrac{92.6text{ N}}{0.120text{ m/s}^2} = 772text{ kg}\\
therefore quad large boxed{m = 772text{ kg}}
end{gather*}
$$
(b) $m = 772$ kg
From $textbf{Newton’s second law}$ for multiple forces, the net force on an object is equal to its mass times its acceleration:
$$
begin{gather*}
sum vec{textbf{F}} = m vec{textbf{a}}tag{1}
end{gather*}
$$
The mass of the satellite is $m = 680$ kg.
The magnitude of the force exerted by astronaut 1 is $F_1 = 52.0$ N in the $+x$ direction.
The magnitude of the force exerted by astronaut 2 is $F_2 = 35.0$ N in the $-y$ direction.
The magnitude of the force exerted by astronaut 3 is $F_3 = 74.0$ N at an angle of $theta = 63text{textdegree}$ above $+x$-axis.
(a) First, we resolve the forces into their components in the $x$ and $y$ directions as follows:
$$
begin{align*}
F_{1,x} &= F_1 = 52.0text{ N}\\
F_{1,y} &= 0\\
F_{2,x} &= 0 \\
F_{2,y} &= -F_2 = -35.0text{ N}\\
F_{3,x} &= F_3 cos{theta} \
& = (74.0text{ N}) cos{63} = 33.6text{ N}\\
F_{3,y} &= F_3 sin{theta} \
& = (74.0text{ N}) sin{63} = 65.9text{ N}
end{align*}
$$
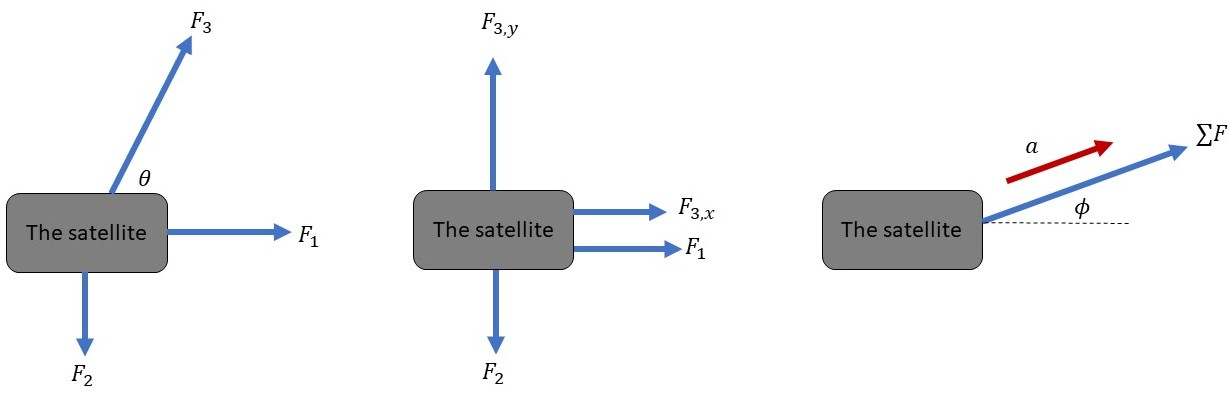
So, we get:
$$
begin{align*}
sum F_x &= F_{1,x} + F_{2,x} + F_{3,x}\
& = 52.0text{ N} + 0 + 33.6text{ N} = 85.6text{ N}\\
sum F_y &= F_{1,y} + F_{2,y} + F_{3,y}\
& = 0 – 35.0text{ N} + 65.9text{ N} = 30.9text{ N}
end{align*}
$$
Thus, the magnitude of the net force is:
$$
begin{align*}
sum F &= sqrt{ left( sum F_x right)^2 + left(sum F_yright)^2}\\
& = sqrt{(85.6text{ N})^2 + (30.9text{ N})^2} = 91.0text{ N}
end{align*}
$$
$$
therefore quad large boxed{sum F = 91.0text{ N}}
$$
And its direction is:
$$
begin{gather*}
phi = tan^{-1}{dfrac{sum F_y}{sum F_x}} = tan^{-1}{dfrac{30.9}{85.6}} = 19.8text{textdegree}\\
therefore quad large boxed{phi = 19.8text{textdegree}text{ above the $+x$-axis}}
end{gather*}
$$
For the magnitude of the acceleration of the satellite, we plug our values for $sum F$ and $m$ into equation (1) and evaluate for $a$, so we get:
$$
begin{gather*}
a = dfrac{sum F}{m} = dfrac{91.0text{ N}}{680text{ kg}} = 0.134text{ m/s}^2\\
therefore quad large boxed{a = 0.134text{ m/s}^2}
end{gather*}
$$
(b) $a = 0.134text{ m/s}^2$ in the same direction as the net force.
First, we resolve the applied force into its components as follows:
$$
begin{align*}
F_x & = F cos{theta}\\
F_y & = F sin{theta}
end{align*}
$$
We take upward as the positive direction, so we have three forces acting on the suitcase in the vertical direction, the normal force and the $y$-component of the applied force are upward and the weight of the suitcase is downward.
Since the suitcase has no acceleration in the vertical direction, we apply $textbf{Newton’s first law}$ in the $y$ direction, so we get:
$$
begin{align*}
sum F = N + F sin{theta} – mg &= 0\\
F sin{theta} & = mg – N\\
F & = dfrac{mg – N}{sin{theta}}tag{1}
end{align*}
$$
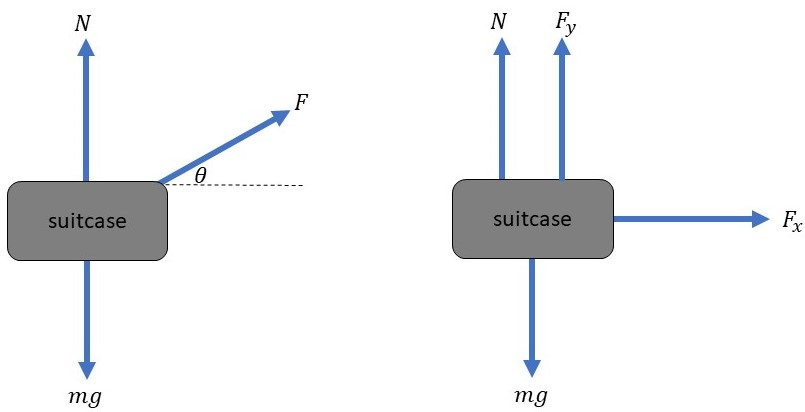
We can see for all the curves that the normal force equals the weight at $theta = 0$ where $sin{theta} = 0$ and there is no a $y$-component for the applied force.
So we can get the applied force for each curve by substituting for the value of the normal force and the corresponding angle into equation (1).
For curve (a), we substitute for $theta = 90text{textdegree}$ and $N = mg/2$ into equation (1), so we get:
$$
begin{gather*}
F_{(a)} = dfrac{mg – frac{mg}{2}}{sin{90}} = dfrac{mg}{2}\\
therefore quad large boxed{F_{(a)} = dfrac{mg}{2}}
end{gather*}
$$
For curve (b), we substitute for $theta = 90text{textdegree}$ and $N = 0$ into equation (1), so we get:
$$
begin{gather*}
F_{(b)} = dfrac{mg – 0}{sin{90}} = mg\\
therefore quad large boxed{F_{(b)} = mg}
end{gather*}
$$
For curve (c), we substitute for $theta = 30text{textdegree}$ and $N = 0$ into equation (1), so we get:
$$
begin{gather*}
F_{(c)} = dfrac{mg – 0}{sin{30}} = dfrac{mg}{0.5}\\
therefore quad large boxed{F_{(c)} = 2mg}
end{gather*}
$$
$F_{(b)} = mg$
$F_{(c)} = 2mg$
Notice that since the bricks are not changed, the net weight would be the same for both cases, and so are the net normal forces. The net frictional force is the product of the coefficient of kinetic friction and the net normal force, and these quantities are equal for both cases. Hence, the kinetic friction in case 1 is $textbf{equal}$ to the kinetic friction in case 2.
From the explanation above, the correct choice would be $textbf{B.}$ “the normal force i the same in the two cases, and friction is independent of surface area.”
The rear wheels of driver 1 would experience kinetic friction since the wheels are locked, while the rear wheels of driver 2 would remain in static friction. Driver 1 would experience less friction force, and would therefore have $textbf{greater}$ stopping distance than driver 2.
From the explanation above, the best choice is $textbf{C.}$ “locked brakes result in sliding (kinetic) friction, which is less than rolling (static) friction.”
The $textbf{kinetic friction}$ on an object is directly proportional to the normal force on it,
$$
begin{gather*}
f_k = mu_k Ntag{1}
end{gather*}
$$
Where $mu_k$ is the coefficient of kinetic friction.
The mass of the player is $m =55.0$ kg, his initial speed is $v_i = 4.60$ m/s and the coefficient of kinetic friction between the player and the ground is $mu_k = 0.460$ .
While the player is sliding, there is no acceleration in the vertical direction and there are two forces acting on him, his weight directed downward and the normal force directed upward.
So, we apply $textbf{Newton’s first law}$ in the $y$ direction, so we get:
$$
begin{align*}
sum F_y = N – w &= 0\\
N &= w = mg
end{align*}
$$
Now, we plug our values for $m$ and $g$, so we get the normal force on the player:
$$
begin{gather*}
N = (55.0text{ kg}) cdot (9.81text{ m/s}^2) = 540text{ N}
end{gather*}
$$
For the horizontal direction, there is only the kinetic friction force acting on the player (opposite to his motion).
So, we apply $textbf{Newton’s second law}$ to the player in the $x$ direction, so we get:
$$
begin{align*}
sum F_x = -f_k &= ma\\
-mu_k N & = ma \\
a &= – dfrac{mu_k N}{m}
end{align*}
$$
Finally, we plug our values for $mu_k$, $N$ and $m$, so we get the acceleration of the player:
$$
begin{gather*}
a = – dfrac{(0.460) (540text{ N})}{55.0text{ kg}} = -4.51text{ m/s}^2\\
therefore quad large boxed{a = -4.51text{ m/s}^2}
end{gather*}
$$
a = -4.51text{ m/s}^2
$$
The $textbf{kinetic friction}$ on an object is directly proportional to the normal force on it,
$$
begin{gather*}
f_k = mu_k Ntag{1}
end{gather*}
$$
Where $mu_k$ is the coefficient of kinetic friction.
While the player is sliding, there is no acceleration in the vertical direction and there are two forces acting on him, his weight directed downward and the normal force directed upward.
So, we apply $textbf{Newton’s first law}$ in the $y$ direction, so we get:
$$
begin{align*}
sum F_y = N – w &= 0\\
N &= w = mg tag{2}
end{align*}
$$
For the horizontal direction, there is only the kinetic friction force acting on the player (opposite to his motion).
So, we apply $textbf{Newton’s second law}$ to the player in the $x$ direction, so we get:
$$
begin{align*}
sum F_x = -f_k &= ma\\
-mu_k N & = ma
end{align*}
$$
Substituting for $N$ form equation (2), we get:
$$
begin{align*}
-mu_k m g &= ma\\
a & = -mu_k gtag{3}
end{align*}
$$
So, the acceleration of the player does not depend on the mass.
Therefore, If the mass of the baseball player in Problem 96 is doubled, his acceleration $textbf{stays the same}$.
(b) So form equation (3), the acceleration of the player, whatever his mass, is:
$$
begin{gather*}
a = – (0.460) (9.81text{ m/s}^2) = -4.51text{ m/s}^2\\
therefore quad large boxed{a = -4.51text{ m/s}^2}
end{gather*}
$$
(b) $a = -4.51text{ m/s}^2$
The $textbf{kinetic friction}$ on an object is directly proportional to the normal force on it,
$$
begin{gather*}
f_k = mu_k Ntag{1}
end{gather*}
$$
Where $mu_k$ is the coefficient of kinetic friction.
While the player is sliding, there is no acceleration in the vertical direction and there are two forces acting on him, his weight directed downward and the normal force directed upward.
So, we apply $textbf{Newton’s first law}$ in the $y$ direction, so we get:
$$
begin{align*}
sum F_y = N – w &= 0\\
N &= w = mg tag{2}
end{align*}
$$
For the horizontal direction, there is only the kinetic friction force acting on the player (opposite to his motion).
So, we apply $textbf{Newton’s second law}$ to the player in the $x$ direction, so we get:
$$
begin{align*}
sum F_x = -f_k &= ma\\
-mu_k N & = ma
end{align*}
$$
Substituting for $N$ form equation (2), we get:
$$
begin{align*}
-mu_k m g &= ma\\
a & = -mu_k gtag{3}
end{align*}
$$
So, the acceleration of the player depends only on the coefficient of kinetic friction and the initial speed does not have anything to do with the acceleration.
Therefore, If the speed of the baseball player in Problem 96 is halved, his acceleration $textbf{stays the same}$.
(b) So form equation (3), the acceleration of the player, whatever his mass, is:
$$
begin{gather*}
a = – (0.460) (9.81text{ m/s}^2) = -4.51text{ m/s}^2\\
therefore quad large boxed{a = -4.51text{ m/s}^2}
end{gather*}
$$
(b) $a = -4.51text{ m/s}^2$
The $textbf{maximum static friction}$ is directly proportional to the normal force:
$$
begin{gather*}
f_{s,max} = mu_s Ntag{1}
end{gather*}
$$
Where $mu_s$ is the coefficient of static friction.
The acceleration of the car is $a = 12.0text{ m/s}^2$.
There is no acceleration in the vertical direction, and there are two forces acting on the car in the vertical direction, one is its weight directed downward and the other is the normal force directed upward.
By applying $textbf{Newton’s first law}$ in the vertical direction, we get:
$$
begin{align*}
sum F_y = N – w &= 0\\
N &= w = mgtag{2}
end{align*}
$$
In the horizontal direction, the static friction force is the only force acting on the car.
For the minimum $mu_s$, we take the static friction to be maximum.
And by applying $textbf{Newton’s second law}$ in the horizontal direction, we get:
$$
begin{align*}
sum F_x = f_{s,max} &= ma
end{align*}
$$
Now, we substitute for $f_{s,max}$ from equation (1), so we get:
$$
begin{gather*}
mu_s N = ma
end{gather*}
$$
Then, we substitute for $N$ from equation (2), so we get:
$$
begin{align*}
mu_s m g &= ma\\
mu_s g &= a\\
mu_s&= dfrac{a}{g}
end{align*}
$$
Finally, we plug our values for $a$ and $g$, so we get the minimum coefficicent of static friction:
$$
begin{gather*}
mu_s = dfrac{12.0text{ m/s}^2}{9.81text{ m/s}^2} = 1.22\\
therefore quad large boxed{mu_s = 1.22}
end{gather*}
$$
mu_s = 1.22
$$
The $textbf{maximum static friction}$ is directly proportional to the normal force:
$$
begin{gather*}
f_{s,max} = mu_s Ntag{1}
end{gather*}
$$
Where $mu_s$ is the coefficient of static friction.
From $textbf{velocity-position}$ kinematic equation, the relation between the initial speed, final speed, acceleration and the change in position is:
$$
begin{gather*}
v_f^2 = v_i^2 + 2aDelta xtag{2}
end{gather*}
$$
The sprinter’s initial speed is $v_i = 0$ and final speed is $v_f = 13.0$ m/s, reaching this final speed after a distance $Delta x = 22.0$ m.
First, we plug our values for $v_i$, $v_f$ and $Delta x$ into equation (2) and solve for $a$, so we get the required acceleration the sprinter should have:
$$
begin{gather*}
a= dfrac{v_f^2 – v_i^2}{2Delta x} = dfrac{(13.0text{ m/s})^2 – (0)^2}{2 (22.0text{ m})} = 3.84text{ m/s}^2
end{gather*}
$$
There is no acceleration in the vertical direction, and there are two forces acting on the sprinter in the vertical direction, one is his weight directed downward and the other is the normal force directed upward.
By applying $textbf{Newton’s first law}$ in the vertical direction, we get:
$$
begin{align*}
sum F_y = N – w &= 0\\
N &= w = mgtag{3}
end{align*}
$$
To get the minimum coefficient f static friction, we take the static friction to be maximum.
So, by applying $textbf{Newton’s second law}$ in the horizontal direction, we get:
$$
begin{align*}
sum F_x = f_{s,max} &= ma
end{align*}
$$
Now, we substitute for $f_{s,max}$ from equation (1), so we get:
$$
begin{gather*}
mu_s N = ma
end{gather*}
$$
Then, we substitute for $N$ from equation (3), so we get:
$$
begin{align*}
mu_s m g &= ma\\
mu_s g &= a\\
mu_s&= dfrac{a}{g}
end{align*}
$$
Finally, we plug our values for $a$ and $g$, so we get the minimum coefficient of static friction required for the sprinter to reach his goal:
$$
begin{gather*}
mu_s = dfrac{3.84text{ m/s}^2}{9.81text{ m/s}^2} = 0.392\\
therefore quad large boxed{mu_s = 0.392}
end{gather*}
$$
mu_s = 0.392
$$
$$
begin{align*}
F_c &le f_{s,max}\
ma&le mu_s N\
ma&le mu_smg\
a&le mu_sg=boxed{color{#4257b2}{2.35frac{m}{s^2}}}
end{align*}
$$
$$
begin{align*}
a&le a_{max}\
frac{Delta v}{Delta t}&le a_{max}\
frac{Delta v}{a_{max}}&le Delta t \
frac{(15m/s)}{(2.35m/s^2)}&le Delta t \
boxed{color{#4257b2}{6.38s}}&leDelta t
end{align*}
$$
b) $Delta t ge 0.38 ~s$
The $textbf{maximum static friction}$ is directly proportional to the normal force:
$$
begin{gather*}
f_{s,max} = mu_s Ntag{1}
end{gather*}
$$
Where $mu_s$ is the coefficient of static friction.
The coefficient of static friction is $mu_s = 0.250$ .
First, we resolve the weight into two components, one component is parallel to the incline and the other is perpendicular to the incline.
Thus, we have:
$$
begin{align*}
w_{bot} &= -mg cos{theta}\\
w_{parallel} & = mg sin{theta}
end{align*}
$$
We know that the normal force always acts normal to the surface.
Since the block has no acceleration in the perpendicular direction, we apply $textbf{Newton’s first law}$ in this direction, so we get:
$$
begin{align*}
sum F_{bot} &= N – mg cos{theta} = 0\\
N & = mg cos{theta}
end{align*}
$$
Substituting into equaton (1), we get the maximum static friction on the block:
$$
begin{gather*}
f_{s,max} = mu_s m g cos{theta}tag{2}
end{gather*}
$$
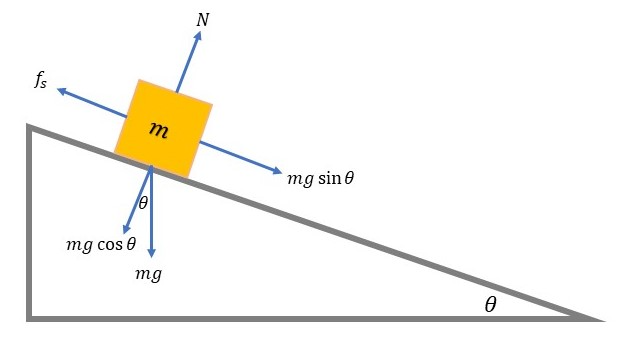
As the angle of the incline increases, the component of the weight increases and so the static friction.
Just when the block starts to move (and before it actually moves), the static friction is maximum and at this moment it equals the parallel component of weight.
By applying $textbf{Newton’s first law}$ at this moment in the parallel direction, we get:
$$
begin{align*}
sum F_{parallel} & = mg sin{theta} – f_{s,max} = 0\\
mg sin{theta} & = f_{s,max}
end{align*}
$$
Substituting for $f_{s,max}$ from equation (2), so we get:
$$
begin{align*}
mg sin{theta} & = mu_s m g cos{theta}\\
sin{theta} & = mu_s cos{theta}\\
dfrac{sin{theta}}{cos{theta}} & = tan{theta} = mu_s\\
theta & = tan^{-1}{mu_s}
end{align*}
$$
Finally, we plug our value for $mu_s$, so we get the angle of the incline at which the block starts to move:
$$
begin{gather*}
theta = tan^{-1}{0.250} = 14.0text{textdegree}\\
therefore quad large boxed{theta = 14.0text{textdegree}}
end{gather*}
$$
theta = 14.0text{textdegree}
$$
The **maximum static friction** is directly proportional to the normal force:
$$begin{gather*}
f_{s,max} = mu_s Ntag{1}
end{gather*}$$
Where $mu_s$ is the coefficient of static friction.
The **kinetic friction** is directly proportional to the normal force:
$$begin{gather*}
f_{k} = mu_k Ntag{2}
end{gather*}$$
Where $mu_s$ is the coefficient of kinetic friction.
The mass of the book is $m = 1.92 mathrm{kg}$, the force required to make the book moves is $F_{a,s} = 2.05 mathrm{ N}$ and the force required to keep the book moving with constant speed is $F_{a,k} = 1.03 mathrm{N}$.
Whether the book is at rest or moving, there is no acceleration in the vertical direction.
And there are two forces acting on the book in the vertical direction, one is its weight directed downward and the other is the normal force directed upward.
So, we apply **Newton’s first law** to the book in the vertical direction, so we get:
$$begin{align*}
sum F_y & = N – mg = 0\
N & = mg
end{align*}$$
We plug our values for $m$ and $g$, so we get the normal force on the book:
$$begin{gather*}
N = (1.92text{ kg}) cdot (9.81text{ m/s}^2) = 18.8text{ N}
end{gather*}$$
As we increase the applied force it keeps increasing and until it reaches its maximum value.
When the applied force equals the maximum friction force, the book starts to move.
So, in the horizontal direction, there are two forces acting on the book, one is the applied force (positive direction), and the static friction force (negative direction).
So, we apply **Newton’s first law** at the moment when the book starts to move (but does not actually move) in the horizontal direction, so we get:
$$begin{align*}
sum F_x = F_{a,s} – f_{s,max} &= 0\
f_{s,max} & = F_{a,s} = 2.05text{ N}
end{align*}$$
Now, we plug our values for $N$ and $f_{s,max}$ into equation (1) and evaluate for $mu_s$, so we get the coefficient of static friction:
$$begin{gather*}
mu_s = dfrac{f_{s,max}}{N} = dfrac{2.05text{ N}}{18.8text{ N}} = 0.109\
therefore quad large boxed{mu_s = 0.109}
end{gather*}$$
So, we apply **Newton’s first law** in the horizontal direction, so we get:
$$begin{align*}
sum F_x &= F_{a,k} – f_k = 0\\
f_k & = F_{a,k} = 1.03text{ N}
end{align*}$$
Finally, we plug our values for $N$ and $f_k$ into equation (2) and evaluate for $mu_k$, so we get the coefficient of kinetic friction:
$$begin{gather*}
mu_k = dfrac{f_k}{N} = dfrac{1.03text{ N}}{18.8text{ N}} = 0.055\
therefore quad large boxed{mu_k = 0.055}
end{gather*}$$
$$mu_k = 0.055$$
The only force acting on the cart is the force exerted by the horse, there are no other forces, thus, the net force on the cart is not $zero$; So, the cart moves.
But since the force exerted by gravity on a whole brick is greater than the force exerted by gravity on half a brick in a way that it is proportional to the mass;
Thus, the acceleration due to gravity is always constant (for a certain planet’s surface).
In this law, $ma$ is not the force itself, it is just a quantity that equals the force.
For an object in a free-fall, the force exerted on it is gravity.
And the gravitational for is directly proportional to the mass of the object, $F_g propto m$, thus,
$$
begin{gather*}
F_g = C m
end{gather*}
$$
Where $C$ is the proportionality constant.
In this equation, $Cm$ is the force itself.
Combining the two equations, we get:
$$
begin{gather*}
C m = ma\\
a = C
end{gather*}
$$
Therefore, the acceleration due to gravity is constant, which means that it does not depend on the mass of the falling object.
This means that the whole brick does need greater force to accelerate.
$$
begin{align*}
m &= frac{w_{1}}{g}
end{align*}
$$
$$
begin{align*}
ma &= N – mg \
ma &= w_{2} – w_{1} \
a &= frac{w_{2} – w_{1}}{m} \
&= frac{w_{2} – w_{1}}{w_{1}/g} \
&= g left( frac{w_{2} – w_{1}}{w_{1}} right) \
&= left( 9.81~mathrm{m/s^{2}} right) left( frac{480~mathrm{N} – 540~mathrm{N}}{540~mathrm{N}} right) \
&= -1.09~mathrm{m/s^{2}} \
a &= -1.1~mathrm{m/s^{2}}
end{align*}
$$
$$
boxed{1.1~mathrm{m/s^{2},~downwards} }
$$
For this part, the object is a car accelerating upward from a stoplight. The direction of acceleration is northward, so the net force is pointing $textbf{northward}$.
For this part, the object is a car traveling south and slowing down. Since the object is slowing down, its acceleration must be opposite of its velocity. The velocity is southward, so the acceleration, and the net force, are $textbf{northward}$.
For this part, the object is a car traveling westward with constant speed. The direction and magnitude of the velocity are constant, so the acceleration must be zero. The net force on the object is $textbf{zero}$.
For this part, the object is a skydiver parachuting downward with constant speed. The direction and magnitude of the velocity are constant, so the acceleration must be zero. The net force on the object is $textbf{zero}$.
For this part, the object is a baseball during it flight from pitcher to catcher (with zero air resistance). The object is in free-fall, so its acceleration and net force are pointing $textbf{toward the ground}$.
From $textbf{Hooke’s law}$, the restoration force exerted by an ideal spring with constant $k$ when it is compressed or stretched by a distance $x$ is given by:
$$
begin{gather*}
F = kxtag{1}
end{gather*}
$$
The spring constant is $k = 580$ N/m and the force exerted on the spring is $F = 51.0$ N.
We simply plug our values for $k$ and $F$ into equation (1) and evaluate for $x$, so we get the distance of compression of the spring:
$$
begin{gather*}
x = dfrac{F}{k} = dfrac{51.0text{ N}}{580text{ N/m}} = 0.0879text{ m}\\
therefore quad large boxed{x = 8.79text{ cm}}
end{gather*}
$$
x = 8.79text{ cm}
$$
From $textbf{Hooke’s law}$, the restoration force exerted by an ideal spring with constant $k$ when it is compressed or stretched by a distance $x$ is given by:
$$
begin{gather*}
F = kxtag{1}
end{gather*}
$$
The mass of the chimpanzee is $m = 22.0$ kg and the distance that the branch sags through is $x = 0.130$ m.
There are two vertical forces acting on the chimpanzee, one is its weight directed downward and the other is the restoring force exerted by the branch upward.
Since the chimpanzee is at rest, there is no acceleration; So, we apply $textbf{Newton’s first law}$ to the chimpanzee in the vertical direction, so we get:
$$
begin{align*}
sum F_y &= kx – mg = 0\\
kx & = mg\\
k & = dfrac{mg}{x}
end{align*}
$$
Finally, we plug our values for $m$, $g$ and $x$, so we get the spring constant of the branch:
$$
begin{gather*}
k = dfrac{(22.0text{ kg}) (9.81text{ m/s}^2)}{0.130text{ m}} = 1660text{ N/m}\\
therefore quad large boxed{k = 1660text{ N/m}}
end{gather*}
$$
k = 1660text{ N/m}
$$
For this part, the parachutist come to rest with constant acceleration over a distance $Delta x = 0.750~mathrm{m}$. We find the force exerted by the ground.
$$
begin{align*}
v_text{f}^{2} &= v_text{i}^{2} + 2a Delta x \
implies a &= frac{v_text{f}^{2} – v_text{i}^{2}}{2Delta x} tag{1}\
&= frac{0 – left( 3.85~mathrm{m/s} right)^{2}}{2 left( 0.750~mathrm{m} right)} \
a &= -9.88167~mathrm{m/s^{2}} \
end{align*}
$$
$$
begin{align*}
F &= ma \
&= left( 42.0~mathrm{kg} right) left( 9.88167~mathrm{m/s^{2}} right) \
&= 415.03000~mathrm{N} \
F &= boxed{ 415~mathrm{N} }
end{align*}
$$
We find the relationship between the force and the stopping distance. The magnitude of acceleration, from equation (1), is inversely proportional to $Delta x$.
$$
begin{align*}
a &propto frac{1}{Delta x} tag{2}
end{align*}
$$
$$
begin{align*}
F &propto a tag{3}
end{align*}
$$
$$
begin{align*}
F &propto frac{1}{Delta x}
end{align*}
$$
Since $Delta x$ is decreased, then $F$ must increase since the relationship is inverse proportional. Hence, for this case, the force exerted by the ground is $textbf{greater than}$ in part (a).
The velocity is constant, so the net force is 0. We have
$$
begin{align*}
vec{textbf{F}}_text{net} &= vec{textbf{F}}_text{air} – mg \
0 &= vec{textbf{F}}_text{air} – mg \
implies vec{textbf{F}}_text{air} &= mg tag{1} \
&= left( 1.21 times 10^{-3}~mathrm{kg} right) left( 9.81~mathrm{m/s^{2}} right) \
&= 1.18701 times 10^{-2}~mathrm{N} \
vec{textbf{F}}_text{air} &= boxed{ 1.2 times 10^{-2}~mathrm{N} }
end{align*}
$$
From equation (1), the force of air resistance is not dependent on the speed of the samara. In this case, the force of air resistance is $textbf{the same as}$ in part (a).
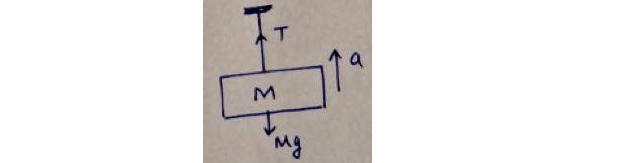
$a)quad FBD:$
Force balance in vertical direction :$quad T-Mg=Ma$
$Rightarrowquad underline{T=M(g+a)}$
$a> 0$ , so tension in the cable $(T)$ is $boxed{text{ greater than }}$ the combined weight $(Mg)$ of the two men.
from part$quad(a),quad T=M(g+a)$
.$qquadqquadquadRightarrow quad T=[(172)(9.81+1.10)]N$
.$qquadqquadquadRightarrow quad underline{Tapprox=(1876.5)N}$
So, tension in the cable $(T)=boxed{(1876.5)N}$
In this part, we find the number $n$ of geckos of mass $m_{1} = 0.25~mathrm{kg}$ that can be suspended by a single foot. The total weight of the geckos must be equal to $F_{1} = 11~mathrm{N}$.
$$
begin{align*}
F_{1} &= nm_{1}g \
implies n &= frac{F_{1}}{m_{1}g} \
&= frac{11~mathrm{N}}{left( 0.25~mathrm{kg} right) left( 9.81~mathrm{m/s^{2}} right)} \
&= 4.48522 \
n &= boxed{ 4.5~mathrm{geckos} }
end{align*}
$$
An average person has mass $m_{2} = 65~mathrm{kg}$. There are two shoe, with a total area of approximately $A_{2} = 250~mathrm{cm^{2}}$. The force exerted is the weight of the person. The force per unit square centimeter of a human is
$$
begin{align*}
frac{w_{2}}{A_{2}} &= frac{m_{2}g}{A_{2}} \
&= frac{left( 65~mathrm{kg} right) left( 9.81~mathrm{m/s^{2}} right)}{250~mathrm{cm^{2}}} \
&= 2.5506~mathrm{N/cm^{2}} \
frac{w_{2}}{A_{2}} &= 2.6~mathrm{N/cm^{2}}
end{align*}
$$
$$
begin{align*}
vec{textbf{F}} = 0 &= F sin theta_{2} – F_{1} sin theta_{1} \
implies F &= F_{1} frac{sin theta_{1}}{sin theta_{2}} \
&= left( 130~mathrm{N} right) frac{sin 34^{circ}}{sin 45^{circ}} \
&= 102.80636~mathrm{N} \
F &= boxed{ 1.0 times 10^{2}~mathrm{N} }
end{align*}
$$
F = 1.0 times 10^{2}~mathrm{N}
$$
$$
begin{align*}
vec{textbf{F}}_text{net} = 0 &= Mg – vec{textbf{F}}_text{air} \
implies vec{textbf{F}}_text{air} &= Mg
end{align*}
$$
$$
begin{align*}
vec{textbf{F}}_text{net} = left( M + m right)a &= left( M + m right)g – vec{textbf{F}}_text{air} \
left( M + m right)a &= left( M + m right)g – Mg\
Ma + ma &= mg \
implies m left(g – aright) &= Ma \
m &= frac{Ma}{g – a} \
&= frac{left( 1220~mathrm{kg} right) left( 0.56~mathrm{m/s^{2}} right)}{9.81~mathrm{m/s^{2}} – 0.56~mathrm{m/s^{2}}} \
&= 73.85946~mathrm{kg} \
m &= boxed{ 74~mathrm{kg} }
end{align*}
$$
m = 74~mathrm{kg}
$$
let the frictional force be $f$. For the two instances, the force equations are
$$
begin{align*}
ma_{1} &= F_{1} – f tag{1}\
ma_{2} &= F_{2} – ftag{2}
end{align*}
$$
$$
begin{align*}
m left( a_{2} – a_{1} right) &= F_{2} – F_{1} \
implies m &= frac{F_{2} – F_{1}}{a_{2} – a_{1}} \
&= frac{81~mathrm{N} – 75~mathrm{N}}{0.75~mathrm{m/s^{2}} – 0.50~mathrm{m/s^{2}}} \
m &= boxed{ 24~mathrm{kg} }
end{align*}
$$
The frictional force is equal to $f = mu_{k} N = mu_{k} mg$. Using equation (1), we have
$$
begin{align*}
ma_{1} &= F_{1} – f \
f &= F_{1} – ma_{1} \
mu_{k} mg &= F_{1} – ma_{1} \
implies mu_{k} &= frac{F_{1} – ma_{1}}{mg} \
&= frac{75~mathrm{N} – left( 24~mathrm{kg} right)left( 0.50~mathrm{m/s^{2}} right)}{left( 24~mathrm{kg} right)left( 9.81~mathrm{m/s^{2}} right)} \
&= 0.26758 \
mu_{k} &= boxed{ 0.27 }
end{align*}
$$
item [(a)] $m = 24~mathrm{kg}$
item [(b)] $mu_{k} = 0.27$
end{enumerate}
begin{center}
begin{tabular}{|c|c|c|}
hline
Substances & $mu_{s}$ & $mu_{k}$ \ hline
Rubber on wet concrete & $0.5-0.7$ & $0.3-0.5$ \ hline
Wood on wood & $0.5$ & $0.3$ \ hline
Steel on steel & $0.6$ & $0.3$ \ hline
Shoes on wood & $0.9$ & $0.7$ \ hline
end{tabular}
end{center}
$$
boxed{ mathrm{C.~} 1.05 times 10^{4}~mathrm{N} }
$$
mathrm{C.~} 105 times 10^{4}~mathrm{N}
$$
$$
boxed{ mathrm{C.~} 2.11 times 10^{5}~mathrm{N} }
$$
mathrm{C.~} 2.11 times 10^{5}~mathrm{N}
$$
$$
boxed{ mathrm{D.~} 4.21 times 10^{4}~mathrm{N} }
$$
mathrm{D.~} 4.21 times 10^{4}~mathrm{N}
$$

