Home Page Textbooks Physics Page 482: Lesson Check

Physics

1st Edition

Walker

ISBN: 9780133256925

Textbook solutions

All Solutions

Page 482: Lesson Check

Exercise 49

Step 1

1 of 7

Let us suppose we have two identical waves traveling in opposite direction with 1.0 m/s speed. Both of the waves have same positive head and the width of the pulse is also the same.

Therefore, the speeds of the first wave and the second wave are given as

$$
begin{align*}
v_1 & = 1.0 mathrm{m/s} \
v_2 & = -1.0 mathrm{m/s}
end{align*}
$$

As time passes the first wave move towards right and the second wave move towards left.

Step 2

2 of 7

$$
textbf{(a)}
$$

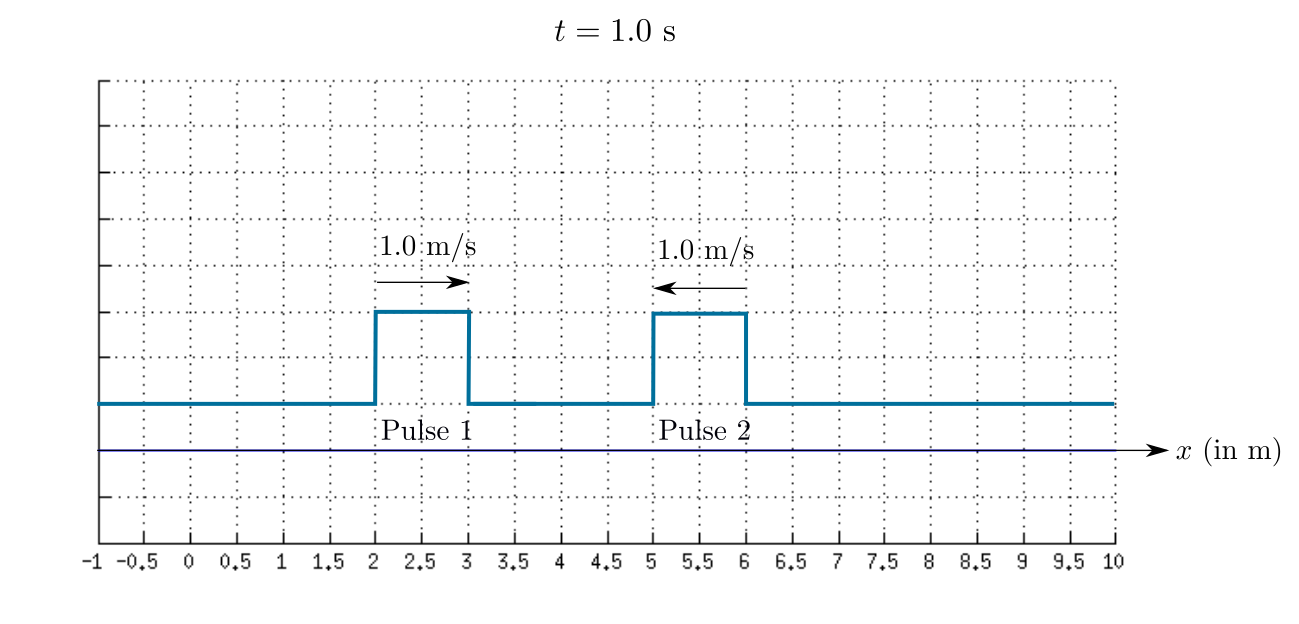
The sketch of the resultant waves at $t=1.0$ s is shown in the given figure.

In this graph, both the pulses are far from each other.

Exercise scan

Step 3

3 of 7

$$
textbf{(b)}
$$

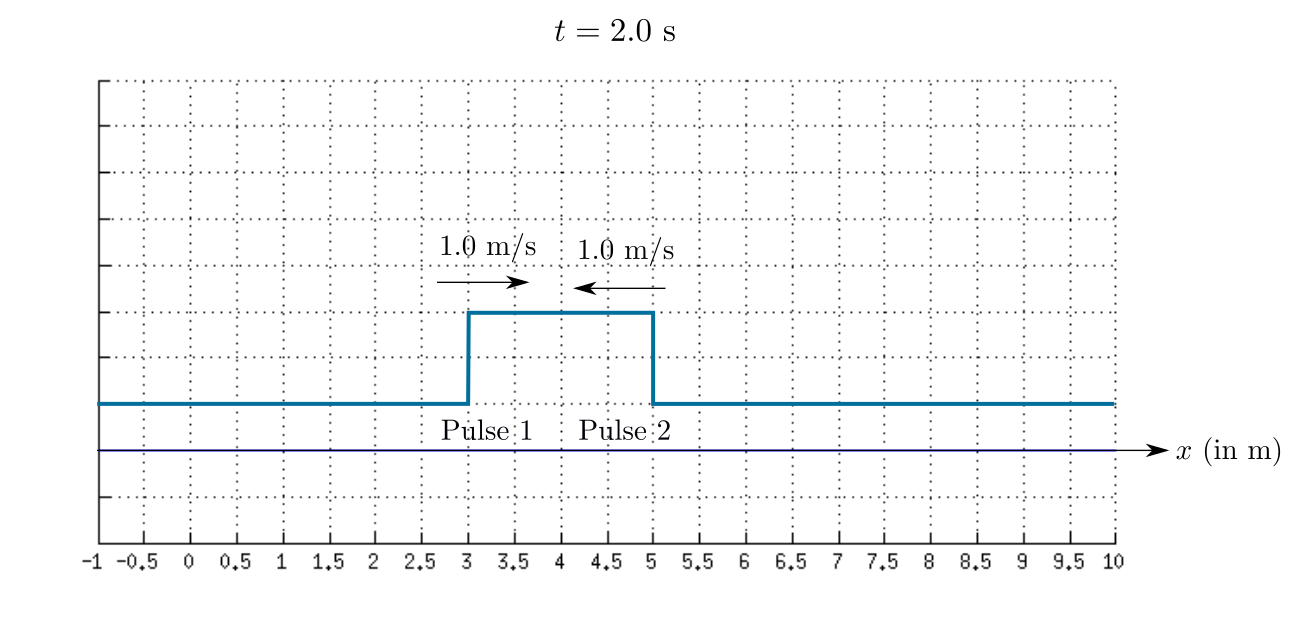
The sketch of the resultant waves at $t=2.0$ s is shown in the given figure.

In this graph, both the pulses are side by side (but not meeting). Therefore, the width of the resultant pulse has increased.

Exercise scan

Step 4

4 of 7

$$
textbf{(c)}
$$

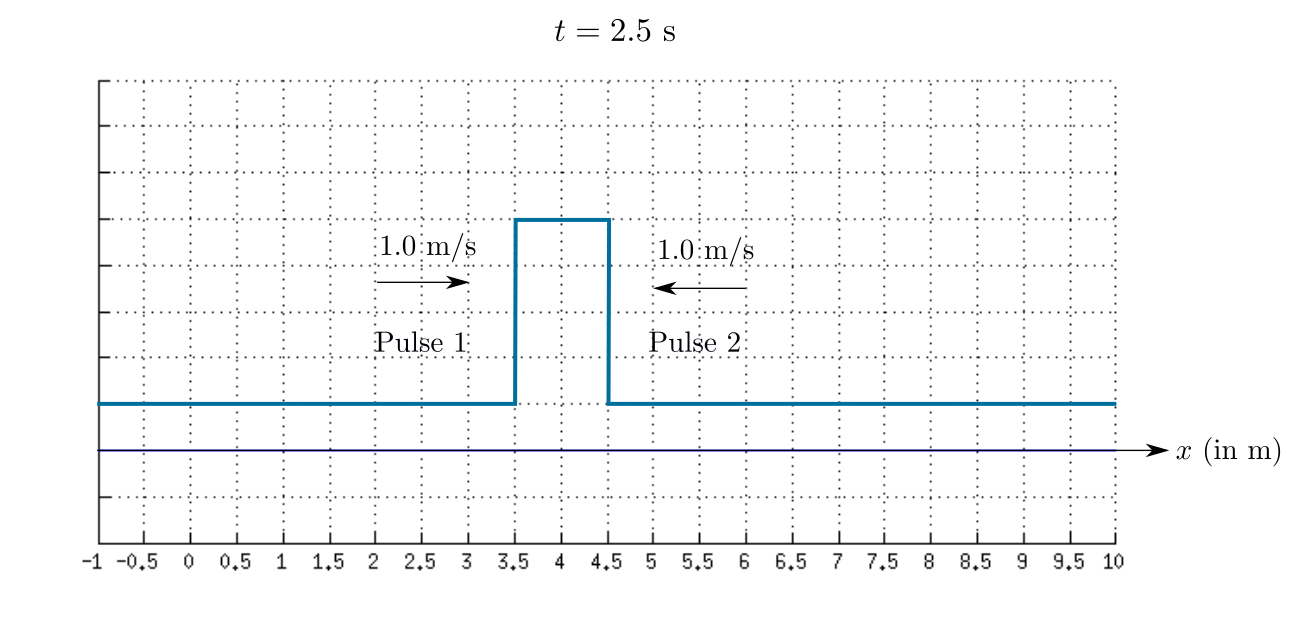
The sketch of the resultant waves at $t=2.5$ s is shown in the given figure.

In this graph, both the pulses are exactly meeting each other. Therefore, the height of the resultant pulse has increased but the width is the same.

Exercise scan

Step 5

5 of 7

$$
textbf{(d)}
$$

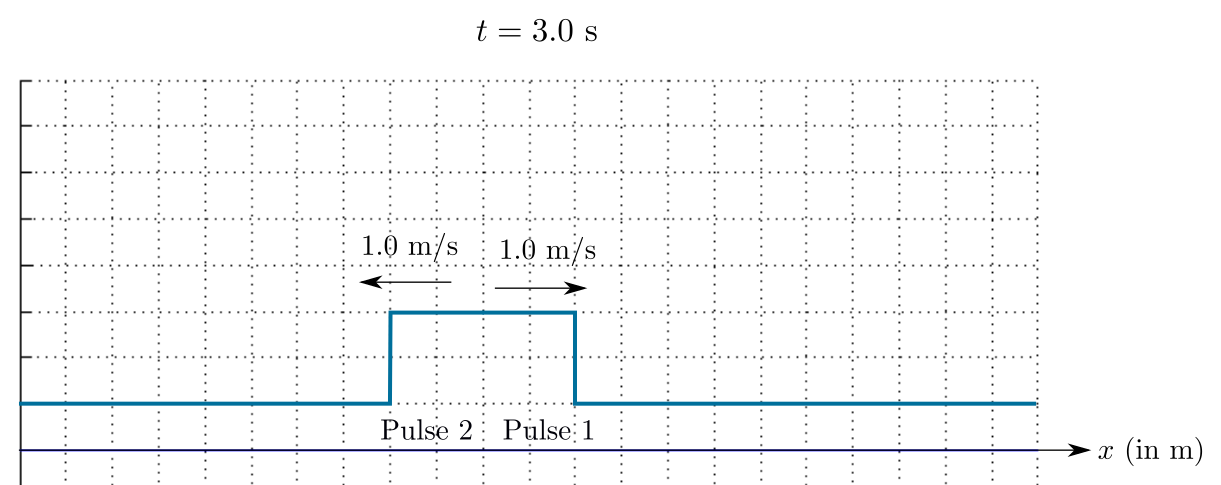
The sketch of the resultant waves at $t=3.0$ s is shown in the given figure.

In this graph, both the pulses are side by side (but not meeting). Therefore, the width of the resultant pulse has increased.

Exercise scan

Step 6

6 of 7

$$
textbf{(e)}
$$

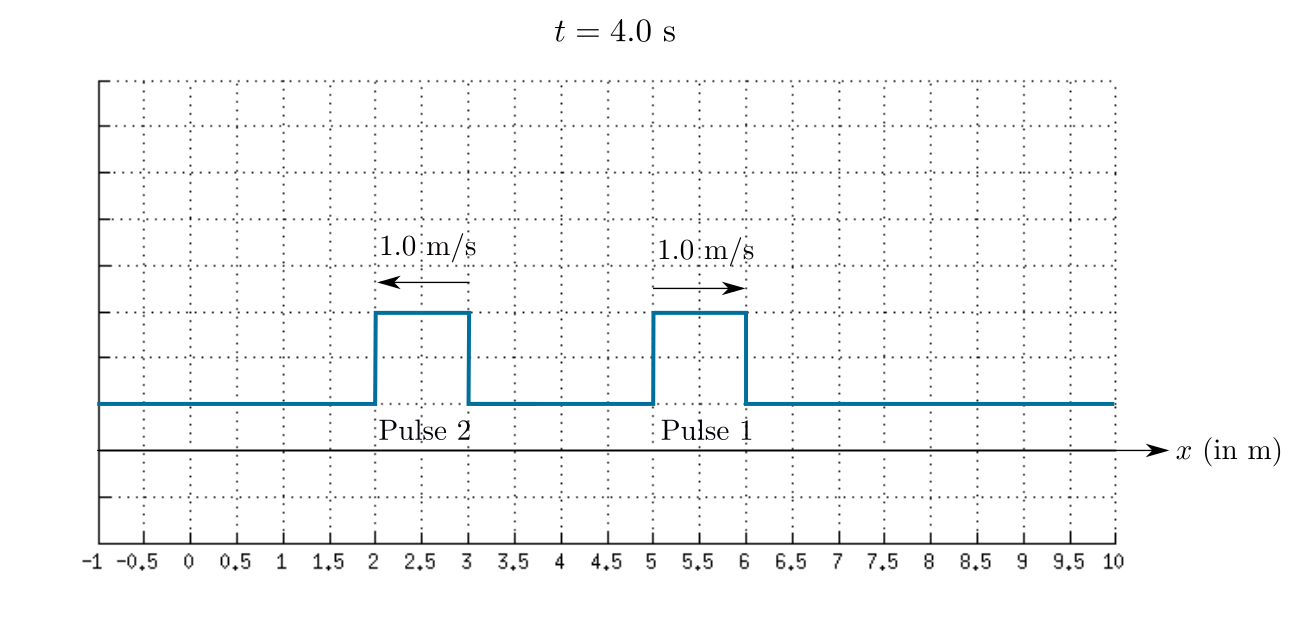
The sketch of the resultant waves at $t=4.0$ s is shown in the given figure.

In this graph, both the pulses are far from each other.

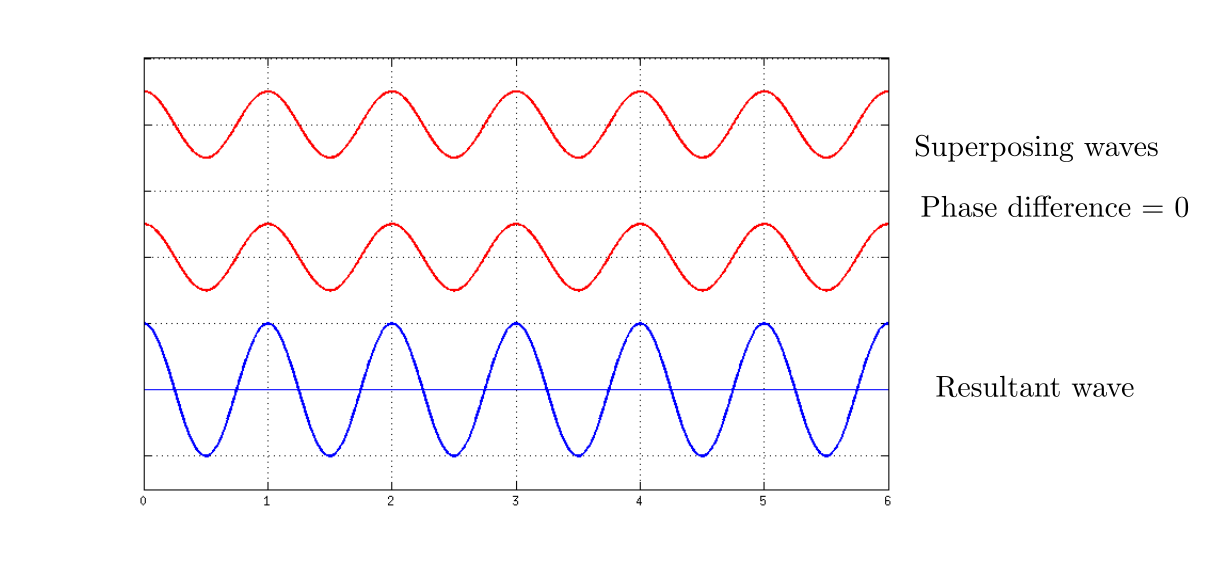
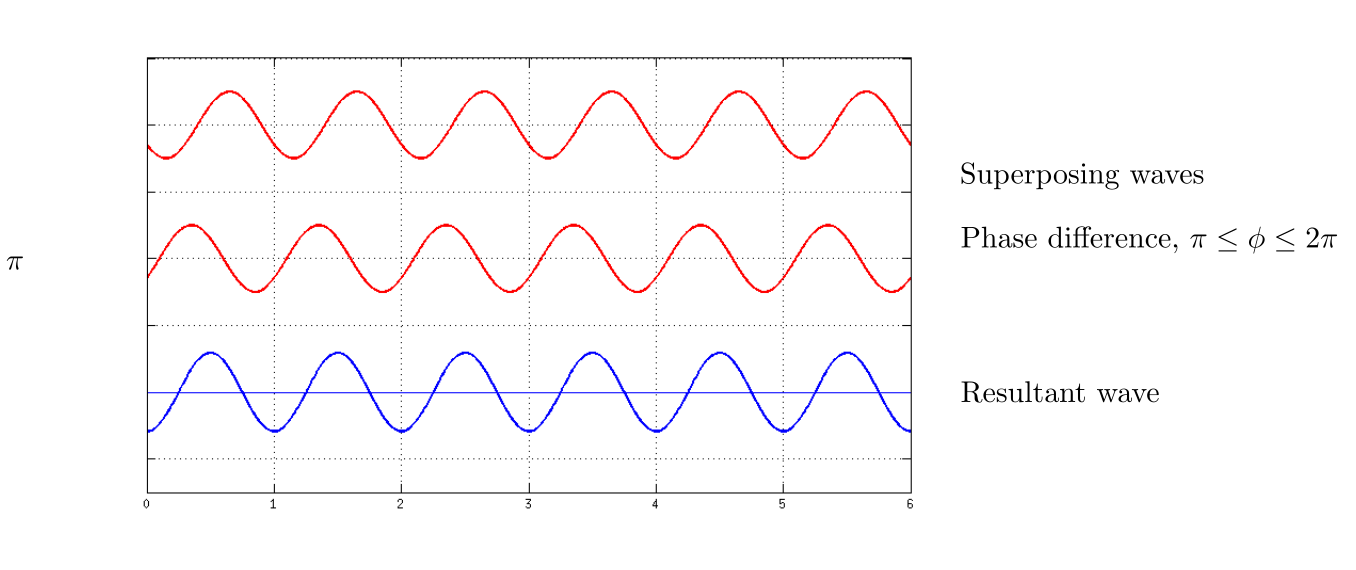
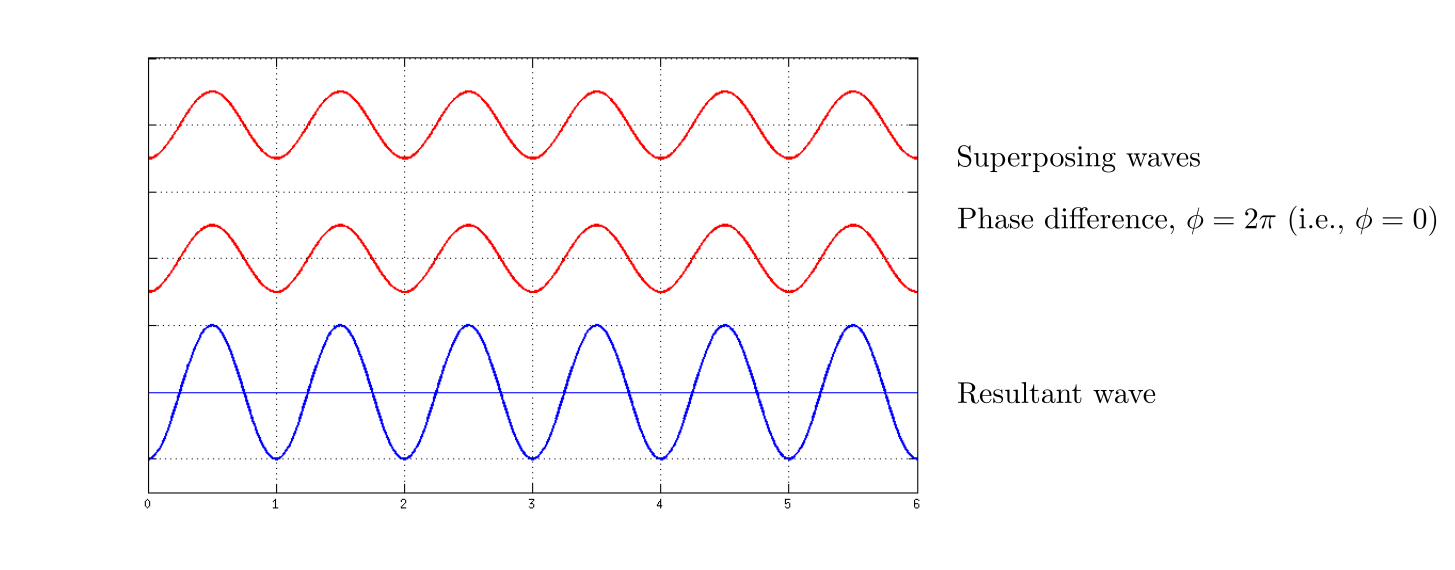
Exercise scan

Result

7 of 7

The graphs for the opposite travelling waves are shown in the given figures.

Exercise 50

Step 1

1 of 7

Yes, the classmate is correct.

Let us suppose that two waves have the same amplitude and wavelength, and they interfere with each other.
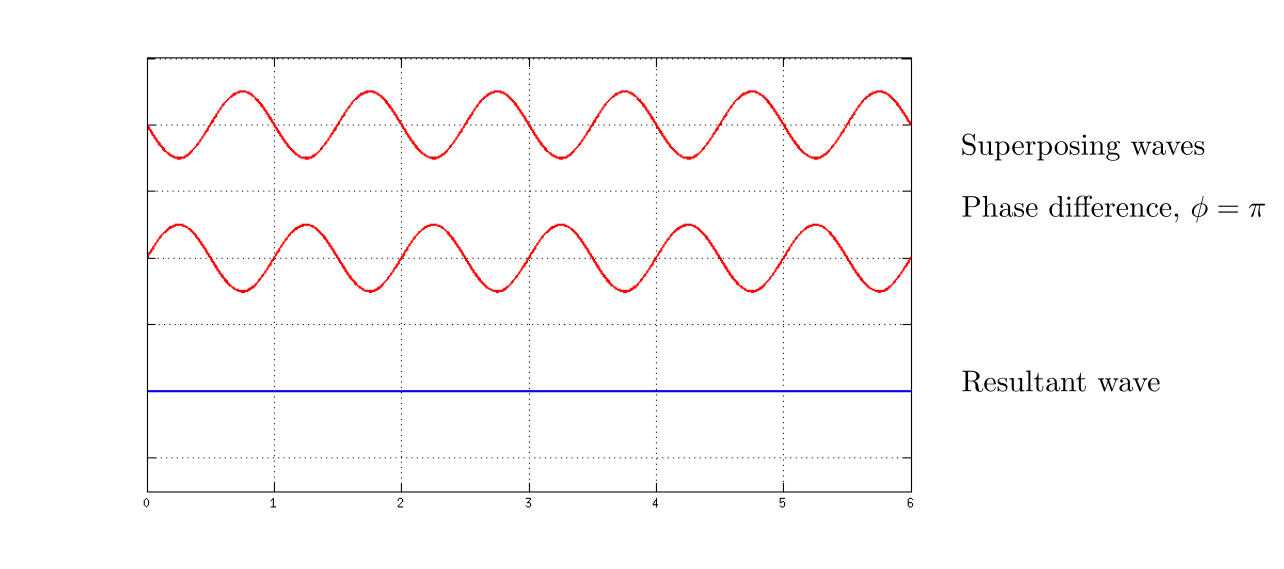
If these two waves have the same phase they interfere constructively. If they have $phi = pi$ phase difference than they interfere destructively.

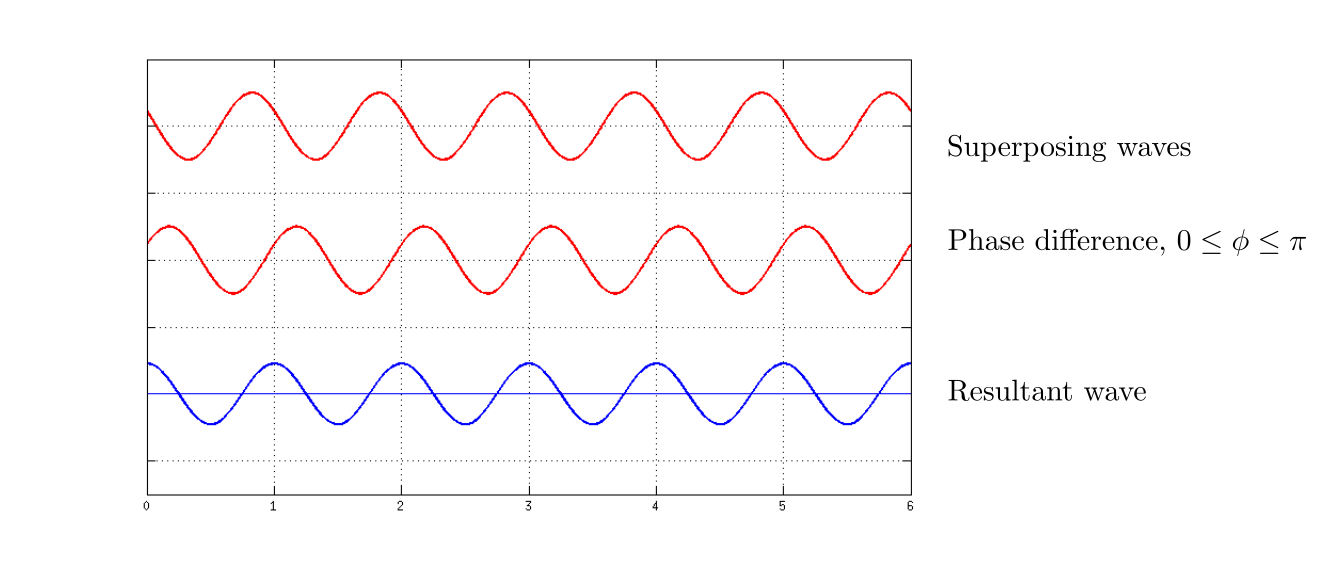
All the phases between zero to $2pi$ give a resultant wave with different amplitudes. Hence, we see a wave having amplitude from minimum to maximum (or maximum to minimum) at the same place. Therefore, we see a standing wave.

Hence, a standing wave involves both constructive and destructive interference which can be seen in the given graphs.

Step 2

2 of 7

The first graph shows the interference of the two waves when phase difference is zero. Exercise scan

Step 3

3 of 7

The second graph shows the interference of the two waves when phase difference is $0le phi le pi$.

Exercise scan

Step 4

4 of 7

The third graph shows the interference of the two waves when phase difference is $phi = pi$.

Exercise scan

Step 5

5 of 7

The fourth graph shows the interference of the two waves when phase difference is $pile phi le 2pi$.

Exercise scan

Step 6

6 of 7

The fifth graph shows the interference of the two waves when phase difference is $phi = 2pi$.

Exercise scan

Result

7 of 7

Yes, the classmate is correct.

Exercise 52

Solution 1

Solution 2

Step 1

1 of 1

Higher the harmonic, higher the number of nodes (and so anti-nodes) and hence shorter wavelength. Since f = $dfrac{v}{wavelegth}$

we get, lower the wavelegth, higher is the frequency.

In short,yes,higher harmonics always have greater frequencies than lower harmonics

Step 1

1 of 2

As shown in the given figure, the fundamental mode (first harmonic) corresponds to half a wavelength of a
usual wave on a string.

The second harmonic consists of two half wavelengths of the wave.

The third harmonic consists of three half wavelengths of the wave and so on.

Therefore, the corresponding frequencies of higher harmonics are higher than that of lower harmonics.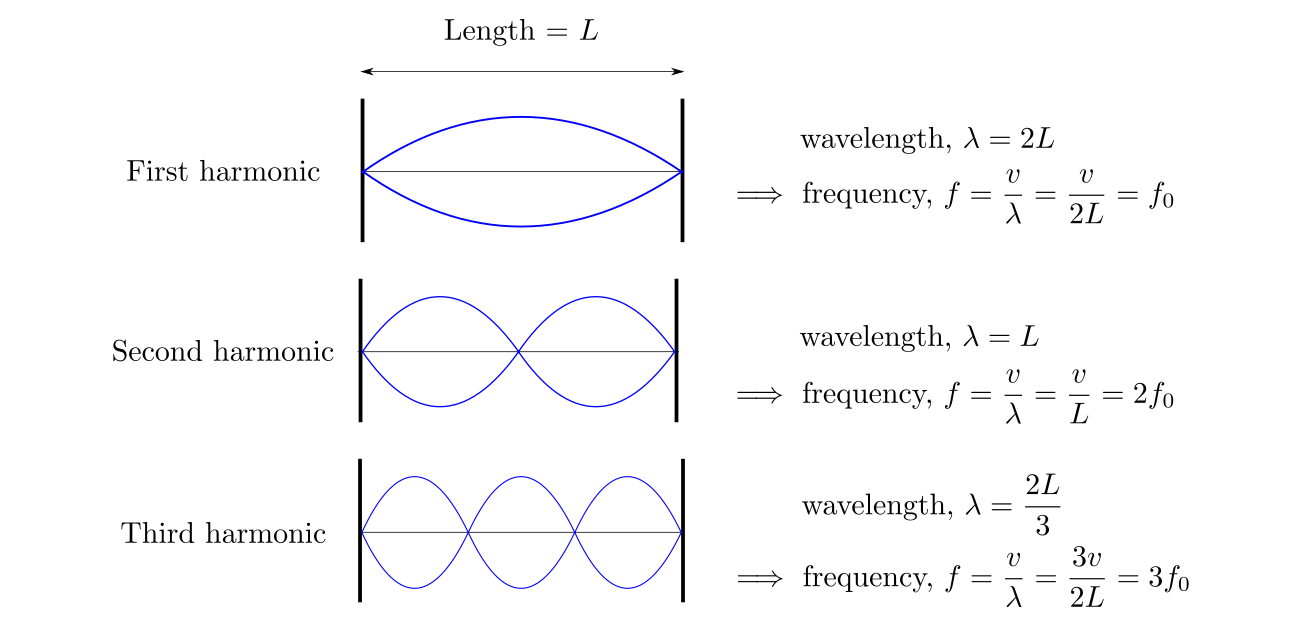 Exercise scan

Result

2 of 2

Yes.

Exercise 53

Solution 1

Solution 2

Step 1

1 of 3

$textbf{(a)}$
A guitar makes standing waves with nodes at the ends.

In the given figure, we see that–

The fundamental mode (first harmonic) is shown which has two nodes and one antinode.

The second harmonic has three nodes and two antinodes.

The third harmonic has four nodes and three antinodes.

Therefore, the vibrating guitar with two antinodes has second harmonic.

Exercise scan

Step 2

2 of 3

$textbf{(b)}$ The length of the string is given as

$$
begin{align*}
L & = 66 mathrm{cm}
end{align*}
$$

As shown in the given figure, the second harmonic has wavelength equal to the length of the string.

Therefore, the wavelength of the wave is

$$
begin{align*}
lambda & = L \
lambda & = 66 mathrm{cm} \
& hspace*{-3mm}boxed{lambda = 66 mathrm{cm} }
end{align*}
$$

Exercise scan

Result

3 of 3

(a) Second harmonic.

(b) ${lambda = 66 mathrm{cm} }$

Step 1

1 of 2

begin{enumerate}[a)]
item
The standing wave the guitar vibrates with has two antinodes. \
If it had one antinode it would have been the first harmonic, since it has two we conclude that this is the second harmonic.
item
For the second harmonic we know that one whole wavelength will fit across the string, that is:
begin{align*}
lambda = L = 66text{ cm}
end{align*}
end{enumerate}

Result

2 of 2

begin{enumerate}[a)]
item
The second harmonic
item
The wavelength is $lambda = 66text{ cm}$
end{enumerate}

Exercise 54

Step 1

1 of 2

We know that when a standing wave is formed in a string the number of antinodes determines the harmonic of the wave. This gives us a result that the length of the string is equal to a integer number of wavelength halves, that is:
begin{align*}
L = n cdot frac{lambda}{2}
end{align*}
Since the length of the string is $ L = 33text{ cm}$ we get:
begin{align*}
2 cdot L = 2 cdot 33text{ cm} = 66text{ cm} = n cdot lambda
end{align*}
From this we see that any wavelength $lambda$ that fulfils this equation for an integer $n$ can produce a standing wave. \
begin{enumerate}[For]
item
$lambda_1 = 0.22text{ m}$ we get $n_1 = frac{66text{cm}}{22text{ cm}} = 3$
item
$lambda_2 = 0.33text{ m}$ we get $n_2 = frac{66text{cm}}{33text{ cm}} = 2$
item
$lambda_3 = 0.44text{ m}$ we get $n_3 = frac{66text{cm}}{44text{ cm}} = 1.5$
item
$lambda_4 = 0.66text{ m}$ we get $n_4 = frac{66text{cm}}{66text{ cm}} = 1$
end{enumerate}
Since $n_1$ , $n_2$ and $n_4$ are integers all of these wavelengths $lambda_1 , lambda_2 , lambda_4$ form standing waves. \\
These are actually the third, second and first harmonics.

Result

2 of 2

The first, second and third wavelengths form the third, second and first harmonics

Exercise 55

Step 1

1 of 2

We know that for the first harmonic only half a wavelength fits on a string. Therefore we can write:

$$
begin{align*}
L = frac{lambda}{2}
end{align*}
$$

Plugging in the value for the wavelength of the first harmonic $lambda = 0.65text{ m}$ we get:

$$
begin{align*}
L = frac{0.65text{ m}}{2} = 0.325text{ m}
end{align*}
$$

Result

2 of 2

The distance between the walls is $L = 0.325text{ m}$

unlock

All Solutions

Page 482: Lesson Check

Haven't found what you were looking for?

Search for samples, answers to your questions and flashcards