
All Solutions
Page 810: Assessment
Since the magnetic field of a bar magnet points towards the south pole of the bar magnet, Earth’s magnetic field points into the Earth’s surface near the north geographical pole.
Field lines could never cross, they would not only want to be pointing at two different directions, whether they would point as a resultant vector sum of those two directions. The compass needle is always pointing north of Earth (south magnetic pole). Magnetic field lines come outside of the south pole and get into the north pole, they $textbf{never intersect}$ and the compass needle acts always as a tangent. In other words, they form an endless loop.
One more argument for this is that we always have a magnetic dipole, there are no such things as a magnetic monopole
If magnetic field lines cross then at the point of intersection, magnetic field points in two directions which is impossible.
So magnetic field lines do not cross.
They form closed loop.
In a bar magnet, magnetic field lines enter the magnet at south pole and leaves the magnet at north pole.
Their size varies from $10^{-4} mathrm{~cm}$ to $10^{-1} mathrm{~cm}$. Before the external magnetic field, we can simplify the model with the following picture:

Magnetism has a significant role in the proof of this because Earth’s magnetic fields have reversed it more than few times in the past.
After the volcanos erupt they get into the ocean and cool down, since they get into the solid state of matter, they do become permanently magnetized in the direction of the Earth’s magnetic field.
Now, this is explored by paleomagnetism, when we analyze the seafloor and the pattern. We see the ridges in the seafloor pattern changing on a specific location. This clearly indicated that when there is a change of ridge patterns is due to the change of Earth’s magnetic field, because magnetization changes. We also see this relative to the direction on the side, which supports the evidence for continental drift. As we can see the seafloor is expanding in time due to the pattern, which indicates the continental drift.
As a result, magnetic field is intense in one side and on the other side it is weak. So the side with intense field stick to the refrigerator and the other side does not.
When a bar magnet is suspended its north pole points towards Earth’s north geographical pole or south pole of Earth’s magnet.
So in region 1, magnitude of magnetic field is larger.
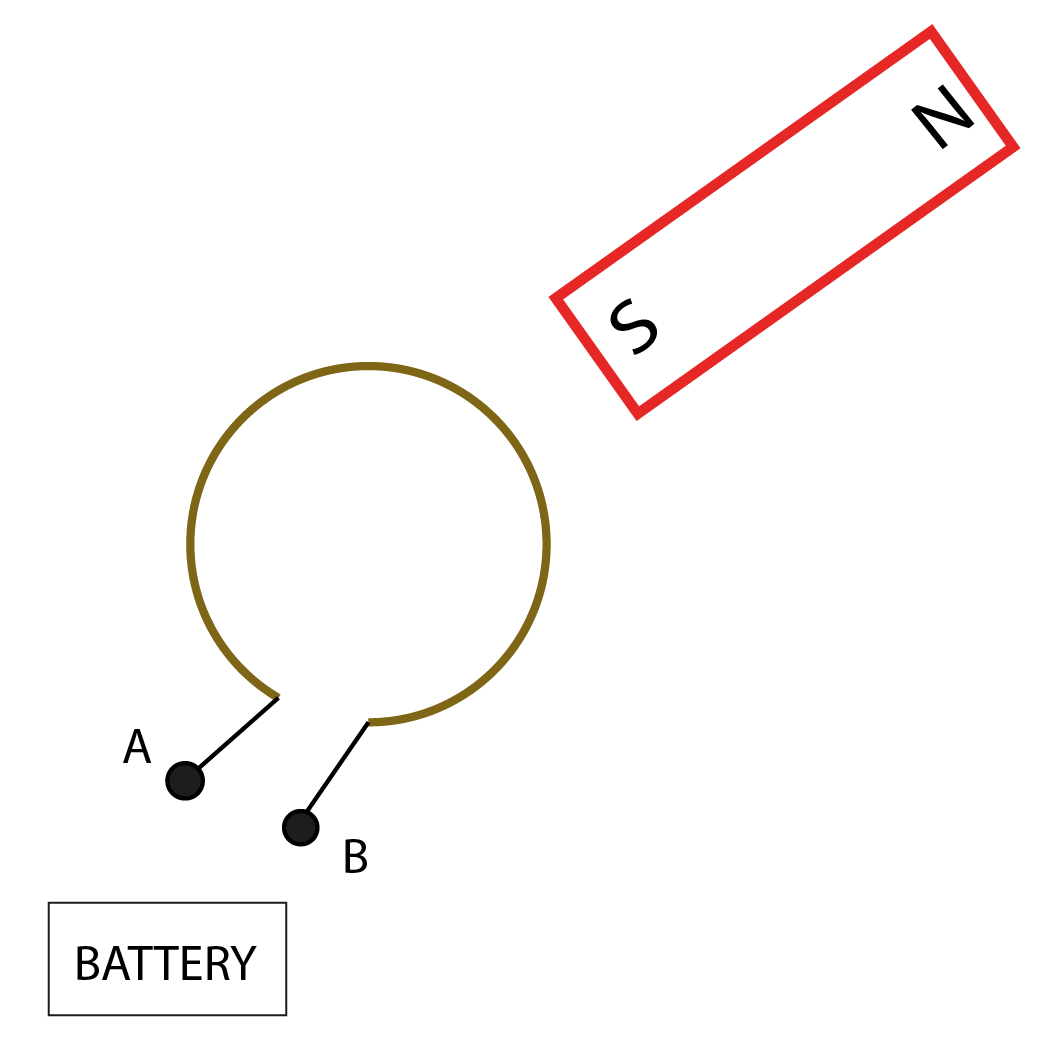
To have that, we also remember that the magnetic field is going outside of the north pole, and getting into the south pole. So, by the right-hand rule to have this situation, we want current to flow $textbf{terminal A to the terminal B}$, in other words, we would like for terminal A to be connected to the positive pole of the battery.
We know that current is by convention flowing from the positive to the negative pole of the battery.
$$
B=mu_{0}left(frac{N}{L}right) I
$$
where N is exactly the number of the loops of the solenoid and N is the length of the solenoid, or commonly we also call $frac{N}{L}$ number of the loops per length.
Regarding the $textbf{part b}$ we can see that the explanation C is the best fitting, considering the arguments said above:
$$
textit{C The magnetic field remains the same because the number of loops per length is unchanged.}
$$
(b) C
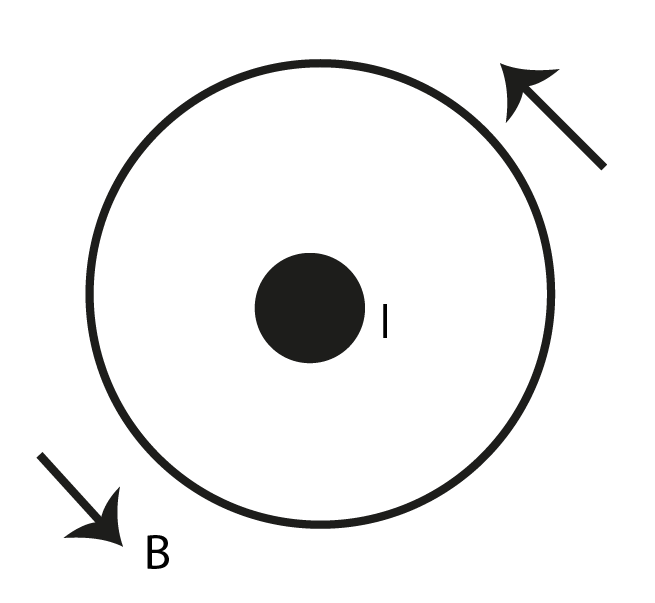
We point our fingers in the direction of current and the thumb is going to show the direction of the magnetic field. The other way around is also working. The thumb in the direction of the magnetic field (out of the page) and the fingers are going to show the direction of the current, which for this case is counterclockwise.
$$
B=1 {rm T}=frac{mu_{0}I_{0}}{2pi r_{0}}
$$
1. When current is $2I_{0}$ and distance is $r_{0}$, we have
$$
B_{1}=frac{mu_{0}left(2I_{0}right)}{2pi r_{0}}=2left(frac{mu_{0}I_{0}}{2pi r_{0}}right)=2 {rm T}
$$
2. When the current is $2I_{0}$ and the distance is $2r_{0}$, then
we have
$$
B_{2}=frac{mu_{0}I_{0}}{2pileft(2r_{0}right)}=frac{1}{2}left(frac{mu_{0}I_{0}}{2pi r_{0}}right)=0.5 {rm T}
$$
3. When the current is $4I_{0}$ and the distance is $4r_{0}$, then
we have
$$
B_{3}=frac{mu_{0}left(4I_{0}right)}{2pileft(4r_{0}right)}=frac{4}{4}left(frac{mu_{0}I_{0}}{2pi r_{0}}right)=1 {rm T}
$$
$B = dfrac{mu_0 I}{2 pi r}$; where $mu_0 = 4 pi times 10^{-7} : T.m.A^{-1}$.
$B = dfrac{^2cancel{4 pi} times 10^{-7} times I}{cancel{2 pi} r} = dfrac{2 times 10^{-7} times I}{r}$
So the magnetic field produced by a straight wire carrying $5.6:A$ current at a radial distance of $0.22:m$ is
$B = dfrac{2 times 10^{-7} times 5.6}{0.22} = 51 times 10^{-7}:T$
$B = dfrac{mu_0 I}{2 pi r}$; where $mu_0 = 4 pi times 10^{-7}:T.m.A^{-1}$
$B = dfrac{^2 cancel{4 pi} times 10^{-7} times I}{cancel{2 pi} r} = dfrac{2 times 10^{-7} times I}{r}$
Current required to produce a magnetic field of $6.1 times 10^{-6}:T$ at a radial distance of $26:cm = 0.26 :m$ is
$I = dfrac{Br}{2 times 10^{-7}} = dfrac{Br}{2} times 10^7 = dfrac{6.1 times 10^{-6} times 0.26}{2} times 10^7 = 7.93:A$
$B = dfrac{mu_0 I}{2 pi r}$; where $mu_0 = 4 pi times 10^{-7}:T.m.A^{-1}$
$B = dfrac{^2 cancel{4 pi} times 10^{-7} times I}{cancel{2 pi} r} = dfrac{2 times 10^{-7} times I}{r}$
The radial distance at which current of $8.6:A$ produces a magnetic field of $3.3 times 10^{-5}:T$ is given by
$r = dfrac{2 times 10^{-7} times I}{B} = dfrac{2 times 10^{-7} times 8.6}{3.3 times 10^{-5}} =5.2 times 10^{-2}:m = 5.2:cm$
$B = mu_0 times dfrac{N}{L} times I$
where $mu_0 = 4 pi times 10^{-7} :T.m.A^{-1}$
Number of loops required to produce a magnetic field of $0.78:T$ inside a solenoid of length $32:cm = 0.32:m$ carrying $7.7:A$ current is
$N = dfrac{B L}{mu_0 I} = dfrac{0.78 times 0.32}{4 pi times 10^{-7} times 7.7} =0.00257955 times 10^7 = 25796:loops$
$B = mu_0 times dfrac{N}{L} times I$
where $mu_0 = 4 pi times 10^{-7} :T.m.A^{-1}$
Given data are
$dfrac{N}{L} = 1200$ and $I =6.8:A$
So, $B = 4pi times 10^{-7} times 1200 times 6.8 = 102.5 times 10^{-4} :T$
$B = dfrac{mu_0 I}{2 pi r}$; where $mu_0 = 4pi times 10^{-7}:T.m.A^{-1}$
$B = dfrac{^2cancel{4pi} times 10^{-7} times I}{cancel{2 pi} r} = dfrac{2 times 10^{-7} times I}{r}$
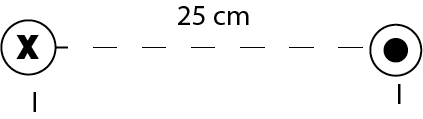
Half of the Earth’s magnetic field is $dfrac{5.0 times 10^{-5}}{2} = 2.5 times 10^{-5}:T$
The current required to produce this field at a radial distance of $0.25:m$ is given by
$I = dfrac{Br}{2 times 10^{-7}} = dfrac{Br}{2} times 10^7 = dfrac{2.5 times 10^{-5} times 0.25}{2} times 10^7 = 31.25:A$
$B = dfrac{mu_0 I}{2 pi r}$; where $mu_0 = 4pi times 10^{-7}:T.m.A^{-1}$
$B = dfrac{^2cancel{4pi} times 10^{-7} times I}{cancel{2 pi} r} = dfrac{2 times 10^{-7} times I}{r}$
The radial distance, at which a long straight wire carrying $3.6:A$ current produces a magnetic field of $3.5 times 10^{-5}:T$, is given by
$r = dfrac{2 times 10^{-7} times I}{B} = dfrac{2 times 10^{-7} times 3.6}{3.5 times 10^{-5}} = 2.1 times 10^{-2}:m = 2.1:cm$
$B = dfrac{mu_0 I}{2 pi r}$; where $mu_0 = 4pi times 10^{-7}:T.m.A^{-1}$
$B = dfrac{^2cancel{4pi} times 10^{-7} times I}{cancel{2 pi} r} = dfrac{2 times 10^{-7} times I}{r}$
The current required to produce magnetic field of $5.0 times 10^{-4}:T$ at a distance of $0.50:m$ is given by
$I = dfrac{Br}{2 times 10^{-7}} = dfrac{Br}{2} times 10^7 = dfrac{5.0 times 10^{-4} times 0.50}{2} times 10^7 = 1250:A$
wire are in same direction, while the magnetic field produced by at
B are in opposite direction. Hence the magnitude of the magnetic field
will be higher at A than B.
(b) Magnetic field at A is
$$
B_{A}=frac{mu_{0}I_{x}}{2pi r_{x}}+frac{mu_{0}I_{y}}{2pi r_{y}}=frac{left(1.26times10^{-6} {rm m,kg,s^{-2}A^{-2}}right)left(6.2 {rm A}right)}{2pileft(0.16 {rm m}right)}+frac{left(1.26times10^{-6} {rm m,kg,s^{-2}A^{-2}}right)left(4.5 {rm A}right)}{2pileft(0.16 {rm m}right)}=1.3times10^{-5} {rm T}
$$
And magnetic field at B is
$$
B_{B}=frac{mu_{0}I_{x}}{2pi r_{x}}-frac{mu_{0}I_{y}}{2pi r_{y}}=frac{left(1.26times10^{-6} {rm m,kg,s^{-2}A^{-2}}right)left(6.2 {rm A}right)}{2pileft(0.16 {rm m}right)}-frac{left(1.26times10^{-6} {rm m,kg,s^{-2}A^{-2}}right)left(4.5 {rm A}right)}{2pileft(0.16 {rm m}right)}=2.1times10^{-6} {rm T}
$$
$$
B=frac{mu_{0} I}{2 pi r}
$$
where r is the radial distance at the center, which is going to be here half of the distance, which is 12.5 cm. So putting in the numbers we have:
$$
B = frac{left(1.26 times 10^{-6} mathrm{~kg} mathrm{~m} mathrm{~s}^{2} mathrm{~A}^{-2}right)(11 mathrm{~A})}{2 pi(0.125 mathrm{~m})}
$$
which gives the result of:
$$
B=1.77 times 10^{-5} mathrm{~T}
$$
Since the magnetic fields doubles, due to both wires, the total field will be:
$$
B_{tot} = 2 cdot 1.77 times 10^{-5} mathrm{~T} = boxed{color{#c34632}3.53 times 10^{-5} mathrm{~T}}
$$
B_{tot} = 3.53 times 10^{-5} mathrm{~T}
$$

$$
B=frac{mu_{0} I}{2 pi r}
$$
From the relation we can see that field is proportional to the current, so the current on the left is going to produce a stronger field, than the current on the right. So, the total field is going to point upward (determined by the right-hand rule). The $r$, which is the radius is going to be half the distance, which is 6.1 cm. So putting in the numbers for the wire on the left, we got:
$$
B=frac{left(1.26 times 10^{-6} mathrm{~kg} mathrm{~m} mathrm{~s}^{2} mathrm{~A}^{-2}right)(4.33 mathrm{~A})}{2 pi(0.061 mathrm{~m})}
$$
which gives the result of:
$$
B=3.62 times 10^{-5} mathrm{~T}
$$
For the wire on the right we repeat the same calculation, only we change the current magnitude:
$$
B=frac{left(1.26 times 10^{-6} mathrm{~kg} mathrm{~m} mathrm{~s}^{2} mathrm{~A}^{-2}right)(2.75 mathrm{~A})}{2 pi(0.061 mathrm{~m})}
$$
which gives the result of:
$$
B=9.05 times 10^{-6} mathrm{~T}
$$
$$
B _{tot} = B_{left} – B_{right}
$$
Putting in the numbers we have:
$$
B _{tot} = 3.62 times 10^{-5} mathrm{~T} – 9.05 times 10^{-6} mathrm{~T}
$$
which gives the result of:
$$
boxed{color{#c34632}B _{tot} = 2.72 times 10^{-5} mathrm{~T}}
$$
B _{tot} = 2.72 times 10^{-5} mathrm{~T}
$$
$B = mu_0 times dfrac{N}{L} times I$
where $mu_0 = 4 pi times 10^{-7} :T.m.A^{-1}$
Number of loops required to produce a magnetic field of $0.25:T$ inside a solenoid of length $55:cm = 0.55:m$ carrying $2.0:A$ current is given by
$N = dfrac{B L}{mu_0 I} = dfrac{0.25 times 0.55}{4 pi times 10^{-7} times 2.0} = 54710:loops$
Length of one loop $=2 pi r$ (Circumference of the loop)
where $r = dfrac{12}{2} = 6:cm$
Length of one loop $=2 pi times 6 = 37.7:cm$
Length of 54710 loops $= 54710 times 37.7 = 20:62:567:cm =20:626:m$
Total length of the wire required is $20:626:m$.
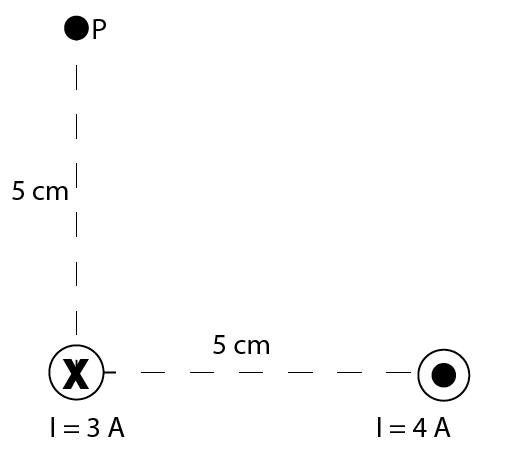
$$
B=frac{mu_{0} I}{2 pi r}
$$
For the wire on the left, $r$ is simply 5 cm, so we have:
$$
B=frac{left(1.26 times 10^{-6} mathrm{~kg} mathrm{~m} mathrm{~s}^{2} mathrm{~A}^{-2}right)(3 mathrm{~A})}{2 pi(0.05 mathrm{~m})}
$$
which gives the result of:
$$
B_1=1.2 times 10^{-5} mathrm{~T}
$$
For the field due to the wire on the right, we first need to calculate the radius. Since in the picture, we can see both of them it 5 cm in both direction by Pythagorean theorem:
$$
r = sqrt{5^{2}+5^{2}}= sqrt{50} = 7.07 mathrm{~cm}=0.07 mathrm{~m}
$$
So for the magnetic field from the wire on the right we have:
$$
B=frac{left(1.26 times 10^{-6} mathrm{~kg} mathrm{~m} mathrm{~s}^{2} mathrm{~A}^{-2}right)(4 mathrm{~A})}{2 pi(0.07 mathrm{~m})}
$$
we have a result of:
$$
B_2=1.15 times 10^{-5} mathrm{~T}
$$
$$
B_{2}=-B_{2} cos 45 -hat{x}-B_{2} sin 45 -hat{y}
$$
The angles are simply coming out from that we have a nice triangle of 45-45-90 degrees. Putting in the sin and cos we have:
$$
B_{2}=0.81 times 10^{-5}hat{x}+0.81 times 10^{-5} -hat{y}
$$
Now we can calculate the total field, which is:
$$
B_{text {tot }}=B_{1}+B_{2}
$$
Putting the numbers and unit vectors we have:
$$
B_{text {tot }}=1.2 times 10^{-5}hat{x}+left(0.81 times 10^{-5}hat{x}-0.81 times 10^{-5} hat{y}right)
$$
which gives:
$$
B_{text {tot }}=4 times 10^{-6} -0.81 times 10^{-5} j
$$
to get the magnitude, we calculate the norm (square of it), so we have:
$$
B_{t o t}=sqrt{left.left(4 times 10^{-6}right)^{2}+left(0.81 times 10^{-5}right)^{2}right]}
$$
which gives the result for the magnitude:
$$
B_{t o t}= 9.03 times 10^{-6} mathrm{~T}
$$
$$
tan theta = frac{B_y}{B_x}
$$
to get the angle we have:
$$
theta= tan^{-1} frac{0.81 times 10^{-5}} {4 times 10^{-6}}
$$
we get the angle of:
$$
theta= 63.71 ^{circ}
$$
and direction is with this angle, below the horizontal.
B_{t o t}= 9.03 times 10^{-6} mathrm{~T}, theta= 63.71 ^{circ} text{below horizontal}
$$
$vec{F} = q (vec{v} times vec{B})$
Suppose two charged particles moving with same velocity $vec{v}$ in magnetic field $vec{B}$ are deflected in opposite directions, then the magnetic force acting on them is opposite to each other.
From the force equation, it is possible only if the particles have opposite charges.
$F = IBL sin theta$
where $theta$ is the angle between the direction of the magnetic field and the wire.
If, $theta = 0^o$, then $sin 0^o = 0$ and consequently the magnetic force on the wire is zero.
So if the wire is placed in the direction of magnetic field, so that $theta = 0^o$, the magnetic force on the wire becomes zero.
The magnitude of the magnetic force can be calculated with the following relation:
$$
F=|q| v B sin theta
$$
where $theta$ is exactly the angle between the speed vector and the magnetic field. Since we know that sine of 0 degrees is zero, so if the speed and magnetic field vector point in the same direction (parallel or antiparallel) the force will be zero.
Also, we know that Earths’ magnetic field is pointing from the south to the north pole. From this said, we can see that angle for proton one will be equal almost to the right angle, and the angle for proton 2 will be equal almost to zero (or very close).
So for the $textbf{part a}$ magnetic field due to the Earth’s magnetic field is much higher for the proton 1.
Regarding the $textbf{part b}$ the correct statement is:
$$
textit{B. Proton 1 experiences the greater force because it
moves at right angles to the magnetic field.}
$$
(b) B.
$vec{F} = q (vec{v} times vec{B})$
From this equation it is obvious that the force vector $vec{F}$ is always perpendicular to the plane containing the velocity vector $vec{v}$ and the magnetic field vector $vec{B}$.
If an electron moves in the positive $x$ direction (that is,$vec{v}$ points in the positive $x$ direction) and it experiences force in the positive $y$ direction, then the magnetic field vector must lie in the $x-z$ plane,
If the magnitude of the force experienced by the electron is maximum then $vec{v}$ and $vec{B}$ must be perpendicular to each other. So in this case, the magnetic field $vec{B}$ points in the negative $z$ direction. This is because the charge of the electron is negative.
$$
v_c<v_b<v_a
$$
The trajectories of the particles A and B are in the direction given by right hand rule. So they are positively charged.
Particle C moves in the direction opposite to that of prescribed by right hand rule. So it is negatively charged.
is in teh negative $y$ direction. And the magnetic field is from
left to right, hence $vec{B}$ is in positive $x$ direction. and
the charge of the elctron is given by $-e$. Hence the force on the
electron is given by
$$
-evec{v}timesvec{B}
$$
So the direction will be down wards. Henc the left side will be north
pole, only then the magnetic field will be in positive $x$ direction.
$F = IBL sin theta$
If $F=1.6:N$, $L=1.2:m$, $I=3.0:A$ and $B = 0.50:T$ then
$sin theta = dfrac{F}{IBL} = dfrac{1.6}{1.2 times 0.5 times 3} = 0.89$
$theta = sin^{-1}(0.889) = 62.7^o$
So the angle between the magnetic field and the wire is $62.7^o$.
theta = 62.7^o
$$
Its speed is given as $v = 350:m/s$.
The magnitude of the magnetic field is given as $B = 4.1 times 10^{-5}:T$
The angle between the direction of the magnetic field and the direction of motion of proton is, $theta = 90^o$.
So the magnitude of the magnetic force on the proton is given by
$F = evB sintheta = 1.6 times 10^{-19} times 350 times 4.1 times 10^{-5} times sin 90^o$
$F = 2.3 times 10^{-21}:N$
$F = qvB sin theta$
If $0.95:T$ magnetic field exerts force of magnitude $4.8 times 10^{-6}:N$ on $0.32:mu C$ charge moving at speed of $16:m/s$, the angle between the magnetic field and the direction of motion of charge is given by
$sin theta = dfrac{F}{qvB} = dfrac{4.8 times cancel{10^{-6}}}{0.32 times cancel{10^{-6}} times 16 times 0.95} =0.9868421$
$theta = sin^{-1}(0.9868421) = 80.7^o$
theta = 80.7^o
$$
$F = IBL$
According to Newton’s second law of motion, the equation of motion is
$mg = IBL$
where $m$ is the mass of the wire.
So the current required to levitate the wire is given by
$I = dfrac{mg}{BL}$
Substituting the given values,
$I = dfrac{0.75 times 9.8}{0.84 times 2.7} =3.24:A$.
3.24:A
$$
$v = dfrac{qBr}{m}$
Given data are
$q=12.5 times 10^{-6}:C$, $m=2.80 times 10^{-5}:kg$, $B=1.01:T$ and $r=26.8:m$
$v = dfrac{12.5 times 10^{-6} times 1.01 times 26.8}{2.80 times 10^{-5}} = 12.08:m/s$
12.08:m/s
$$
$F = qvB sin theta$
The value of the magnetic field $B$ that exerts force of magnitude $2.2 times 10^{-4}:N$ on a charge $14 times 10^{-6}:C$ moving with speed $27:m/s$ perpendicular to the field, is given by
$B = dfrac{F}{qv sin theta} = dfrac{2.2 times 10^{-4}}{14 times 10^{-6} times 27 times sin 90^o} =0.58:B$
Force exerted by this field on the same charge moving with speed of $6.3:m/s$ at an angle $25^o$ to the magnetic field is given by
$F = 14 times 10^{-6} times 6.3 times 0.58 times sin 25^o = 21.62 times 10^{-6}:N$
21.62 times 10^{-6}:N
$$
$F = IBL$
where $I$ is the current flowing in the first power line, $L$ is the length of the first power line and $B$ is the magnetic field of the second power line.
First power line is perpendicular to the magnetic field of second power line.
Substituting the values,
$F = 110 times 8.8 times 10^{-5} times 270 = 2.6:N$
2.6:N
$$
The magnitude of the electric force is given by
$F_{ele} = qE$
where $E$ is the strength of the electric field.
The particle moves perpendicular to the magnetic field of magnitude $B$ with speed $v$. So the magnitude of the magnetic force acting on the particle is given by
$F_{mag} = qvB$
The direction of the electric force is in the dircetion of electric field, that is, along the positive $y$ direction. The direction of the magnetic force is along the negative $y$ direction. So both forces act opposite to each other.
When the total force on the particle is zero, the magnitude of electric force and magnetic force must be same. That is,
$F_{ele} = F_{mag}$
$qE = qvB$ or
$v = dfrac{E}{B}$
Substituting the value of fields,
$v = dfrac{450}{0.18} = 2500:m/s$
So the speed required to pass through the velocity selector is $2500:m/s$.
2500:m/s
$$
Its speed is given as $v = 9.1 times 10^5:m/s$.
It experiences a force of magnitude $2.0 times 10^{-13}:N$ in the negative $z$ direction, when it moves in the positive $y$ direction.
So the magnitude of the field is
$B = dfrac{F}{|e|v} = dfrac{2.0 times 10^{-13}}{1.6 times 10^{-19} times 9.1 times 10^5} = 1.37:T$
The electron experiences no force when it moves along the positive $x$ direction. This means the angle between the direction of motion of electron and the magnetic field is either $0^o$ or $180^o$.
That is, the magnetic field points either in positive $x$ direction or in negative $x$ direction.
But the electron experiences force in negative $z$ direction when it moves in positive $y$ direction. Since the electron has negative charge, the direction of the magnetic field must be along positive $x$ direction.
(b) The magnitude of the charge of the particle is $1.6 times 10^{-19}:C$. Since particle is positively charged, it is a proton.
Mass of the proton is
$$
m_p = 1.673 times 10^{-27}:kg = dfrac{1.673 times cancel{10^{-27}} :cancel{kg}}{1.67 times cancel{10^{-27}} :cancel{kg}} = 1.0017:u
$$
$$
vec{F}=qvec{v}timesvec{B}
$$
Here $q=-e$, and the velocity is in negative $z$ direction and can
be given by $vec{v}=-hat{k}v$ and magnetic field is in positive
$y$ direction and can be written as $vec{B}=hat{j}B$. So the force
is given by
$$
vec{F}=-eleft(-hat{k}vtimeshat{j}Bright)=-hat{i}evB
$$
So force will point towards west.
So according to right hand rule, the magnetic field must point into the page.
From subchapter 22.2. in the book we have a relation how to calculate the magnetic field of a current-carrying wire:
$$
B=frac{mu_{0} I}{2 pi r}
$$
Expressing the current from the previous relation we have:
$$
I=frac{2 r pi B}{mu_{0}}
$$
Putting in the information from the problem statement we have:
$$
I =frac{2 cdot 0.50 mathrm{~m} pi 1 mathrm{~T}}{1.26 times 10^{-6} mathrm{~kg} mathrm{~ms}^{-2} mathrm{~A}^{-2}}
$$
We get the result of:
$$
boxed{color{#c34632}I=2.49 times 10^{6} mathrm{~A}}
$$
I=2.49 times 10^{6} mathrm{~A}
$$
The magnetic field of the solenoid can be calculated as:
$$
B=mu_{0}left(frac{N}{L}right) I
$$
Where ratio $dfrac{N}{L}$ is exactly the number of loops per meter, where $N$ is the number of loops and $L$ is solenoid length. We can also write this ratio, as simply $n$, so we have:
$$
B=mu_{0} n I
$$
Expressing $n$ from the relation above, we have:
$$
n=frac{B}{mu_{0} I}
$$
Putting in the numbers from the problem statement we have:
$$
n = frac{17 mathrm{~T}}{1.26 times 10^{-6} mathrm{~kg} mathrm{~ms}^{-2} mathrm{~A}^{-2} cdot 105 mathrm{~A}}
$$
We get the result of:
$$
boxed{color{#c34632}n=1.28 times 10^{5} mathrm{~m}^{-1}}
$$
n=1.28 times 10^{5} mathrm{~m}^{-1}
$$
the path, then we have
$$
B_{2}>B_{1}>B_{3}
$$
the page and $B_{2}$ is into the page.
$$
m frac{v^{2}}{r}=|q| v B
$$
Expressing the radius from this we have:
$$
r=frac{m v}{|q| B}
$$
Where we can see that speed is proportional to the radius.
Regarding $textbf{part b}$ following said above we can see that the correct explanation will be:
$textit{A. The radius of a circular path in a magnetic field is proportional to the speed of the particle; therefore, the
radius of the proton’s half-circular path segments will increase.}$
(b) A
B. A greater speed means that the proton will experience more force from the magnetic field, resulting in a decrease in the radius.
$$
B=1000 {rm G}=0.1 {rm T}
$$
$$
I=2.5 {rm A}
$$
Unknown:
$r=?$
Solution:
We know that
$$
B=frac{mu_{0}I}{2pi r}
$$
So we have
$$
begin{align*}
r & =frac{mu_{0}I}{2pi B}\
& =frac{left(1.26times10^{-6} {rm kgms^{-2}A^{-2}}right)left(2.5 {rm A}right)}{1pileft(0.1 {rm T}right)}\
& =1.00times10^{-5} {rm m}=10.0 {rm mu m}
end{align*}
$$
The credit card can be brought to the 10 $mu$m close to the wire
without damaging the strip.
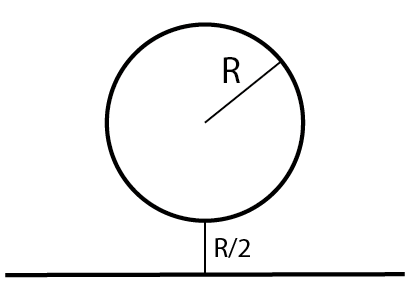
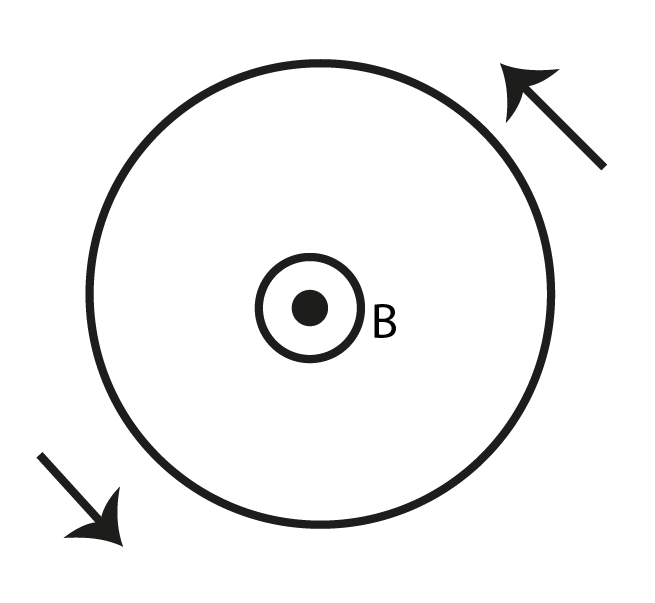
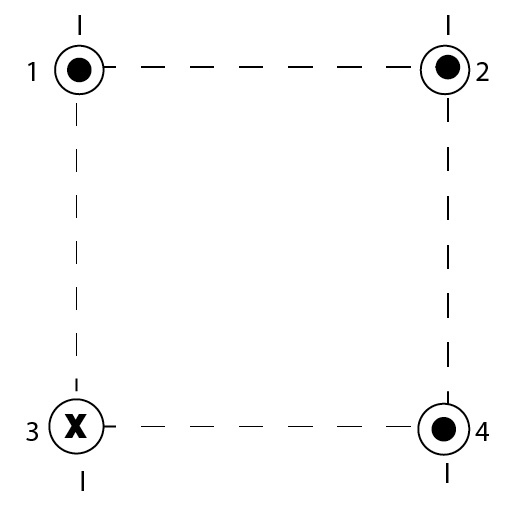
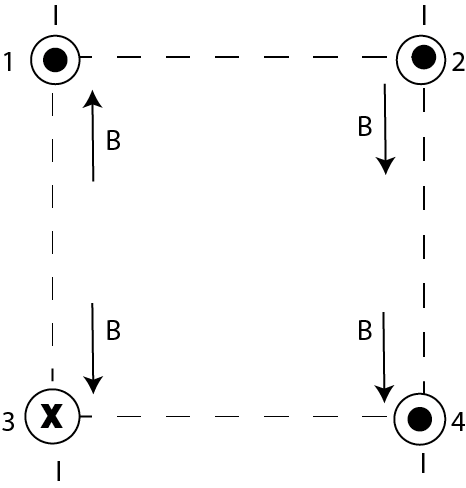
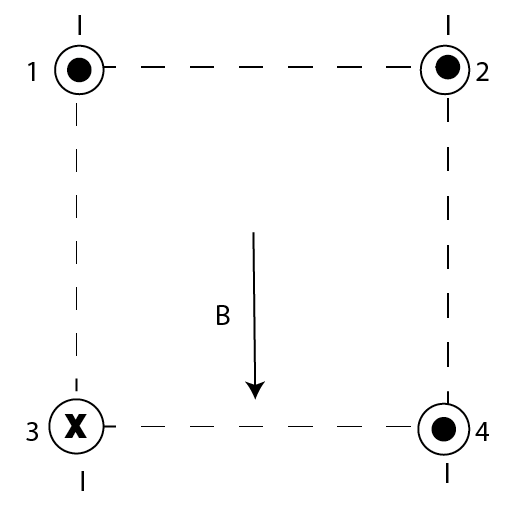
For the loop to counter this magnetic field, we need it to be inside. For the field to point inside, the current must flow counterclockwise and because of the equal distances, $R$ the field in the center of the loop is going to be zero.
$$
begin{aligned}
r = frac{mv}{lvert q rvert B} tag{1}
end{aligned}
$$
where $m$ is the mass of the object, $v$ is its velocity, $q$ is the charge and $B$ is the magnetic field.
**GIVEN**
Radius: $r = 220;text{m}$
Velocity: $1.1times 10^{8};text{m/s}$
Charge: $q = 1.6 times 10^{-19};text{C}$
Mass of electron: $m = 9.11times 10^{-31};text{kg}$
$$
begin{aligned}
B &= frac{mv}{lvert q rvert r} \ &= frac{(9.11times 10^{-31};text{kg})(1.1times 10^{8};text{m/s})}{(1.6 times 10^{-19};text{C})(220;text{m})} \ &= boxed{2.85times 10^{-6};text{T}}
end{aligned}
$$
$B = dfrac{mu_0 I}{2 pi r}$
where $mu_0 = 4 pi times 10^{-7}: T.m.A^{-1}$
So, $B = dfrac{^2 cancel{4 pi} times 10^{-7} times I}{cancel{2 pi} r} = dfrac{2 times 10^{-7} times I}{r}$
Magnetic field produced by lightning bolt carrying current of $225:kA = 225 times 10^3:A$ at a distance of $35:m$ is given by
$B = dfrac{2 times 10^{-7} times 225 times 10^3}{35} = 12.86 times 10^{-4}:T$
are in the same direction, hence the magnitude of the force will be
maximum. For $v_{2}$and $v_{4}$ the direction of magnetic force
and electric force are in perpendicular direction. Hence the magnitude
of the force will be same. For $v_{3}$ the direction of magnetic
force and electric force are in opposite direction, hence the magnitude
will be minimum for $v_{3}$. Hence in increasing order of force we
have
$$
v_{3}<v_{2}=v_{4}<v_{1}
$$
opposite direction the total force can be zero for $v_{3}$.
Also, commonly mistaken is that geographic and magnetic fields are the same, but the north geographic pole of Earth is actually near the south pole of Earth’s magnetic field.
The average strength of the Earth’s magnetic field is around $5.0 times 10^{-5} mathrm{~T}$.
The continental drift (moving of the continents) and seafloor patterns have been observed, which are direct proof of Earth’s magnetic field, as the rocks are having specific magnetization when they were cooled in seawater. Lava from vulcanos would cool fast and “capture” Earth’s magnetization at the moment.
This is proof also that Earth’s magnetic field is changing constantly and at one point south and east magnetic poles are going to change, even small “ripples” in change have already been observed in Africa.
The last time this happened between 980,000 years and 780,000 years ago. When this happens again it is not gonna be dangerous, as the field is not so strong on the Earth’s surface.
Due to this change, there are still research and nothing is fully predicted. The North and south pole are going to change, so animals that are using magnetic fields to navigate could be confused at the beginning and our compass needle is going to point toward the south geographical pole from now on.
During the reverse, there is a small moment when there will be no magnetic field, but this moment is short, so hopefully will not cause any damage to our everyday life.
* – both of the fields are produced by the charges. Electric field by the static charge, but magnetic fields only by the charges in motion
* – the electric field can be a monopole (only one charge, positive or negative), while the magnetic field always comes in a dipole. Magnetic monopoles do not exist.
* – we usually note magnetic field with $B$ and the unit is Tesla (T), while we note electric field with E and units is $frac{V}{m}$
* – the electric field has a start and end. Positive charges are sources of electric fields. The electric field starts in a positive charge and ends in a negative charge. Magnetic fields are infinite loops, they do not start or end in any of the poles.
* – both fields are radially dependent, while with electric we have inversely proportionality to the square of the radius, with the magnetic field it is usually only radius (to the first power).
* – electric field makes a charged particle move linearly, while magnetic field makes a charged particle moving in a circular motion.
$B = dfrac{mu_0 I}{2 pi r}$ where $mu_0 = 4 pi times 10^{-7}:T.m.A^{-1}$
$B = dfrac{^2 cancel{4 pi} times 10^{-7} times I} {cancel{2 pi} r} = dfrac{2 times 10^{-7} times I}{r}$
The current required to produce a magnetic field of $1.0 times 10^{-15}:T$ at a radial distance of $5.0:cm = 0.05:m$ is given by
$I = dfrac{B r}{2 times 10^{-7}} = dfrac{Br}{2} times 10^7$; Substituting the values,
$I = dfrac{1.0 times 10^{-15} times 0.05}{2} times 10^7 = 0.025 times 10^{-8} = 2.5 times 10^{-10}:A$
$B = dfrac{mu_0 I}{2 pi r}$; where $mu_0 = 4 pi times 10^{-7} : T.m.A^{-1}$.
$B = dfrac{^2cancel{4 pi} times 10^{-7} times I}{cancel{2 pi} r} = dfrac{2 times 10^{-7} times I}{r}$
Given data are
$I = 5.0 times 10^{-8}:A$ and $r = 7.5:cm = 0.075:m$
So, $B = dfrac{2 times 10^{-7} times 5.0 times 10^{-8}}{0.075} =133 times 10^{-15} = 1.3 times 10^{-13}:T$
$B = dfrac{mu_0 I}{2 pi r}$; where $mu_0 = 4 pi times 10^{-7} : T.m.A^{-1}$.
$B = dfrac{^2cancel{4 pi} times 10^{-7} times I}{cancel{2 pi} r} = dfrac{2 times 10^{-7} times I}{r}$
The radial distance of a point at which $3.1 times 10^{-8}:A$ current produces magnetic field of $2.8 times 10^{-14}:T$ is given by
$r = dfrac{2 times 10^{-7} times I}{B} = dfrac{2 times 10^{-7} times 3.1 times 10^{-8}}{2.8 times 10^{-14}} = dfrac{2 times 3.1}{2.8} times 10^{-1} =0.22:m$
$$
r = 22:cm
$$

