
All Solutions
Page 336: Assessment
To understand how the gravitational force between the human is extremely small. Let the two persons have masses $70 mathrm{~kg}$ and $50 mathrm{~kg}$ and the separation between them $0.5 mathrm{~m}$. As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{2} }{ r^{2} } \
&= 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} ~ dfrac{ 70 mathrm{~kg} times 50 mathrm{~kg} }{ left( 0.5 mathrm{~m} right)^{2} } \
&= 9.338 times 10^{-7} mathrm{~N}
end{align*}
$$
As we see from the previous calculations, the gravitational force between the human is extremely small in a range of $9.338 times 10^{-7} mathrm{~N}$. So, we can neglect it.
Solve for the first case (before the separation halved):
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F_{1} &= G ~ dfrac{ m_{1} ~ m_{2} }{ r_{1}^{2} } \
end{align*}
$$
Solve for the second case (after the separation halved):
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F_{2} &= G ~ dfrac{ m_{1} ~ m_{2} }{ r_{2}^{2} } \
&= G ~ dfrac{ m_{1} ~ m_{2} }{ left( dfrac{1}{2} ~ r_{1} right)^{2} } \
&= G ~ dfrac{ m_{1} ~ m_{2} }{ dfrac{1}{4} r_{1}^{2} } \
&=4 ~ G ~ dfrac{ m_{1} ~ m_{2} }{ r_{1}^{2} } \
&= 4 ~ F_{1}
end{align*}
$$
So, if the separation between the two masses is halved, then the gravitational force between them will increase by the factor of 4 (quadruple).
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{2} }{ r^{2} } \
end{align*}
$$
As we see the gravitational force depends on the product of two objects’ masses due to Newton’s law of universal gravitation which is practical law (comes from observations).
Solve for $m_{1} = 0$:
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{2} }{ r^{2} } \
&= G ~ dfrac{ 0 mathrm{~kg} ~ m_{2} }{ r^{2} } \
&= 0 mathrm{~N}
end{align*}
$$
So, if the mass of one object goes to zero, then the gravitational force between the two objects equals zero.
Solve for first case (before the mass $m_{1}$ doubled):
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{2} }{ r^{2} } \
end{align*}
$$
Solve for second case (after the mass $m_{1}$ doubled):
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F’ &= G ~ dfrac{ m_{1}’ ~ m_{2} }{ r^{2} } \
&= G ~ dfrac{2 m_{1} ~ m_{2} }{ r^{2} } \
&= 2 G ~ dfrac{ m_{1} ~ m_{2} }{ r^{2} } \
&= 2 F
end{align*}
$$
So, if the mass $m_{1}$ doubled, then the gravitational force between the two objects doubles.
If the mass of one object goes to zero, then the gravitational force between the two objects equals zero.
If the mass $m_{1}$ doubled, then the gravitational force between the two objects doubles.
textbf{Concept:}
$$
Employ the Newton’s law of universal gravitation to find the magnitude of force between each pair of objects. Later rank the calculated values to get the comparison.
$$
textbf{Solution:}
$$
Finding the gravitational forces we get
$$
F_A=Gfrac{m_{1,A}m_{2,A}}{r^2_A}=Gfrac{mm}{r^2}=Gfrac{m^2}{r^2}
$$
$$
F_B=Gfrac{m_{1,B}m_{2,B}}{r^2_B}=Gfrac{m(2m)}{(2r^2)}=frac{1}{2}Gfrac{m^2}{r^2}
$$
$$
F_C=Gfrac{m_{1,C}m_{2,C}}{r^2_C}=Gfrac{(2m)(3m)}{(2r^2)}=frac{3}{2}Gfrac{m^2}{r^2}
$$
$$
F_D=Gfrac{m_{1,D}m_{2,D}}{r^2_D}=Gfrac{(4m)(5m)}{(3r^2)}=frac{30}{9}Gfrac{m^2}{r^2}
$$
Now make comparison to arrive at result $boxed{ bf color{#4257b2}B<A<C<D}$
B<A<C<D
$$
The mass of the peach is $m_{1} = 0.16 mathrm{~kg}$.
$textbf{Required: }$
(a) Finding the magnitude gravitational force, if the separation between them is $0.25 mathrm{~m}$.
(b) Finding the magnitude gravitational force, if the separation between them is $0.5 mathrm{~m}$.
Solve for the two peachs are identical $m_{1} = m_{2}$:
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{2} }{ r^{2} } \
&= 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} ~ dfrac{left( 0.16 mathrm{~kg} right)^{2} }{ left( 0.25 mathrm{~m} right)^{2} } \
&= 2.732 times 10^{-11} mathrm{~N}
end{align*}
$$
So, the magnitude of the gravitational force is $2.732 times 10^{-11} mathrm{~N}$.
Solve for the two peachs are identical $m_{1} = m_{2}$:
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{2} }{ r^{2} } \
&= 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} ~ dfrac{left( 0.16 mathrm{~kg} right)^{2} }{ left( 0.5 mathrm{~m} right)^{2} } \
&= 6.83 times 10^{-12} mathrm{~N}
end{align*}
$$
So, the magnitude of the gravitational force is $6.83 times 10^{-12} mathrm{~N}$.
(b) The magnitude of the gravitational force is $2.732 times 10^{-11} mathrm{~N}$.
The mass of the first bowling ball is $m_{1} = 6.8 mathrm{~kg}$. The mass of the second bowling ball is $m_{2} = 7.1 mathrm{~kg}$. The separation between the two balls is $r = 0.75 mathrm{~m}$.
$textbf{Required: }$
Finding the gravitational force between them.
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{2} }{ r^{2} } \
&= 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} ~ dfrac{ 6.8 mathrm{~kg} times 7.1 mathrm{~kg} }{ left( 0.75 mathrm{~m} right)^{2} } \
&= 5.725 times 10^{-9} mathrm{~N}
end{align*}
$$
So, the magnitude of the gravitational force between the two balls is $5.725 times 10^{-9} mathrm{~N}$.
The mass of the apple is $m_{1} = 0.11 mathrm{~kg}$. The mass of the orange is $m_{2} = 0.24 mathrm{~kg}$. The separation between the apple and the orange is $r = 0.85 mathrm{~m}$.
$textbf{Required: }$
(a) Finding the gravitational force that the orange exerted on the apple.
(b) Finding the gravitational force that exerted by the apple on the orange.
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{2} }{ r^{2} } \
&= 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} ~ dfrac{ 0.11 mathrm{~kg} times 0.24 mathrm{~kg} }{ left( 0.85 mathrm{~m} right)^{2} } \
&= 2.437 times 10^{-12} mathrm{~N}
end{align*}
$$
So, the magnitude of the gravitational force by the orange on the apple is $2.437 times 10^{-12} mathrm{~N}$.
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{2} }{ r^{2} } \
&= 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} ~ dfrac{ 0.24 mathrm{~kg} times 0.11 mathrm{~kg} }{ left( 0.85 mathrm{~m} right)^{2} } \
&= 2.437 times 10^{-12} mathrm{~N}
end{align*}
$$
So, the magnitude of the gravitational force on the orange by the apple is $2.437 times 10^{-12} mathrm{~N}$. As we see the two gravitational forces are equal in magnitude and opposite in direction.
(b) The magnitude of the gravitational force on the orange by the apple is $2.437 times 10^{-12} mathrm{~N}$. As we see the two gravitational forces are equal in magnitude and opposite in direction.
textbf{Concept:}
$$
By applying the Newton’s law of universal gravitation we can relate the attractive forces from Earth and the Moon. Assume the force due to Earth is equal to twice the force caused by the Moon when the spaceship is at a separation r from the centre of Earth. Assume $R=3.84 times 10^8 m$, and the distance between the centers of Earth and the Moon. Then solve the expression for the distance be $r$.
$$
textbf{Solution:}
$$
Assume $F_E=2F_M$ and use Newton’s law of gravity to solve for $r$
$$
cancel{G}frac{cancel{m_s} m_E}{r^2}=2times cancel{G}frac{cancel{m_s} m_M}{(R-r)^2}
$$
$$
m_E(R-r)^2=2m_Mr^2Rightarrow R-r=sqrt{2m_M/m_Er}Rightarrow =sqrt{2m_M/m_Er}+r
$$
$$
r=frac{R}{1+sqrt{2m_M/m_Er}}=frac{3.84times 10^8m}{1+sqrt{2(7.35times 10^{22})bigg/(5.97times 10^{24 kg})}}
$$
$$
=boxed{color{#4257b2} bf 3.32times 10^8;m}
$$
Sum up the gravitational force on the Moon caused by other two masses by applying Newton’s law of gravity. The
forces are attractive and to be added as vectors. Assume the force toward the left (toward the Sun) to be positive and the force toward Earth to be negative.
textbf{Solution:}
Sum the force\
$$vec{F}_M=Gfrac{M_S M_M}{r^2_{S-M}}-Gfrac{M_E M_M}{r^2_{E-M}}=GM_Mbigg[frac{M_S}{r^2_{S-M}}-frac{M_E}{r^2_{E-M}}bigg]$$
$$vec{F}_M=(6.67times 10^{-11}N.m^2/kg^2)(7.35times 10^{22}kg)bigg[frac{2.00times 10^{30}}{(1.5times 10^{11}-3.84times 10^8 m)^2}-frac{5.97times 10^{24}kg}{(3.84 times 10^{8}m)^2}bigg]$$
$$boxed{ bf color{blue}vec{F}_M=2.4times 10^{20}N mbox{ Towards the sun}}$$
The mass of each object is $m = 6.75 mathrm{~kg}$. The separation between two objects (length of the triangle) is $r = 0.25 mathrm{~m}$.
$textbf{Required: }$
Finding the magnitude total gravitational force.
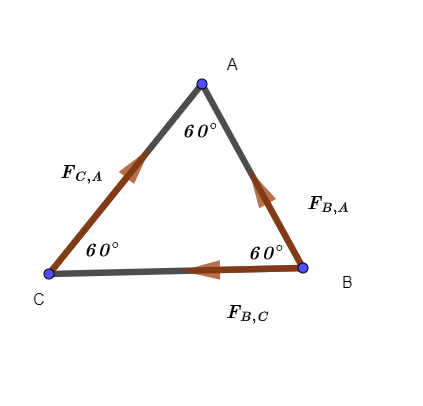
Solve for the two peachs are identical $m_{1} = m_{2}$:
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{2} }{ r^{2} } \
&= G ~ dfrac{ m^{2} }{ r^{2} } ~ cos left( theta right) \
end{align*}
$$
So, the magnitude of the total force exerted on each mass is given by
$$
begin{align*}
F &= 2 ~ G ~ dfrac{ m^{2} }{ r^{2} } ~ cos left( theta right) \
&= 2 times 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} ~ dfrac{left( 6.75 mathrm{~kg} right)^{2} }{ left( 1.25 mathrm{~m} right)^{2} } ~ cos left( 30^{circ} right) \
&= 3.369 times 10^{-9} mathrm{~N}
end{align*}
$$
So, the magnitude total gravitational force is $3.369 times 10^{-9} mathrm{~N}$.
textbf{Concept:}
$$
Sum up the forces of gravity using the component method for vector addition. The use Newton’s law of gravity and the geometry of the problem to find the value of the forces. Let $m_1 = 1.0 kg$, $m_2 = 2.0 kg$, $m_3= 3.0 kg$, and $m_4 = 4.0 kg$.
$$
textbf{Solution:}
$$
Compute the x component of the force on $m_2$. The cos of the angle is the adjacent side of the triangle $r_{12}$ divided by the hypotenuse $r_{24}$
$$
F_x=Gfrac{m_1m_2}{r^2_{12}}+Gfrac{m_2m_4}{r^2_{24}} cos phi
$$
$$
F_x=Gfrac{m_1m_2}{r^2_{12}}+Gfrac{m_2m_4}{r^2_{24}} bigg[frac{r_{12}}{r_{24}}bigg]=gm_2bigg[frac{m_1}{r^2_{12}}+frac{m_4r_{12}}{r^3_{24}}bigg]
$$
$$
F_x=(6.67times 10^{-11}N.m^2/kg^2)(2.0kg)Bigg[frac{1.0kg}{(0.20m)^2}+frac{(4.0kg)(0.20m)}{[(0.20)^2+(0.10)^2]^{3/2}}bigg]
$$
$$
F_x=1.3times 10^{-8}N
$$
Now find the y-component of the force
$$
F_y=Gfrac{m_2m_3}{r^2_{23}}+Gfrac{m_2m_4}{r^2_{24}} sin phi
$$
$$
F_y=Gfrac{m_2m_3}{r^2_{23}}+Gfrac{m_2m_4}{r^2_{24}} bigg[frac{r_{14}}{r_{24}}bigg]=Gm_2bigg[frac{m_3}{r^2_{23}}+frac{m_4r_{14}}{r^3_{24}}bigg]
$$
$$
F_y=(6.67times 10^{-11}N.m^2/kg^2)(2.0kg)Bigg[frac{3.0kg}{(0.10m)^2}+frac{(4.0kg)(0.10m)}{[(0.20)^2+(0.10)^2]^{3/2}}bigg]
$$
$$
F_y=4.5times 10^{-8}N
$$
Now sum the two components to get the final vector force $vec{F}$
$$
vec{F}=sqrt{F^2_x+F^2_y}=sqrt((1.3times 10^{-8}N)^2+(4.5times 10^{-8}N)^2)
$$
$$
boxed{ bf color{#4257b2}vec{F}=4.7times 10^{-8};N}
$$
vec{F}=4.7times 10^{-8};N
$$
Solve for the first object that is placed in $A$ point:
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{2} }{ r^{2} } \
end{align*}
$$
According to the superposition principle, the total gravitational force that acts on the object that is placed in $A$ point is given by
$$
begin{align*}
F_{A} &= – F_{A,B} – F_{A,C} \
&= -G ~ dfrac{ m_{A} ~ m_{B} }{ r_{A,B}^{2} } -G ~ dfrac{ m_{A} ~ m_{C} }{ r_{A,C}^{2} } \
&= -G left( dfrac{ m_{A} ~ m_{B} }{ r_{A,B}^{2} } – dfrac{ m_{A} ~ m_{C} }{ r_{A,C}^{2} } right) \
&= -G left( dfrac{ M ~ 2M }{ r^{2} } – dfrac{ M ~ 3M }{ left( 2 r right)^{2} } right) \
&= G ~ dfrac{ M^{2} }{ r^{2} } ~ left( -2 – dfrac{3}{ left( 2 right)^{2} } right) \
&= -G ~ dfrac{ M^{2} }{ r^{2} } ~ dfrac{11}{4} \
&= -G ~ dfrac{ 11 ~ M^{2} }{ 4 ~ r^{2} }
end{align*}
$$
So, the total gravitational force that acts on the object that is placed in $A$ point is $G ~ dfrac{ -11 ~ M^{2} }{ 4 ~ r^{2} }$.
Solve for the first object that is placed in $B$ point:
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{2} }{ r^{2} } \
end{align*}
$$
According to the superposition principle, the total gravitational force that acts on the object that is placed in $B$ point is given by
$$
begin{align*}
F_{B} &= F_{B,A} + F_{B,C} \
&= G ~ dfrac{ m_{A} ~ m_{B} }{ r_{A,B}^{2} } -G ~ dfrac{ m_{A} ~ m_{C} }{ r_{B,C}^{2} } \
&= G left( dfrac{ m_{A} ~ m_{B} }{ r_{A,B}^{2} } – dfrac{ m_{B} ~ m_{C} }{ r_{B,C}^{2} } right) \
&= G left( dfrac{M ~ 2M }{ r^{2} } – dfrac{ 2M ~ 3 M }{ r^{2} } right) \
&= G ~ dfrac{ M^{2} }{ r^{2} } ~ left( 2 -6 right) \
&= G ~ dfrac{ – 4 M^{2} }{ r^{2} }
end{align*}
$$
So, the total gravitational force that acts on the object that is placed in $B$ point is $G ~ dfrac{ – 4M^{2} }{ r^{2} }$.
Solve for the first object that is placed in $C$ point:
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{2} }{ r^{2} } \
end{align*}
$$
According to the superposition principle, the total gravitational force that acts on the object that is placed in $C$ point is given by
$$
begin{align*}
F_{C} &= F_{C,A} + F_{C,B} \
&= G ~ dfrac{ m_{A} ~ m_{C} }{ r_{C,A}^{2} } +G ~ dfrac{ m_{B} ~ m_{C} }{ r_{B,C}^{2} } \
&= G left( dfrac{ m_{A} ~ m_{C} }{ r_{A,C}^{2} } + dfrac{ m_{B} ~ m_{C} }{ r_{B,C}^{2} } right) \
&= G left( dfrac{ M ~ 3M }{ left( 2 r right)^{2} } + dfrac{3 M ~2 M }{ r^{2} } right) \
&= G ~ dfrac{ M^{2} }{ r^{2} } ~ left( dfrac{3}{ left( 2 right)^{2} } +6 right) \
&= G ~ dfrac{ M^{2} }{ r^{2} } ~ dfrac{27}{4} \
&= G ~ dfrac{ 27 ~ M^{2} }{ 4 ~ r^{2} }
end{align*}
$$
So, the total gravitational force that acts on the object that is placed in $C$ point is $G ~ dfrac{ 27 ~ M^{2} }{ 4 ~ r^{2} }$.
Since $G ~ dfrac{ 27 ~ M^{2} }{ 4 ~ r^{2} } > G ~ dfrac{ – 4M^{2} }{ r^{2} } > G ~ dfrac{ -11 ~ M^{2} }{ 4 ~ r^{2} }$, Then $F_{C} > F_{B} > F_{A}$.
Solve for the first Case:
According to Newton’s second law, the force due to the gravity (Weight) is given by
$$
begin{align*}
F &= W \
&= m_{1} ~ a \
end{align*}
$$
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{2} }{ r^{2} } \
&= m_{1} ~ a \
end{align*}
$$
Rearrange and solve for the acceleration due to the gravitational force:
$$
begin{align*}
a &= G ~ dfrac{ m_{2} }{r^{2} } \
end{align*}
$$
Solve for the second Case after the mass of the planet doubled:
According to Newton’s second law, the force due to the gravity (Weight) is given by
$$
begin{align*}
F &= W \
&= m_{1} ~ a \
end{align*}
$$
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{2}’ }{ r’^{2} } \
&= m_{1} ~ a \
end{align*}
$$
Rearrange and solve for the acceleration due to the gravitational force:
$$
begin{align*}
a’ &= G ~ dfrac{ m_{2}’ }{r^{2} } \
&= G ~ dfrac{ 2m_{2} }{ r^{2} } \
&= 2 ~ G ~ dfrac{ m_{2} }{ r^{2} } \
&= 2 ~ a
end{align*}
$$
So, if both the mass of the planet were doubled, then the acceleration due to gravity at its surface will double, too.
Solve for the first Case before the radius of the planet doubled:
According to Newton’s second law, the force due to the gravity (Weight) is given by
$$
begin{align*}
F &= W \
&= m_{1} ~ a \
end{align*}
$$
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{2} }{ r^{2} } \
&= m_{1} ~ a \
end{align*}
$$
Rearrange and solve for the acceleration due to the gravitational force:
$$
begin{align*}
a &= G ~ dfrac{ m_{2} }{r^{2} } \
end{align*}
$$
Solve for the second Case after the radius of the planet doubled:
According to Newton’s second law, the force due to the gravity (Weight) is given by
$$
begin{align*}
F &= W \
&= m_{1} ~ a \
end{align*}
$$
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{2}’ }{ r’^{2} } \
&= m_{1} ~ a \
end{align*}
$$
Rearrange and solve for the acceleration due to the gravitational force:
$$
begin{align*}
a’ &= G ~ dfrac{ m_{2} }{r’^{2} } \
&= G ~ dfrac{ m_{2} }{ left( 2 r right)^{2} } \
&= dfrac{1}{4} ~ G ~ dfrac{ m_{2} }{ r^{2} } \
&= dfrac{1}{4} ~ a
end{align*}
$$
So, if both the radius of the planet were doubled, then the acceleration due to gravity at its surface decreases by the factor of $4$.
textbf{Concept:}
$$
Applying the Newton’s law of universal gravitation to calculate the relative values of the accelerations experienced by each object. In a previous problem we found the forces: $F_A=frac{11}{4}GM^2/L^2$, $F_B=4GM^2/L^2$, $F_C=frac{27}{4}GM^2/L^2$
$$
textbf{Solution:}
$$
Calculate the acceleration of object A
$$
A_A=frac{F_A}{m_A}=frac{11}{4}frac{GM^2/L^2}{M}=frac{11}{4}frac{GM}{L^2}=frac{33}{12}frac{GM}{L^2}
$$
In a similar way calculate the acceleration of object B
$$
A_B=frac{F_B}{m_B}=frac{4}{2}frac{GM^2/L^2}{2M}=2frac{GM}{L^2}=frac{24}{12}frac{GM}{L^2}
$$
Calculate the acceleration of object C
$$
A_C=frac{F_C}{m_C}=frac{27}{4}frac{GM^2/L^2}{3M}=frac{27}{12}frac{GM}{L^2}
$$
By comparison we found that $boxed{ bf color{#4257b2}B<C<A}$
boxed{ bf color{#4257b2}B<C<A}
$$
The mass of Titan is $m_{t} = 1.35 times 10^{23} mathrm{~kg}$.The radius of Titan is $R_{t} = 2.57 times 10^{6} mathrm{~m}$.
$textbf{Required: }$
Finding the acceleration due to the gravity at the surface of Titan.
According to Newton’s second law, the force due to the gravity (Weight) is given by
$$
begin{align*}
F &= W \
&= m_{1} ~ a \
end{align*}
$$
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{t} }{ r^{2} } \
&= m_{1} ~ a \
&= G ~ dfrac{ m_{1} ~ m_{t} }{ R_{m}^{2} } \
end{align*}
$$
Rearrange and solve for the acceleration due to the gravity at the surface of Titan:
$$
begin{align*}
a &= G ~ dfrac{ m_{t} }{ R_{t}^{2} } \
&= 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} ~ dfrac{ 1.35 times 10^{23} mathrm{~kg} }{ left( 2.57 times 10^{6} mathrm{~m} right)^{2} } \
&= 1.363 mathrm{~m/s^{2}}
end{align*}
$$
So, the acceleration due to the gravity at the surface of Titan is $1.363 mathrm{~m/s^{2}}$.
The mass of Mercury is $m_{m} = 3.285 times 10^{23} mathrm{~kg}$.The radius of Titan is $R_{t} = 2.4397 times 10^{6} mathrm{~m}$. The mass of Venus is $m_{v} = 4.867 times 10^{24} mathrm{~kg}$.The radius of Venus is $R_{v} = 6.052 times 10^{6} mathrm{~m}$.
$textbf{Required: }$
(a) Finding the acceleration due to the gravity at the surface of Mercury.
(b) Finding the acceleration due to the gravity at the surface of Venus.
According to Newton’s second law, the force due to the gravity (Weight) is given by
$$
begin{align*}
F &= W \
&= m_{1} ~ a \
end{align*}
$$
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{m} }{ r^{2} } \
&= m_{1} ~ a \
&= G ~ dfrac{ m_{1} ~ m_{m} }{ R_{m}^{2} } \
end{align*}
$$
Rearrange and solve for the acceleration at the surface of Mercury:
$$
begin{align*}
a &= G ~ dfrac{ m_{m} }{ R_{m}^{2} } \
&= 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} ~ dfrac{ 3.285 times 10^{23} mathrm{~kg} }{ left( 2.4397 times 10^{6} mathrm{~m} right)^{2} } \
&= 3.681 mathrm{~m/s^{2}}
end{align*}
$$
So, the acceleration due to the gravity at the surface of Mercury is $3.681 mathrm{~m/s^{2}}$.
According to Newton’s second law, the force due to the gravity (Weight) is given by
$$
begin{align*}
F &= W \
&= m_{1} ~ a \
end{align*}
$$
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{v} }{ r^{2} } \
&= m_{1} ~ a \
&= G ~ dfrac{ m_{1} ~ m_{v} }{ R_{m}^{2} } \
end{align*}
$$
Rearrange and solve for the acceleration at the surface of Venus:
$$
begin{align*}
a &= G ~ dfrac{ m_{v} }{ R_{v}^{2} } \
&= 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} ~ dfrac{ 4.867 times 10^{24} mathrm{~kg} }{ left( 6.052 times 10^{6} mathrm{~m} right)^{2} } \
&= 8.863 mathrm{~m/s^{2}}
end{align*}
$$
So, the acceleration due to the gravity at the surface of Venus is $8.863 mathrm{~m/s^{2}}$.
(b) The acceleration due to the gravity at the surface of Venus is $8.863 mathrm{~m/s^{2}}$.
The mass of Earth is $M_{E} = 5.96 times 10^{24} mathrm{~kg}$. The radius of Earth is $R_{E} = 6.37 times 10^{6} mathrm{~m}$. The accerlation due to Earth at certain height on the satellite is $a = dfrac{ g}{4}$.
$textbf{Required: }$
Finding the height of the satellite.
According to Newton’s second law, the force due to the gravity (Weight) is given by
$$
begin{align*}
F &= W \
&= m_{1} ~ a \
end{align*}
$$
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{E} }{ r^{2} } \
&= m_{1} ~ a \
&= G ~ dfrac{ m_{1} ~ m_{E} }{ r^{2} } \
end{align*}
$$
Rearrange and solve for the acceleration due to the gravity at the altitude of the satellite orbit:
$$
begin{align*}
a &= G ~ dfrac{ m_{E} }{ r^{2} } \
&= dfrac{ g}{4} \
end{align*}
$$
Rearrange and solve for the acceleration due to the gravity at the altitude of the satellite orbit:
$$
begin{align*}
a &= G ~ dfrac{ m_{E} }{r^{2} } \
&= G ~ dfrac{ m_{E} }{ left( R_{E} + h right)^{2} } \
&= dfrac{ g}{4} \
end{align*}
$$
Rearrange and solve for the height of the satellite above the Earth’s surface:
$$
begin{align*}
left( R_{E} + h right)^{2} &= G ~ dfrac{ m_{E} }{ dfrac{ g}{4} } \
&=4 G ~ dfrac{ m_{E} }{ g } \
h &= sqrt{ 4 G ~ dfrac{ m_{E} }{ g } } – R_{E} \
&= sqrt{ 4 times 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} times dfrac{ 5.96 times 10^{24} mathrm{~kg} }{ 9.8 mathrm{~m/s^{2}} } } – 6.37 times 10^{6} mathrm{~m} \
&= 6.368 times 10^{6} mathrm{~m}
end{align*}
$$
So, the height of the satellite is $6.368 times 10^{6} mathrm{~m}$.
The mass of Earth is $M_{E} = 5.96 times 10^{24} mathrm{~kg}$. The radius of Earth is $R_{E} = 6.37 times 10^{6} mathrm{~m}$. The separation between Earth and the Moon is $r = 3.84 times 10^{8} mathrm{~m}$.
$textbf{Required: }$
Finding the acceleration due to the Earth’s gravity at the given distance.
According to Newton’s second law, the force due to the gravity (Weight) is given by
$$
begin{align*}
F &= W \
&= m_{1} ~ a \
end{align*}
$$
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{E} }{ r^{2} } \
&= m_{1} ~ a \
&= G ~ dfrac{ m_{1} ~ m_{E} }{ R_{m}^{2} } \
end{align*}
$$
Rearrange and solve for the acceleration due to the Earth’s gravity at the given distance.:
$$
begin{align*}
a &= G ~ dfrac{ m_{E} }{ r^{2} } \
&= 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} ~ dfrac{ 5.96 times 10^{24} mathrm{~kg} }{ left( 3.84 times 10^{8} mathrm{~m} right)^{2} } \
&= 2.696 times 10^{-3} mathrm{~m/s^{2}}
end{align*}
$$
So, the acceleration due to the Earth’s gravity at the given distance is $2.696 times 10^{-3} mathrm{~m/s^{2}}$.
The mass of the satellite is $m_{1} = 480 mathrm{~kg}$. The mass of Earth is $M_{E} = 5.96 times 10^{24} mathrm{~kg}$. The separation between the center of Earth and the satellite is $r = 3.5 times 10^{7} mathrm{~m}$.
$textbf{Required: }$
Finding the gravitational force by Earth than exerted on the satellite.
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ M_{E} }{ r^{2} } \
&= 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} ~ dfrac{ 480 mathrm{~kg} times 5.96 times 10^{24} mathrm{~kg} }{ left(3.5 times 10^{7} mathrm{~m} right)^{2} } \
&= 156.029 mathrm{~N}
end{align*}
$$
So, the magnitude of the gravitational force by Earth on the satellite is $156.029 mathrm{~N}$.
The mass of Earth is $M_{E} = 5.96 times 10^{24} mathrm{~kg}$. The mass of the object is $m_{1} = 12 mathrm{~kg}$. The weight of the object is $W = F = 15 mathrm{~N}$.
$textbf{Required: }$
Finding the distance from the center of Earth and the object.
According to Newton’s second law, the force due to the gravity (Weight) is given by
$$
begin{align*}
F &= W \
&= m_{1} ~ a \
end{align*}
$$
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ M_{E} }{ r^{2} }
end{align*}
$$
Rearrange and solve for the distance between the two bowling balls:
$$
begin{align*}
r &= sqrt{ G ~ dfrac{ m_{1} ~ M_{E} }{ F} } \
&= sqrt{ G ~ dfrac{ m_{1} ~ M_{2} }{ W} } \
&= sqrt{ 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} ~ dfrac{ 12 mathrm{~kg} times 5.96 times 10^{24} mathrm{~kg} }{ 15 mathrm{~N} } } \
&= 1.783 times 10^{7} mathrm{~m}
end{align*}
$$
So, the distance from the center of Earth and the object is $1.783 times 10^{7} mathrm{~m}$.
textbf{Concept:}
$$
By applying the Newton’s universal law of gravitation we find the attractive forces from Earth and the Moon. Let the force applied to Earth equal to the force due to the Moon when the spaceship is at a separation $r$ from the center of Earth. Let $R=3.84times 10^8m$, which is the distance between the centers of Earth and the Moon. Lastly solve the expression for the distance $r$.
$$
textbf{Solution:}
$$
Use the assumption that $F_E=F_M$ and use law of gravity to solve for $r$ we get
$$
cancel{G}frac{cancel{m}_SM_E}{r^2}=cancel{G}frac{cancel{m}_SM_M}{(R-r)^2}
$$
$$
m_S(R-r)^2=m_M r^2Rightarrow R-r =sqrt{2m_M/2_Er} Rightarrow R = sqrt{2m_M/m_Er}+r
$$
$$
r=frac{R}{1+sqrt{m_M/m_E}}=frac{3.84 times 10^8m}{1+sqrt{(7.35 times 10^{22}kg)/(5.97 times 10^{24}kg)}}=boxed{ bf color{#4257b2}3.46 times 10^8m}
$$
r=3.46 times 10^8m
$$
The acceleration of gravity at the surface of Mars is $a_{M} = 0.38 ~ g$. The radius of Mars is $r_{M} = 0.53 ~ r_{E}$.
$textbf{Required: }$
Finding the mass of Mars in terms of mass of Earth.
Solve for the Mars case:
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F_{M} &= G ~ dfrac{ m_{1} ~ m_{M} }{ r_{M}^{2} } \
end{align*}
$$
Rearrange and solve for the mass of the Moon:
$$
begin{align*}
m_{M} &= dfrac{ F_{M} ~ r_{M}^{2} }{ m_{1} ~ G} \
end{align*}
$$
Solve for the Earth’s case:
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F_{E} &= G ~ dfrac{ m_{1} ~ m_{E} }{ r_{E}^{2} } \
end{align*}
$$
Rearrange and solve for the mass of the Moon:
$$
begin{align*}
m_{E} &= dfrac{ F_{E} ~ r_{E}^{2} }{ m_{1} ~ G} \
end{align*}
$$
divide both equations together, then we get
$$
begin{align*}
dfrac{ m_{M} }{ m_{E} } &= dfrac{ dfrac{ F_{M} ~ r_{M}^{2} }{ m_{1} ~ G} }{ dfrac{ F_{E} ~ r_{E}^{2} }{ m_{1} ~ G} } \
&= dfrac{ dfrac{ m ~ a_{M} ~ r_{M}^{2} }{ m_{1} ~ G} }{ dfrac{ m ~ a_{E} ~ r_{E}^{2} }{ m_{1} ~ G} } \
&= dfrac{ a_{M} ~ r_{M}^{2} }{a_{E} ~ r_{E}^{2} } \
&= dfrac{ 0.38 ~ g times left( 0.53 ~ r_{E} right)^{2} }{ g times r_{E}^{2} } \
&= 0.38 ~ left( 0.53 right)^{2} \
&= 0.107
end{align*}
$$
So, the mass of the Moon in terms of the mass of Earth is $0.107 M_{E}$.
According to Newton’s second law:
$$
begin{align*}
f_{cp} &=m ~ a_{cp} \
&= f_{s}
end{align*}
$$
As Newton’s second law for circular motion, the centripetal force is given by the mass time the centripetal acceleration:
$$
begin{align*}
f_{cp} &= m ~ a_{cp} \
&= m ~ dfrac{ v^{2} }{ r} \
end{align*}
$$
So, the spin cycle of the basket of radius $r$ inside the washing machine exerts a force $F$ on the clothes of mass $m$ that moves with the linear speed $v$. In fact, the clothes move in a circular motion against the water inside the basket. So, the water can easily clean the clothes. So, water escapes through the holes in the basket and can be drained away.
According to Newton’s second law, the force due to the gravity (Weight) is given by
$$
begin{align*}
F &= W \
&= m_{1} ~ a \
end{align*}
$$
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{E} }{ r^{2} } \
&= m_{1} ~ a \
&= G ~ dfrac{ m_{1} ~ m_{E} }{ r^{2} } \
end{align*}
$$
Rearrange and solve for the acceleration due to the gravity at the altitude of the International Space Station’s orbit:
$$
begin{align*}
a &= G ~ dfrac{ m_{E} }{r^{2} } \
end{align*}
$$
So, the acceleration due to the gravity at the altitude of the rotating space station’s orbit is sensual for its inhabitants. The inhabitants of the rotating space station on the outer rim should feel a force inward toward the center of the station in order to be on a circular path. This force that exerted by the floor on the inhabitants towards the station wall. Therefore, they feel like artificial gravity.
Solve for the figure $9.29$:
According to Newton’s second law in the horizontal direction:
$$
begin{align*}
f_{cp} &=m ~ a_{cp} \
&= f_{s}
end{align*}
$$
As Newton’s second law for circular motion, the centripetal force is given by the mass time the centripetal acceleration:
$$
begin{align*}
f_{cp} &= m ~ a_{cp} \
&= m ~ dfrac{ v^{2} }{ r} \
end{align*}
$$
So, the centripetal force is inversely proportional to the radius of the circular path and directly proportional to the speed of the car. Since the car’s speed is constant. Then the smaller radius has a greater centripetal force. As we know the larger force has a larger chance of skidding. So, the ranking in order of increasing likelihood that the car
might skid is $A> B> C$.
Since the car’s speed is constant, then the magnitude of the velocity is constant. But the velocity is a vector that depends on its magnitude and its direction. Since the direction of the car is always changeable tangential to the circular track. So, the answer is “No”.
Since the car’s speed is constant, then the magnitude of the velocity is constant. So, the answer is “Yes”.
Since the car’s speed is constant, then the magnitude of the velocity is constant. But the velocity is a vector that depends on its magnitude and its direction. Since the direction of the car is always changeable tangential to the circular track. In order to evaluate the acceleration, we use the following relation:
$$
begin{align*}
vec{a} &= dfrac{ Delta vec{v} }{ Delta t }
end{align*}
$$
So, the acceleration vector depends on the change in the velocity (as a vector) with respect to time. The change in the direction of the velocity is enough to generate linear acceleration. Therefore, the magnitude of the linear acceleration changes within the circular track. Therefore, the answer is “No”.
Since the car’s speed is constant, then the magnitude of the velocity is constant. But the velocity is a vector that depends on its magnitude and its direction. Since the direction of the car is always changeable tangential to the circular track. In order to evaluate the acceleration, we use the following relation:
$$
begin{align*}
vec{a} &= dfrac{ Delta vec{v} }{ Delta t }
end{align*}
$$
So, the acceleration vector depends on the change in the velocity (as a vector) with respect to time. The change in the direction of the velocity is enough to generate linear acceleration. Therefore, the direction of the linear acceleration changes within the circular track. Therefore, the answer is “No”.
(b) Yes.
(c) No.
(d) No.
The radius of the circular path is $r = 15 mathrm{~m}$. The centripetal accerlation is equal to $a_{cp} = 9 ~ g$.
$textbf{Required:}$
Finding linear speed of the capsule.
As textbook mentions the centripetal acceleration is given by the following relation
$$
begin{align*}
a_{cp,A} &= dfrac{ v^{2} }{ r} \
end{align*}
$$
Rearrange and solve for the linear speed of the capsule:
$$
begin{align*}
v &= sqrt{ a_{cp} ~ r } \
&= sqrt{ 9 times 9.8 mathrm{~m/s^{2}} times 15 mathrm{~m} } \
&= 36.373 mathrm{~m/s}
end{align*}
$$
So, the linear speed of the capsule is $36.373 mathrm{~m/s}$.
The radius of the rotating drum is $r = 0.31 mathrm{~m}$. The centripetal accerlation of the rim is equal to $a_{cp} = 27 mathrm{~m/s^{2}}$.
$textbf{Required:}$
Finding the tangential speed of the rim.
As textbook mentions the centripetal acceleration is given by the following relation
$$
begin{align*}
a_{cp,A} &= dfrac{ v^{2} }{ r} \
end{align*}
$$
Rearrange and solve for the tangential speed of the rim:
$$
begin{align*}
v &= sqrt{ a_{cp} ~ r } \
&= sqrt{ 27 mathrm{~m/s^{2}} times 0.31 mathrm{~m} } \
&= 2.893 mathrm{~m/s}
end{align*}
$$
So, the tangential speed of the rim is $2.893 mathrm{~m/s}$.
The distance from the bottom of the centrifuge to the axis of rotation is $r = 7.5 mathrm{~cm}$. The centripetal accerlation of the centrifuge is equal to $a_{cp} = 5.2 times 10^{4} ~ g$.
$textbf{Required:}$
Finding the linear speed of the test tube in the centrifuge.
As textbook mentions the centripetal acceleration is given by the following relation
$$
begin{align*}
a_{cp,A} &= dfrac{ v^{2} }{ r} \
end{align*}
$$
Rearrange and solve for the linear speed of the test tube in the centrifuge:
$$
begin{align*}
v &= sqrt{ a_{cp} ~ r } \
&= sqrt{ 5.2 times 10^{4} times 9.8 mathrm{~m/s^{2}} times 7.5 times 10^{-2} mathrm{~m} } \
&= 195.499 mathrm{~m/s}
end{align*}
$$
So, the linear speed of the test tube in the centrifuge is $195.499 mathrm{~m/s}$.
To find the force of static friction, assume it’s equal to the centripetal force:
$$
f_f=f_{cp}=mfrac{v^2}{r}
$$
Substitute the varibles with values given in the task:
$$
f_f=1400cdotfrac{18^2}{63}=7200:N=boxed{7.2:kN}
$$
f_f=7.2:kN
$$
The mass of the person is $m = 67 mathrm{~kg}$. The radius of curvature of the bump is $r = 35 mathrm{~m}$. The car’s speed is $v = 12 mathrm{~m/s}$.
$textbf{Required: }$
Finding the apparent weight.
According to Newton’s second law in the vertical direction:
$$
begin{align*}
sum F_{y} &= W – N \
&= – m ~ a_{cp} \
N &= W – m ~ a_{cp} \
end{align*}
$$
As textbook mentions the centripetal acceleration is given by the following relation
$$
begin{align*}
a_{cp} &= dfrac{ v^{2} }{ r} \
end{align*}
$$
Rearrange and solve for the apparent weight:
$$
begin{align*}
N &= W – m ~ a_{cp} \
&= m ~ g – m ~ dfrac{ v^{2} }{r} \
&= 67 mathrm{~kg} times 9.8 mathrm{~m/s^{2}} – 67 mathrm{~kg} times dfrac{ left( 12 mathrm{~m/s} right)^{2} }{ 35 mathrm{~m} } \
&= 380.943 mathrm{~N}
end{align*}
$$
So, the apparent weight is $380.943 mathrm{~N}$.
The mass of the person is $m = 67 mathrm{~kg}$. The radius of curvature of the bump is $r = 35 mathrm{~m}$.
$textbf{Required: }$
Finding the linear speed.
In order to feel weightless, the centripetal acceleration must be equal to the gravity due to Earth. As textbook mentions the centripetal acceleration is given by the following relation:
$$
begin{align*}
a_{cp,A} &= dfrac{ v^{2} }{ r} \
end{align*}
$$
Rearrange and solve for the tangential speed of the rim:
$$
begin{align*}
v &= sqrt{ a_{cp} ~ r } \
&= sqrt{ 9.8 mathrm{~m/s^{2}} times 35 mathrm{~m} } \
&= 18.52 mathrm{~m/s}
end{align*}
$$
So, the linear speed of the car above the circular cross-section is $18.52 mathrm{~m/s}$.
The mass of the Jill is $m = 63 mathrm{~kg}$. The length of the vine is $r = 6.9 mathrm{~m}$. The Vine’s speed is $v= 2.4 mathrm{~m/s}$.
$textbf{Required: }$
Finding the tension in the vine.
According to Newton’s second law in the vertical direction:
$$
begin{align*}
sum F_{y} &= W – T \
&= – m ~ a_{cp} \
T &= W – m ~ a_{cp} \
end{align*}
$$
As textbook mentions the centripetal acceleration is given by the following relation
$$
begin{align*}
a_{cp} &= dfrac{ v^{2} }{ r} \
end{align*}
$$
Rearrange and solve for the tension in the vine:
$$
begin{align*}
T &= W – m ~ a_{cp} \
&= m ~ g – m ~ dfrac{ v^{2} }{r} \
&= 63 mathrm{~kg} times 9.8 mathrm{~m/s^{2}} – 63 mathrm{~kg} times dfrac{ left( 2.4 mathrm{~m/s} right)^{2} }{ 6.9 mathrm{~m} } \
&= 564.809 mathrm{~N}
end{align*}
$$
So, the tension in the vine is $564.809 mathrm{~N}$.
Solve for the apparent weight at the top:
According to Newton’s second law in the vertical direction:
$$
begin{align*}
sum F_{y} &= – m ~ a_{cp} \
&= N_{top} – m ~ g \
end{align*}
$$
As textbook mentions the centripetal acceleration is given by the following relation
$$
begin{align*}
a_{cp} &= dfrac{ v^{2} }{ r} \
end{align*}
$$
Substituting from the previous calculations, then we get
$$
begin{align*}
N_{top} – m ~ g &= – m ~ a_{cp} \
end{align*}
$$
Rearrange and solve for the apparent weight at the top of the wheel:
$$
begin{align*}
N_{top} &= m ~ g – m ~ a_{cp} \
&= m ~ left( g – a_{cp} right) \
&= m ~ left( g – dfrac{ v^{2} }{ r } right) \
end{align*}
$$
Solve for the apparent weight at the bottom:
According to Newton’s second law in the vertical direction:
$$
begin{align*}
sum F_{y} &= m ~ a_{cp} \
&= N_{top} – m ~ g \
end{align*}
$$
As textbook mentions the centripetal acceleration is given by the following relation
$$
begin{align*}
a_{cp} &= dfrac{ v^{2} }{ r } \
&= dfrac{ v^{2} }{ r } \
end{align*}
$$
Substituting from the previous calculations, then we get
$$
begin{align*}
N_{bottom} – m ~ g &= m ~ a_{cp} \
end{align*}
$$
Rearrange and solve for the apparent weight at the bottom of the wheel:
$$
begin{align*}
N_{bottom} &= m ~ g + m ~ a_{cp} \
&= m ~ left( g + a_{cp} right) \
&= m ~ left( g + dfrac{ v^{2} }{ r } right) \
end{align*}
$$
So, the main factor that makes a difference between the two apparent weights is the direction of the centripetal force in each case.
In order to evaluate the angular speed of the wheel, we use the following relation:
$$
begin{align*}
omega &= dfrac{v}{r} \
&= dfrac{ 2 pi }{ T}
end{align*}
$$
Rearrange and solve speed of the wheel:
$$
begin{align*}
v&= dfrac{ 2 pi ~ r }{T }\
&= dfrac{ 2 pi times 7.2 mathrm{~m} }{28 mathrm{~s} } \
&= 1.616 mathrm{~m/s}
end{align*}
$$
Solve for the apparent weight at the top:
From part (a), the apparent weight at the top of the wheel:
$$
begin{align*}
N_{top} &= m ~ g – m ~ a_{cp} \
&= m ~ left( g – a_{cp} right) \
&= m ~ left( g – dfrac{ v^{2} }{ r } right) \
&= 55 mathrm{~kg} times left( 9.8 mathrm{~m/s^{2}} – dfrac{ left( 1.616 mathrm{~m/s} right)^{2} }{ 7.2 mathrm{~m} } right) \
&= 519.05 mathrm{~N}
end{align*}
$$
So, apparent weight at the top is $519.05 mathrm{~N}$.
Solve for the apparent weight at the top:
From part (a), the apparent weight at the bottom of the wheel:
$$
begin{align*}
N_{bottom} &= m ~ g + m ~ a_{cp} \
&= m ~ left( g + a_{cp} right) \
&= m ~ left( g + dfrac{ v^{2} }{ r } right) \
&= 55 mathrm{~kg} times left( 9.8 mathrm{~m/s^{2}} + dfrac{ left( 1.616 mathrm{~m/s} right)^{2} }{ 7.2 mathrm{~m} } right) \
&= 558.949 mathrm{~N}
end{align*}
$$
So, the apparent weight at the bottom of the wheel is $558.949 mathrm{~N}$.
(b) The apparent weight at the top is $519.05 mathrm{~N}$ and the apparent weight at the bottom of the wheel is $558.949 mathrm{~N}$.
According to Kepler’s second law which assigns that as a planet moves in its orbit, it sweeps out an equal amount of area in an equal amount of time. As we know the radius of Mars is approximately half of the radius of Earth. So, Mars’s orbit sweeps out area differs from Earth’s orbit sweeps out area. Therefore, the answer is “No, The radius of Mars doesn’t sweep out the same amount of area per time as that of Earth.”
According to Kepler’s second law which assigns that as a planet moves in its orbit, it sweeps out an equal amount of area in an equal amount of time. As the problem mentions the planet sweeps out the area $A$ in $2$ months. Therefore, the planet sweeps out the area $dfrac{1}{2} ~ A$ in $1$ months. Also, The planet sweeps out the area $dfrac{3}{2} ~A$ in $3$ months.
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{2} }{ r^{2} } \
end{align*}
$$
As we know the free-falling of the satellite means that the only force that acts on the satellite is the gravitational force due to Earth Which keeps the satellite in its orbital and doesn’t crash to the ground. So, Friend $1$ is correct.
As the textbook mentions Kepler’s third law that studied the relation between the distance of a satellite from the Earth and its orbital period which is given by
$$
begin{align*}
T &= left( dfrac{ 2 pi }{ sqrt{ G ~ M_{S} } } right) ~ r^{dfrac{3}{2}} \
end{align*}
$$
Once we are able to calculate the orbit period the radius of a satellite can be measured. The mass of the planet can be calculated using Kepler’s third law.
In practice, the mass of Charon is large compared to the mass of Pluto, so that Kepler’s third law in the form given in the text had to be adjusted to account for the motions of the two bodies about their center of mass.
In practice, the mass of Charon is large compared to the mass of Pluto, so that Kepler’s third law in the form given in the text had to be adjusted to account for the motions of the two bodies about their center of mass.
As we know the acceleration due to gravity on the surface of the Moon is in range from $0.0253 mathrm{~m/s^{2}}$ to $1.625 mathrm{~m/s^{2}}$. If you can climb a lunar mountain and throw a rock horizontally from its summit. The acceleration due to gravity that affects the rock is minimum (we can neglect it). Since there is no atmosphere to slow a projectile on the Moon. If you throw the rock sufficiently fast with a velocity of $1680 mathrm{~m/s}$, then it will orbit the Moon in about $1.8 mathrm{~hr}$ and might hit you in the back.
The mass of Earth is $M_{E} = 5.972 times 10^{24} mathrm{~kg}$. The mass of the Sun is $M_{S} = 1.989 times 10^{30} mathrm{~kg}$. The mass of the Moon is $M_{M} = 7.348 times 10^{22} mathrm{~kg}$. The distance between the Sun and Earth is $R_{S,E} = 1.481 times 10^{11} mathrm{~m}$.The distance between the Sun and Moon is $R_{S,M} = 3.844 times 10^{8} mathrm{~m}$.
Solve for the Earth’s case:
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F_{E} &= G ~ dfrac{ M_{E} ~ M_{S} }{ R_{S,E}^{2} } \
&= 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} ~ dfrac{ 5.972 times 10^{24} mathrm{~kg} times 1.989 times 10^{30} mathrm{~kg} }{ left( 1.481 times 10^{11} mathrm{~m} right)^{2} } \
&= 3.612 times 10^{22} mathrm{~N}
end{align*}
$$
Solve for the Moon’s case:
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F_{M} &= G ~ dfrac{ M_{M} ~ M_{E} }{ R_{E,M}^{2} } \
&= 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} ~ dfrac{ 7.348 times 10^{22} mathrm{~kg} times 5.972 times 10^{24} mathrm{~kg} }{ left(3.844 times 10^{8} mathrm{~m} right)^{2} } \
&=1.98 times 10^{20} mathrm{~N}
end{align*}
$$
Since the exerted force on the Moon by the Sun is twice the force exerted by the Earth on The Moon. So, the resultant force is equal to the force exerted by the Earth on The Moon but due to the Sun-Moon force’s direction. Therefore, the Moon Should orbit about the Sun.
According to Kepler’s third law $T=(constant)r^{3/2}$. By increasing the orbit radius $r$ will result in increase of the orbit period $T$. We reach the conclusion that the length of the month will increase.
Earth’s radius is $R_{E} = 6.37 times 10^{6} mathrm{~m}$. The height of the satellite above the Earth is $h = 2.02 times 10^{7} mathrm{~m}$. The mass of Earth is $m_{E} = 5.972 times 10^{24} mathrm{~kg}$.
$textbf{Required: }$
Finding the orbital period of the satellite.
As the textbook mentions Kepler’s third law that studied the relation between the distance of a satellite from the Earth and its orbital period which is given by
$$
begin{align*}
T &= left( dfrac{ 2 pi }{ sqrt{ G ~ M_{S} } } right) ~ r^{dfrac{3}{2}} \
T &= left( dfrac{ 2 pi }{ sqrt{ G ~ M_{M} } } right) ~ r^{dfrac{3}{2}} \
&= left( dfrac{ 2 pi }{ sqrt{ G ~ M_{M} } } right) ~ left(R_{M} + h right)^{dfrac{3}{2}} \
&= left( dfrac{ 2 pi }{ sqrt{ 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} times 5.972 times 10^{24} mathrm{~kg}} } right) ~ left( 6.37 times 10^{6} mathrm{~m} + 2.02 times 10^{7} mathrm{~m} right)^{dfrac{3}{2}} \
&= 4.3124 times 10^{4} mathrm{~s}
end{align*}
$$
So, the orbital period of the satellite is $4.3124 times 10^{4} mathrm{~s}$.
The period that that planet takes to rotate about Iota Horologii is $T = 320 mathrm{~days}$. The mass of the Iota Horologii that is equal to the mass of the Sun is $M_{s} = 1.989 times 10^{30} mathrm{~kg}$.
$textbf{Required: }$
Finding the average radius of the Planet’s orbit.
As the textbook mentions Kepler’s third law that studied the relation between the distance of a planet from the Sun and its orbital period which is given by
$$
begin{align*}
T &= left( dfrac{ 2 pi }{ sqrt{ G ~ M_{S} } } right) ~ r^{dfrac{3}{2}} \
end{align*}
$$
Rearrange and solve for the average distance from the Sun:
$$
begin{align*}
r^{dfrac{3}{2}} &= dfrac{ T }{ left( dfrac{ 2 pi }{ sqrt{ G ~ M_{S} } } right) } \
r &= left( dfrac{ T }{ left( dfrac{ 2 pi }{ sqrt{ G ~ M_{S} } } right) } right)^{dfrac{2}{3}} \
&= left( dfrac{ T ~ sqrt{ G ~ M_{S} } }{ 2 pi } right)^{dfrac{2}{3}} \
&= left( dfrac{ 320 times 24 times 60 times 60 mathrm{~s} times sqrt{ 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} times 1.989 times 10^{30} mathrm{~kg} } }{ 2 pi } right)^{dfrac{2}{3}} \
&= 1.369 times 10^{11} mathrm{~m}
end{align*}
$$
So, the average radius of the planet’s orbit is $1.369 times 10^{11} mathrm{~m}$.
The separation between Phobos and Mars is $r = 9.378 times 10^{6} mathrm{~m}$. The mass of Mars is $m_{m} = 6.39 times 10^{23} mathrm{~kg}$.
$textbf{Required: }$
Finding the orbital period of Phobos.
As the textbook mentions Kepler’s third law that studied the relation between the distance of Phobos from the Mars and its orbital period which is given by
$$
begin{align*}
T &= left( dfrac{ 2 pi }{ sqrt{ G ~ m_{m} } } right) ~ r^{dfrac{3}{2}} \
T &= left( dfrac{ 2 pi }{ sqrt{ G ~ m_{m} } } right) ~ r^{dfrac{3}{2}} \
&= left( dfrac{ 2 pi }{ sqrt{ 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} times 6.39 times 10^{23} mathrm{~kg}} } right) ~ left( 9.378 times 10^{6} mathrm{~m} right)^{dfrac{3}{2}} \
&= 2.764 times 10^{4} mathrm{~s}
end{align*}
$$
So, the orbital period of Phobos is $2.764 times 10^{4} mathrm{~s}$.
The distance from the center of Jupiter and Ganymede is $r = 1.07 times 10^{9} mathrm{~m}$. The orbital period of Ganymede is $T = 6.18 times 10^{5} mathrm{~s}$.
$textbf{Required: }$
Finding the mass of Jupiter.
As the textbook mentions Kepler’s third law that studied the relation between the distance of a planet from the Sun and its orbital period which is given by
$$
begin{align*}
T &= left( dfrac{ 2 pi }{ sqrt{ G ~ M_{J} } } right) ~ r^{dfrac{3}{2}} \
end{align*}
$$
Rearrange and solve for the mass of Jupiter:
$$
begin{align*}
dfrac{T}{ r^{dfrac{3}{2}} } &= dfrac{ 2 pi }{ sqrt{ G ~ M_{J} } } \
M_{J} &= dfrac{ left( dfrac{ 2 pi ~ r^{dfrac{3}{2}} }{T} right)^{2} }{G} \
&= dfrac{ left( dfrac{ 2 pi ~ left( 1.07 times 10^{9} mathrm{~m} right)^{dfrac{3}{2}} }{6.18 times 10^{5} mathrm{~s}} right)^{2} }{6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}}} \
&= 1.8985 times 10^{27} mathrm{~kg}
end{align*}
$$
So, the mass of Jupiter is $1.8985 times 10^{27} mathrm{~kg}$.
Earth’s radius is $R_{E} = 6.37 times 10^{6} mathrm{~m}$. The height of the satellite above the Earth is $h = 2 ~ R_{E}$. The mass of Earth is $m_{E} = 5.972 times 10^{24} mathrm{~kg}$.
$textbf{Required: }$
(a) Finding the orbital period of the satellite.
(b) Finding if the answer in part (a) depends on the satellites mass.
As the textbook mentions Kepler’s third law that studied the relation between the distance of a satellite from the Earth and its orbital period which is given by
$$
begin{align*}
T &= left( dfrac{ 2 pi }{ sqrt{ G ~ M_{S} } } right) ~ r^{dfrac{3}{2}} \
T &= left( dfrac{ 2 pi }{ sqrt{ G ~ M_{M} } } right) ~ r^{dfrac{3}{2}} \
&= left( dfrac{ 2 pi }{ sqrt{ G ~ M_{M} } } right) ~ left(R_{M} + h right)^{dfrac{3}{2}} \
&= left( dfrac{ 2 pi }{ sqrt{ G ~ M_{M} } } right) ~ left(R_{M} + 2 ~ R_{E} right)^{dfrac{3}{2}} \
&= left( dfrac{ 2 pi }{ sqrt{ G ~ M_{M} } } right) ~ left(3 R_{M} right)^{dfrac{3}{2}} \
&= left( dfrac{ 2 pi }{ sqrt{ 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} times 5.972 times 10^{24} mathrm{~kg}} } right) ~ left(3 times 6.37 times 10^{6} mathrm{~m} right)^{dfrac{3}{2}} \
&= 2.6304 times 10^{4} mathrm{~s}
end{align*}
$$
So, the orbital period of the satellite is $2.6304 times 10^{4} mathrm{~s}$.
As we see in part (a), the orbital period of the satellite is $2.6304 times 10^{4} mathrm{~s}$ and it doesn’t depend on the satellite’s mass.
(b) The orbital period of the satellite is $2.6304 times 10^{4} mathrm{~s}$ and it doesn’t depend on the satellite’s mass.
The mass of Mars is $m_{m} = 6.39 times 10^{23} mathrm{~kg}$.
$textbf{Required: }$
(a) Finding if Deimos closer to or farther from Mars than Phobos.
(b) Finding the separation from the center of Mars and Deimos, if the orbital period of Deimos is $1.1 times 10^{5} mathrm{~s}$.
As the textbook mentions Kepler’s third law that studied the relation between the distance of a planet from the Sun and its orbital period which is given by
$$
begin{align*}
T &= left( dfrac{ 2 pi }{ sqrt{ G ~ m_{m} } } right) ~ r^{dfrac{3}{2}} \
end{align*}
$$
Rearrange and solve for the average distance from the Sun:
$$
begin{align*}
r^{dfrac{3}{2}} &= dfrac{ T }{ left( dfrac{ 2 pi }{ sqrt{ G ~ m_{m} } } right) } \
r &= left( dfrac{ T }{ left( dfrac{ 2 pi }{ sqrt{ G ~ m_{m} } } right) } right)^{dfrac{2}{3}} \
&= left( dfrac{ T ~ sqrt{ G ~ m_{m} } }{ 2 pi } right)^{dfrac{2}{3}} \
end{align*}
$$
So, the distance between Deimos and Mars is independent of Diemos’ mass. As we see in the previous calculations, the distance between Deimos and Mars is directly proportional to the orbital period of Demos $r ~ alpha ~ T^{dfrac{2}{3}}$. Therefore, Deimos is closer to Mars than Phobos.
As the textbook mentions Kepler’s third law that studied the relation between the distance of a moon from the Mars and its orbital period which is given by
$$
begin{align*}
T &= left( dfrac{ 2 pi }{ sqrt{ G ~ m_{m} } } right) ~ r^{dfrac{3}{2}} \
end{align*}
$$
Rearrange and solve for the average distance from the Sun:
$$
begin{align*}
r^{dfrac{3}{2}} &= dfrac{ T }{ left( dfrac{ 2 pi }{ sqrt{ G ~ m_{m} } } right) } \
r &= left( dfrac{ T }{ left( dfrac{ 2 pi }{ sqrt{ G ~ m_{m} } } right) } right)^{dfrac{2}{3}} \
&= left( dfrac{ T ~ sqrt{ G ~ m_{m} } }{ 2 pi } right)^{dfrac{2}{3}} \
&= left( dfrac{1.1 times 10^{5} mathrm{~s} times sqrt{ 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} times 6.39 times 10^{23} mathrm{~kg} } }{ 2 pi } right)^{dfrac{2}{3}} \
&= 2.355 times 10^{7} mathrm{~m}
end{align*}
$$
So, the average distance from the center of Mars and Demos’ orbit is $2.355 times 10^{7} mathrm{~m}$.
(b) The average distance from the center of Mars and Demos’ orbit is $2.355 times 10^{7} mathrm{~m}$.
Earth’s radius is $R_{E} = 6.37 times 10^{6} mathrm{~m}$. The height of the satellite above the Earth is $h = 3.58 times 10^{7} mathrm{~m}$. The mass of Earth is $m_{E} = 5.972 times 10^{24} mathrm{~kg}$.
$textbf{Required: }$
Finding the speed of the satellite.
As the textbook mentions Kepler’s third law that studied the relation between the distance of a planet from the Sun and its orbital period which is given by
$$
begin{align*}
T &= left( dfrac{ 2 pi }{ sqrt{ G ~ M_{S} } } right) ~ r^{dfrac{3}{2}} \
end{align*}
$$
Similarly, the speed of the satellite that orbiting Earth is given by
$$
begin{align*}
v &= sqrt{ dfrac{ G ~ M_{E} }{ r } }\
&= sqrt{ dfrac{ G ~ M_{E} }{ R_{E} + h } } \
&= sqrt{ dfrac{ 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} times 5.972 times 10^{24} mathrm{~kg} }{ 6.37 times 10^{6} mathrm{~m} +3.58 times 10^{7} mathrm{~m} mathrm{~m} } }\
&= 3.073 times 10^{3} mathrm{~m/s}
end{align*}
$$
So, the speed of the satellite is $3.073 times 10^{3} mathrm{~m/s}$.
Earth’s radius is $R_{E} = 6.37 times 10^{6} mathrm{~m}$. The distance between Earth and Sun is $r = 1.4804 times 10^{11} mathrm{~m}$. The mass of Sun is $M_{S} = 1.989 times 10^{30} mathrm{~kg}$.
$textbf{Required: }$
Finding the speed of Earth around the Sun.
As the textbook mentions Kepler’s third law that studied the relation between the distance of a planet from the Sun and its orbital period which is given by
$$
begin{align*}
T &= left( dfrac{ 2 pi }{ sqrt{ G ~ M_{S} } } right) ~ r^{dfrac{3}{2}} \
end{align*}
$$
Similarly, the speed of the satellite that orbiting Earth is given by
$$
begin{align*}
v &= sqrt{ dfrac{ G ~ M_{S} }{ r } }\
&= sqrt{ dfrac{ G ~ M_{S} }{ R_{E} + h } } \
&= sqrt{ dfrac{ 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} times 1.989 times 10^{30} mathrm{~kg} }{ 1.4804 times 10^{11} mathrm{~m} } }\
&= 2.994 times 10^{4} mathrm{~m/s}
end{align*}
$$
So, the speed of the Earth’s orbital about Sun is $2.994 times 10^{4} mathrm{~m/s}$.
The distance from Dactyl and Ida is $r = 8.9 times 10^{4} mathrm{~m}$. The orbital period of Dactyl is $T = 19 mathrm{~hr}$.
$textbf{Required: }$
(a) Finding the mass of Ida Strategy.
(b) Finding the mass of Ida.
As the textbook mentions Kepler’s third law that studied the relation between the distance of a planet from the Sun and its orbital period which is given by
$$
begin{align*}
T &= left( dfrac{ 2 pi }{ sqrt{ G ~ M_{I} } } right) ~ r^{dfrac{3}{2}} \
end{align*}
$$
Rearrange and solve for the mass of Jupiter:
$$
begin{align*}
dfrac{T}{ r^{dfrac{3}{2}} } &= dfrac{ 2 pi }{ sqrt{ G ~ M_{I} } } \
M_{I} &= dfrac{ left( dfrac{ 2 pi ~ r^{dfrac{3}{2}} }{T} right)^{2} }{G} \
end{align*}
$$
The strategy is firstly, using Kepler’s third law to deduce a formula for the mass of Ida in terms of the orbital period of Dactyl and the distance from Dactyl and Ida.
As the textbook mentions Kepler’s third law that studied the relation between the distance of a planet from the Sun and its orbital period which is given by
$$
begin{align*}
T &= left( dfrac{ 2 pi }{ sqrt{ G ~ M_{I} } } right) ~ r^{dfrac{3}{2}} \
end{align*}
$$
Rearrange and solve for the mass of Jupiter:
$$
begin{align*}
dfrac{T}{ r^{dfrac{3}{2}} } &= dfrac{ 2 pi }{ sqrt{ G ~ M_{I} } } \
M_{I} &= dfrac{ left( dfrac{ 2 pi ~ r^{dfrac{3}{2}} }{T} right)^{2} }{G} \
&= dfrac{ left( dfrac{ 2 pi ~ left( 8.9 times 10^{4} mathrm{~m} right)^{dfrac{3}{2}} }{19 times 60 times 60 mathrm{~s}} right)^{2} }{6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}}} \
&= 8.918 times 10^{16} mathrm{~kg}
end{align*}
$$
So, the mass of Ida is $8.918 times 10^{16} mathrm{~kg}$.
(b) The mass of Ida is $8.918 times 10^{16} mathrm{~kg}$.
textbf{Concept:}
$$
By conducting dimensional analysis, converting G into its fundamental dimensions, and observing that ME has the dimension of mass and r has the dimension of length.
$$
textbf{Solution:}
$$
Split $G$ into its basic dimensions
$$
G=6.67times 10^{-11} N.m^2/kg^2
$$
$$
displaystylefrac{(force)(length)^2}{(mass)^2}=frac{[masstimes acceleration](length)^2}{(mass)^2}
$$
$$
frac{[(mass)timesdisplaystylefrac{(length)}{(time)^2}(length)^2}{(mass)^2}=frac{(length)^2}{(mass)times (time)^2}
$$
Now add up the dimensions of $G$ with those of $M_E$ and $r$ to get dimensions of $(length/time)^2$
$$
frac{GM_E}{r}=bigg(frac{(length)^{cancel{3}/2}times cancel{(mass)}}{cancel{(mass)}(time)^2}bigg)frac{1}{cancel{(length)}}=frac{(length)^2}{(time)^2}
$$
Then square root the equation to find $v$
$$
v=sqrt{frac{GM_E}{r}}=sqrt{frac{(length)^2}{(time)^2}}=frac{length}{time}Rightarrow boxed{bf color{#4257b2} v=sqrt{frac{GM_E}{r}}}
$$
v=sqrt{frac{GM_E}{r}}
$$
Earth’s radius is $R_{E} = 6.37 times 10^{6} mathrm{~m}$. The height of the satellite above the Earth is $h = R_{E}$. The mass of Earth is $m_{E} = 5.972 times 10^{24} mathrm{~kg}$.
$textbf{Required: }$
Finding the speed of the satellite.
As the textbook mentions Kepler’s third law that studied the relation between the distance of a planet from the Sun and its orbital period which is given by
$$
begin{align*}
T &= left( dfrac{ 2 pi }{ sqrt{ G ~ M_{S} } } right) ~ r^{dfrac{3}{2}} \
end{align*}
$$
Similarly, the speed of the satellite that orbiting Earth is given by
$$
begin{align*}
v &= sqrt{ dfrac{ G ~ M_{E} }{ r } }\
&= sqrt{ dfrac{ G ~ M_{E} }{ R_{E} + h } } \
end{align*}
$$
So, the speed of the satellite is inversely proportional to the square root of the altitude $v ~ alpha ~ dfrac{1}{sqrt{r} }$. Since satellite 1 at a greater altitude than satellite 2, then satellite 1 has speed less than the speed of satellite 2.
As the textbook mentions Kepler’s third law that studied the relation between the distance of a satellite from Earth and its orbital period which is given by
$$
begin{align*}
T &= left( dfrac{ 2 pi }{ sqrt{ G ~ M_{S} } } right) ~ r^{dfrac{3}{2}} \
end{align*}
$$
Similarly, the speed of the satellite that orbiting Earth is given by
$$
begin{align*}
v &= sqrt{ dfrac{ G ~ M_{E} }{ r } }\
&= sqrt{ dfrac{ G ~ M_{E} }{ R_{E} + h } } \
&= sqrt{ dfrac{ 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} times 5.972 times 10^{24} mathrm{~kg} }{ 6.37 times 10^{6} mathrm{~m} +6.37 times 10^{6} mathrm{~m} mathrm{~m} } }\
&= 5.592 times 10^{3} mathrm{~m/s}
end{align*}
$$
So, the speed of the satellite is $5.592 times 10^{3} mathrm{~m/s}$.
(b) The speed of the satellite is $5.592 times 10^{3} mathrm{~m/s}$.
Assume you fly to the east in direction of Earth’s rotation, you will experience a greater speed relative to the centre of Earth as compared to if you fly to the west. The result is the centripetal force required to maintain your circular motion is greater, and your apparent weight is less. We reach the conclude that the reading on the scale will $boxed{ bf color{#4257b2}increase}$ slightly when the air plane turns around and heads due west with the same speed relative to Earth’s surface.
As the textbook mentions Kepler’s third law that studied the relation between the distance of the satellite from Earth and its orbital period which is given by
$$
begin{align*}
T &= left( dfrac{ 2 pi }{ sqrt{ G ~ M_{S} } } right) ~ r^{dfrac{3}{2}} \
end{align*}
$$
Similarly, the speed of the satellite that orbiting Earth is given by
$$
begin{align*}
v &= sqrt{ dfrac{ G ~ M_{E} }{ r } }\
end{align*}
$$
So, the speed of the satellite is depending on the mass of Earth and the separation between the satellite and Earth. But the speed of the satellite independent of the satellite’s mass. So, Is the orbital speed of the small satellite equal to the orbital speed of the space station.
As the textbook mentions Kepler’s third law that studied the relation between the distance of a satellite from the Planet and its orbital period which is given by
$$
begin{align*}
T &= left( dfrac{ 2 pi }{ sqrt{ G ~ M_{S} } } right) ~ r^{dfrac{3}{2}} \
end{align*}
$$
Similarly, the speed of the satellite that orbiting Earth is given by
$$
begin{align*}
v &= sqrt{ dfrac{ G ~ M_{S} }{ r } }\
end{align*}
$$
So, the orbital speed is inversely proportional to the square root of the distance. So, if the distance increases, then the orbital speed will decrease.
The diameter of the screen is $0.39 mathrm{~m}$. The linear speed at the rim of the screen is $v = 35 mathrm{~m/s}$.
$textbf{Required: }$
Finding the centripetal acceleration at the rim of the screen.
As textbook mentions the centripetal acceleration is given by the following relation
$$
begin{align*}
a_{cp} &= dfrac{ v^{2} }{ r} \
&= dfrac{ left( 35 mathrm{~m/s} right)^{2} }{ dfrac{0.39 mathrm{~m} }{2} } \
&= 6.282 times 10^{3} mathrm{~m/s^{2}}
end{align*}
$$
So, the centripetal acceleration at the rim of the screen is $6.282 times 10^{3} mathrm{~m/s^{2}}$.
The centripetal acceleration of the ball is $a_{cp} = 250 mathrm~{m/s^{2}}$. The ball’s speed is $v = 2.3 mathrm{~m/s}$.
$textbf{Required: }$
Finding the radius of the ball.
As textbook mentions the centripetal acceleration is given by the following relation
$$
begin{align*}
a_{cp,A} &= dfrac{ v^{2} }{ r} \
end{align*}
$$
Rearrange and solve for the radius of the corner:
$$
begin{align*}
r &= dfrac{ v^{2} }{a_{cp,A}} \
&= dfrac{ left( 2.3 mathrm{~m/s} right)^{2} }{ 250 mathrm{~m/s^{2}} } \
&= 0.021 mathrm{~m} \
&= 2.116 mathrm{~cm}
end{align*}
$$
So, the radius of the ball is $2.116 mathrm{~cm}$.
As the Skylab’s orbit’s radius decreases, its speed did $boxed{ bf color{#4257b2}increase}$ as the gain in its kinetic energy due to the loss of gravitational potential energy was much larger than the loss of its kinetic energy due to friction. Yet another way approach is that the orbit speed of a satellite is given by $v=sqrt(GM/r^)$, so that the speed increases with decreasing radius.
textbf{Concept:}
$$
The radius of the plant is much more larger then height of the astronauts’ jump, so we assume that the acceleration of gravity is constant during the jump. Applying conservation of mechanical energy to find an expression for the acceleration of gravity as a function of the initial speed and the maximum jump height, and set it equal to $GM/R^2$ . Later solve for the mass $M$ of the planet.
$$
textbf{Solution:}
$$
Assume $E_i=E_f$ and solve for $g$
$$
KE_i+PE_i=KE_f+PE_f
$$
$$
frac{1}{2}mv_i^2+0=0+mgh
$$
$$
g=v_i^2/2h
$$
Now LET $g=GM/R^2$ and solve for $M$
$$
v_i^2/2h=GM/R^2
$$
$$
M=frac{R^2v_i^2}{2Gh}=frac{(3860times10^3m)^2(3.10m/s)^2}{2(6.67times 10^{-11} N.m^2/kg^2)(0.580m)}=boxed{ bf color{#4257b2}1.85times10^{24}kg}
$$
M=1.85times10^{24}kg
$$
The radius of the merry-go-round is $r = 2.3 mathrm{~m}$. The child’s speed is $v= 2.2 mathrm{~m/s}$.
$textbf{Required: }$
Finding the minimum static friction coefficient.
According to Newton’s second law in the vertical direction:
$$
begin{align*}
sum F_{y} &= W – N \
&= 0 \
W &= N \
end{align*}
$$
According to Newton’s second law in the horizontal direction:
$$
begin{align*}
sum F_{x} &=m ~ a\
&= f_{s}
end{align*}
$$
As textbook mentions the centripetal acceleration is given by the following relation
$$
begin{align*}
a_{cp,A} &= dfrac{ v^{2} }{ r} \
&= dfrac{ left( 1 mathrm{~m/s} right)^{2} }{ 5 mathrm{~m} } \
&= 0.2 mathrm{~m/s^{2}}
end{align*}
$$
Substituting from the previous calculation, then we get
$$
begin{align*}
f_{s} &= m ~ a \
&= m ~ dfrac{ v^{2} }{ r} \
&= mu_{s} ~ N \
&= mu_{s} ~ W \
&= mu_{s} ~ m ~ g \
end{align*}
$$
Rearrange and solve for the minimum coefficient of static friction:
$$
begin{align*}
mu_{s} &= dfrac{ v^{2} }{ r ~ g } \
&= dfrac{ left( 2.2 mathrm{~m/s} right)^{2} }{ 2.3 mathrm{~m} times 9.8 mathrm{~m/s^{2}} } \
&= 0.215
end{align*}
$$
So, the minimum coefficient of static friction is $0.215$.
The Matian’s day is $T = 24.6229 mathrm{~hr}$. The mass of the Mars is $m_{m} = 6.4 times 10^{23} mathrm{~kg}$.
$textbf{Required: }$
Finding the average distance from surface of Mars to the satellite.
As the textbook mentions Kepler’s third law that studied the relation between the distance of a planet from the Sun and its orbital period which is given by
$$
begin{align*}
T &= left( dfrac{ 2 pi }{ sqrt{ G ~ m_{m} } } right) ~ r^{dfrac{3}{2}} \
end{align*}
$$
Rearrange and solve for the average distance from the Sun:
$$
begin{align*}
r^{dfrac{3}{2}} &= dfrac{ T }{ left( dfrac{ 2 pi }{ sqrt{ G ~ m_{m} } } right) } \
r &= left( dfrac{ T }{ left( dfrac{ 2 pi }{ sqrt{ G ~ m_{m} } } right) } right)^{dfrac{2}{3}} \
&= left( dfrac{ T ~ sqrt{ G ~ M_{S} } }{ 2 pi } right)^{dfrac{2}{3}} \
&= left( dfrac{ 24.6229 times 60 times 60 mathrm{~s} times sqrt{ 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} times 6.4 times 10^{23} mathrm{~kg} } }{ 2 pi } right)^{dfrac{2}{3}} \
&= 2.041 times 10^{7} mathrm{~m}
end{align*}
$$
Since the radius of Mars is $3.3895 times 10^{3} mathrm{~km}$, the average distance from the surface of Mars to the satellite is $2.041 times 10^{7} mathrm{~m} – 3.3895 times 10^{6} mathrm{~m} = 1.702 times 10^{7} mathrm{~m}$.
According to Newton’s second law in the vertical direction:
$$
begin{align*}
sum F_{y} &= W – T \
&= 0 \
T &= W \
end{align*}
$$
As textbook mentions the centripetal acceleration is given by the following relation
$$
begin{align*}
a_{cp} &= dfrac{ v^{2} }{ r} \
end{align*}
$$
Rearrange and solve for the speed of the hockey:
$$
begin{align*}
W &= m ~ a_{cp} \
&= m ~ dfrac{ v^{2} }{r} \
&= M ~ g \
v &= sqrt{ dfrac{ M ~ g ~ r }{ m } } \
end{align*}
$$
So, the speed of the hockey is $sqrt{ dfrac{ M ~ g ~ r }{ m } }$.
From figure $9.36$, when the radius of the comet is $2.7 mathrm{~km}$, then the corresponding acceleration due to gravity (g) from the curve I is $0.00005 ~ g$ and the corresponding acceleration due to gravity (g) from the curve II is $0.0001 ~ g$. So, curve II is the correct curve to describe the experiment. The answer is “B. Curve II”.
As textbook mentions the centripetal acceleration is given by the following relation
$$
begin{align*}
a_{cp,A} &= dfrac{ v^{2} }{ r} \
end{align*}
$$
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{2} }{ r^{2} } \
&= m_{1} ~ a \
end{align*}
$$
Rearrange and solve for the mass of Comet wild $2$:
$$
begin{align*}
m_{2} &= dfrac{ a ~ r^{2} }{ G } \
&= dfrac{ 0.0001 ~ g ~ r^{2} }{ G } \
&= dfrac{ 0.0001 times 9.8 mathrm{~m/s^{2}} times left( 2.7 times 10^{3} mathrm{~m} right)^{2} }{ 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} } \
&= 1.071 times 10^{14} mathrm{~kg}
end{align*}
$$
So, the mass of Comet wild $2$ is $1.071 times 10^{14} mathrm{~kg}$. Therefore, the answer is C. $1.1 times 10^{14} mathrm{~kg}$.
The mass of the Comet is $m = 1.1 times 10^{14} mathrm{~kg}$. The radius of the comet is $r = 2.7 times 10^{3} mathrm{~m}$. The height of the satellite above the comet is $h = 2 r$.
$textbf{Required: }$
Finding the period of completing one cycle that it take for the satellite to complete one orbit about the comet.
As the textbook mentions Kepler’s third law that studied the relation between the distance of a satellite from the comet and its orbital period which is given by
$$
begin{align*}
T &= left( dfrac{ 2 pi }{ sqrt{ G ~ m } } right) ~ R^{dfrac{3}{2}} \
&= left( dfrac{ 2 pi }{ sqrt{ G ~ m } } right) ~ left( 2 r right)^{dfrac{3}{2}} \
&= left( dfrac{ 2 pi }{ sqrt{ 6.67 times 10^{-11} mathrm{~N cdot m^{2}/kg^{2}} times 1.1 times 10^{14} mathrm{~kg}} } right) ~ left( 2 times 2.7 times 10^{3} mathrm{~m} right)^{dfrac{3}{2}} \
&= 2.911 times 10^{4} mathrm{~s} \
&= 5.3475 times 10^{4} mathrm{~s} times dfrac{1}{60 times 60} mathrm{~h/s} \
&= 8.2 mathrm{~h}
end{align*}
$$
So, the period of completing one cycle that it takes for the satellite to complete one orbit about the comet $8.2 mathrm{~h}$. Therefore, the answer is D. $8.2 mathrm{~h}$.

