
All Solutions
Page 260: Assessment
As the textbook mentions that the initial momentum of the ball is given by the mass times the velocity.
$$
begin{align*}
vec{p} &= m ~ vec{v} \
end{align*}
$$
Since the momentum is depending on the mass and the velocity. So, it is possible to find a truck that has zero momentum, if the truck was at rest.
$$
begin{align*}
vec{p_{truck}} &= m_{truck} ~ vec{v_{truck}} \
&= m times 0 mathrm{~m/s} \
&= 0 mathrm{~kg cdot m/s}
end{align*}
$$
So, if the baseball moves with any velocity, then the baseball will have momentum greater than truck’s momentum. Therefore, the answer is yes, it is possible for a baseball to have more momentum than a truck.
In order to evaluate the kinetic energy of a particle, we use the following relation:
$$
begin{align*}
K.E &= dfrac{1}{2} ~ m ~ v^{2} \
end{align*}
$$
As we know the kinetic energy is a scalar depends only on the magnitude and there are no particles that have zero mass. So, if the kinetic energy of a system of particles is zero, then the speed of each particle in the system is zero, too. That’s mean no particles in the system is moving.
As the textbook mentions that the momentum of the system is given by the mass times the velocity.
$$
begin{align*}
vec{p} &= m ~ vec{v} \
end{align*}
$$
Since the momentum is depending on the mass and the velocity. Solve for all particles in the system at rest:
$$
begin{align*}
vec{p} &= m ~ vec{v} \
&= m times 0 mathrm{~m/s} \
&= 0 mathrm{~kg cdot m/s}
end{align*}
$$
So, if the velocity of the particle is zero, then the momentum of the system is equal to zero. Therefore, if the kinetic energy of the system is zero, then the momentum of the system is equal to zero.
In order to evaluate the kinetic energy of a particle, we use the following relation:
$$
begin{align*}
K.E &= dfrac{1}{2} ~ m ~ v^{2} \
end{align*}
$$
As we know the kinetic energy is a scalar depends only on the magnitude. As the textbook mentions that the momentum of the system is given by the mass times the velocity.
$$
begin{align*}
vec{p} &= m ~ vec{v} \
end{align*}
$$
Since the momentum is depending on the mass and the velocity.
$$
begin{align*}
vec{p} &= m ~ vec{v} \
end{align*}
$$
Since the momentum is a vector, then it’s depending on the magnitude and the direction. So, it is possible that each particle in the system has the same magnitude of momentum and opposite direction of motion, then the momentum vectors cancel each other. Therefore, the total momentum of the system is equal to zero. So, the system that has a kinetic energy of $10000 mathrm{~J}$ can easily have a total momentum of zero.
As the textbook mentions that the momentum of the system is given by the mass times the velocity.
$$
begin{align*}
vec{p} &= m ~ vec{v} \
end{align*}
$$
So, the momentum is equal to the velocity multiplied by the mass. So, the direction of the momentum and the velocity is the same. As we know the conservation law of momentum assigns that the total momentum of the system is equal to zero. So, the momentum is a conserved quantity while the velocity isn’t conserved.
textbf{Concept:}
$$
Product of mass and speed of each object will give momentum for each case and the result can then be compared
$textbf{Solution:}$
$$
p_A=m_A v_A = (1kg)(1m/s)=1kg.m/s
$$
$$
p_B=m_B v_B = (2kg)(3m/s)=6kg.m/s
$$
$$
p_C=m_C v_C = (0.1kg)(20m/s)=2kg.m/s
$$
$$
p_D=m_D v_D = (5kg)(0.2m/s)=1kg.m/s
$$
Then comparing gives the ranking
$$
boxed{bf color{#4257b2}p_A=p_D<p_C<p_B}
$$
p_A=p_D<p_C<p_B
$$
textbf{Concept:}
$$
Masses are calculated by dividing the momentum with the velocity of the respective object
$textbf{Solution:}$
$$
m_A=p_A/v_A=(4kg,m/s)(1/s)
$$
$$
m_B=p_B/v_B=(5kg,m/s)(2/s)
$$
$$
m_C=p_C/v_C=(1kg,m/s)(4/s)
$$
$$
m_D=p_D/v_D=(2kg,m/s)(0.5/s)
$$
Comparing the masses gives the ranking
$$
boxed{bf color{#4257b2}m_C<m_B<m_A=m_D}
$$
m_C<m_B<m_A=m_D
$$
The mass of the baseball is $m = 0.15 mathrm{~kg}$. The baseball momentum is $p = 0.78 mathrm{~kg cdot m/s}$.
$textbf{Required: }$
Finding the speed before the landing.
As the textbook mentions that the momentum of the baseball is given by the mass times the velocity.
$$
begin{align*}
vec{p} &= m ~ vec{v} \
end{align*}
$$
Rearrange and solve for the speed before the landing:
$$
begin{align*}
vec{v} &= dfrac{ vec{p} }{ m} \
&= dfrac{ 0.78 mathrm{~kg cdot m/s} }{ 0.15 mathrm{~kg} } \
&= 5.2 mathrm{~m/s}
end{align*}
$$
So, the speed of the ball just before landing is $5.2 mathrm{~m/s}$.
The speed of the moving car is $v = 25 mathrm{~kg}$. The car’s momentum is $p = 3.2 times 10^{4} mathrm{~kg cdot m/s}$.
$textbf{Required: }$
Finding the mass of the car.
As the textbook mentions that the momentum of the baseball is given by the mass times the velocity.
$$
begin{align*}
vec{p} &= m ~ vec{v} \
end{align*}
$$
Rearrange and solve for the mass of the car:
$$
begin{align*}
m &= dfrac{ vec{p} }{vec{v}} \
&= dfrac{ 3.2 times 10^{4} mathrm{~kg cdot m/s} }{ 25 mathrm{~m/s} } \
&= 1280 mathrm{~kg}
end{align*}
$$
So, the mass of the car is $1280 mathrm{~kg}$.
The salmon’s mass is $m = 5.2 mathrm{~kg}$. The speed of the salmon is $v = 2.3 mathrm{~m/s}$.
$textbf{Required: }$
Finding the salmon’s momentum.
As the textbook mentions that the momentum of the baseball is given by the mass times the velocity.
$$
begin{align*}
vec{p} &= m ~ vec{v} \
&= 5.2 mathrm{~kg} times 2.3 mathrm{~m/s} \
&= 11.96 mathrm{~kg cdot m/s}
end{align*}
$$
So, the salmon’s momentum is $11.96 mathrm{~kg cdot m/s}$.
The mass of the first player is $m_{1} = 45 mathrm{~kg}$. The speed of the first player is $v_{1} = 1.4 mathrm{~m/s}$ to the right. The mass of the second player is $m_{2} = 32 mathrm{~kg}$. The speed of the second player is $v_{2} = 2.1 mathrm{~m/s}$ to the left.
$textbf{Required: }$
Finding the magnitude of the total momentum.
As the textbook mentions that the momentum of the baseball is given by the mass times the velocity.
$$
begin{align*}
vec{p} &= m ~ vec{v} \
end{align*}
$$
According to superposition principle, the total momentum of the system is given by
$$
begin{align*}
vec{p_{total}} &= vec{p_{1}} + vec{p_{2}} \
&= m_{1} ~ vec{v_{1}} + m_{2} ~ vec{v_{2}} \
&= left( 45 mathrm{~kg} times 1.4 mathrm{~m/s} right) ~ hat{e} – left( 32 mathrm{~kg} times 2.1 mathrm{~m/s} right) ~ hat{e} \
&= – 4.2 mathrm{~kg cdot m/s} ~ hat{e}
end{align*}
$$
So, the magnitude of the total momentum is $4.2 mathrm{~kg cdot m/s}$ to the left.
The mass of the first player is $m_{1} = 47 mathrm{~kg}$. The speed of the first player is $v_{1} = 1.1 mathrm{~m/s}$ to the right. The mass of the second player is $m_{2} = 38 mathrm{~kg}$. The total momentum of the two players is $p = 2.2 mathrm{~kg cdot m/s}$ to the left.
$textbf{Required: }$
Finding the speed and the direction of motion of second player.
As the textbook mentions that the momentum of the player is given by the mass times the velocity.
$$
begin{align*}
vec{p} &= m ~ vec{v} \
end{align*}
$$
According to superposition principle, the total momentum of the system is given by
$$
begin{align*}
vec{p_{total}} &= vec{p_{1}} + vec{p_{2}} \
&= m_{1} ~ vec{v_{1}} + m_{2} ~ vec{v_{2}} \
&= left( 45 mathrm{~kg} times 1.4 mathrm{~m/s} right) ~ hat{e} – left( 32 mathrm{~kg} times 2.1 mathrm{~m/s} right) ~ hat{e} \
&= – 4.2 mathrm{~kg cdot m/s} ~ hat{e}
end{align*}
$$
Rearrange and solve for the velocity of the second player:
$$
begin{align*}
vec{v_{2}} &= dfrac{vec{p_{total}} – m_{1} ~ vec{v_{1}} }{ m_{2} } \
&= dfrac{- 2.2 mathrm{~kg cdot m/s} ~ hat{e} – left( 47 mathrm{~kg} times 1.1 mathrm{~m/s} right) ~ hat{e} }{ 38 mathrm{~kg} } \
&= -1.418 mathrm{~m/s} ~ hat{e}
end{align*}
$$
So, the speed of the second player is $1.418 mathrm{~m/s}$ and the second player moves to the left.
The mass of the first cart is $m_{1} = 0.35 mathrm{~kg}$. The speed of the first cart is $v_{1} = 1.2 mathrm{~m/s}$. The mass of the second cart is $m_{2} = 0.61 mathrm{~kg}$. The total momentum of the system is $p = 0 mathrm{~kg cdot m/s}$ to the left.
$textbf{Required: }$
Finding the speed of second cart.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
end{align*}
$$
According to conservation law of momentum, the impulse is equal to zero.
$$
begin{align*}
Delta p_{t} &= Delta p_{1} + Delta p_{2} \
&= 0 \
&= m_{1} ~ vec{v_{1}} + m_{2} ~ vec{v_{2}} \
end{align*}
$$
Rearrange and solve for the mass of the hokey player:
$$
begin{align*}
v_{2} &= – dfrac{ m_{1} ~ v_{1} }{ m_{2} } \
&= – dfrac{ 0.35 mathrm{~kg} times 1.2 mathrm{~m/s} }{ 0.61 mathrm{~kg} } \
&= – 0.689 mathrm{~m/s}
end{align*}
$$
So, the speed of the second cart is $0.689 mathrm{~m/s}$ in the opposite direction of the first cart motion.
The mass of the ball is $m = 0.28 mathrm{~kg}$. The initial speed of the ball is $v_{i} = 2.5 mathrm{~m/s}$ directed downward. The final speed of the ball is $v_{f} = 2 mathrm{~m/s}$ directed upward.
$textbf{Required: }$
(a) Finding the momentum of the ball before it hit the floor.
(b) Finding the changing in momentum of the ball during its impact with the floor.
Let the downward direction is the positive direction. As the textbook mentions that the initial momentum of the ball is given by the mass times the velocity.
$$
begin{align*}
vec{p} &= m ~ vec{v} \
&= 0.28 mathrm{~kg} times 2.5 mathrm{~m/s} ~ hat{e}\
&= 0.7 mathrm{~kg cdot m/s} ~ hat{e}\
end{align*}
$$
So, the initial momentum of the ball before it hit the floor is $0.7 mathrm{~kg cdot m/s}$ directed downward.
As the textbook mentions that the momentum of the baseball is given by the mass times the velocity.
$$
begin{align*}
vec{p} &= m ~ vec{v} \
end{align*}
$$
In order to evaluate the changing in momentum of the ball, we use the following relation:
$$
begin{align*}
Delta vec{p} &= vec{p_{f}} – vec{p_{i}} \
&= m ~ vec{v_{f}} – m ~ vec{v_{i}} \
&= left( 0.28 mathrm{~kg} times 2.5 mathrm{~m/s} right) ~ hat{e} – left( – 0.28 mathrm{~kg} times 2 mathrm{~m/s} right) ~ hat{e} \
&= 1.2 mathrm{~kg cdot m/s} ~ hat{e}
end{align*}
$$
So, the changing in the momentum of the ball is $1.2 mathrm{~kg cdot m/s}$ in the downard direction.
(b) The changing in the momentum of the ball is $1.2 mathrm{~kg cdot m/s}$ in the downard direction.
The mass of the dog is $m_{dog} = 26 mathrm{~kg}$. The velocity of the dog is $v_{dog} = 2.7 mathrm{~m/s}$ which is directed northward. The mass of the cat is $m_{cat} = 5.3 mathrm{~kg}$. The velocity of the cat is $v_{cat} = 3 mathrm{~m/s}$ which is directed eastward.
$textbf{Required: }$
Finding the magnitude and the direction of the system’s total momentum.
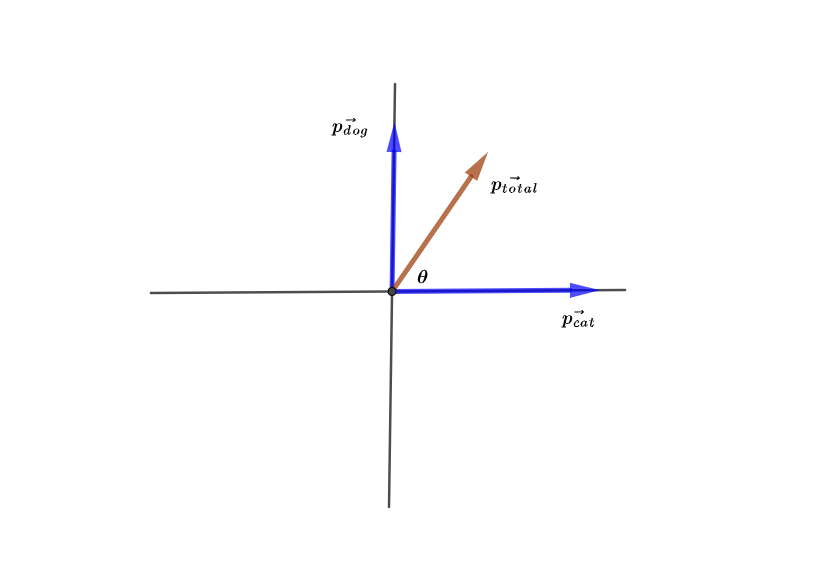
Solve for the dog:
As the textbook mentions that the initial momentum of the dog is given by the mass times the velocity.
$$
begin{align*}
vec{p_{dog}} &= m_{dog} ~ vec{v_{dog}} \
&= 26 mathrm{~kg} times 2.7 mathrm{~m/s} ~ hat{y}\
&= 70.2 mathrm{~kg cdot m/s} ~ hat{y}\
end{align*}
$$
Solve for the cat:
As the textbook mentions that the initial momentum of the dog is given by the mass times the velocity.
$$
begin{align*}
vec{p_{cat}} &= m_{cat} ~ vec{v_{cat}} \
&= 5.3 mathrm{~kg} times 3 mathrm{~m/s} ~ hat{x}\
&= 15.9 mathrm{~kg cdot m/s} ~ hat{x}\
end{align*}
$$
In order to evaluate the magnitude of the total momentum, we use the following relation:
$$
begin{align*}
p_{total} &= sqrt{ p_{cat}^{2} + p_{dog}^{2} } \
&= sqrt{ left( 15.9 mathrm{~kg cdot m/s} right)^{2} + left( 70.2 mathrm{~kg cdot m/s} right)^{2} } \
&= 71.978 mathrm{~kg cdot m/s}
end{align*}
$$
In order to evaluate the direction of the total momentum of the system, we use the following relation:
$$
begin{align*}
tan left( theta right) &= dfrac{ p_{dog} }{ p_{cat} } \
theta &= tan^{-1} left( dfrac{ p_{dog} }{ p_{cat} } right) \
&= tan^{-1} left( dfrac{ 70.2 mathrm{~kg cdot m/s} }{ 15.9 mathrm{~kg cdot m/s} } right) \
&= 77.238^{circ}
end{align*}
$$
So, the magnitude of the total momentum of the system is $71.978 mathrm{~kg cdot m/s}$ and its direction is $77.238^{circ}$ to the north of east.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
So, the force is equal to the rate of the change in momentum within a desire time interval. As we see in the previous theorem, the impulse is directly proportional to the force. If the impulse increases, then the force will increase. So, the force is equal to the rate of the change in momentum within a desire time interval.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
So, the force is equal to the rate of the change in momentum within a desire time interval. As we see in the previous theorem, the impulse is directly proportional to the force. If the impulse increases, then the force will increase. So, the force is equal to the rate of the change in momentum within a desire time interval. So, the answer is “No, it isn’t possible for a small force to deliver a greater impulse than a large force.”
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
In this problem, we deal with the time. The time interval affects the force but the change in momentum and the impulse stays the same. So, the school bus faces a change in momentum that was equal to the amount of change in momentum due to velocity rapidly slow down. So, the answer is “The magnitude of the impulse, in this case, is equal to the magnitude of the impulse with the gradual stop.”
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
So, the force is equal to the rate of the change in momentum within a desire time interval. As we see in the previous theorem, the impulse is directly proportional to the force. In this problem, we deal with time. The time interval affects the force but the change in momentum and the impulse stays the same. So, the airbags used to elongate the time interval of the collision, then the exerted force by the car on the head of the vehicle’s occupants will be decreased.
The magnitude of the net force is $F_{1} = 200 mathrm{~N}$. The mass of the boulder is $m_{1} = 100 mathrm{~kg}$. The force that exerted on the pebble is $F_{2} = 0.1 mathrm{~kg}$. The mass of the pebble is $m_{2} = 0.1 mathrm{~kg}$. The time interval is $Delta t = 1 mathrm{~s}$.
Solve for the boulder’s case:
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I_{1}} &= vec{F_{1}} ~ Delta t_{1} \
&= Delta vec{p_{1}} \
&= 200 mathrm{~N} times 1 mathrm{~s} \
&= 200 mathrm{~kg cdot m/s}
end{align*}
$$
Solve for the pebble’s case:
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I_{2}} &= vec{F_{2}} ~ Delta t_{2} \
&= Delta vec{p_{2}} \
&= 200 mathrm{~N} times 1 mathrm{~s} \
&= 200 mathrm{~kg cdot m/s}
end{align*}
$$
So, the change in the boulder’s momentum in $1 mathrm{~s}$ equals to the change in the pebble’s momentum in the same time interval.
The answer is “C. Equal force means an equal change in momentum for a given time period.”
(b) C. Equal force means an equal change in momentum for a given time period.
The magnitude of the net force is $F_{1} = 200 mathrm{~N}$. The mass of the boulder is $m_{1} = 100 mathrm{~kg}$. The force that exerted on the pebble is $F_{2} = 0.1 mathrm{~kg}$. The mass of the pebble is $m_{2} = 0.1 mathrm{~kg}$. The time interval is $Delta t = 1 mathrm{~s}$.
Solve for the boulder’s case:
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I_{1}} &= vec{F_{1}} ~ Delta t_{1} \
&= Delta vec{p_{1}} \
&= vec{p_{f}} – vec{p_{i}} \
&= 200 mathrm{~N} times 1 mathrm{~s} \
&= 200 mathrm{~kg cdot m/s}
end{align*}
$$
Solve for the pebble’s case:
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I_{2}} &= vec{F_{2}} ~ Delta t_{2} \
&= Delta vec{p_{2}} \
&= 200 mathrm{~N} times 1 mathrm{~s} \
&= 200 mathrm{~kg cdot m/s}
end{align*}
$$
So, the change in the boulder’s momentum in $1 mathrm{~s}$ equals to the change in the pebble’s momentum in the same time interval. But the rate of change of the heavier object is less than the rate of change of the lighter object with the same affecting force, changing in momentum, and impulse. So, the answer is “the change in the boulder’s
speed in 1 s less than the change in the speed of the pebble in the same time interval.”
The choice (A) is correct. So, the answer is “The larger mass of the boulder results in a smaller acceleration.”
(b) The larger mass of the boulder results in a smaller acceleration.
Multiply the force with duration to calculate the impulse and then rank them.
$$
textbf{Solution:}
$$
$$
I_{A}=F_{A}Delta t_{A}=(1N)(1s)=1kg.m/s
$$
$$
I_{B}=F_{B}Delta t_{B}=(2N)(0.3s)=0.6kg.m/s
$$
$$
I_{C}=F_{C}Delta t_{C}=(5N)(0.1s)=0.5kg.m/s
$$
$$
I_{D}=F_{D}Delta t_{D}=(10N)(0.07s)=0.7kg.m/s
$$
Now compare the impulse to rank them
$$
bf color{#4257b2} boxed{I_C<I_B<I_D<I_A}
$$
I_C < I_B < I_D <I_A
$$
The mass of the baseball is $m = 0.14 mathrm{~kg}$. The initial speed of the baseball is $v_{i} = 0 mathrm{~m/s}$. The changing in momentum (impulse) is $Delta p = 0.78 mathrm{~kg cdot m/s}$.
$textbf{Required: }$
Finding the time interval that the ball takes in the air.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
Rearrange and solve for the time interval that the ball takes in the air:
$$
begin{align*}
Delta t &= dfrac{ vec{I} }{ vec{F} } \
&= dfrac{ Delta vec{p} }{ vec{F} } \
&= dfrac{ Delta vec{p} }{ vec{W} } \
&= dfrac{ Delta p }{ m ~ g } \
&= dfrac{0.78 mathrm{~kg cdot m/s} }{ 0.14 mathrm{~kg} times 9.8 mathrm{~m/s^{2}} } \
&= 0.569 mathrm{~s}
end{align*}
$$
So, the time interval that the ball takes in the air is $0.569 mathrm{~s}$.
The magnitude of the force that the player exerted on the ball is $F = 1250 mathrm{~N}$. The time interval of the kicking is $Delta t = 5.95 times 10^{-3} mathrm{~s}$.
$textbf{Required: }$
Finding the magnitude if the impulse.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
I &= F ~ Delta t \
&= Delta p \
&= 1250 mathrm{~m/s} times 5.95 times 10^{-3} mathrm{~s} \
&= 7.438 mathrm{~kg cdot m/s}
end{align*}
$$
So, the magnitude of the impulse is $7.438 mathrm{~kg cdot m/s}$.
The time interval that the ball was in contact with the club is $Delta t = 1 times 10^{-3} mathrm{~s}$. The mass of the ball is $m = 0.045 mathrm{~kg}$. The speed of the ball is $v_{f} = 67 mathrm{~m/s}$.
$textbf{Required: }$
Finding the magnitude of the exerted force on the ball by the club.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
Rearrange and solve for the magnitude of the exerted force on the ball by the club:
$$
begin{align*}
vec{F} &= dfrac{ vec{I} }{ Delta t } \
&= dfrac{ m ~ left( vec{v_{f}} – vec{v_{i}} right) }{ Delta t } \
&= dfrac{ 0.045 mathrm{~kg} times left( 67 mathrm{~m/s} – 0 mathrm{~m/s} right) }{ 1 times 10^{-3} mathrm{~s} } \
&= 3.015 times 10^{3} mathrm{~N}
end{align*}
$$
So, the magnitude of the exerted force on the ball by the club is $3.015 times 10^{3} mathrm{~N}$.
The mass of the ball is $m = 0.52 mathrm{~kg}$. The initial speed of the ball is $v_{i} = 0 mathrm{~m/s}$. The average exerted force is $F = 190 mathrm{~N}$. The time interval of the collision is $Delta t = 7.2 times 10^{-3} mathrm{~s}$.
$textbf{Required: }$
Finding the final speed of the ball after it is hit.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
Rearrange and solve for thefinal speed of the ball after it is hit:
$$
begin{align*}
v_{f} &= dfrac{ vec{F} ~ Delta t + m ~ v_{i} }{ m } \
&= dfrac{ 190 mathrm{~N} times 7.2 times 10^{-3} mathrm{~s} +0.52 mathrm{~kg} times 0 mathrm{~m/s} }{ 0.52 mathrm{~kg} } \
&= 2.631 mathrm{~m/s}
end{align*}
$$
So, the final speed of the ball is $2.631 mathrm{~m/s}$.
The mass of the bullet is $m = 5.5 times 10^{-3} mathrm{~kg}$. The initial speed of the bullet is $v_{i} = 325 mathrm{~m/s}$. The final speed of the bullet is $v_{f} = 0 mathrm{~m/s}$. The average force that exerted on the bullet is $F = 550 mathrm{~N}$.
$textbf{Required: }$
Finding the time interval that the bullet takes to come to rest.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
Rearrange and solve for the time interval that the bullet takes to stop:
$$
begin{align*}
Delta t &= dfrac{ vec{I} }{ vec{F} } \
&= dfrac{ Delta vec{p} }{ vec{F} } \
&= dfrac{ m ~ left( vec{v_{f}} – vec{v_{i}} right) }{ vec{F} } \
&= dfrac{ 5.5 times 10^{-3} mathrm{~kg} times left( 0 mathrm{~m/s} – left( – 325 mathrm{~m/s} right) right) }{ 550 mathrm{~N} } \
&= 3.25 times 10^{-3} mathrm{~s}
end{align*}
$$
So, the time interval that the bullet to stop is $3.25 times 10^{-3} mathrm{~s}$.
The initial speed of the volleyball is $v_{i} = 4.2 mathrm{~m/s}$. The final speed of the volleyball is $v_{f} = – 24 mathrm{~m/s}$. The impulse that delivered to the ball by the player is $I = – 9.3 mathrm{~kg cdot m/s}$.
$textbf{Required: }$
Finding the mass of the volleyball.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
Rearrange and solve for the mass of the volleyball:
$$
begin{align*}
m &= dfrac{ vec{I} }{ left( vec{v_{f}} – vec{v_{i}} right) } \
&= dfrac{ – 9.3 mathrm{~kg cdot m/s} }{ left( – 24 mathrm{~m/s} – 4.2 mathrm{~m/s} right) } \
&= 0.3298 mathrm{~kg}
end{align*}
$$
So, the mass of the volleyball is $0.3298 mathrm{~kg}$.
textbf{Concept}\
We will use velocity-position equation to calculate the initial speed of with which it hits the floor and the height of rebound and impulse-momentum equation to find the impulse delivered to the floor. Assume upward be positive direction and hitting speed be $-v_i$ and rebound speed be $v_f$\
textbf{Solution:}
Finding $v_i$ with velocity position equation\
$$v^2_{i}=v^2_{o}-2gDelta y$$
$$v_{i}=sqrt{v^2_{o}-2gDelta y}=sqrt{0^2-2(9.81m/s^2)(-1.4m)}=-5.24m/s$$
$$v_{i}=-5.24m/s$$
Finding $v$ with velocity position equation again\
$$v^2=v^2_{f}-2gDelta y$$
$$v_{f}=sqrt{v^2_{f}-2gDelta y}=sqrt{0^2-2(9.81m/s^2)(0.64m)}=3.54m/s$$
$$v_{f}=3.54m/s$$
From above two result we find the impulse\
$$I=mDelta v=m(v_f-v_i)$$
$$bf color{blue} boxed{I=(0.015kg)(-8.78)=-0.13kg.m/s}mbox{(upward)}$$\\
b.)
To rebound higher, the speed of marble need to be higher and impulse would have been bf color{blue} boxed{mbox{greater then}} the impulse calculated in part(a)\
As the textbook mentions that the momentum of the object is given by the mass times the velocity.
$$
begin{align*}
vec{p} &= m ~ vec{v} \
end{align*}
$$
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
Rearrange and solve for the force:
$$
begin{align*}
vec{F} &= dfrac{ vec{I} }{ Delta t } \
&= dfrac{ Delta vec{p} }{ Delta t } \
&= dfrac{ dp }{ dt} \
end{align*}
$$
As we know the internal force generates the system momentum. As we see in the previous calculations, the external force is equal to the change in momentum with respect to time. So, the external force can change the total momentum of the system.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
According to conservation law of momentum, the impulse is equal to zero.
$$
begin{align*}
Delta p_{t} &= Delta p_{1} + Delta p_{2} \
&= 0 \
&= m_{1} ~ left( vec{v_{f,1}} – vec{v_{i,1}} right) + m_{2} ~ left( vec{v_{f,2}} – vec{v_{i,2}} right) \
end{align*}
$$
Since the total momentum of the system is equal to zero. So, the momentum of each object in the system can change but the arithmetic sum of the changes in the momentum of the two objects should be equals to zero. For example, if the change in the momentum of the first object increases by $5 mathrm{~kg cdot m/s}$, then the change in the momentum of the second object will decrease by $5 mathrm{~kg cdot m/s}$.
Let the mass of the first object is $m_{1} = 0.5 mathrm{~kg}$, the mass of the second object is $m_{2} = 1 mathrm{~kg}$, the initial velocity of the first object is $v_{i,1} = -3 mathrm{~m/s}$, the initial velocity of the second object is $v_{i,2} = 2 mathrm{~m/s}$, the final velocity of the first object is $v_{f,1} = – 1.5 mathrm{~m/s}$, and the final speed of the second object is $v_{f,2} = 1.25 mathrm{~m/s}$.
As the textbook mentions that the momentum of the system is given by the mass times the velocity.
$$
begin{align*}
vec{p} &= m ~ vec{v} \
end{align*}
$$
So, the momentum is equal to the velocity multiplied by the mass. So, the direction of the momentum and the velocity are the same. As we know the conservation law of momentum assigns that the total momentum of the system is equal to zero. So, the momentum is a conserved quantity while the velocity isn’t conserved.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
According to superposition of momentum:
$$
begin{align*}
Delta p_{t} &= Delta p_{1} + Delta p_{2} \
&= m_{1} ~ left( vec{v_{f,1}} – vec{v_{i,1}} right) + m_{2} ~ left( vec{v_{f,2}} – vec{v_{i,2}} right) \
&= 0.5 mathrm{~kg} times left( – 1.5 mathrm{~m/s} – left( – 3 mathrm{~m/s} right) right) + 1 mathrm{~kg} times left( 1.25 mathrm{~m/s} – 2 mathrm{~m/s} right) \
&= 0 mathrm{~kg cdot m/s}
end{align*}
$$
In order to evaluate the total initial velocity, we use the following relation:
$$
begin{align*}
v_{i,t} &= v_{i,1} + v_{i,2} \
&= -3 mathrm{~m/s} + 2 mathrm{~m/s} \
&= – 1 mathrm{~m/s}
end{align*}
$$
In order to evaluate the total final velocity, we use the following relation:
$$
begin{align*}
v_{f,t} &= v_{f,1} + v_{f,2} \
&= – 1.5 mathrm{~m/s} + 1.25 mathrm{~m/s} \
&= – 0.25 mathrm{~m/s}
end{align*}
$$
So, the total initial velocity before the collision isn’t equal to the total final velocity after the collision.
So, the momentum is conservative while the velocity isn’t conservative.
So, the momentum is conservative while the velocity isn’t conservative.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
According to conservation law of momentum, the impulse is equal to zero.
$$
begin{align*}
Delta p_{t} &= Delta p_{1} + Delta p_{2} \
&= 0 \
end{align*}
$$
So, the larger backward momentum of the burning particles is equal to the forward momentum of the rocket. So, the total momentum of the system remains constant. According to Newton’s third law:
$$
begin{align*}
F_{1,2} &= – F_{2,1} \
end{align*}
$$
So, the rocket moves due to the repulsion force exerted by the particles on the rocket. So, in any case, the rocket moves forward without needing any exhaust gases to push against.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
According to conservation law of momentum, the impulse is equal to zero.
$$
begin{align*}
Delta p_{t} &= Delta p_{1} + Delta p_{2} \
&= 0 \
end{align*}
$$
So, the astronaut can propel himself by throwing the wrench from the back to the forward away from the space shuttle. So, the forward momentum will create and the total momentum of the system should remain constant. Therefore, the system creates momentum in the backward direction. According to Newton’s third law:
$$
begin{align*}
F_{1,2} &= – F_{2,1} \
end{align*}
$$
So, the astronaut moves due to the repulsion force exerted by the system that makes him move close to the space shuttle.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
According to conservation law of momentum, the impulse is equal to zero.
$$
begin{align*}
Delta p_{t} &= Delta p_{1} + Delta p_{2} \
&= 0 \
Delta p_{1} &= – Delta p_{2} \
end{align*}
$$
So, the bullet and the gun have an equal magnitude of momentum and opposite directions. But the rate of change of velocity of the heavier object is less than the rate of change of velocity of the lighter object with the same affecting force, changing in momentum, and impulse.
In order to evaluate the kinetic energy, we use the following relation:
$$
begin{align*}
K.E &= dfrac{1}{2} ~ m ~ v^{2}
end{align*}
$$
So, the bullet that has a small mass and large velocity have greater kinetic energy than the gun that has greater mass and less velocity. So, the damage caused by the bullet is due to the large kinetic energy over a small area.
The mass of the first ice skater is $m_{1} = 45 mathrm{~kg}$. The initial speed of the two ice skaters is $v_{i} = 0 mathrm{~m/s}$. The final speed of first skater is $v_{f,1} = 0.62 mathrm{~m/s}$. The final speed of second skater is $v_{f,2} = 0.89 mathrm{~m/s}$.
$textbf{Required: }$
Finding the mass of the second skater.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
According to conservation law of momentum, the impulse is equal to zero.
$$
begin{align*}
Delta p_{t} &= Delta p_{1} + Delta p_{2} \
&= 0 \
&= m_{1} ~ left( vec{v_{f,1}} – vec{v_{i,1}} right) + m_{2} ~ left( vec{v_{f,2}} – vec{v_{i,2}} right) \
&= m_{1} ~ left( vec{v_{f,1}} – 0right) + m_{2} ~ left( vec{v_{f,2}} – 0 right) \
end{align*}
$$
Rearrange and solve for the mass of the second skater:
$$
begin{align*}
m_{2} &= – dfrac{ m_{1} ~ v_{f,1} }{ v_{f,2} } \
&= – dfrac{ 45 mathrm{~kg} times 0.62 mathrm{~m/s} }{- 0.89 mathrm{~m/s} } \
&= 31.348 mathrm{~kg}
end{align*}
$$
So, the mass of the second skater is $31.348 mathrm{~kg}$.
The initial speed of the two rollerblades is $v_{i} = 0 mathrm{~m/s}$. The mass of Tracey is $m_{1} = 32 mathrm{~kg}$. The mass of Jonas is $m_{2} = 45 mathrm{~kg}$. The final speed of Jonas is $v_{f,2} = 0.55 mathrm{~m/s}$.
$textbf{Required: }$
Finding the final speed of Tracey.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
According to conservation law of momentum, the impulse is equal to zero.
$$
begin{align*}
Delta p_{t} &= Delta p_{1} + Delta p_{2} \
&= 0 \
&= m_{1} ~ left( vec{v_{f,1}} – vec{v_{i,1}} right) + m_{2} ~ left( vec{v_{f,2}} – vec{v_{i,2}} right) \
&= m_{1} ~ left( vec{v_{f,1}} – 0right) + m_{2} ~ left( vec{v_{f,2}} – 0 right) \
end{align*}
$$
Rearrange and solve for the final speed of Tracey:
$$
begin{align*}
v_{f,1} &= – dfrac{ m_{2} ~ v_{f,2} }{ m_{1} } \
&= – dfrac{ 45 mathrm{~kg} times 0.55 mathrm{~m/s} }{ 32 mathrm{~kg}} \
&= – 0.773 mathrm{~m/s}
end{align*}
$$
So, the mass of the final speed of Tracey is $0.773 mathrm{~m/s}$.
The mass of astronaut is $m_{1} = 92 mathrm{~kg}$. The mass of satellite is $m_{2} = 1.2 times 10^{3} mathrm{~kg}$. The initial speed of astronaut and the satellite is zero. The final speed of the satellite is $v_{f,2} = 0.14 mathrm{~m/s}$ directed away from the station. Thee time interval that the astronaut takes to contact with the station is $Delta t = 7.5 mathrm{~s}$.
$textbf{Required: }$
Finding the initial distance from the station to the astronaut.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
end{align*}
$$
According to conservation law of momentum, the impulse is equal to zero.
$$
begin{align*}
Delta p_{t} &= Delta p_{1} + Delta p_{2} \
&= 0 \
&= m_{1} ~ left( vec{v_{f,1}} – vec{v_{i,1}} right) + m_{2} ~ left( vec{v_{f,2}} – vec{v_{i,2}} right) \
&= m_{1} ~ left( vec{v_{f,1}} – 0right) + m_{2} ~ left( vec{v_{f,2}} – 0 right) \
end{align*}
$$
Rearrange and solve for the final speed of the astronaut:
$$
begin{align*}
v_{f,1} &= – dfrac{ m_{2} ~ v_{f,2} }{ m_{1} } \
&= – dfrac{ 1.2 times 10^{3} mathrm{~kg} times 0.14 mathrm{~m/s} }{ 92 mathrm{~kg} } \
&= 1.826 mathrm{~m/s}
end{align*}
$$
In order to evaluate the speed of the astronaut, we use the following relation:
$$
begin{align*}
v_{f,1} &= dfrac{ d }{ Delta t } \
d &= v_{f,1} ~ Delta t \
&= 1.826 mathrm{~m/s} times 7.5 mathrm{~s} \
&= 13.695 mathrm{~m/s}
end{align*}
$$
So, the initial distance from the station to the astronaut is $13.695 mathrm{~m/s}$.
The mass of the lumberjack is $m_{1} = 85 mathrm{~kg}$. The mass of the floating log is $m_{2} = 380 mathrm{~kg}$. The initial speed of both the lumberjack and the floating log is equal to zero.
$textbf{Required: }$
(a) Finding the relative speed of the log to the shore, if the relative speed of the lumberjack is $2.7 mathrm{~m/s}$.
(b) Finding if the relative speed to the shore be greater than, less than, or the same as in part (a) if the log’s mass were greater.
(c) Finding if the relative speed to the shore, if the log’s mass is $m_{2} = 450 mathrm{~kg}$.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
According to conservation law of momentum, the impulse is equal to zero.
$$
begin{align*}
Delta p_{t} &= Delta p_{1} + Delta p_{2} \
&= 0 \
&= m_{1} ~ left( vec{v_{f,1}} – vec{v_{i,1}} right) + m_{2} ~ left( vec{v_{f,2}} – vec{v_{i,2}} right) \
&= m_{1} ~ left( vec{v_{f,1}} – 0right) + m_{2} ~ left( vec{v_{f,2}} – 0 right) \
end{align*}
$$
Rearrange and solve for the relative speed of the log to the shore:
$$
begin{align*}
v_{2} &= – dfrac{ m_{1} ~ v_{f,1} }{ m_{2} } \
&= – dfrac{ 85 mathrm{~kg} times 2.7 mathrm{~m/s} }{ 380 mathrm{~m/s} } \
&= – 0.604 mathrm{~m/s}
end{align*}
$$
So, the relative speed of the log to the shore is $0.604 mathrm{~m/s}$ in the opposite direction of the lumberjack’s speed.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
According to conservation law of momentum, the impulse is equal to zero.
$$
begin{align*}
Delta p_{t} &= Delta p_{1} + Delta p_{2} \
&= 0 \
&= m_{1} ~ left( vec{v_{f,1}} – vec{v_{i,1}} right) + m_{2} ~ left( vec{v_{f,2}} – vec{v_{i,2}} right) \
&= m_{1} ~ left( vec{v_{f,1}} – 0right) + m_{2} ~ left( vec{v_{f,2}} – 0 right) \
end{align*}
$$
Rearrange and solve for the relative speed of the log to the shore:
$$
begin{align*}
v_{2} &= – dfrac{ m_{1} ~ v_{f,1} }{ m_{2} } \
end{align*}
$$
So, the relative speed to the shore is inversely proportional to the log’s mass. Therefore, if the log’s mass increases, then the relative speed to the shore in this case is less than the relative speed to the shore in part (a).
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
According to conservation law of momentum, the impulse is equal to zero.
$$
begin{align*}
Delta p_{t} &= Delta p_{1} + Delta p_{2} \
&= 0 \
&= m_{1} ~ left( vec{v_{f,1}} – vec{v_{i,1}} right) + m_{2} ~ left( vec{v_{f,2}} – vec{v_{i,2}} right) \
&= m_{1} ~ left( vec{v_{f,1}} – 0right) + m_{2} ~ left( vec{v_{f,2}} – 0 right) \
end{align*}
$$
Rearrange and solve for the relative speed of the log to the shore:
$$
begin{align*}
v_{2} &= – dfrac{ m_{1} ~ v_{f,1} }{ m_{2} } \
&= – dfrac{ 85 mathrm{~kg} times 2.7 mathrm{~m/s} }{ 450 mathrm{~m/s} } \
&= – 0.51 mathrm{~m/s}
end{align*}
$$
So, the relative speed of the log to the shore is $0.51 mathrm{~m/s}$ in the opposite direction of the lumberjack’s speed.
(b) If the log’s mass increases, then the relative speed to the shore, in this case, is less than the relative speed to the shore in part (a).
(c) The relative speed of the log to the shore is $0.51 mathrm{~m/s}$ in the opposite direction of the lumberjack’s speed.
As we know in the elastic collision, the momentum and the kinetic energy are conservative. But in the inelastic collision, the momentum and the kinetic energy are non-conservative. Therefore, the completely inelastic collision from other inelastic collisions is kinetic energy is not conserved, and the colliding objects stick together after the collision.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
Rearrange and solve for the force:
$$
begin{align*}
vec{F} &= dfrac{ vec{I} }{ Delta t } \
&= dfrac{ Delta vec{p} }{ Delta t } \
&= dfrac{ dp }{ dt} \
end{align*}
$$
As we know the internal force generates the system momentum. As we see in the previous calculations, the external force is equal to the change in momentum with respect to time. So, the external force can change the total momentum of the system.
According to conservation law of momentum, the impulse is equal to zero.
$$
begin{align*}
Delta p_{t} &= Delta p_{1} + Delta p_{2} \
&= 0 \
&= m_{1} ~ left( vec{v_{f,1}} – vec{v_{i,1}} right) + m_{2} ~ left( vec{v_{f,2}} – vec{v_{i,2}} right) \
end{align*}
$$
Since there is no external force acting on the system and the total momentum of the system is equal to zero. So, the momentum of each object in the system can change but the arithmetic sum of the changes in the momentum of the two objects should be equals to zero. So, the answer is “Yes, the momentum of each ball is conserved during the collision.”
As the textbook mentions that the initial momentum of the object is given by the mass times the velocity.
$$
begin{align*}
vec{p} &= m ~ vec{v} \
end{align*}
$$
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
Rearrange and solve for the force:
$$
begin{align*}
vec{F} &= dfrac{ vec{I} }{ Delta t } \
&= dfrac{ Delta vec{p} }{ Delta t } \
&= dfrac{ dp }{ dt} \
end{align*}
$$
As we know the internal force generates the system momentum. As we see in the previous calculations, the external force is equal to the change in momentum with respect to time. So, the external force can change the total momentum of the system. As we know in the elastic collision, the momentum and the kinetic energy are conservative.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
Rearrange and solve for the force:
$$
begin{align*}
vec{F} &= dfrac{ vec{I} }{ Delta t } \
&= dfrac{ Delta vec{p} }{ Delta t } \
&= dfrac{ dp }{ dt} \
end{align*}
$$
As we know the internal force generates the system momentum. As we see in the previous calculations, the external force is equal to the change in momentum with respect to time. So, the external force can change the total momentum of the system. As we know in the elastic collision, the momentum and the kinetic energy are conservative. But in the inelastic collision, the momentum and the kinetic energy are non-conservative.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
According to conservation law of momentum, the impulse is equal to zero.
$$
begin{align*}
Delta p_{t} &= Delta p_{1} + Delta p_{2} \
&= 0 \
&= m_{1} ~ left( vec{v_{f,1}} – vec{v_{i,1}} right) + m_{2} ~ left( vec{v_{f,2}} – vec{v_{i,2}} right) \
m_{1} ~ left( vec{v_{f,1}} – vec{v_{i,1}} right) &= – m_{2} ~ left( vec{v_{f,2}} – vec{v_{i,2}} right) \
end{align*}
$$
Since there is no external force acting on the system and the total momentum of the system is equal to zero. So, the momentum of each object in the system can change but the arithmetic sum of the changes in the momentum of the two objects should be equals to zero. Since the momentum is a vector, then the two-component of the momentum in the $x$ and the $y$ directions can be conserved. In order to evaluate the kinetic energy, we use the following relation:
$$
begin{align*}
K.E &= dfrac{ 1}{2} ~ m ~ v^{2}
end{align*}
$$
Since the kinetic energy is a scalar quantity. So, there is no component of the scalar quantity perpendicular to each other. So, it is impossible to find the kinetic energy conserved in both the $x$ and the $y$ direction.
Solve for no friction force effect on the system:
Solve for the first object:
In order to evaluate the kinetic energy, we use the following relation:
$$
begin{align*}
K.E_{1} &= dfrac{ 1}{2} ~ m_{1} ~ v_{1}^{2}
end{align*}
$$
Solve for the second object:
In order to evaluate the kinetic energy, we use the following relation:
$$
begin{align*}
K.E_{2} &= dfrac{ 1}{2} ~ m_{2} ~ v_{2}^{2}
end{align*}
$$
According to the superposition principle, the total initial kinetic energy of the system is given by
$$
begin{align*}
K.E_{t} &= K.E_{1} + K.E_{2} \
&= dfrac{ 1}{2} ~ m_{1} ~ v_{1}^{2} + dfrac{ 1}{2} ~ m_{2} ~ v_{2}^{2}
end{align*}
$$
Since the mass of each object must be positive. Also, the square of the magnitude of the speed must be positive. Therefore, the total initial kinetic energy is positive. So, no kinetic energy is lost.
Use the Law of Conservation of Momentum to find the final speed of the objects and final energy of the system
$$
textbf{Solution:}
$$
$$
p_{i}=p_{f}
$$
$$
p_{i} m_{1,i}+m_2(0)=(m_1+m_2)v_f
$$
$$
frac{m_1}{m_1+m_2}v_{1,i}=v_f=frac{0.10kg}{0.10+0.20kg}(0.66m/s)=0.22m/s
$$
Now calculate the final kinetic energy
$$
K_f=frac{1}{2}(m_1+m_2)v^2_f=frac{1}{2}(0.10+0.20kg)(0.22m/s)^2=0.0073J
$$
$$
bf color{#4257b2} boxed{K_f=0.0073J}
$$
K_f=0.0073J
$$
Law of Conservation of Momentum can be used to determine the horizontal speed of the two train cars after collision. Assume each travels in the positive direction, we will calculate the kinetic energy of the system before and after collision and the energy lost in the collision.
$$
textbf{Solution:}
$$
Let $vec{p}_i= vec{p}_i$ and solve for $v_f$
$$
mv_{1,i}+mv_{2,i}=(m+m)v_f
$$
$$
v_f=frac{cancel{m}v_{1,i}+cancel{m}v_{2,i}}{2m}=frac{2.50+1.0m/s}{2}=bf color{#4257b2} boxed{1.75m/s}
$$
Let’s find the total kinetic energy
$$
textbf{Solution:}
$$
$$
KE_i=frac{1}{2}mv^2_{1,i}+frac{1}{2}mv^2_{2,i}=frac{1}{2}m(v^2_{1,i}+v^2_{2,i})
$$
$$
KE_i=frac{1}{2}(25000kg)(2.5m/s)^2+(1.0m/s)^2=90625J
$$
For final KE we get
$$
KE_f=frac{1}{2}mv^2_{1,f}+frac{1}{2}mv^2_{2,f}=frac{1}{2}(2m)v^2_f
$$
$$
=frac{1}{2}(2times 25000kg)(1.75m/s)^2=76563J
$$
$$
Delta KE = KE_i-KE_f=90625-76563J=bf color{#4257b2} boxed{14100J}
$$
$$
begin{equation}
v_{1:f}=frac{m_1-m_2}{m_1+m_2}cdot v_{1:i}\
end{equation}
$$
$$
begin{equation}
v_{2:f}=frac{2m_1}{m_1+m_2}cdot v_{1:i},
end{equation}
$$
where $f$ denotes ‘final’ and $i$ denotes ‘initial’ and $1$ and $2$ refer to ‘truck’ and ‘car’. To obtain the velocity of the truck after the collision, use $(1)$:
$$
v_{truck:f}=frac{m_{truck}-m_{car}}{m_{truck}+m_{car}}cdot v_{truck:i}=frac{1720-732}{1720+732}cdot (15.5)
$$
$$
boxed{v_{truck:f}=6.25:frac{text{m}}{text{s}}}
$$
To obtain the velocity of a car after the collision, use $(2)$:
$$
v_{car:f}=frac{2m_{truck}}{m_{truck}+m_{car}}cdot v_{truck:i}=frac{2cdot732}{1720+732}cdot (15.5)
$$
$$
boxed{v_{car:f}=21.75:frac{text{m}}{text{s}}}
$$
The velocities are in same direction.
v_{truck}=6.25:frac{text{m}}{text{s}}
$$
$$
v_{car}=21.75:frac{text{m}}{text{s}}
$$
$textbf{Concept}$
The total momentum of the system is conserved and is zero before and after collision. Law of Conservation of Momentum is used to find the momentum of 112 kg player and then compared to find the initial and the final momentum. for each
$$
textbf{Solution:}
$$
Find the initial velocity of the player by applying The Law of conservation of momentum
$$
vec{p}_{1,i}+vec{p}_{2,i}=0=m_1vec{p}_{1,i}+m_2vec{p}_{2,i}
$$
$$
vec{p}_{2,i}=-frac{m_1vec{p}_{1,i}}{m_2}=-frac{92kg times 7.5 m/s}{112kg}=-6.16m/s
$$
textbf{Concept}\
We will use conservation of momentum concept
textbf{Solution:}
For momentum of the +92kg player\
$$vec{p}_{1,i}=m_1vec{p}_{1,i}=92kg times 7.5 m/s=bf color{blue} boxed{690kgm/s}$$\\
c.)
textbf{Solution:}
$$Delta vec{p} = vec{p}_{1,f} – vec{p}_{1,i}=0-690 kg.m/s =bf color{blue} boxed{-690kg.m/s}$$
\\
d.)
The starting momentum of the player with weight 112 kg is $vec{p}_{2,i}=m_2vec{v}_{2,i} = (112kg)(-6.1m/s)=-690kg.m/s$ because the player has zero momentum after they collide. The change in momentum of the 112 kg player due to the collision is 690 kg.m/s we reach the result that the two changes in momentum are bf color{blue} boxed{mbox{equal and opposite in direction}}\\
e.)\
06.16 m/s is the initial speed of the 112 kg player.
Assuming zero friction between the skates and the ice we can use Law of Conservation of Momentum with the fact that players stick together after collision to calculate final velocity. Assume motion of player 1 be in positive x direction and player 2 be at an angle of $90^0$ measured counter clockwise from the positive x axis
$$
textbf{Solution:}
$$
From the Law of Conservation of Momentum along x axis we solve for $v_{x,f}$
$$
vec{p}_{1x,i}+vec{p}_{2x,i}=vec{p}_{2x,i}
$$
$$
mv+0=2mv_{x,f}
$$
$$
frac{1}{2}=v_{x,f}=frac{1}{2}(5.45m/s)=2.725m/s
$$
From the Law of Conservation of Momentum along y axis we solve for $v_{y,f}$
$$
vec{p}_{1y,i}+vec{p}_{2y,i}=vec{p}_{2y,i}
$$
$$
mv+0=2mv_{y,f}
$$
$$
frac{1}{2}=v_{y,f}=frac{1}{2}(5.45m/s)=2.725m/s
$$
Finally for $vec{v}_f$
$$
v_f=sqrt{v^2_{x,f}+v^2_{y,f}}
$$
$$
v_f=sqrt{(2.725m/s)^2+(2.725m/s)^2}=bf color{#4257b2} boxed{3.85m/s}
$$
v_f=3.85m/s
$$
Projection of the equation on the x-axis:
$$
begin{align*}
P_{1,x}&=P_{T,x}\
mv&=2mv_{f,x}\
v_{f,x}&=frac{1}{2}v=0.5*5.45frac{m}{s}=2.725frac{m}{s}
end{align*}
$$
Projection of the equation on the y-axis:
$$
begin{align*}
P_{1,x}&=P_{T,y}\
mv&=2mv_{f,y}\
v_{f,y}&=frac{1}{2}v=0.5*5.45frac{m}{s}=2.725frac{m}{s}
end{align*}
$$
Last step is to calculate the total final velocity;
$$
begin{align*}
v_f&=sqrt{v_{f,x}^2+v_{f,y}^2}\
v_f&=sqrt{2.725^2+2.725^2}=boxed{color{#4257b2}{3.85frac{m}{s}}}
end{align*}
$$
tt{$v_f=3.85frac{m}{s}$}
$$
This is the case of elastic collision in one dimension where stone 2 was initially at rest. Equation of velocities after elastic collision can be applied to find The final speed of the two stones. Assume $m_1$ and $m_2$ be the masses respectively and $v$ be the initial speed of stone 1.
$$
textbf{Solution:}
$$
Use the elastic collision equation to find $v_{2,f}$
$$
v_{2,f}=bigg(frac{2m_1}{m_1+m_2}bigg)v=bigg(frac{2(21kg)}{21+16kg}bigg)(1.7m/s)=bf color{#4257b2} boxed{1.9m/s}
$$
Again using the elastic collision equation to find $v_{1,f}$
$$
v_{1,f}=bigg(frac{m_1-m_2}{m_1+m_2}bigg)v=bigg(frac{21-16kg}{21+16kg}bigg)(1.7m/s)=bf color{#4257b2} boxed{0.23m/s}
$$
v_{2,f}=1.90m/s
$$
$$
v_{1,f}=0.23m/s
$$
This is the case of elastic collision in one dimension where stone 2 was initially at rest. Equation of velocities after elastic collision can be applied to find the final speed of the two stones. Assume $m_1$ and $m_2$ be the masses respectively and $v$ be the initial speed of stone 1.
$$
textbf{Solution:}
$$
Again using the elastic collision equation to find $v_{2,f}$
$$
v_{2,f}=bigg(frac{2m_1}{m_1+m_2}bigg)v Rightarrow = frac{v_{2,f}}{v}=frac{2m_1}{m_1+m_2}
$$
Now multiply both sides by $m_1+m_2$and divide both sides by $frac{v_{2,f}}{v}$ we get
$$
m_1+m_2=frac{2m_1}{v_{2,f}/{v}}
$$
Now subtract $m_1$ from both sides and substituting numerical values we get
$$
m_2=frac{v}{v_{2,f}}(2m_1)-m_1=frac{1.5m/s}{0.69m/s}(2times 16kg)-16kg)=bf color{#4257b2} boxed{54kg}
$$
Using elastic collision equation to find $v_{1,f}$
$$
textbf{Solution:}
$$
$$
v_{1,f}=bigg(frac{m_1-m_2}{m_1+m_2}bigg)v=bigg(frac{16-54kg}{16+54kg}bigg)(1.5m/s)=bf color{#4257b2} boxed{-0.81m/s}
$$
$textbf{Concept}$
Using Law of Conservation of Momentum to find the speed of bullet after the collision. as this is an inelastic collision there will be loss of kinetic energy. Find initial and final KEs and confirm the energy loss. Let b and B represents bullet and block respectively.
$$
textbf{Solution:}
$$
Let $vec{p}_{i}=vec{p}_{f}$ and solve for $vec{p}_{bf}$
$$
m_{b}v_{bi}+0=m_{b}v_{bf}+m_{B}v_{Bf}
$$
$$
v_{bf}=frac{m_{b}v_{bi}-m_{B}v_{Bf}}{{b}v_{bf}}
$$
$$
=frac{(0.0040kg)(650m/s)-(0.095kg)(23m/s)}{0.0040kg}=bf color{#4257b2} boxed{104m/s}
$$
The final kinetic energy is bf color{blue} boxed{mbox{less than}} the initial because energy is lost to the heating and deformation of the bullet and block.
$textbf{Concept}$
By the definition of $KE_i$
$$
KE_i=frac{1}{2}m_{b}v^2_{bi}=frac{1}{2}(0.0040kg)(650m/s)^2=bf color{#4257b2} boxed{850J}
$$
$$
textbf{Solution:}
$$
By the same definition we find $KE_f$
$$
KE_f=frac{1}{2}m_{b}v^2_{bf}+frac{1}{2}m_{B}v^2_{Bf}
$$
$$
=frac{1}{2})(0.0040kg)(104m/s)^2+frac{1}{2}(0.095kg)(23m/s)
$$
$$
KE_F=bf color{#4257b2} boxed{47J}
$$
104;m/s, less than, 850 J, 47 J
$$
The mass of the block is $m_{1} = 0.43 mathrm{~kg}$. The spring’s constant is $k = 20 mathrm{~N cdot m}$. The mass of the putty is $m_{2} = 0.05 mathrm{~kg}$. The speed of the putty is $v_{2} = 2.3 mathrm{~m/s}$. The putty and the block stick together $v_{f,1} = v_{f,1}$.
$textbf{Required: }$
Finding the spring stretch or compression.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
According to conservation law of momentum, the impulse is equal to zero.
$$
begin{align*}
Delta p_{t} &= Delta p_{1} + Delta p_{2} \
&= 0 \
&= m_{1} ~ left( vec{v_{f,1}} – vec{v_{i,1}} right) + m_{2} ~ left( vec{v_{f,2}} – vec{v_{i,2}} right) \
&= m_{1} ~ left( vec{v_{f}} – 0 right) + m_{2} ~ left( vec{v_{f}} – v_{2} right) \
&= v_{f} ~ left( m_{1} + m_{2} right) – m_{2} ~ v_{2} \
end{align*}
$$
Rearrange and solve for the mass of the findla speed of the block and the putty:
$$
begin{align*}
v_{f} &= dfrac{ m_{2} ~ v_{2} }{left( m_{1} + m_{2} right) } \
&= dfrac{ 0.05 mathrm{~kg} times 2.3 mathrm{~m/s} }{ left( 0.43 mathrm{~kg} + 0.05 mathrm{~kg} right) } \
&= 0.2396 mathrm{~m/s}
end{align*}
$$
According to Hooke’s law:
$$
begin{align*}
F &= – k ~ x \
end{align*}
$$
In order to evaluate the potential energy of the spring, we use the following relation:
$$
begin{align*}
U &= dfrac{1}{2} ~ k ~ x^{2} \
end{align*}
$$
In general, In order to evaluate the kinetic energy, we use the following relation:
$$
begin{align*}
K.E &= dfrac{1}{2} ~ m ~ v^{2} \
end{align*}
$$
According to conservation law of energy:
$$
begin{align*}
Delta E &= K.E – U \
&= 0 \
K.E &= U \
dfrac{1}{2} ~ m ~ v^{2} &= dfrac{1}{2} ~ k ~ x^{2} \
end{align*}
$$
Rearrange and solve for the spring’s compression $x$:
$$
begin{align*}
x &= sqrt{ dfrac{ m ~ v^{2} }{ k } } \
&= sqrt{ dfrac{ 0.43 mathrm{~kg} times left( 0.2396 mathrm{~m/s} right)^{2} }{ 20 mathrm{~N/m} } } \
&= 0.035 mathrm{~m}
end{align*}
$$
So, the distance the putty-block system compressed with is $3.5 mathrm{~cm}$.
For every case, a moving cart collides with one at rest so equation for elastic collision will given velocities of all carts. First use equation of collision between carts 4m and 2m and then 2m and m. Assume the 4m car be called cart 4, 2m be cart 2 and cart 1 be m.
$$
textbf{Solution:}
$$
Using the elastic collision equations to find the initial condition
$$
v_{4,f}=frac{m_4-m_2}{m_4+m_2}v_{4,i}=frac{4m-2m}{4m+2m}v=bf color{#4257b2} boxed{frac{1}{3}v}
$$
$$
v_{2,f}=frac{2m_4}{m_4+m_2}v_{4,i}=frac{2(4m)}{4m+2m}v=frac{4}{3}v
$$
Again using the elastic collision equations to for the second collision for this case cart2 has initial speed of $frac{4}{3}v$ we get
$$
v_{2,f}=frac{m_2-m_1}{m_2+m_1}v_{2,i}=frac{2m-m}{2m+m}frac{4}{3}v=bf color{#4257b2} boxed{frac{4}{9}v}
$$
$$
v_{1,f}=frac{2m_2}{m_2+m_1}v_{2,i}=frac{2(2m)}{2m+m}frac{4}{3}v=bf color{#4257b2} boxed{frac{16}{9}v}
$$
Check that $K_i= K_f$ by using kinetic energy equation and dividing both sides by $mv^2_o$ we get
textbf{Solution:}
$$frac{1}{2}(4m)v^2=frac{1}{2}(4m)(frac{1}{3}v)^2+frac{1}{2}(2m)(frac{4}{9}v)^2+frac{1}{2}(m)(frac{16}{9}v)^2$$
$$2=frac{2}{9}+frac{16}{81}+frac{256}{162}=frac{36}{162}+frac{32}{162}+frac{256}{162}=frac{324}{162}=2$$
$$bf color{blue} boxed{mbox{hence.. }K_i= K_f}$$
v_{4,f}=frac{1}{3}v
$$
$$
v_{2,f}=frac{4}{9}v
$$
$$
v_{1,f}=frac{16}{9}v
$$
$$
K_i= K_f
$$
The mass of the object $A$ is $m$. The mass of the object $B$ is $2 m$. The mass of the object $C$ is $dfrac{ m}{2}$.
Solve for the object $A$:
In order to evaluate the magnitude of the Momentum of the school’s bus, we use the formula that is given in the second yellow box:
$$
begin{align*}
p_{A} &= m_{A} ~ v_{A} \
end{align*}
$$
Solve for the object $B$:
In order to evaluate the magnitude of the Momentum of the school’s bus, we use the formula that is given in the second yellow box:
$$
begin{align*}
p_{B} &= m_{B} ~ v_{B} \
end{align*}
$$
since the two momentums are equal $p_{A} =p_{B}$, then we get
$$
begin{align*}
p_{A} &=p_{B} \
m_{A} ~ v_{A} &= m_{B} ~ v_{B} \
m ~ v_{A} &= 2 m ~ v_{B} \
end{align*}
$$
Rearrange and solve for the speed of the object $B$:
$$
begin{align*}
v_{B} &= dfrac{1}{2} ~ v_{A}
end{align*}
$$
Solve for the object $C$:
In order to evaluate the magnitude of the Momentum of the school’s bus, we use the formula that is given in the second yellow box:
$$
begin{align*}
p_{C} &= m_{C} ~ v_{C} \
end{align*}
$$
since the two momentums are equal $p_{A} =p_{C}$, then we get
$$
begin{align*}
p_{A} &=p_{C} \
m_{A} ~ v_{A} &= m_{C} ~ v_{C} \
m ~ v_{A} &= dfrac{ m}{2} ~ v_{C} \
end{align*}
$$
Rearrange and solve for the speed of the object $C$:
$$
begin{align*}
v_{C} &= 2 ~ v_{A}
end{align*}
$$
In order to evaluate the kinetic energy of the object $A$, we use the following relation:
$$
begin{align*}
K.E_{A} &= dfrac{1}{2} ~ m_{A} ~ v_{A}^{2} \
&= dfrac{1}{2} ~ m ~ v_{A}^{2}
end{align*}
$$
In order to evaluate the kinetic energy of the object $B$, we use the following relation:
$$
begin{align*}
K.E_{B} &= dfrac{1}{2} ~ m_{B} ~ v_{B}^{2} \
&= dfrac{1}{2} ~ 2 m ~ left( dfrac{1}{2} ~ v_{A} right)^{2} \
&= dfrac{1}{4} ~ m ~ v_{A}^{2} \
end{align*}
$$
In order to evaluate the kinetic energy of the object $C$, we use the following relation:
$$
begin{align*}
K.E_{C} &= dfrac{1}{2} ~ m_{C} ~ v_{C}^{2} \
&=dfrac{1}{2} ~ dfrac{m}{ 2} ~ left( 2~ v_{A} right)^{2} \
&= dfrac{1}{2} ~dfrac{m}{ 2} ~ 4~ v_{A}^{2} \
&=m ~ v_{A}^{2}
end{align*}
$$
So, the ranking of these objects in order of increasing kinetic energy is $K.E_{B} < K.E_{A} < K.E_{C}$.
The mass of the object $A$ is $m$. The mass of the object $B$ is $4 m$. The mass of the object $C$ is $dfrac{ m}{4}$.
Solve for the object $A$:
In order to evaluate the magnitude of the Momentum of object $A$, we use the following formula:
$$
begin{align*}
p_{A} &= m_{A} ~ v_{A} \
&= m ~ v_{A}
end{align*}
$$
In order to evaluate the kinetic energy of the object $A$, we use the following relation:
$$
begin{align*}
K.E_{A} &= dfrac{1}{2} ~ m_{A} ~ v_{A}^{2} \
&= dfrac{1}{2} ~ m ~ v_{A}^{2}
end{align*}
$$
Solve for the object $B$:
In order to evaluate the magnitude of the Momentum of the object $B$, we use the following formula:
$$
begin{align*}
p_{B} &= m_{B} ~ v_{B} \
&= 4 m ~ v_{B}
end{align*}
$$
In order to evaluate the kinetic energy of the object $B$, we use the following relation:
$$
begin{align*}
K.E_{B} &= dfrac{1}{2} ~ m_{B} ~ v_{B}^{2} \
&= dfrac{1}{2} ~4 m ~ v_{B}^{2} \
&= 2 m ~ v_{B}^{2} \
end{align*}
$$
Since the two kinetic energies are equal, then we get
$$
begin{align*}
K.E_{A} &= K.E_{B} \
dfrac{1}{2} ~ m ~ v_{A}^{2} &= 2 m ~ v_{B}^{2} \
end{align*}
$$
Rearrange and solve for $v_{B}$:
$$
begin{align*}
v_{B} &= sqrt{ dfrac{1}{4} ~ v_{A}^{2}}
end{align*}
$$
Solve for the object $C$:
In order to evaluate the magnitude of the Momentum of the object, we use the following relation:
$$
begin{align*}
p_{C} &= m_{C} ~ v_{C} \
&= dfrac{ m}{4} ~ v_{C}
end{align*}
$$
In order to evaluate the kinetic energy of the object $C$, we use the following relation:
$$
begin{align*}
K.E_{C} &= dfrac{1}{2} ~ m_{C} ~ v_{C}^{2} \
&= dfrac{1}{2} ~ dfrac{ m}{4} ~ v_{C}^{2} \
&= dfrac{ m}{8} ~ v_{C}^{2} \
end{align*}
$$
Since the two kinetic energies are equal, then we get
$$
begin{align*}
K.E_{A} &= K.E_{C} \
dfrac{1}{2} ~ m ~ v_{A}^{2} &= dfrac{m}{8} ~ v_{C}^{2} \
end{align*}
$$
Rearrange and solve for $v_{C}$:
$$
begin{align*}
v_{C} &= sqrt{4 ~ v_{A}^{2}}
end{align*}
$$
Substituting in the equation of the momentum of the object $B$, then we get
$$
begin{align*}
p_{B} &= 4 m ~ v_{B} \
&= 4 m ~ sqrt{ dfrac{1}{4} ~ v_{A}^{2}} \
&= 2 m ~ v_{A}
end{align*}
$$
Substituting in the equation of the momentum of the object $C$, then we get
$$
begin{align*}
p_{C} &= dfrac{m}{4} ~ v_{C} \
&=dfrac{m}{4} ~ sqrt{ 4 ~ v_{A}^{2}} \
&= dfrac{ m}{2} ~ v_{A}
end{align*}
$$
So, the ranking of these objects in order of increasing momentum is $p_{C} < p_{A} < p_{B}$.
In order to evaluate the magnitude of the Momentum, we use the following formula:
$$
begin{align*}
p &= m ~ v \
end{align*}
$$
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
So, the larger change in the momentum leads to a large impulse. So, the rubber bullet that bounces off the wood has changed in momentum greater than the metal bullet that embeds itself in the wood.
The answer is “A. The change in momentum when a bullet rebounds is twice as much as when it is brought to rest.”
(b) A. The change in momentum when a bullet rebound is twice as much as when it is brought to rest.
The magnitude of the force that exerts by the rocket is $F = 25 mathrm{~N}$. The mass of the probe is $m = 722 mathrm{~kg}$. The speed of the probe is $v = 1 mathrm{~s}$.
$textbf{Required: }$
Finding the time interval that the rocket fire to change the speed.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
end{align*}
$$
Rearrange and solve for the time interval that the rocket fire to change the speed:
$$
begin{align*}
Delta t &= dfrac{ I }{ F} \
&= dfrac{ Delta p }{F} \
&= dfrac{ m ~ Delta v }{ F} \
&= dfrac{ 722 mathrm{~kg} times left( 1 mathrm{~m/s} – 0 mathrm{~m/s} right) }{ 25 mathrm{~N} } \
&= 28.88 mathrm{~s}
end{align*}
$$
So, the time interval that the rocket fire to change the speed is $28.88 mathrm{~s}$.
$textbf{Concept}$
We need to have constant momentum in order to find the speed of the 2nd car and only then we can calculate the initial and final kinetic energies of the entire system to see if any energy is lost. For a collision to be inelastic we need to have some energy loss in the process.
$$
textbf{Solution:}
$$
Let $vec{p}_{i}=vec{p}_{f}$ and solve for $v_{2f}$
$$
m v_{1,i}+0=mv_{1,f}+(frac{1}{2})v_{2,f}
$$
$$
v_{2,f}=frac{m(v_{1,i}-v_{2,f})}{m/2}=2(v-v/3)=bf color{#4257b2} boxed{frac{4}{3}v}
$$
$textbf{Concept}$
Use the definition to find $KE_i$
$$
textbf{Solution:}
$$
$$
KE_i=frac{1}{2}mv^2
$$
Now using equation 7-6 to find the $K_f$
$$
K_f=frac{1}{2} m v^2_{1f}+frac{1}{2}(frac{1}{2})m v^2_{2f}
$$
$$
=frac{1}{2}m(frac{1}{3}v)^2+frac{1}{2}(frac{1}{2}m)(frac{4}{3}v)^2=frac{1}{2}mv^2(frac{1}{9}+frac{16}{18})=frac{1}{2}mv^2
$$
Since because $K_i=K_f$ we found that the collision was bf $text{color{#4257b2} boxed{elastic}}$
dfrac{4}{9}v,;; elastic
$$
The weight of the apple is $F= 2.7 mathrm{~N}$. The time interval that the apple takes to fall is $Delta t = 1.4 mathrm{~s}$.
$textbf{Required: }$
(a) Finding the change in the apple’s momentum per second.
(b) Fidning the total change in the momentum.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
Rearrange and solve for the change in the apple’s momentum per second:
$$
begin{align*}
F &= dfrac{ I }{ Delta t } \
&= dfrac{ Delta p }{ Delta t } \
&= 2.7 mathrm{~N}
end{align*}
$$
So, the change in the apple’s momentum per second is $2.7 mathrm{~N}$.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= 2.7 mathrm{~N} times 1.4 mathrm{~s} \
&= 3.78 mathrm{~kg cdot m/s}
end{align*}
$$
So, the total change in the momentum is $3.78 mathrm{~kg cdot m/s}$.
(b) The total change in the momentum is $3.78 mathrm{~kg cdot m/s}$.
The mass of the helmat is $m_{1} = 1.3 mathrm{~kg}$. The initial speed of the helmat is $v_{f,1} = 6.5 mathrm{~m/s}$. The direction of the speed is $theta = 11^{circ}$. The final speed of the helmat is $v_{f,2} = 0.25 mathrm{~m/s}$.
$textbf{Required: }$
Finding the mass of the hockey player.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
According to conservation law of momentum, the impulse is equal to zero.
$$
begin{align*}
Delta p_{t} &= Delta p_{1} + Delta p_{2} \
&= 0 \
&= m_{1} ~ left( vec{v_{f,1}} – vec{v_{i,1}} right) + m_{2} ~ left( vec{v_{f,2}} – vec{v_{i,2}} right) \
&= m_{1} ~ left( vec{v_{f,1}} – 0right) + m_{2} ~ left( vec{v_{f,2}} – 0 right) \
end{align*}
$$
Rearrange and solve for the mass of the hockey player:
$$
begin{align*}
m_{2} &= – dfrac{ m_{1} ~ v_{f,1} ~ cos left( theta right) }{ v_{f,2} } \
&= – dfrac{ 1.3 mathrm{~kg} times 6.5 mathrm{~m/s} times cos left( 11^{circ} right) }{ – 0.25 mathrm{~m/s} } \
&= 33.179 mathrm{~kg}
end{align*}
$$
So, the mass of the hockey player is $33.179 mathrm{~kg}$.
$textbf{Concept}$
With the law of conservation of energy we will try to find the speed of the apple after it has fallen from rest to a given distance. We use the momentum-impulse theorem then, in the shape of Newtons second law, to calculate the average force needed to bring the apple to rest. Important thing is that couple of forces act on the apple where as it is being brought to rest, the force of gravity and the force of your hand.
$$
textbf{Solution:}
$$
Using the Law of Conservation of energy to find the apple’s speed we get:
$$
0+PE_i=KE_f+0
$$
$$
mgh_i=frac{1}{2}mv^2_f
$$
$$
sqrt{2gh_i}=v_f=sqrt{2(9.81m/s^2)(3.5m)}=bf color{#4257b2} boxed{8.3m/s}
$$
$textbf{Concept}$
Using momentum-impulse theorem in the shape of newton’s second law we get:
$$
textbf{Solution:}
$$
$$
Sigma F = F_{hand}-mg=frac{Delta p}{Delta t}
$$
$$
F_{hand}=mg+frac{m(v_f-v_i)}{Delta t}
$$
$$
=(0.22kg)(9.81m/s^2)+frac{(0.22kg)(8.3)}{0.28s}
$$
$$
=2.2N+6.5N=bf color{#4257b2} boxed{8.7N}
$$
v_f=8.3m/s,;;v_f=8.3m/s
$$
The raindrops speed is $v = 10 mathrm{~m/s}$. The time interval of the rain falling is $Delta t = 9 mathrm{~hr}$. The mass of the cubic meter of water is $m = 1000 mathrm{~kg}$. The length of the rain falling is $L = 0.79 mathrm{~m}$.
$textbf{Required: }$
Finding the average exerted force.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
Rearrange and solve for the average exerted force by $1$ square meter of ground to stop the falling raindrops during the storm:
$$
begin{align*}
F &= dfrac{ I }{ Delta t } \
&= dfrac{ Delta p }{ Delta t } \
&= dfrac{ Delta m ~ v }{ Delta t } \
&= dfrac{ 0.79 mathrm{~m} times 1000 mathrm{~kg} times 10 mathrm{~m/s} }{ 9 times 60 times 60 mathrm{~s} } \
&= 0.244 mathrm{~N}
end{align*}
$$
So, the average exerted force by $1$ square meter of ground to stop the falling raindrops during the storm is $0.244 mathrm{~N}$.
This is the case of a completely inelastic collision as the two cars stick together. We will use the conservation of momentum to calculate the mass of the minivan. Let eastward be the positive direction.
$$
textbf{Solution:}
$$
From the statement of Law of Conservation of Momentum
$$
vec{p}_{i}=vec{p}_{f}
$$
$$
m_{car}v_{car,i}+m_{mv}v_{mv,i}=(m_{car}+m_{mv})vec{v}_f
$$
Rearranging terms we get
$$
m_{car}v_{car,i}+m_{mv}v_{mv,i}=m_{car}vec{v}_f+m_{mv}vec{v}_f
$$
$$
m_{car}v_{car,i}-m_{car}vec{v}_f=m_{mv}v_{mv,i}-m_{mv}vec{v}_f
$$
$$
m_{car}(v_{car,i}-vec{v}_f)=m_{mv}(v_{mv,i}-vec{v}_f)
$$
$$
m_{car}frac{v_{car,i}-vec{v}_f}{vec{v}_f-v_{mv,i}}=m_{mv}=(1540kg)frac{(-12m/s)-(+1.5m/s)}{(+1.5m/s)-(+9.4m/s)}
$$
$$
m_{mv}=bf color{#4257b2} boxed{2630kg=2.6times 10^3kg}
$$
m_{mv}=2630kg=2.6times 10^3kg
$$
We will use conservation of momentum to find the horizontal speed of the bullet $m$ and block $M$ after the collision. We will calculate the kinetic energy of the bullet-block system, and then use the work-energy equation to find the frictional forces. Lastly, we use the weight of the bullet-block system to find the coefficient of kinetic friction.
$$
textbf{Solution:}
$$
From the statement of Law of Conservation of Momentum
$$
vec{p}_{i}=vec{p}_{f}
$$
$$
mv_{i}+M(0)=(m+M)v_f
$$
Solving for $v_f$
$$
v_f=bigg[frac{m}{m+M}bigg]v_i=bigg[frac{0.011kg}{0.0011+1.7kg}bigg](670m/s)=4.31m/s
$$
Now calculate the kinetic Energy of the bullet block system
$$
KE=frac{1}{2}(m+M)v^2_f=frac{1}{2}(0.011+1.7kg)(4.31m/s)^2=15.9J
$$
Now use the work energy theorem for calculating friction
$$
W=-fd=Delta KE
$$
$$
ffrac{KE_f-KE_i}{d}=-frac{0-15.9J}{2.4m}=6.63N
$$
Finally use the relationship between friction and normal force to find the coefficient of kinetic friction
$$
f=mu_k N=mu_k(m+M)g
$$
$$
mu_k=frac{f}{(m+M)g}=frac{6.63N}{(0.011+1.7kg)(9.81m/s^2)}=bf color{#4257b2} boxed{0.39}
$$
mu_k=0.39
$$
Here the Law of conservation of momentum will be used to find the horizontal speed of the bullet and block, then we will use the equations that apply to a horizontally-launched projectile to calculate the landing site of the bullet-block system. Assume $m$= the mass of the bullet, $M$= the mass of the block, and $v_i$ = the initial speed of the bullet, and $h$ = the height of the table.
$$
textbf{Solution:}
$$
Let $vec{p}_{i}=vec{p}_{f}$ and solve for $v_f$
$$
mv_i+M(0)=(m+M)v_f
$$
$$
v_f=frac{m}{m+M}v_i=frac{0.0105kg}{0.0105+1.35kg}(715m/s)=5.52m/s
$$
Now find the time needed for bullet block system to drop from height $h$ The time postion equation are present in cahpter 4
$$
y=y_i+v_{y,i}t-frac{1}{2}gt^2
$$
$$
0=h+0times t-frac{1}{2}gt^2
$$
$$
h=frac{1}{2}gt^2 Rightarrow t=sqrt{frac{2h}{g}}=sqrt{frac{2(0.782m)}{9.81m/s^2}}=0.399s
$$
Finally find the horizontal distance travelled in the time the system was falling
$$
x_f=x_i+v_{x,i}t
$$
$$
d=x_f-x_i=v_{x,i}t=v_ft=(5.52m/s)(0.399s)=bf color{#4257b2} boxed{2.20m}
$$
d=2.20m
$$
Here we will use equation of conservation of momentum to calculate the speed of the carts for the case of before and after collisions. Since the momentum remains the same, there is no need to calculate the intermediate speed of carts 2 and 3 before collision. Finally, calculate the ratio of the final kinetic energy to initial kinetic energy.
$$
textbf{Solution:}
$$
let $vec{p}_{i}=vec{p}_{f}$ and solve for $v_f$
$$
mv+2mv+0=(m+2m+4m)v_f
$$
$$
3v=7v_f Rightarrow v_f=bf color{#4257b2} boxed{frac{3}{7}v}
$$
textbf{Concept:}
$$
Now calculate $K_f/K_i$
$$
textbf{Solution:}
$$
$$
frac{K_f}{K_i}=frac{frac{1}{2}(7m)(frac{3}{7}v)^2}{frac{1}{2}(3m)v^2}=bf color{#4257b2} boxed{frac{3}{7}}
$$
v_f=frac{3}{7}v
$$
$$
frac{K_f}{K_i}=frac{3}{7}
$$
The initial speed of the spacecraft is $v_{i}$ to the left. The planet’s speed is $u$ to the right. The final speed of the spacecraft is $v_{f}$ to the right. The relative speed of approach is equal to the relative speed of departure.
$textbf{Required: }$
Finding the approach speed of the spacecraft.
In order to evaluate the approach speed of the spacecraft, we use the following relation:
$$
begin{align*}
v_{app} &= v_{p,i} – v_{s,i} \
&= u – left( – v_{i} right) \
&= u + v_{i}
end{align*}
$$
So, the answer is “A. $v_{i} + u$”.
The initial speed of the spacecraft is $v_{i}$ to the left. The planet’s speed is $u$ to the right. The final speed of the spacecraft is $v_{f}$ to the right. The relative speed of approach is equal to the relative speed of departure.
$textbf{Required: }$
Finding the departure speed of the spacecraft.
In order to evaluate the departure speed of the spacecraft, we use the following relation:
$$
begin{align*}
v_{dep} &= v_{s,f} – v_{p,i} \
&= v_{f} – u \
end{align*}
$$
So, the answer is “B. $v_{f} – u$”.
The initial speed of the spacecraft is $v_{i}$ to the left. The planet’s speed is $u$ to the right. The final speed of the spacecraft is $v_{f}$ to the right. The relative speed of approach is equal to the relative speed of departure.
$textbf{Required: }$
Finding the approach speed of the spacecraft.
In order to evaluate the approach speed of the spacecraft, we use the following relation:
$$
begin{align*}
v_{app} &= v_{p,i} – v_{s,i} \
&= u – left( – v_{i} right) \
&= u + v_{i}
end{align*}
$$
In order to evaluate the departure speed of the spacecraft, we use the following relation:
$$
begin{align*}
v_{dep} &= v_{s,f} – v_{p,i} \
&= v_{f} – u \
end{align*}
$$
Since the approach speed is equal to the departure speed of the spacecraft. Rearrange and solve for the final speed $v_{f}$:
$$
begin{align*}
v_{app} &= v_{dep} \
u + v_{i} &= v_{f} – u \
v_{f} &= v_{i} + u + u \
&= v_{i} + 2 u \
end{align*}
$$
So, the answer is “C. $v_{i} + 2 u$”.

