
All Solutions
Page 668: Assessment
by
$$
Delta y=frac{Dlambda}{d}
$$
So the difference is proportional to the wavelength $lambda$. Now
from the figure we can see that the separation between maxima dicreases
in the figure (b). Hence the wavelength of the light represented in
the figure (b) is smaller than 550 nm.
$$
dsintheta=mlambda
$$
In the given problme we have $theta=0.067text{textdegree}$, $m=1$, and
$lambda=520$ nm. Therefore the slit seperation $d$ is given by
$$
d=frac{mlambda}{sintheta}=frac{1left(520 {rm nm}right)}{sin0.067text{textdegree}}=445times10^{3} {rm nm}=445 {rm mu m}
$$
$$
begin{align*}
m &= 3 \
d &= 4.1 cdot 10^{-4} text{ m} \
theta &= 0.26 text{textdegree}
end{align*}
$$
The wavelength of the light that passes on a third bright fringe in a two-slit experiment can be obtain by applying the expression :
$$
begin{align*}
d sin theta &= m lambda \
lambda &= dfrac{d sin theta}{m} \
&= dfrac{4.1 cdot 10^{-4} text{ m} (sin 0.26 text{textdegree})}{3}
end{align*}
$$
$$
{boxed{lambda = 620.17 text{ nm}}}
$$
{lambda = 620.17 text{ nm}}
$$
constructive interference. This is possible if the phase difference
is either 0 or integer multiple of $2pi$ rad. Now we know that the
phase difference at a dstance is given by
$$
phi=frac{2pi x}{lambda}
$$
So we must have
$$
begin{align*}
& phi_{1}-phi_{2}=2pi n\
Rightarrow & frac{2pi x_{1}}{lambda}-frac{2pi x_{2}}{lambda}=2pi n\
Rightarrow & frac{left(x_{1}-x_{2}right)}{lambda}=n
end{align*}
$$
Now since $x_{1}neq x_{2}$, $n$ can not be zero. So for the largest
wavelength we must have $n=1$, so we have
$$
lambda=left(x_{1}-x_{2}right)=left(450 {rm m}-150 {rm m}right)=300 {rm m}
$$
So largest possible wavelength is 300 m.
that point. Hence this is possible if the phase difference is odd
multiple of the $pi/2$ rad.
The phase difference at a distance $x$ is given by
$$
phi=frac{2pi x}{lambda}
$$
So the phase difference at point P is given by
$$
begin{align*}
& deltaphi=frac{2pi x_{1}}{lambda}-frac{2pi x_{2}}{lambda}=left(2n+1right)frac{pi}{2}\
Rightarrow & left(x_{1}-x_{2}right)=left(2n+1right)frac{lambda}{2}
end{align*}
$$
For largest possible lambda $n$ should be zero. Hence we have
$$
lambda=2left(x_{1}-x_{2}right)=2left(450 {rm m}-150 {rm m}right)=600 {rm m}
$$
So the largest possible wavelength for a destructive interferene at
P is 600 m
75 m away from the point P. Now she is traveling at a speed of 1.1
m/s. Hence the time taken to travel 75 m distance is given by
$$
t=frac{75 {rm m}}{1.1 {rm m/s}}=68.2 {rm s}
$$
After 68.2 s she will reach to the next location with maximum signal.
$$
begin{align*}
m &= 1 \
d &= 5.1 cdot 10^{-6} text{ m} \
lambda &= 550 text{ nm}
end{align*}
$$
The angle to the first bright fringe above the central bright fringe in a two-slit experiment can be obtain by applying the expression :
$$
begin{align*}
d sin theta &= m lambda \
sin theta &= dfrac{m lambda}{d} \
theta &= {sin}^{-1} left( dfrac{m lambda}{d} right) \
&= {sin}^{-1} left( dfrac{1 (550 cdot 10^{-9} text{ m})}{5.1 cdot 10^{-6} text{ m}} right)
end{align*}
$$
$$
{boxed{theta = 6.19 text{textdegree}}}
$$
{theta = 6.19 text{textdegree}}
$$
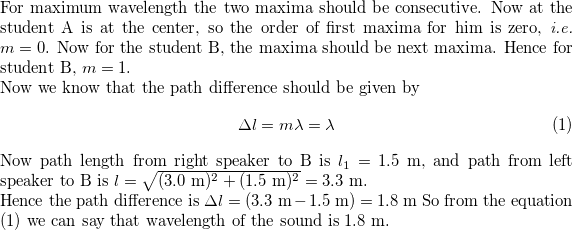


$6.0 {rm mm}$, so we have $Delta y=6.0 {rm mm}$. We know that
seperation between two fringe is given by
$$
Delta y=frac{Dlambda}{d}
$$
We have $lambda=632.8times10^{-9} {rm m}$, and $D=1.40 {rm m}$.
So from the above equation we can write that
$$
d=frac{Dlambda}{Delta y}=frac{left(1.40 {rm m}right)left(632.8times10^{-9} {rm m}right)}{left(6.0times10^{-3} {rm m}right)}=1.5times10^{-5} {rm m}=15 {rm mu m}
$$
$$
begin{align*}
m &= 1 \
d &= 132 cdot 10^{-6} text{ m} \
L &= 1.20 text{ m} \
y &= 6 text{ mm}
end{align*}
$$
$textbf{(a)}$ To find the wavelength, we need to determine first the angle for the first-order bright fringe using the relation for linear distance from the central bright fringe then use the angle to calculate the wavelength of the monochromatic light.
Solving for the angle, $theta$ :
$$
begin{align*}
y &= L tan theta \
theta &= {tan}^{-1} left( dfrac{y}{L} right) \
&= {tan}^{-1} left( dfrac{0.006 text{ m}}{1.20 text{ m}} right) \
theta &= 0.286 text{textdegree}
end{align*}
$$
Applying the expression for bright fringes to solve for the wavelength for $m = 1$ :
$$
begin{align*}
d sin theta &= m lambda \
lambda &= dfrac{d sin theta}{m} \
&= dfrac{132 cdot 10^{-6} text{ m} ~ (sin 0.286 text{textdegree})}{1}
end{align*}
$$
$$
{boxed{lambda = 660 text{ nm}}}
$$
$textbf{(b)}$ $textbf{move farther apart}$ to each other
$$
begin{align*}
m &= 1 \
d &= 0.0220 text{ mm} \
lambda &= 632.8 text{ nm} \
y &= 2.5 text{ cm}
end{align*}
$$
Calculating for the angle for $m = 1$ :
$$
begin{align*}
d sin theta &= m lambda \
sin theta &= dfrac{m lambda}{d} \
theta &= {sin}^{-1} left( dfrac{m lambda}{d} right) \
&= {sin}^{-1} left( dfrac{1 (632.8 cdot 10^{-9} text{ m})}{0.0220 cdot 10^{-3} text{ m}} right) \
theta &= 1.648 text{textdegree}
end{align*}
$$
$$
begin{align*}
y &= L tan theta \
L &= dfrac{y}{tan theta} \
&= dfrac{2.5 text{ cm}}{(tan 1.648 text{textdegree})}
end{align*}
$$
$$
{boxed{L = 86.9 text{ cm}}}
$$
{L = 86.9 text{ cm}}
$$
$$
2n_{film}d=2left(n_{film}right)frac{lambda}{4}
$$
So the phase difference due to traveling in the film is
$$
phi=2left(n_{film}right)frac{lambda}{4}left(frac{2pi}{lambda}right)=n_{film}pi {rm rad}
$$
So the path difference in all the 4 cases are $1.5pi, 1.5pi 1.6pi 1.6pi$
rad
In the first cases, in the both interface, light is traveling from
denser to lighter medium. Hence the phase difference due reflection
is zero. So the total phase difference is $1.5pi$ rad
In the second case, light is traveling from lighter to denser medium
in both interfaces. Hence reflected light is getting a phase shift
of $pi$ rad in both case. Hence phase difference due to reflected
light is zero. Hence the overall phase difference is $1.6pi$ rad
In the third case the first interface will suffer $pi$rad phase
shift but in second interface phase shift is zero. Hence the total
phase difference of the light is $left(1.6pi+piright)=2.6pi$
rad.
In the fourth case, the reflection in first interface suffer $pi$
rad phase shift and second surface suffer no phase shift. So the total
phase difference is $1.6pi+pi=2.6pi$ rad.
For constructive interference the total phase shift should be equal
to $0$ or integer multiple of $2pi$ rad. But none of the four case
satisfy this. Hence there will be no constructive interference.
The effective path length if there is no shift is given by
$$
begin{aligned}
2d = mlambda
end{aligned}
$$
Whereas, the effective path length if there is a shift is given by
$$
begin{aligned}
2d + frac{lambda}{2} = mlambda
end{aligned}
$$
where $d$ is the slit distance.
$$
begin{aligned}
2d &= mlambda \ 2 left(frac{lambda}{2}right) &= mlambda \ m &= 1
end{aligned}
$$
Since the effective path length is an integer, the reflected light ray will undergo **constructive interference**.
$$
begin{aligned}
2d &= mlambda \ 2 left(frac{lambda}{2}right) &= mlambda \ m &= 1
end{aligned}
$$
Since the effective path length is an integer, the reflected light ray will undergo **constructive interference**.
$$
begin{aligned}
2d + frac{lambda}{2} &= mlambda \ 2 left(frac{lambda}{2}right) + frac{lambda}{2} &= mlambda \ frac{3lambda}{2} &= mlambda \ m &= frac{3}{2}
end{aligned}
$$
Since the effective path length is half of an integer, the reflected light ray will undergo **destructive interference**.
$$
begin{aligned}
2d + frac{lambda}{2} &= mlambda \ 2 left(frac{lambda}{2}right) + frac{lambda}{2} &= mlambda \ frac{3lambda}{2} &= mlambda \ m &= frac{3}{2}
end{aligned}
$$
Since the effective path length is half of an integer, the reflected light ray will undergo **destructive interference**.
$$
begin{align*}
m &= 0 \
t &= 117 text{ nm} \
lambda &= 615 text{ nm}
end{align*}
$$
The index of refraction of the soap film, $n$ , as it experiences a constructive interference can be calculated by using the expression of condition for constructive interference in a thin film :
$$
begin{align*}
2 n t &= left( m + dfrac{1}{2} right) lambda \
n &= dfrac{left( m + dfrac{1}{2} right) lambda}{2 t} \
&= dfrac{left( 0 + dfrac{1}{2} right) 615 text{ nm}}{2 (117 text{ nm})} \
&= dfrac{307.5 text{ nm}}{234 text{ nm}}
end{align*}
$$
$$
{boxed{n = 1.314}}
$$
{n = 1.314}
$$
$$
begin{align*}
m &= 0 \
lambda &= 652 text{ nm} \
n &= 1.33
end{align*}
$$
In a constructive interference, the minimum thickness of the soap film corresponds to the smallest value of $m$ which is zero. So the minimum thickness can be calculated using the expression of condition for constructive interference in a thin film :
$$
begin{align*}
2 n t &= left( m + dfrac{1}{2} right) lambda \
t &= dfrac{left( m + dfrac{1}{2} right) lambda}{2 n} \
&= dfrac{left( 0 + dfrac{1}{2} right) 652 text{ nm}}{2 (1.33)} \
&= dfrac{326 text{ nm}}{2.66}
end{align*}
$$
$$
{boxed{t = 122.56 text{ nm}}}
$$
{t = 122.56 text{ nm}}
$$
$$
2n_{film}d=mlambda
$$
Here we have $n_{film}=1$ and $m=150$ and $d=4.7times10^{-5} {rm m}$.
Hence we have
$$
lambda=frac{2n_{film}d}{m}=frac{2left(1right)left(4.7times10^{-5} {rm m}right)}{150}=6.27times10^{-7} {rm m}=627 {rm nm}
$$



$$
begin{align*}
t &= 825 text{ nm} \
lambda &= 400 – 700 text{ nm} \
n &= 1.33
end{align*}
$$
For $m = 1$ :
$$
begin{align*}
2 n t &= m lambda_1 \
lambda_1 &= dfrac{2 n t}{m} \
&= dfrac{2 (1.33) (825 text{ nm})}{1} \
lambda_1 &= 2194.5 text{ nm}
end{align*}
$$
For $m = 2$ :
$$
begin{align*}
2 n t &= m lambda_2 \
lambda_2 &= dfrac{2 n t}{m} \
&= dfrac{2 (1.33) (825 text{ nm})}{2} \
lambda_2 &= 1097.3 text{ nm}
end{align*}
$$
$$
begin{align*}
2 n t &= m lambda_3 \
lambda_3 &= dfrac{2 n t}{m} \
&= dfrac{2 (1.33) (825 text{ nm})}{3} \
lambda_3 &= 731.5 text{ nm}
end{align*}
$$
For $m = 4$ :
$$
begin{align*}
2 n t &= m lambda_4 \
lambda_4 &= dfrac{2 n t}{m} \
&= dfrac{2 (1.33) (825 text{ nm})}{4} \
lambda_4 &= boxed{548.6 text{ nm}}
end{align*}
$$
$$
begin{align*}
2 n t &= m lambda_5 \
lambda_5 &= dfrac{2 n t}{m} \
&= dfrac{2 (1.33) (825 text{ nm})}{5} \
lambda_5 &= boxed{438.9 text{ nm}}
end{align*}
$$
For $m = 6$ :
$$
begin{align*}
2 n t &= m lambda_6 \
lambda_6 &= dfrac{2 n t}{m} \
&= dfrac{2 (1.33) (825 text{ nm})}{6} \
lambda_6 &= 365.8 text{ nm}
end{align*}
$$
Therefore, the wavelengths that will experience destructive interference is ${boxed{438.9 text{ nm}}}$ and ${boxed{548.6 text{ nm}}}$.
$$
begin{align*}
d &= 4.9 cdot 10^{-5} text{ m} \
lambda &= 695 text{ nm}
end{align*}
$$
$textbf{(a)}$ The value of $m$ from which the light is eliminated by destructive interference can be calculated using the condition for bright fringes :
$$
begin{align*}
dfrac{1}{2} lambda + 2 d &= left( m + dfrac{1}{2} right) lambda \
m + dfrac{1}{2} &= dfrac{dfrac{1}{2} lambda + 2 d}{lambda} \
m &= left( dfrac{dfrac{1}{2} lambda + 2 d}{lambda} right) – dfrac{1}{2} \
&= left[ dfrac{dfrac{1}{2} (695 cdot 10^{-9}) + (2 times 4.9 cdot 10^{-5})}{695 cdot 10^{-9}} right] – dfrac{1}{2} \
&= left( dfrac{9.835 cdot 10^{-5}}{695 cdot 10^{-9}}right) – dfrac{1}{2}
end{align*}
$$
$$
{boxed{m = 141}}
$$
$textbf{(b)}$ $textbf{increase}$

but light reflected from the bottom surface will experience a phase
shift of $pi$ rad. Hence for constructive interference the distance
must be a odd multiple of half of the wavelength $left(lambda/2right)$
and for destructive interference the separation must be a even multiple
of half of the wavelength.
Here we have:
$$
lambda/2=left(343 {rm nm}right)/2=171.5 {rm nm}
$$
$$
d=0.600 {rm mu m}=600 {rm nm}
$$
Hence ratio of wavelength to separation is:
$$
frac{d}{lambda/2}=frac{600 {rm nm}}{171.5 {rm nm}}=3.5
$$
So the interference will be neither constructive nor destructive.
$$
begin{align*}
m &= 1 \
lambda &= 412 text{ nm}
end{align*}
$$
$textbf{(a)}$ The minimum separation distance, $d$ , from the two glass plates in order for the light to experience a constructive interference can be calculated using the condition for bright fringes with the value of $m$ equal to 1 :
$$
begin{align*}
dfrac{1}{2} lambda + 2 d &= m lambda \
2 d &= m lambda – dfrac{1}{2} lambda \
d &= dfrac{lambda left( m – dfrac{1}{2} right)}{2} \
&= dfrac{412 text{ nm} left(1 – dfrac{1}{2} right)}{2}
end{align*}
$$
$$
{boxed{d = 103 text{ nm}}}
$$
$textbf{(b)}$ The separation distance, $d$ , $textbf{does not depend}$ on the index of refraction of both glass plates.
The condition of destructive interference here is
$$
2nd=mlambda
$$
Here $lambda=589 {rm nm}$and $n=1$
Now at the left end, width $d_{1}=0.0500 {rm mm}=50000 {rm nm}$,
So the order of interference is
$$
m_{1}=frac{2nd_{1}}{lambda}=frac{2(1)(50000 {rm nm})}{589 {rm nm}}=169.8
$$
At the right end, $d=0.0520 {rm mm}=52000 {rm nm}$
So the order of interference is
$$
m_{2}=frac{2nd_{2}}{lambda}=frac{2(1)(52000 {rm nm})}{589 {rm nm}}=176.6
$$
So the change in order is $176.6-169.8=6.8$. This change occurs in
7 cm. The distance between two dark fringe is then
$$
D=frac{7 {rm cm}}{6.8}=1.02 {rm cm}
$$
is given by
$$
Delta y=2frac{lambda}{d}
$$
So we can see that the width is inversely proportional to the slit
separation $d$. Hence if we increase the slit separation the width
will reduce.
$$
begin{align*}
m &= 1 \
W &= 42 cdot 10^{-5} text{ m} \
lambda &= 625 text{ nm}
end{align*}
$$
The angle to the first-order dark fringe of a light which passes through a single-slit interference can be obtain by applying the expression :
$$
begin{align*}
W sin theta &= m lambda \
sin theta &= dfrac{m lambda}{W} \
theta &= {sin}^{-1} left( dfrac{m lambda}{W} right) \
&= {sin}^{-1} left( dfrac{1 (625 cdot 10^{-9} text{ m})}{42 cdot 10^{-5} text{ m}} right)
end{align*}
$$
$$
{boxed{theta = 0.085 text{textdegree}}}
$$
{theta = 0.085 text{textdegree}}
$$
$$
begin{align*}
m &= 1 \
W &= 2.2 cdot 10^{-6} text{ m} \
theta &= 18 text{textdegree}
end{align*}
$$
The wavelength of the light that passes on a first-order dark fringe in a single-slit interference can be obtain by applying the expression :
$$
begin{align*}
W sin theta &= m lambda \
lambda &= dfrac{W sin theta}{m} \
&= dfrac{2.2 cdot 10^{-6} text{ m} ~ (sin 18 text{textdegree})}{1}
end{align*}
$$
$$
{boxed{lambda = 679.84 text{ nm}}}
$$
{lambda = 679.84 text{ nm}}
$$
$$
begin{align*}
m &= 1 \
theta &= 22 text{textdegree} \
lambda &= 562 text{ nm}
end{align*}
$$
The width of the slit, $W$ , to the first-order dark fringe of light can be obtain by applying the expression :
$$
begin{align*}
W sin theta &= m lambda \
W &= dfrac{m lambda}{sin theta} \
&= dfrac{1 (562 cdot 10^{-9} text{ m})}{sin 22 text{textdegree}}
end{align*}
$$
$$
{boxed{W = 1.5 ~ mu text{m}}}
$$
{W = 1.5 ~ mu text{m}}
$$
$$
begin{align*}
m &= 2 \
theta &= 18.5 text{textdegree} \
lambda &= 632.8 text{ nm}
end{align*}
$$
The width of the slit, $W$ , to the second-order dark fringe of light from a helium-neon laser through a single slit can be obtain by applying the expression :
$$
begin{align*}
W sin theta &= m lambda \
W &= dfrac{m lambda}{sin theta} \
&= dfrac{2 (632.8 cdot 10^{-9} text{ m})}{sin 18.5 text{textdegree}}
end{align*}
$$
$$
{boxed{W = 4 ~ mu text{m}}}
$$
{W = 4 ~ mu text{m}}
$$
$$
begin{align*}
m &= 3 \
W &= 37 cdot 10^{-5} text{ m} \
lambda &= 589 text{ nm}
end{align*}
$$
The angle to the third-order dark fringe of a light which passes through a single-slit interference can be obtain by applying the expression :
$$
begin{align*}
W sin theta &= m lambda \
sin theta &= dfrac{m lambda}{W} \
theta &= {sin}^{-1} left( dfrac{m lambda}{W} right) \
&= {sin}^{-1} left( dfrac{3 (589 cdot 10^{-9} text{ m})}{37 cdot 10^{-5} text{ m}} right)
end{align*}
$$
$$
{boxed{theta = 0.274 text{textdegree}}}
$$
{theta = 0.274 text{textdegree}}
$$
$$
begin{align*}
m &= 1 \
lambda &= 610 text{ nm} \
L &= 2.3 text{ m} \
y &= 12 text{ cm}
end{align*}
$$
Solving for the angle, $theta$ :
$$
begin{align*}
y &= L tan theta \
theta &= {tan}^{-1} left( dfrac{y}{L} right) \
&= {tan}^{-1} left( dfrac{0.12 text{ m}}{2.3 text{ m}} right) \
theta &= 3 text{textdegree}
end{align*}
$$
Now calculating for the width of the slit, $W$ , by applying the expression :
$$
begin{align*}
W sin theta &= m lambda \
W &= dfrac{m lambda}{sin theta} \
&= dfrac{1 (610 cdot 10^{-9} text{ m})}{sin 3 text{textdegree}}
end{align*}
$$
$$
{boxed{W = 11.66 ~ mu text{m}}}
$$
$textbf{(b)}$ $textbf{decrease}$ in value

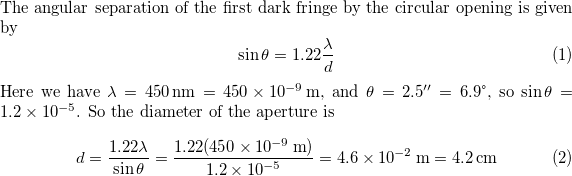


$$
begin{align*}
m &= 1 \
lambda &= 520 text{ nm} \
D &= 0.50 text{ mm} \
y &= 15 text{ cm}
end{align*}
$$
$textbf{(a)}$ The angle to the first-order dark fringe in the diffraction pattern of a pinhole of the camera can be calculated by using the relation for the diffraction pattern of a circular opening :
$$
begin{align*}
sin theta &= 1.22 ~ dfrac{lambda}{D} \
theta &= {sin}^{-1} left( 1.22 ~ dfrac{lambda}{D} right) \
&= {sin}^{-1} left( 1.22 times dfrac{520 cdot 10^{-9} text{ m}}{0.0005 text{ m}}right)
end{align*}
$$
$$
{boxed{theta = 0.0727 text{textdegree}}}
$$
$$
begin{align*}
y &= L tan theta \
L &= dfrac{y}{tan theta} \
&= dfrac{0.15 text{ m}}{(tan 0.0727 text{textdegree})}
end{align*}
$$
$$
{boxed{L = 118.22 text{ m}}}
$$
$textbf{(b)}$ ${L = 118.22 text{ m}}$
$sintheta = frac{lambda}{d}$
So we can see that the $sin$ of the angle is inversely proportional to the line spacing. So if we increase the line spacing the angle of the first order principle maxima will decrease.
$sintheta = frac{lambda}{d}$
So we can see that the $sin$ of the angle is directly proportional to the wavelength of the light. Hence if the wavelength increases the angle of the first order maxima will increase. Since the wavelength of the red light is greater than the blue light, the angle of the first order principle maxima of the red light will be more than the angle of the first order principle maxima of blue light.
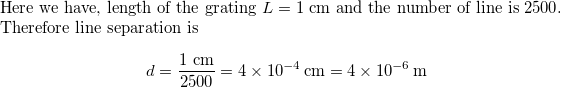
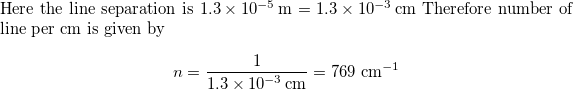
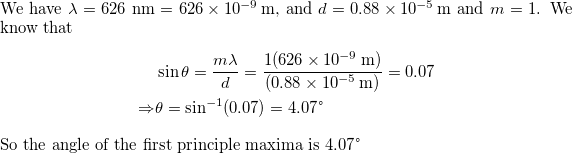
$$
begin{align*}
m &= 1 \
theta &= 24.5 text{textdegree} \
lambda &= 562 text{ nm}
end{align*}
$$
The split spacing for the diffraction grating to the first order principal maximum of the light can be obtain by applying the expression for constructive interference by a diffraction grating :
$$
begin{align*}
d sin theta &= m lambda \
d &= dfrac{m lambda}{sin theta} \
&= dfrac{1 (562 cdot 10^{-9} text{ m})}{(sin 24.5 text{textdegree})}
end{align*}
$$
$$
{boxed{d = 1.36 ~ mu text{m}}}
$$
{d = 1.36 ~ mu text{m}}
$$
$$
begin{align*}
m &= 2 \
d &= 2.7 ~ mu text{m} \
theta &= 43 text{textdegree}
end{align*}
$$
The wavelength of the light that passes on a diffraction grating through an angle to the second-order principal maximum can be obtain by applying the expression for constructive interference by a diffraction grating :
$$
begin{align*}
d sin theta &= m lambda \
lambda &= dfrac{d sin theta}{m} \
&= dfrac{2.7 cdot 10^{-6} text{ m} ~ (sin 43 text{textdegree})}{2}
end{align*}
$$
$$
{boxed{lambda = 920.7 text{ nm}}}
$$
{lambda = 920.7 text{ nm}}
$$
$$
begin{align*}
m &= 3 \
d &= 1.3 cdot 10^{-5} text{ m} \
lambda &= 426 text{ nm}
end{align*}
$$
The angle to the third-order principal maximum of a light on a diffraction grating can be obtain by applying the expression for constructive interference by a diffraction grating :
$$
begin{align*}
d sin theta &= m lambda \
sin theta &= dfrac{m lambda}{d} \
theta &= {sin}^{-1} left( dfrac{m lambda}{d} right) \
&= {sin}^{-1} left( dfrac{3 (426 cdot 10^{-9} text{ m})}{1.3 cdot 10^{-5} text{ m}} right)
end{align*}
$$
$$
{boxed{theta = 5.64 text{textdegree}}}
$$
{theta = 5.64 text{textdegree}}
$$
$$
begin{align*}
m &= 2 \
d &= 1.8 cdot 10^{-5} text{ m} \
theta &= 3.1 text{textdegree}
end{align*}
$$
$textbf{(a)}$ The wavelength of the light that shines on a diffraction grating through an angle to the second-order principal maximum can be obtain by applying the expression for constructive interference by a diffraction grating :
$$
begin{align*}
d sin theta &= m lambda \
lambda &= dfrac{d sin theta}{m} \
&= dfrac{1.8 cdot 10^{-5} text{ m} ~ (sin 3.1 text{textdegree})}{2}
end{align*}
$$
$$
{boxed{lambda = 486.71 text{ nm}}}
$$
$textbf{(b)}$ $textbf{greater than}$ $3.1 text{textdegree}$


$$
sintheta = frac{mlambda}{d}
$$
So we can see that $sintheta$ is inversely proportional to the slit width $d$.
This means that if the slit width is decreased, the angle will increase. Hence the consecutive dark fringe will go farther away from each other.
$$
theta=1.22frac{lambda}{d}
$$
Now we can see that the angle decreases if we increase the diamtere
($d$) of the aperture. This means if we increase the size of the
pupil the angle that we can resolve will decrease, that is resolution
will increase.
line spacing of a grating is given by
$$
sintheta=frac{mlambda}{d}
$$
So we can see that if the line spacing decreases, the angle of the
principal maxima increases. Hence the seperation between the principle
maxima will increase. Now if we increase the number of line per centimeter
in the grating, we are actually decreasing the line spacing. Hence,
if we increase the number of line per centimeter, the principal maxima
will move further.
$$
begin{align*}
m &= 2 \
d &= 12 cdot 10^{-5} text{ m} \
lambda &= 561 text{ nm}
end{align*}
$$
The angle of the light to the second-order bright fringe above the central bright fringe can be calculated by using the expression for conditions for bright fringes in a two-slit experiment :
$$
begin{align*}
d sin theta &= m lambda \
sin theta &= dfrac{m lambda}{d} \
theta &= {sin}^{-1} left( dfrac{m lambda}{d} right) \
&= {sin}^{-1} left( dfrac{2 (561 cdot 10^{-9} text{ m})}{12 cdot 10^{-5} text{ m}} right)
end{align*}
$$
$$
{boxed{theta = 0.536 text{textdegree}}}
$$
{theta = 0.536 text{textdegree}}
$$
A. The film will appear bright because as its thickness goes to zero, the path-length difference for the reflected rays goes to zero.
$$
begin{align*}
m &= 1 \
lambda &= 589 text{ nm} \
L &= 1.3 text{ m} \
W &= 9.7 cdot 10^{-5} text{ m}
end{align*}
$$
Solving for the angle, $theta$ , by applying the expression :
$$
begin{align*}
W sin theta &= m lambda \
sin theta &= dfrac{m lambda}{W} \
theta &= {sin}^{-1} left( dfrac{m lambda}{W} right) \
&= {sin}^{-1} left( dfrac{1 (589 cdot 10^{-9} text{ m})}{9.7 cdot 10^{-5} text{ m}} right) \
theta &= 0.348 text{textdegree}
end{align*}
$$
Solving for the linear distance, $y$ , by applying the expression for linear distance from the central bright fringe:
$$
begin{align*}
y &= L tan theta \
&= 1.3 text{ m} ~ (tan 0.348 text{textdegree})
end{align*}
$$
$$
{boxed{y = 7.9 text{ mm}}}
$$
{y = 7.9 text{ mm}}
$$
$$
begin{align*}
m &= 2 \
y &= 15.2 text{ cm} \
L &= 0.865 text{ m} \
W &= 11.2 cdot 10^{-6} text{ m}
end{align*}
$$
Solving for the angle, $theta$ :
$$
begin{align*}
dfrac{y}{2} &= L tan theta \
theta &= {tan}^{-1} left( dfrac{y}{2 L} right) \
&= {tan}^{-1} left( dfrac{0.152 text{ m}}{2 times 0.865 text{ m}} right) \
theta &= 5.02 text{textdegree}
end{align*}
$$
Now calculating for the wavelength, $lambda$ , by applying the expression :
$$
begin{align*}
W sin theta &= m lambda \
lambda &= dfrac{W sin theta}{m} \
&= dfrac{11.2 cdot 10^{-6} text{ m} ~ (sin 5.02 text{textdegree})}{2}
end{align*}
$$
$$
{boxed{lambda = 490 text{ nm}}}
$$
$textbf{(b)}$ $textbf{greater than}$ $15.2 text{ cm}$
$$
begin{align*}
m &= 1 \
lambda &= 474 text{ nm} \
D &= 5.5 text{ mm}
end{align*}
$$
The minimum angle to the first-order dark fringe in the diffraction pattern of the eye can be calculated by using the relation for the diffraction pattern of a circular opening :
$$
begin{align*}
sin theta &= 1.22 ~ dfrac{lambda}{D} \
theta &= {sin}^{-1} left( 1.22 ~ dfrac{lambda}{D} right) \
&= {sin}^{-1} left( 1.22 times dfrac{474 cdot 10^{-9} text{ m}}{0.0055 text{ m}}right)
end{align*}
$$
$$
{boxed{theta = 6.02 cdot 10^{-3}}}
$$
$$
begin{align*}
h &= 39.9 text{ cm} \
N &= 1080
end{align*}
$$
The linear separation between the horizontal lines on the screen is equal to the height of the TV screen divided by the number of horizontal lines :
$$
{d = dfrac{h}{N}}
$$
$$
{d = dfrac{399 text{ mm}}{1080}}
$$
$$
{boxed{d = 0.369 text{ mm}}}
$$
The distance from the screen is $D=3.66 {rm m}$
Hence the angular separation is
$$
begin{align*}
theta & = frac{y}{D}\
& = frac{0.0369times 10^{-2} {rm m}}{3.66 {rm m}}\
& = 1.00times 10^{-4} {rm rad}\
& = 5.78times 10^{-3} {rm degree}
end{align*}
$$

