
All Solutions
Page 698: Assessment
Reason- When a neutral object become charged,only the charge transfer takes place between the two bodies, ie. the neutral body and the charged body that is supplying the charge. But the total charge of the universe remains constant .
$textbf{(b)}$ The best explanation is
$textbf{A.}$ To give an object a negative charge requires giving it more electrons, which will increase its mass.
$textbf{(b)}$ If the charge on the balloon is reversed, the stream of water will deflect still $toward$ the balloon, because the neutral water is attracted to the charged balloon due to the effect of $polariziation$, which gives rise to an attractive force regardless of the sign of the charged object.
$textbf{(b)}$ From Table 19.1 Glass has a $positive$ triboelectric charging relative to Rubber. As a result, if glass is rubbed against rubber, we end up with glass acquiring a positive charge and rubber acquiring a negative charge.
$textbf{(c)}$ As we see in Table 19.1, the difference in relative triboelectric charging is greater in the case in part (b), in which case the magnitude of the charge is greater.
$textbf{(b)}$ glass is positive, rubber is negative
$textbf{(c)}$ (b)
$$
begin{align*}
2;mathrm{moles}&left(frac{6.022times10^{23};mathrm{atoms}}{rm mole}right)left(frac{6;mathrm{protons}}{rm atom}right)left(frac{1.60times10^{-19};mathrm{C}}{rm proton}right)\
&= 1.16times10^6;mathrm{C}
end{align*}
$$
$$
212(-e) + 165(e) = -47e = -47(1.60times10^{-19};mathrm{C}) = -7.52times10^{-18};mathrm{C}
$$
The total chare of the system is negative and has a magnitude of $7.52times10^{-18}$ C.
-7.52times10^{-18};mathrm{C}
$$
$$
begin{align*}
1.5;mathrm{kg}&left(frac{rm electron}{9.11times10^{-31};mathrm{kg}}right)left(frac{-1.60times10^{-19};mathrm{C}}{rm electron}right)\
&= -2.6times10^{11};mathrm{C}
end{align*}
$$
-2.6times10^{11};mathrm{C}
$$
$$
begin{align*}
1.5;mathrm{kg}&left(frac{rm electron}{1.67times10^{-27};mathrm{kg}}right)left(frac{1.60times10^{-19};mathrm{C}}{rm electron}right)\
&= 1.4times10^{8};mathrm{C}
end{align*}
$$
1.4times10^{8};mathrm{C}
$$
$$
n(-e) + 150(e) = -35e ;;Rightarrow;; -n + 150 = -35
$$
where we used the fact that each electron has $-e$ charge and each proton has $+e$ charge. Solving for $n$ gives us $n = 185$. Since the masses of neutron and proton are almost the same and equal to $m_napprox m_p = 1.67times10^{-27}$ kg and the mass of electron is $m_e = 9.11times10^{-31}$ kg, the total mass of the system is
$$
begin{align*}
250m_n + 150m_p + 185m_e &= (250 + 150)(1.67times10^{-27};mathrm{kg}) + 185(9.11times10^{-31};mathrm{kg})\
&= 6.68times10^{-25};mathrm{kg}
end{align*}
$$
$$
1.75;mathrm{moles}left(frac{6.022times10^{23};mathrm{molecules}}{rm moole}right) approx 10^{24};mathrm{molecules}
$$
Since one in a million of these molecules acquires a positive chare of magnitude $e$, the total charge of the gas is
$$
10^{24};mathrm{molecules}timesfrac{1}{10^6}timesfrac{1.60times10^{-19};mathrm{C}}{rm molecule} = 0.16;mathrm{C}
$$
Absolute value of the charge of an electron is $|q| = 1.6 times 10^{-19} :C$.
So the tape transfers, $dfrac{0.14 times 10^{-6}}{1.6 times 10^{-19}} = 8.75 times 10^{11}:electrons/cm$
The length of the tape to be pulled to transfer $1.8 times 10^{13}:electrons$ is
$dfrac{1.8 times 10^{13}}{8.75 times 10^{11}} =20.6:cm$
20.6:cm
$$
Charge of the proton is $+1.6 times 10^{-19}:C$.
So in a system containing electrons and protons, the charge of the electron is compensated by the charge of the proton.
Total number of particles of the given system is 1525.
Total charge of the given system is $Q = -5.456 times 10^{-17}:C$
So the number of uncompensated electrons of the system is
$dfrac{-5.456 times 10^{-17}}{-1.6 times 10^{-19}} = 341$.
The remaining $1525 – 341 = 1184$ particles must contain equal number of protons and electrons.
So the number of compensated electrons is $dfrac{1184}{2} = 592$.
(b) The system consists of 592 protons and 933 electrons.
Mass of a proton is $1.673 times 10^{-27}:kg$.
Mass of an electron is $9.11 times 10^{-31};kg$.
Total mass ($M$) of the system is
$M = (592 times 1.673 times 10^{-27}) + (933 times 9.11 times 10^{-31}):kg$
$$
M = 9.91times10^{-25};mathrm{kg}
$$
(b) $M = 9.91times10^{-25};mathrm{kg}$
Charge of an electron is $-1.6 times 10^{-19}:C$.
In a system consisting of electrons and protons, the charge of the protons is compensated by the charge of the electrons.
Total charge of the given system is $Q =2.4 times 10^{-16}:C$.
So the number of uncompensated protons in the system is
$dfrac{2.4 times 10^{-16}}{1.6 times 10^{-19}} = 1500$.
Mass of a proton is $1.673 times 10^{-27}:kg$.
So mass of uncompensated protons is, $1500 times 1.673 times 10^{-27} =2.51 times 10^{-24}:kg$.
The remaining mass $(4.5 – 2.51) times 10^{-24} = 2.01 times 10^{-24}:kg$ of the system consists of equal number of protons and electrons.
Say $n$ is that number. Then we have the following equation.
$(n times m_e) + (n times m_p) = n (m_e + m_p) = 2.01 times 10^{-24}:kg$
where $m_e = 0.00091 times 10^{-27}:kg$ is the mass of the electron and $m_p = 1.673 times 10^{-27} :kg$ is the mass of the proton.
Then,
$n (0.00091 times 10^{-27} + 1.673 times 10^{-27}) = 2.01 times 10^{-24}$
$n times 1.67391 times 10^{-27} = 2.01 times 10^{-24} :kg$
$n = dfrac{2.01 times 10^{-24}}{1.67391 times 10^{-27}} = 1201$
So the system consists of 1201 electrons and $1201 + 1500 = 1701$ protons.
$r = sqrt{dfrac{k |q_1| |q_2|}{F}}:m$
where $k$ is proportionality constant.
For system A,
$r_A = sqrt{dfrac{k times 16 times 3}{3}} = 4 sqrt{k}:m$
For system B,
$r_B = sqrt{dfrac{k times 2 times 4}{2}} = 2 sqrt{k}:m$
For system C,
$r_C = sqrt{dfrac{k times 5 times 5}{5}} = sqrt{5 k}:m = 2.23 sqrt{k}:m$
For system D,
$r_D = sqrt{dfrac{k times 1times 2}{2}} = sqrt{k} :m$
So,
$r_D: text{textless} : r_B : text{textless} : : r_C : text{textless} : r_A$
D<B<C<A
$$
$F = k dfrac{|q_1| |q_2|}{d^2}$
where $k$ is constant.
So the electric force depends on the product of the absolute values of the charges and the square of the separation between them.
In both case 1 and case 2, the absolute value of the charges and separation between them is same.
Hence the magnitude of the force exerted on the charge in the origin is same in both case 1 and case 2. Only the direction of force changes.
In case 1, both charges are of same kind. Hence the force is repulsive and force on $q$ acts to the left.
In case 2, both charges are of opposite kind. So the force is attractive and the force on $q$ acts to the right.
electric force the physical quantity is the charge; for gravity it is the mass.
Dissimilarities- For example, the force of gravity is always attractive, whereas the electric force can be attractive or repulsive.
$F = k dfrac{|q_1| |q_2|}{r^2}$
where $k = 8.99 times 10^9: N.m^2. C^{-2}$.
The value of charges are given as $q_1 = 0.12:C$ and $q_2 = 0.33:C$.
The separation between them is $r =2.5:m$.
So,
$F = dfrac{8.99 times 10^9 times 0.12 times 0.33}{2.5^2} = dfrac{8.99 times 0.12 times 0.33}{2.5^2} times 10^9 = 57 times 10^6:N$
Since both charges are of same kind, the force is repulsive.
$F = k dfrac{|q|^2}{r^2}$
where $k = 8.99 times 10^9:N.m^2.C^{-2}$
This relation can be rewritten for the magnitude of the charge as
$|q| = sqrt{dfrac{F}{k}} times r$
The magnitude of the force is given as $F = 1.9:N$ and the separation is given as $r=1.2:m$
So, $|q| = sqrt{dfrac{1.9}{8.99 times 10^9}} times 1.2 = sqrt{2.1135} times 1.2 times 10^{-4} = 17;mumathrm{C}$
17;mumathrm{C}
$$
$F = k dfrac{|q_1| |q_2|}{r^2}$
where $k=8.99 times 10^9 :N.m^2.C^{-2}$
Given data are,
$F=0.975:N$; $q_1 = +8.44 times 10^{-6}:C$; $q_2 = Q:C$ and $r=1.31:m$
Substituting these values,
$0.975 = dfrac{8.99 times 10^9 times 8.44 times 10^{-6} times |Q|}{1.31^2} = dfrac{75875.6 times |Q|}{1.7161} = 44213.97 times |Q|$
So, $|Q| = dfrac{0.975}{44213.97} =-22.1;mumathrm{C}$
Since the force is attractive and $q_1$ is positive charge, $Q$ must be a negative charge.
So, $Q = – 22.1;mumathrm{C}$
Q = 22.1;mumathrm{C}
$$
Then force of $q_1$ due to $q_2$ when they are separated by a distance of $r=0.255:m$ is given by
$F_{12} = k dfrac{|q_1| |q_2|} {r^2}$
where $k = 8.99 times 10^9 :N.m^2. C^{-2}$
Substituting the values,
$F_{12}=dfrac{8.99 times 10^9 times 3.13 times 10^{-6} times 4.47 times 10^{-6}}{0.255^2} = dfrac{8.99 times 3.13 times 4.47}{0.255^2} times 10^{-3}$
$F_{12} =1.934 :N$
(b) The magnitude of the force on $q_2$ due to $q_1$ at separation of $r$ is given by
$F_{21} = k dfrac{|q_1| |q_2|}{r^2}$
This is same as $F_{12}$. But the direction of $F_{21}$ is opposite to that of $F_{12}$. That is,
$vec{F}_{12} = – vec{F}_{21}$.
(b) Same; Newton’s third law
$F = k dfrac{|q_1| |q_2|}{r^2}$
where $k = 8.99 times 10^9:N.m^2.C^{-2}$
This relation can be rewritten for the separation between the charges as
$r = sqrt{dfrac{k |q_1| |q_2|}{F}}$
Given data are,
$q_1 = 2.1 times 10^{-6}:C$; $q_2 = 5.0 times 10^{-6}:C$; $F = 0.25:N$
So, $r = sqrt{dfrac{8.99 times 10^9 times 2.1 times 10^{-6} times 5.0 times 10^{-6}}{0.25}}= sqrt{dfrac{8.99 times 2.1 times 5.0 times 10^{-3}}{0.25}}$
$r=sqrt{0.37758} approx 0.61:m$
r = 0.61 text{m}
$$
Charge of two electrons is $2 times (-1.6 times 10^{-19}) = -3.2 times 10^{-19}:C$.
Since the ion is missing two electrons its magnitude of charge is same as that of two electrons but its polarity is opposite to that of two electrons. So the charge of two identical ions is
$q_1 = q_2 = +3.2 times 10^{-19}:C$
The separation between them is given as
$r = 2.1 times 10^{-10}:m$
The magnitude of the force between them is
$F = dfrac{8.99 times 10^9 times (3.2 times 10^{-19})^2}{(2.1 times 10^{-10})^2}$
where $8.99 times 10^9$ is a proportionality constant with unit $N.m^2.C^{-2}$.
$F = dfrac{8.99 times (3.2)^2 times 10^9 times 10^{-38}}{(2.1)^2 times 10^{-20}} = dfrac{8.99 times 10.24}{4.41} times 10^9 times 10^{-38} times 10^{20}$
$F = 20.87 times 10^{-9}:N$
F = 21times10^{-9} text{N}
$$
$F_{electric} = k dfrac{e^2}{r^2}$
where $e = 1.6 times 10^{-19}:C$ and $k = 8.99 times 10^9 :N.m^2.C^{-2}$ and $r$ is the separation between proton and electron or the radius of the orbit of the electron.
The centripetal force acting on the circulating electron is given by
$F_{centripetal} = dfrac{m_e v^2}{r}$
where $m_e = 9.11 times 10^{-31}:kg$ is the mass of the electron and $v = 7.3 times 10^5:m/s$ is the speed of the electron.
According to Bohr’s model, the centripetal force on the electron is given by the electric force between the proton and the electron. So we have
$dfrac{ke^2}{r^2} = dfrac{m_e v^2}{r}$; This can be rewritten as
$dfrac{ke^2}{m_e v^2} = dfrac{r^{cancel{2}}}{cancel{r}}$ or
$r = dfrac{ke^2}{m_e v^2}$; Substituting the values,
$r = dfrac{8.99 times 10^9 times (1.6 times 10^{-19})^2}{9.11 times 10^{-31} times (7.3 times 10^5)^2} = dfrac{8.99 times 1.6^2}{9.11 times 7.3^2} times 10^9 times 10^{-38} times 10^{31} times 10^{-10}$
$r = 4.7 times 10^{-10}:m = 4.7 :A^o$
r = 4.7; A^circ
$$
Mass of the electron is, $m_e = 9.11 times 10^{-31}:kg$.
So the weight of the electron is, $m_e g = 9.11 times 10^{-31} times 9.8 = 89.28 times 10^{-31}: N$
Suppose an electron is placed at distance $r$ above a charge $q= -0.51 times 10^{-9}:C$. The magnitude of the electric force between them is given by
$F=k dfrac{|q| |e|}{r^2} = dfrac{8.99 times 10^9 times 0.51 times 10^{-9} times 1.6 times 10^{-19}}{r^2} = dfrac{7.34 times 10^{-19}}{r^2}:N$
This force is repulsive because both charges are of same kind. It pushes the electron above. But the weight of the electron acts downwards. So both forces are opposite to each other.
Both forces are exactly opposite only if their magnitudes are same.
The separation $r$ at which the magnitude of the both forces become equal can be found by equating both forces.
$89.28 times 10^{-31} = dfrac{7.34 times 10^{-19}}{r^2}$
$r^2 = dfrac{7.34 times 10^{-19}}{89.28 times 10^{-31}} = 8.22 times 10^{10};m^2$
So, $r = sqrt{8.22 times 10^{10}} = 286.71 times 10^3:m = 286.71:km$
So the electron has to be placed $286.71:km$ above the charge $-0.51:nC$ for the electric force on electron to be exactly opposite to its weight.
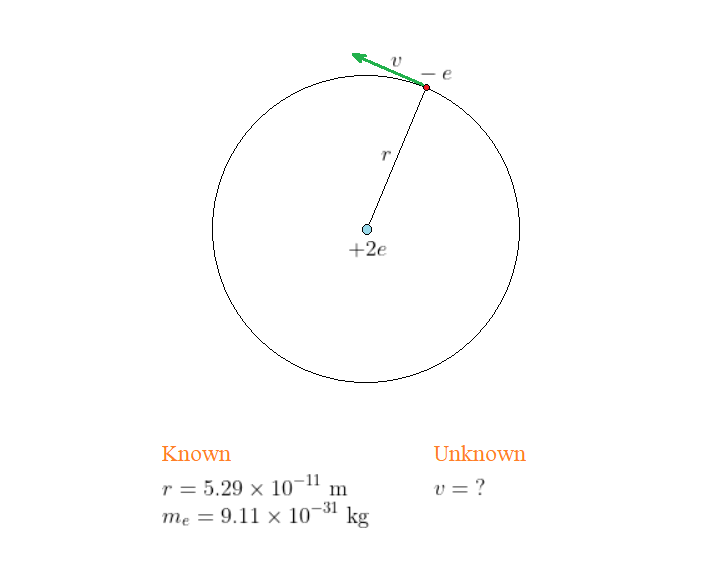
$textbf{(b)}$ $text{color{#4257b2}Picture the Problem}$
Our sketch shows the electron moving with a speed $v$ in its orbit of radius $r$. Because the nucleus is so much more massive than the electron, it is essentially stationary at the center of the orbit. The electron has the charge $-e$ and the nucleus has the charge $+2e$.
$text{color{#4257b2}Strategy}$
The electrical force acting on the
electron due to the nucleus is equal to its mass times its centripetal acceleration. This allows us to solve for the centripetal acceleration, $a_{rm cp} = v^2 / r$, which in turn gives us the speed, $v$.
$text{color{#4257b2}Solution}$
Set the Coulomb force between the electron and the nucleus equal to the centripetal force required for the electron’s circular orbit. Then, substitute $e$ and $2e$ for the magnitude of charges and $v^2/r$ for $a_{rm cp}$:
$$
begin{align*}
kfrac{|q_1||q_2|}{r^2} &= m_ea_{rm cp}\
kfrac{2e^2}{r^2} &= m_efrac{v^2}{r}
end{align*}
$$
Solve for the speed of the electron, $v$:
$$
v = esqrt{frac{2k}{m_er}}
$$
Substitute the known values and calculate $v$ (recall that 1 N = 1 kg $cdot$ m/s$^2$):
$$
begin{align*}
v &= (1.60times10^{-19};mathrm{C})timessqrt{frac{2(8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2)}{(9.11times10^{-31};mathrm{kg})(5.29times10^{-11};mathrm{m})}}\
&= 3.09times10^6;mathrm{m/s}
end{align*}
$$
which is, indeed, greater than that found in the guided example.
$$
kfrac{q_1q_2}{r^2} = F
$$
Solving for the product $q_1q_2$ and substituting the known values, we find
$$
q_1q_2 = frac{Fr^2}{k} = frac{(75.0;mathrm{N})(0.270;mathrm{m})^2}{8.99times10^{9};mathrm{N}cdotmathrm{m}^2/mathrm{C}^2} = 608;mu^2mathrm{C}^2
$$
Moreover, the two charges have a total magnitude of
$$
Q = q_1 + q_2 = 62.0;mumathrm{C}
$$
Solving the latter equation for $q_2$ and substituting the result into the former, we have
$$
q_1(62.0;mumathrm{C} – q_1) = 608;,mu^2mathrm{C}^2
$$
Rearranging the equation gives us the following quadratic equation in $q_1$:
$$
q_1^2 – (62.0;mumathrm{C})q_1 + 608;mu^2mathrm{C}^2 = 0
$$
which has the two solutions $q_1 = 49.8;mu$C or $12.2;mu$C. Correspondingly, the value of $q_2$ is $12.2;mu$C or $49.8;mu$C.
$F = dfrac{k |q|^2}{r^2}$
where $k = 8.99 times 10^9:N.m^2.C^{-2}$.
Since both charges are identical the force between them is repulsive. The string connecting them is expanded. Tension on the string is $0.21:N$. Length of the string or the separation between the charges is $7.6:cm = 0.076:m$.
$|q|^2 = dfrac{F r^2}{k} = dfrac{0.21 times 0.076^2}{8.99 times 10^9} =0.1349 times 10^{-12}:C^2$
$|q| = sqrt{0.1349 times 10^{-12}} = 0.367 times 10^{-6}:C = 0.367:mu C$
(b) We cannot determine the sign of the charges from the given information. Since both charges are identical, the force is always repulsive irrespective of the sign of the charges.
From the magnitude of the force and separation between them, we can find only the magnitude of the charges.
If $+1.0 : mu C$ is transferred from one point charge to another point charge, then the magnitude of one charge becomes $(1 + 0.367):mu C$ and of another becomes $(1-0.367):mu C$.
Say, $|q_1| = 1.367 :mu C$ and $|q_2| = 0.633:mu C$.
The magnitude of the force is
$F = dfrac{k |q_1||q_2|}{r^2} = dfrac{8.99 times 10^9 times 1.367 times 10^{-6} times 0.633 times 10^{-6}}{0.073^2} = 1.46:N$
Since $0.367 :mu C : text{textless} : 1 :mu C$, transfer of $+1 :mu C$ charge creates additional charges. As a result the magnitude of the force has increased.
The charges are of opposite kind.
That is,
if $q = +0.367:mu C$ then $q_1 = -0.633 : mu C$ and $q_2 = 1.367:mu C$.
if $q = -0.367:mu C$ then $q_1 = -1.367 : mu C$ and $q_2 = -0.633:mu C$.
so the force is attractive and the string is shrunk.
(b) no; the force between the identical charges is repulsive, irrespective of the signs of the charges
(c) zero; unlike the case in (a) this time the force is attractive, for which the string gets loosely and the tension in it vanishes
Second, consider the forces acting on charge B, as shown in Fig. 1b. There are two forces acting on charge B due to charges A and C. The two attractive forces are equal in magnitude and opposite in direction; the positive charge B is halfway between the negative charges A and C. Thus the total force experienced by charge B has a zero magnitude.
Third, consider the forces acting on charge C, as shown in Fig. 1c. There are two forces acting on charge C due to charges A and B, which are different in magnitude and opposite in direction. The magnitude of the attractive force due to B is $F$. Since the charge A is $2d$ distance from C, the magnitude of the repulsive force due to A is $F/4$. As a result, the total force experienced by charge C has the magnitude $3F/4$. (The fact that the results for charges A and C are the same isn’t a surprise because the problem is symmetric about charge B).
We see the total force on B is the smallest in magnitude (zero), then come the total forces on charges A and C, which have the same magnitude $3F/4$.
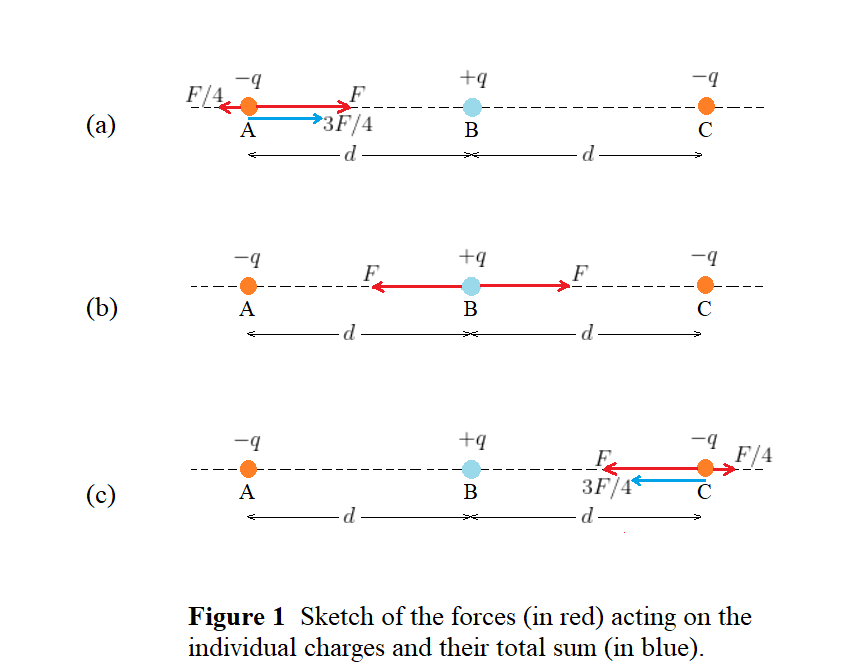
rm B < A = C
$$
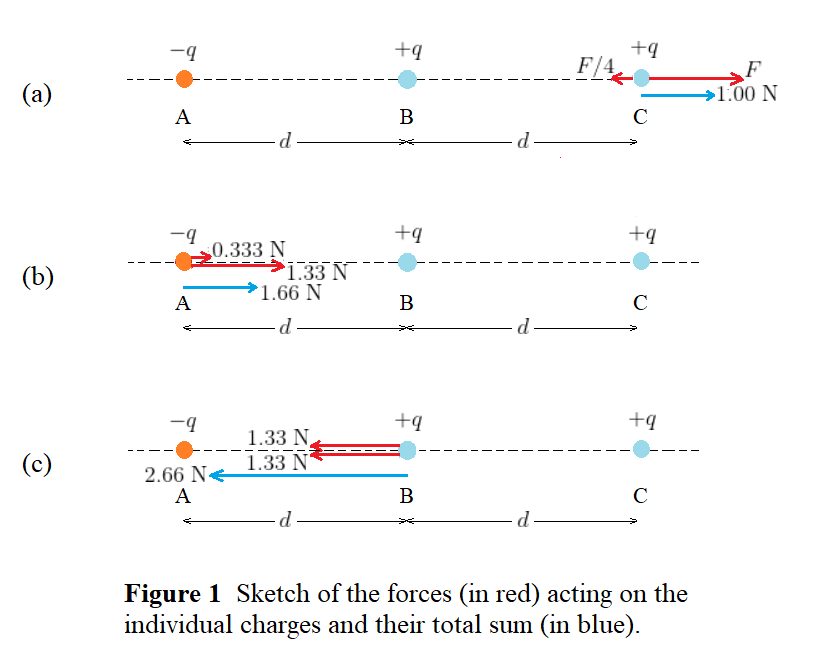
$textbf{(a)}$ Consider the forces acting on charge A, as shown in Fig. 1b. There are two forces acting on charge A due to charges B and C, which have the same direction and different magnitudes. The magnitude of the attractive force due to B (a distance $d$ from A) is $F = 1.33$ N. The charge C is $2d$ distance from A, so the magnitude of the force due to C is $F/4 = 0.333$ N. Thus the total force experienced by charge A has a magnitude of 1.33 N + 0.333 N = 1.66 N.
$textbf{(b)}$ Consider the forces acting on charge B, as shown in Fig. 1c. There are two forces acting on charge B due to charges A and C, which have the same direction and magnitude. The magnitude of the attractive force due to A (a distance $d$ from B) is $F = 1.33$ N. The magnitude of the repulsive force due to C (a distance $d$ from B) is also $F = 1.33$ N. Thus the total force experienced by charge B has a magnitude 1.33 N + 1.33 N = 2.66 N.
Consider charge 1, which has the magnitude $|q_1| = q$. There are two repulsive forces acting on charge 1. The first is due to charge 2 and is proportional to the product $|q_1||q_2| = 2q^2$, and the second is due to charge 3 and is proportional to the product $|q_1||q_3| = 3q^2$. By the symmetry of the equilateral triangle, the two forces are directed in such a way the angle between them is $60^circ$. The total force experienced by charge 1 is the vector sum of the two forces with magnitudes proportional to $2q^2$ and $3q^2$, and angular separation of $60^circ$.
Consider charge 2, which has the magnitude $|q_2| = 2q$. There are two repulsive forces acting on charge 2. The first is due to charge 1 and is proportional to the product $|q_2||q_1| = 2q^2$, and the second is due to charge 3 and is proportional to the product $|q_2||q_3| = 6q^2$. By the symmetry of the equilateral triangle, the two forces are directed in such a way the angle between them is $60^circ$. The total force experienced by charge 2 is the vector sum of the two forces with magnitudes proportional to $2q^2$ and $6q^2$, and the $same$ angular separation of $60^circ$.
Consider charge 3, which has the magnitude $|q_3| = 3q$. There are two repulsive forces acting on charge 3. The first is due to charge 1 and is proportional to the product $|q_3||q_1| = 3q^2$, and the second is due to charge 2 and is proportional to the product $|q_3||q_2| = 6q^2$. By the symmetry of the equilateral triangle, the two forces are directed in such a way the angle between them is $60^circ$. The total force experienced by charge 3 is the vector sum of the two forces with magnitudes proportional to $3q^2$ and $6q^2$, and the $same$ angular separation of $60^circ$.
We see $textbf{(a)}$ charge 3 experiences the greatest total force and $textbf{(b)}$ charge 1 experiences the smallest total force.
Surface charge density of the sphere is, $sigma = +7.1 :dfrac{mu C}{m^2}$.
So the total charge on the sphere is, $Q = sigma A = +7.1:dfrac{mu C}{cancel{m^2}} times 0.42 :cancel{m^2} = +2.982 :mu C$.
This sphere of total charge $+2.982:mu C$ can be considered as point charge $Q = +2.982:mu C$ located at the center of the sphere.
The magnitude force between the sphere and a point charge $q=-6.6:mu C$ located at a separation of $r=0.68;m$ from the center of the sphere is given by
$F = k dfrac{|Q| |q|}{r^2}$
where $k = 8.99 times 10^9:N.m^2.C^{-2}$. Substituting the values,
$F = dfrac{8.99 times 10^9 times 2.982 times 10^{-6} times 6.6 times 10^{-6}}{(0.68)^2} = dfrac{8.99 times 2.982 times 6.6}{0.4624} times 10^{-3}$
$$
F =0.383:N
$$
{color{#4257b2}text{Picture the Problem}}
$$
The situation is shown in our sketch, with each charge at its appropriate location. Notice that the forces exerted on charge 1 (with charge $q_1$) by the charges 2 and 3 (with charges $q_2$ and $q_3$ respectively) are in opposite directions. We give the force on $q_1$ due to $q_2$ the label $vec{pmb F}_{12}$ and the force on $q_1$ due to $q_3$ the label $vec{pmb F}_{13}$.
$$
{color{#4257b2}text{Strategy}}
$$
The total force on $q_1$, denoted by $vec{pmb F}_1$, is the vector sum of the forces due to $q_2$ and $q_3$. In particular, notice that $vec{pmb F}_{12}$ points in the positive $x$ direction and $vec{pmb F}_{13}$ points in the negative $x$ direction. The magnitude of $vec{pmb F}_{12}$ is $k|q_1||q_2|/r^2$, with $r = 7.5$ cm = 0.075 m. Similarly, the magnitude of $vec{pmb F}_{13}$ is $k|q_1||q_3|/r^2$, with $r = 11$ cm = 0.11 m.

{color{#4257b2}text{Solution}}
$$
$$
begin{align*}
vec{pmb F}_{12} &= +kfrac{|q_1||q_2|}{r^2}\
&= +(8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2)timesfrac{(2.1times10^{-6};mathrm{C})(3.2times10^{-6};mathrm{C})}{(0.075;mathrm{m})^2}\
&= 11;mathrm{N}qquad(text{positive};x;text{direction})\
vec{pmb F}_{32} &= -kfrac{|q_2||q_3|}{r^2}\
&= -(8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2)timesfrac{(2.1times10^{-6};mathrm{C})(1.8times10^{-6};mathrm{C})}{(0.11;mathrm{m})^2}\
&= -2.8;mathrm{N}qquad(text{negative};x;text{direction})\
vec{pmb F}_1 &= vec{pmb F}_{12} + vec{pmb F}_{13}\
&= 10;mathrm{N} – 2.8;mathrm{N}\
&= 7.2;mathrm{N}qquad(text{positive};x;text{direction})
end{align*}
$$
$$
{color{#4257b2}text{Insight}}
$$
The total force exerted on charge 1 has the magnitude of 7.2 N, and it points in the positive $x$ direction. Notice that the force due to $q_2$ is much greater than that due to $q_3$. The reason is that the charge $q_2$ has a magnitude that is about 1.8 times that of $q_2$ and it is also about one and a half times closer to $q_1$ than $q_3$ is.
{color{#4257b2}text{Picture the Problem}}
$$
The situation is shown in our sketch, with each charge at its appropriate location. Notice that the forces exerted on charge 2 (with charge $q_2$) by the charges 1 and 3 (with charges $q_1$ and $q_3$ respectively) are in opposite directions. We give the force on $q_2$ due to $q_1$ the label $vec{pmb F}_{21}$ and the force on $q_2$ due to $q_3$ the label $vec{pmb F}_{23}$.
$$
{color{#4257b2}text{Strategy}}
$$
The total force on $q_2$, denoted by $vec{pmb F}_2$, is the vector sum of the forces due to $q_1$ and $q_3$. In particular, notice that $vec{pmb F}_{21}$ points in the negative $x$ direction and $vec{pmb F}_{23}$ points in the positive $x$ direction. The magnitude of $vec{pmb F}_{21}$ is $k|q_2||q_1|/r^2$, with $r = 7.5$ cm = 0.075 m. Similarly, the magnitude of $vec{pmb F}_{23}$ is $k|q_2||q_3|/r^2$, with $r = 3.5$ cm = 0.035 m.

{color{#4257b2}text{Solution}}
$$
$$
begin{align*}
vec{pmb F}_{21} &= -kfrac{|q_2||q_1|}{r^2}\
&= -(8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2)timesfrac{(3.2times10^{-6};mathrm{C})(2.1times10^{-6};mathrm{C})}{(0.075;mathrm{m})^2}\
&= -11;mathrm{N}qquad(text{negative};x;text{direction})\
vec{pmb F}_{23} &= +kfrac{|q_2||q_3|}{r^2}\
&= +(8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2)timesfrac{(3.2times10^{-6};mathrm{C})(1.8times10^{-6};mathrm{C})}{(0.0.35;mathrm{m})^2}\
&= +42;mathrm{N}qquad(text{positive};x;text{direction})\
vec{pmb F}_2 &= vec{pmb F}_{21} + vec{pmb F}_{23}\
&= -11;mathrm{N} + 42;mathrm{N}\
&= +31;mathrm{N}qquad(text{positive};x;text{direction})
end{align*}
$$
$$
{color{#4257b2}text{Insight}}
$$
The total force exerted on charge 2 has the magnitude of 31 N, and it points in the positive $x$ direction. Notice that the force due to $q_3$ is much greater than that due to $q_1$. The reason is that even though the charge $q_1$ has a slightly greater magnitude than that of $q_3$, $q_3$ is about 2 times closer to $q_2$ than $q_1$ is.
The surface charge density of the sphere is given as $sigma = + 6.2 :dfrac{mu C}{m^2}$.
So the total charge on the sphere is
$Q = sigma A = +6.2 :dfrac{mu C}{cancel{m^2}} times 0.056 :cancel{m^2} =+0.3472:mu C$.
The magnitude of the electrostatic force between the sphere and a point charge $q=-3.7:mu C$ is given by
$F = k dfrac{|Q| |q|}{r^2}$
where $k = 8.99 times 10^9 : N.m^2.C^{-2}$ and $r$ is the separation between the point charge $q$ and the center of sphere.
This relation can be rewritten for the separation $r$ as
$r = sqrt{dfrac{k |Q| |q|}{F}}$.
The magnitude of the force is given as
$F =2.9 times 10^{-3}:N$.
So, $r = sqrt{dfrac{8.99 times 10^9 times 0.3472 times 10^{-6} times 3.7 times 10^{-6}}{2.9 times 10^{-3}}}$
$$
r = sqrt{dfrac{8.99 times 0.3472 times 3.7}{2.9}} = 2.0:m
$$
$F = dfrac{8.99 times 10^9 times 6.7 times 10^{-6} times Q}{(0.27)^2} = dfrac{8.99 times 6.7 times 10^{3} times Q}{0.0729}$
where $8.99 times 10^9$ is proportionality constant with unit $N.m^2.C^{-2}$.
The magnitude of the force is given as $F = 3.4 times 10^{-3}:N$.
We have
$3.4 times 10^{-3} = dfrac{8.99 times 6.7 times 10^3 times Q}{0.0729}$
So the total charge $Q = dfrac{3.4 times 0.0729 times 10^{-3}}{8.99 times 6.7 times 10^3} = 0.0041 times 10^{-6}:C = 0.0041:mu C$
The surface area of the sphere is $A = 0.042:m^2$.
So the surface charge density of the sphere is
$sigma = dfrac{Q}{A} = dfrac{0.0041: mu C}{0.042 :m^2} =0.098:dfrac{mu C}{m^2}$
This is shown in the figure.
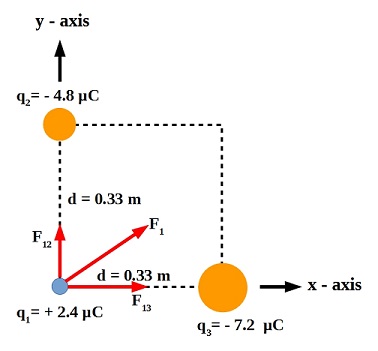
The magnitude of the force $F_{12}$ on $q_1$ due to $q_2$ is given by
$F_{12} = k dfrac{|q_1| |q_2|}{d^2}$
where $k = 8.99 times 10^9 :N.m^2. C^{-2}$.
Substituting the values,
$F_{12} = dfrac{8.99 times 10^9 times 2.4 times 10^{-6} times 4.8 times 10^{-6}}{0.33^2} = 0.95:N$
Both charges are of opposite kind. So the force is attractive and it acts along the $(+)^{ive} :y$-axis as shown in the figure.
So, $vec{F}_{12} = 0.95:hat{y}$
The magnitude of the force $F_{13}$ on $q_1$ due to $q_3$ is given by
$F_{13} = k dfrac{|q_1| |q_3|}{d^2}$
$F_{13} = dfrac{8.99 times 10^9 times 2.4 times 10^{-6} times 7.2 times 10^{-6}}{0.33^2} = 1.43:N$
This is also attractive force and it acts along the $(+)^{ive} :x$-axis.
So, $vec{F}_{13} = 1.43:hat{x}$.
The total force acting on $q_1$ is
$vec{F}_1 = vec{F}_{12} + vec{F}_{13} = 1.43:hat{x} + 0.95:hat{y}$
The magnitude of the total force is
$F_1 = sqrt{(1.43)^2 + (0.95)^2} = 1.72 :N$
$$
{color{#4257b2}text{Picture the Problem}}
$$
The situation is shown in our sketch, with each charge at its appropriate location. Notice that the forces exerted on charge $q_1$ by the charges $q_2$ and $q_3$ are orthogonal (perpendicular to each other). We give the force on $q_1$ due to $q_2$ the label $vec{pmb F}_{12}$ and the force on $q_1$ due to $q_3$ the label $vec{pmb F}_{13}$.
$$
{color{#4257b2}text{Strategy}}
$$
The total force on $q_1$, denoted by $vec{pmb F}_1$, is the vector sum of the forces due to $q_2$ and $q_3$. In particular, notice that the attractive force $vec{pmb F}_{12}$ points upward and the repulsive force $vec{pmb F}_{13}$ points to the left. The magnitude of $vec{pmb F}_{12}$ is $k|q_1||q_2|/d^2 = 2.0kq^2/d^2$, with $q = 2.4;mu$C, $d = 0.33$ m. Similarly, the magnitude of $vec{pmb F}_{13}$ is $k|q_1||q_3|/d^2 = 3.0kq^2/d^2$, with $q = 2.4;mu$C, $d = 0.33$ m.
$$
{color{#4257b2}text{Solution}}
$$
$$
begin{align*}
vec{pmb F}_{12} &= 2.0;kfrac{q^2}{d^2}qquaduparrow\
vec{pmb F}_{13} &= 3.0;kfrac{q^2}{d^2}qquad leftarrow\
vec{pmb F}_1 &= vec{pmb F}_{12} + vec{pmb F}_{13}\
&= 2.0;kfrac{q^2}{d^2};uparrow ;+; 3.0;kfrac{q^2}{d^2};leftarrow\
&= kfrac{q^2}{d^2}left(2.0;uparrow ;+; 3.0;leftarrowright)
end{align*}
$$
Hence, the magnitude of $vec{pmb F}_1$ is
$$
begin{align}
F_1 = kfrac{q^2}{d^2}sqrt{(2.0)^2 + (3.0)^2} = ksqrt{13};frac{q^2}{d^2}
end{align}
$$
Substituting the known values of $q$ and $d$, we find
$$
F_1 = (8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2)timessqrt{13}timesfrac{(2.4times10^{-6};mathrm{C})^2}{(0.33;mathrm{m})^2} = 1.7;mathrm{N}
$$
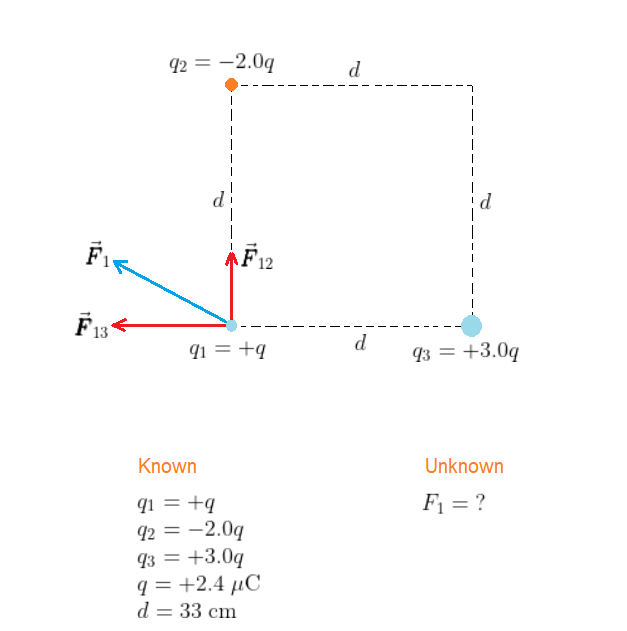
$$
{color{#4257b2}text{Insight}}
$$
We see the result of (a) is the same as in Problem 76. This shouldn’t be a surprise since all what we changed in (a) is the direction of the force $vec{pmb F}_{13}$ exerted on $q_1$ by $q_3$, which doesn’t affect the magnitude of the total force exerted on charge $q_1$.
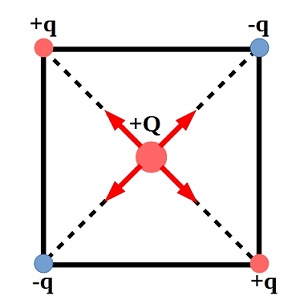
The magnitude of each charge at the corner of the square is $|q|$.
So the magnitude of force on $+Q$ due to each charge at the corner of the square is same. It is given by
$F = k dfrac{|Q||q|}{(d/sqrt{2})^2} = 2kdfrac{|Q||q|}{d^2}$
Both $+q$ charges exert repulsive force on $+Q$. So the direction of the forces are opposite to each other. Since the magnitude is same they cancel each other.
Similarly both $-q$ charges exert attractive force on $+Q$ and they cancel each other.
So the net force on $+Q$ is zero.
The charge configuration and the direction of forces are shown below.
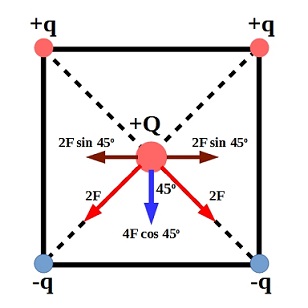
Along one diagonal the $+q$ repels $+Q$ and $-q$ attracts it. So both forces add up and the net force $(2F)$ acts towards $-q$.
Same scenario happens along the other diagonal.
Since both $-q$ charges are at the bottom corner, the vertical components of both forces along each diagonal cancel each other and the horizontal components add up.
It is shown in the following diagram.
So the magnitude of net force is
$F_{net} = 4Fcos(45^o) = 4 times dfrac{^{sqrt{2}}cancel{2}k|Q||q|}{d^2} times dfrac{1}{cancel{sqrt{2}}} = 4sqrt{2} k dfrac{|Q||q|}{d^2}$
The direction of net forces is from the center of the square to the center of the bottom edge as shown in the figure.
{color{#4257b2}text{Picture the Problem}}
$$
The situation is shown in our sketch, with each charge at its appropriate location. Notice that the forces exerted on charge $q_3$ by the charges $q_1$ and $q_2$ are noncolinear (don’t act along the same direction). We give the force on $q_3$ due to $q_1$ the label $vec{pmb F}_{31}$ and the force on $q_3$ due to $q_2$ the label $vec{pmb F}_{32}$.
$$
{color{#4257b2}text{Strategy}}
$$
The total force on $q_3$, denoted by $vec{pmb F}_3$, is the vector sum of the forces due to $q_1$ and $q_2$. In particular, notice that the two forces $vec{pmb F}_{31}$ and $vec{pmb F}_{32}$ are attractive and directed in such a way the angle between them is $60^circ$ (from the properties of the equilateral triangle). The magnitude of $vec{pmb F}_{31}$ is $k|q_1||q_3|/d^2$, with $d = 0.0435$ m. Similarly, the magnitude of $vec{pmb F}_{32}$ is $k|q_2||q_3|/d^2$, with $d = 0.0435$ m.
$$
{color{#4257b2}text{Solution}}
$$
$$
begin{align*}
vec{pmb F}_{31} &= kfrac{|q_1||q_3|}{d^2}\
&= (8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2)timesfrac{(2.1times10^{-6};mathrm{C})(0.89times10^{-6};mathrm{C})}{(0.0435;mathrm{m})^2}\
&= 8.9;mathrm{N}qquadleftarrow\
vec{pmb F}_{32} &= kfrac{|q_2||q_3|}{r^2}\
&= (8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2)timesfrac{(6.3times10^{-6};mathrm{C})(0.89times10^{-6};mathrm{C})}{(0.0435;mathrm{m})^2}\
&= 27;mathrm{N}qquadnwarrow
end{align*}
$$
From the geometry of the force parallelogram, we find the magnitude of $vec{pmb F}_3$ is
$$
begin{align*}
F_3 &= sqrt{F_{31}^2 + F_{32}^2 + 2F_{31}F_{32}cos60^circ}\
&= sqrt{(8.9;mathrm{N})^2 + (27;mathrm{N})^2 + 2(8.9;mathrm{N})(27;mathrm{N})cos60^circ}\
&= 32;mathrm{N}
end{align*}
$$
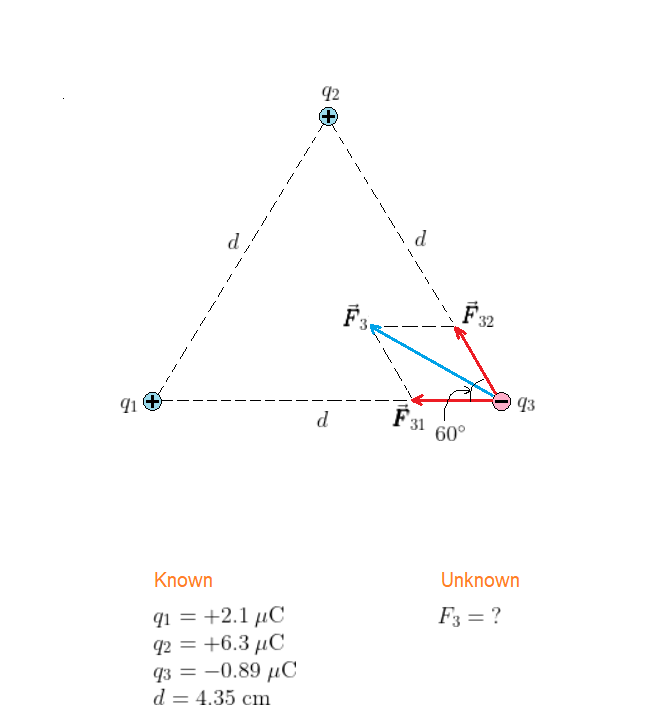
{color{#4257b2}text{Insight}}
$$
If the two forces acting on $q_3$ due to $q_1$ and $q_2$ were collinear, we would have a maximum answer of (8.9 N + 27 N) = 36 N. If the forces were orthogonal, the answer would be 28 N. In such case, we expect our answer to be something in between, which is so; our result gives 32 N.
The situation is shown in our sketch. Notice that when the center-to-center distance of the spheres is 33 cm, the repulsive force experienced by the spheres is 0.75 N. We give one sphere and its radius the labels S$_1$ and $r_1$, respectively. Similarly, we give the other sphere and its radius the labels S$_2$ and $r_2$, respectively. We also suppose the total charge on S$_1$ is $Q_1$ and the total charge on S$_2$ is $Q_2$.
$text{color{#4257b2}Strategy}$
To each sphere the other sphere behaves as a point charge at its center with its total charge concentrated there. In such sense, we are allowed to apply Coulomb’s law to the two charged spheres, from which we obtain an equation in the unknown quantities $|Q_1|$ and $|Q_2|$. The second equation follows from the fact that the combined charge of the two spheres is a given, known value. Solving the two equations simultaneously gives us the magnitude of charge on each sphere and thus the surface charge density on each one.
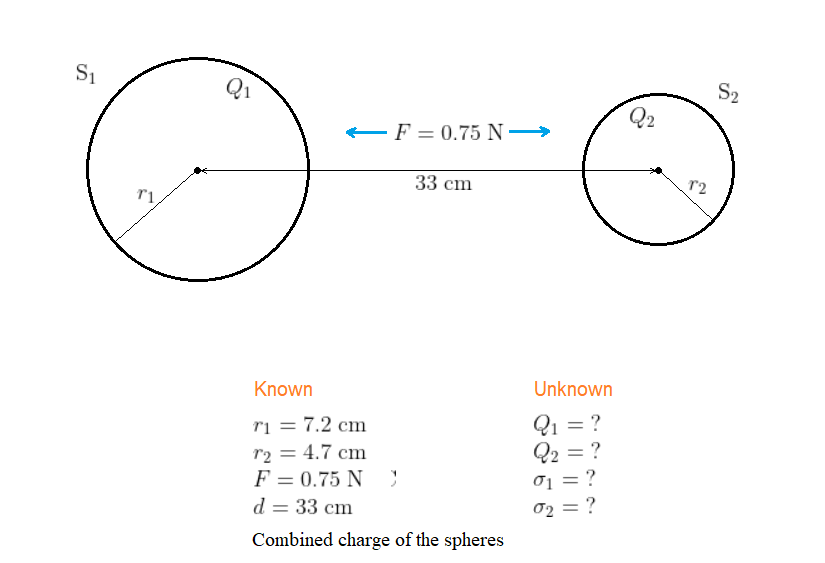
Applying Coulomb’s law to the spheres, with magnitudes of charge $|Q_1|$ and $|Q_2$, we obtain
$$
F = kfrac{|Q_1||Q_2|}{d^2}
$$
which leads to
$$
|Q_1||Q_2| = frac{Fd^2}{k} = frac{(0.75;mathrm{N})(0.33;mathrm{m})^2}{8.99times10^{9};mathrm{N}cdotmathrm{m}^2/mathrm{C}^2} = 9.1;mu^2mathrm{C}^2
$$
At the same time, we know that $|Q1| + |Q_2| = 55;mu$C. Solving for $|Q_2|$ and substituting the result into the former equation, we have
$$
|Q_1|(55;mumathrm{C} – |Q_1|) = 9.1;mu^2mathrm{C}^2
$$
Rearranging the equation yields the following quadratic equation in $|Q_1|$:
$$
|Q_1|^2 – (55;mumathrm{C})|Q_1| + 9.1;mu^2mathrm{C}^2 = 0
$$
which gives us two distinct solutions. We consider each solution at a time.
$textbf{The first solution}$
We have $|Q_1| = 54.8;mu$C, which leads to $|Q_2| = 0.20;mu$C. Since the electric force between the two spheres is repulsive and their total charge is positive in sign, we conclude the individual charge on each sphere is also positive in sign. In such case, the surface charge density on S$_1$ is
$$
sigma_1 = +frac{|Q_1|}{4pi r^2} = frac{54.8times10^{-6};mathrm{C}}{4pi(0.072;mathrm{m})^2} = 0.84;mathrm{mC/m^2}
$$
and the surface charge density on S$_2$ is
$$
sigma_2 = +frac{|Q_2|}{4pi r^2} = frac{0.20times10^{-6};mathrm{C}}{4pi(0.047;mathrm{m})^2} = 7.2;mumathrm{C/m^2}
$$
$textbf{The second solution}$
We have $|Q_1| = 0.17;mu$C, which leads to $|Q_2| = 55;mu$C. In such case, the surface charge density on S$_1$ is
$$
sigma_1 = +frac{|Q_1|}{4pi r^2} = frac{0.17times10^{-6};mathrm{C}}{4pi(0.072;mathrm{m})^2} = 2.6;mumathrm{C/m^2}
$$
and the surface charge density on S$_2$ is
$$
sigma_2 = +frac{|Q_2|}{4pi r^2} = frac{55 times10^{-6};mathrm{C}}{4pi(0.047;mathrm{m})^2} = 2.0;mathrm{mC/m^2}
$$
Due to the symmetry of the problem (the symmetry of Coulomb’s law), we can only determine the charges of the two spheres, without specifying which charge corresponds to which sphere (this result is independent of the size of each sphere); you can see this very clear in the mathematical expression for Coulomb’s law, as you obtain the same result upon interchanging the two quantities $|Q_1|$ and $|Q_2|$. This symmetry breaks once we are to evaluate the surface charge density on each charge, as this brings the size’s asymmetry of the spheres into the picture, which explains why we eventually end up with two sets of solution.
This problem is a direct application to Coulomb’s law for electrostatic forces between electric charges. First, we use the given value for the magnitude of the electric force in system D to find the value of the magnitude of the charge $|q|$. Then, we use this value to find the electric force in the subsequent systems.
$text{color{#4257b2}Solution}$
Applying Coulomb’s law to system D, we obtain
$$
F = kfrac{|q||q|}{r^2} = kfrac{|q|^2}{r^2}
$$
which leads to
$$
|q| = rsqrt{frac{F}{k}} = (1;mathrm{m})sqrt{frac{1;mathrm{N}}{8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2}} = 10.5;mumathrm{C}
$$
$textbf{(a)}$ Applying Coulomb’s law to system A, we obtain
$$
F = kfrac{|2q||-4q|}{r^2} = kfrac{8|q|^2}{r^2}
$$
Substituting the known values of $|q|$ and $r$, we find
$$
F = (8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2)timesfrac{8left(10.5times10^{-6};mathrm{C}right)^2}{(1;mathrm{m})^2} = 7.93;mathrm{N}
$$
$textbf{(b)}$ Applying Coulomb’s law to system B, we obtain
$$
F = kfrac{|-16q||4q|}{r^2} = kfrac{64|q|^2}{r^2}
$$
Substituting the known values of $|q|$ and $r$, we find
$$
F = (8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2)timesfrac{64left(10.5times10^{-6};mathrm{C}right)^2}{(4;mathrm{m})^2} = 3.96;mathrm{N}
$$
$textbf{(c)}$ Applying Coulomb’s law to system C, we obtain
$$
F = kfrac{|6q||-6q|}{r^2} = kfrac{36|q|^2}{r^2}
$$
Substituting the known values of $|q|$ and $r$, we find
$$
F = (8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2)timesfrac{36left(10.5times10^{-6};mathrm{C}right)^2}{(6;mathrm{m})^2} = 0.991;mathrm{N}
$$
For the charges outside the spherical shell, the spherical shell (with a uniform charge distribution) behaves as if all its charge $+Q$ were concentrated in a point at it center; in such case, we can apply Coulomb’s law to calculate the magnitude of the force exerted on each charge by the sphere. The charges inside the hollow sphere experience zero force.
$text{color{#4257b2}Solution}$
Consider the charge $q_1$. This charge is inside the hollow sphere. Thus the force exerted on $q_1$ by the sphere is identically zero ($F_1 = 0$).
Consider the charge $q_2$. This charge is outside the spherical shell. Accordingly, the magnitude of the force exerted on $q_2$ by the sphere is given by Coulomb’s law:
$$
F_2 = kfrac{|q_2||Q|}{(3d)^2} = kfrac{|+2q||Q|}{9d^2} = frac{2}{9}F
$$
where we define $Fequiv k|q||Q|/d^2$
Consider the charge $q_3$, which is located outside the spherical shell. The magnitude of the force exerted on $q_3$ by the sphere is given by Coulomb’s law:
$$
F_3 = kfrac{|q_3||Q|}{(2d)^2} = kfrac{|-3q||Q|}{4d^2} = frac{3}{4}F
$$
Consider the charge $q_4$, which is located outside the spherical shell. The magnitude of the force exerted on $q_4$ by the sphere is given by Coulomb’s law:
$$
F_4 = kfrac{|q_4||Q|}{(3d)^2} = kfrac{|-4q||Q|}{9d^2} = frac{4}{9}F
$$
Consider the charge $q_5$, which is located outside the spherical shell. The magnitude of the force exerted on $q_5$ by the sphere is given by Coulomb’s law:
$$
F_5 = kfrac{|q_5||Q|}{(2d)^2} = kfrac{|-5q||Q|}{4d^2} = frac{5}{4}F
$$
We see $F_1 < F_2 < F_4 < F_3 < F_5$. Therefore, the rank of the point charges in order of increasing magnitude of the force exerted on them by the sphere is $q_1 < q_2 < q_4 < q_3 < q_5$.
q_1 < q_2 < q_4 < q_3 < q_5
$$
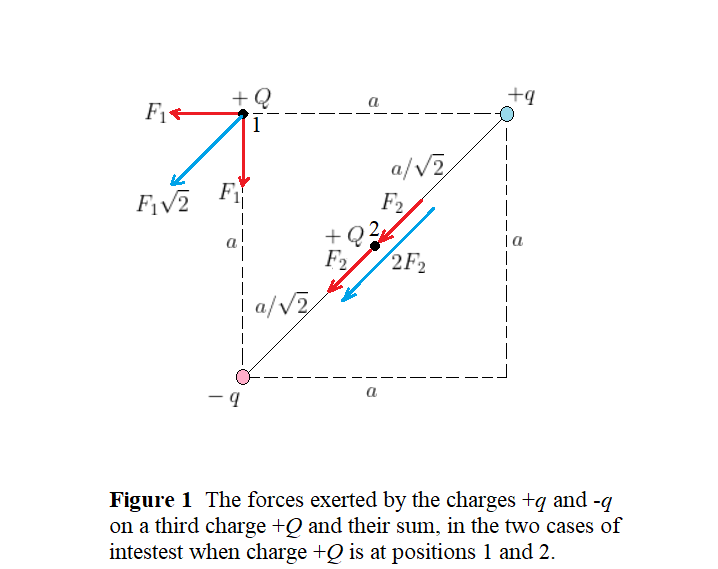
The situation is shown in Fig. 1, with the two charges $+q$ and $-q$ at their appropriate places and the third charge $+Q$ placed once at position 1 (at one empty corner of the square) and once at position 2 (at the center of the square). Notice that the forces experienced by the charge $+Q$ due to the charges $+q$ and $-q$ are orthogonal in case 1 and colinear in case 2.
$text{color{#4257b2}Strategy}$
We first note that because the charges $+q$ and $-q$ have the same magnitude of charge $|q|$ and in the two cases 1 & 2 they are the same distance from the location of the third charge ($+Q$), the magnitude of the forces exerted by them on $+Q$ are equal; we call them $F_1$ in case 1 and $F_2$ in case 2. Next, it may seem obvious that the magnitude of the total force exerted by the charges $+q$ and $-q$ on charge $+Q$ is greater in case 2, as the individual force vectors are aligned in the same direction, in addition that the distance from these charges to the third charge $+Q$ is less in case 2 than that in case 1 (from the geometric properties of the square). Thus we expect a third point charge experiences a greater total force in case 2 (if the charge is placed at the center of the square); the following calculations will confirm this result.
$text{color{#4257b2}Solution}$
In case 1, the charge $+Q$ is distance $a$ from the both charges $+q$ and $-q$. Thus the force magnitude $F_1$ is
$$
F_1 = kfrac{|q||Q|}{a^2}
$$
and so the total force experienced by the charge $+Q$ is $F_1sqrt{2}$ (the individual forces are orthogonal).
In case 2, the charge $+Q$ is distance $a/sqrt{2}$ from the both charges $+q$ and $-q$. Thus the force magnitude $F_2$ is
$$
F_2 = kfrac{|q||Q|}{(a/sqrt{2})^2} = 2kfrac{|q||Q|}{a^2} = 2F_1
$$
and so the total force experienced by the charge $+Q$ is $4F_1$ (the individual forces are colinear).
Clearly, we have $4F_1;(text{case 2}) > F_1sqrt{2};(text{case 1})$, and we see, indeed, the total force experienced by a third charge is greater in case 2, in which the charge is placed at the center of the square.
Total charge transferred in $4.5:s$ is $4.5 times 0.3 = 1.35:C$.
The magnitude of charge of an electron is $|e| = 1.6 times 10^{-19}:C$.
So the number of electrons in $1.35:C$ charge is
$dfrac{1.35}{1.6 times 10^{-19}} = 84375 times 10^{14}$ electrons.
The total charge of the system is positive, so we conclude the system contains more number of protons than electrons. But the precise numbers of the two particles require mathematical calculations. First, we suppose the system contains $n$ number of electrons and $p$ number of protons. This allows us to express the total charge of the system in terms of $n$ and $p$ and equate it with the given value of $1.84times10^{-15}$ C, which gives us the first equation in the unknown quantities $n$ and $p$. The second equation follows from the fact that the total mass of the system, which is also to be expressed in terms of $n$ and $p$, is a given, known value. Solving the two equations simultaneously gives us the required values of $n$ and $p$.
$text{color{#4257b2}Solution}$
Electrons have a negative charge $-e$ and protons have a positive charge $e$. Thus the total charge of the system is given as
$$
n(-e) + p(e) = 1.84times10^{-15};mathrm{C}
$$
which simplifies to
$$
begin{align*}
-n + p &= frac{1.84times10^{-15};mathrm{C}}{1.60times10^{-19};mathrm{C}}\
-n + p &= 11,500 && (1)
end{align*}
$$
The mass of the electron is $m_e = 9.11times10^{-31}$ kg and the mass of the proton is $m_p =1.67times10^{-27}$ kg. We can express the total mass of the system and simplify the result as follows
$$
begin{align*}
m_en + m_pp &= 4.56times10^{-23};mathrm{kg}\
(9.11times10^{-31};mathrm{kg})n + (1.67times10^{-27};mathrm{kg})m &= 4.56times10^{-23};mathrm{kg}\
n + 1,830p & = 5.01times10^7 && (2)
end{align*}
$$
$$
begin{align*}
n + 1,830(n + 11,500) & = 5.01times10^7\
(1 + 1,830)n &= 5.01times10^7 – 2.10times10^7\
n &= frac{(5.01 – 2.10)times10^7}{1 + 1,830}\
&= 15,900;;mathrm{electrons}
end{align*}
$$
$textbf{(b)}$ Substituting the result for $n$ back into Equation (1) and solving for $p$, we find
$$
p = 15,900 + 11,500 = 27,400;;mathrm{protons}
$$
The total (net) force exerted on each charge is the vector sum of the individual forces exerted on this charge due to the other charges. From the elementary vector analysis, the smaller is the angle subtended by two given vectors, the larger is the length of their vector sum (the maximum sum is obtained with the two vectors aligned in the same direction). Accordingly, the charge $q_1$ experiences the total force with the greatest magnitude, then come the charges $q_2$ and $q_3$, which by symmetry both experience a total force of the same magnitude but less than that of $q_1$.
Indeed, from the geometry of the equilateral triangle in our sketch, we see the net force exerted on $q_1$ is equal to $2Fcos30^circ = Fsqrt{3}$, and the net force exerted on $q_2$ or $q_3$ is equal to $2Fcos60^circ = F$. Hence, the rank of the three charges in order of increasing magnitude of the total electric force they experience is given as $q_2 = q_3 < q_1$.
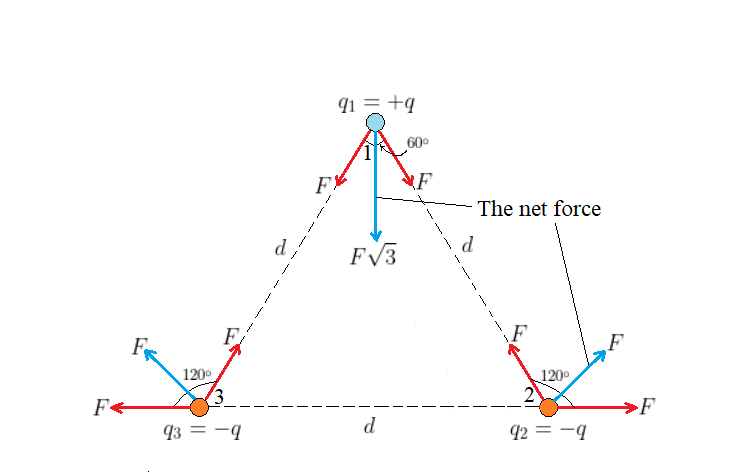
q_2 = q_3 < q_1
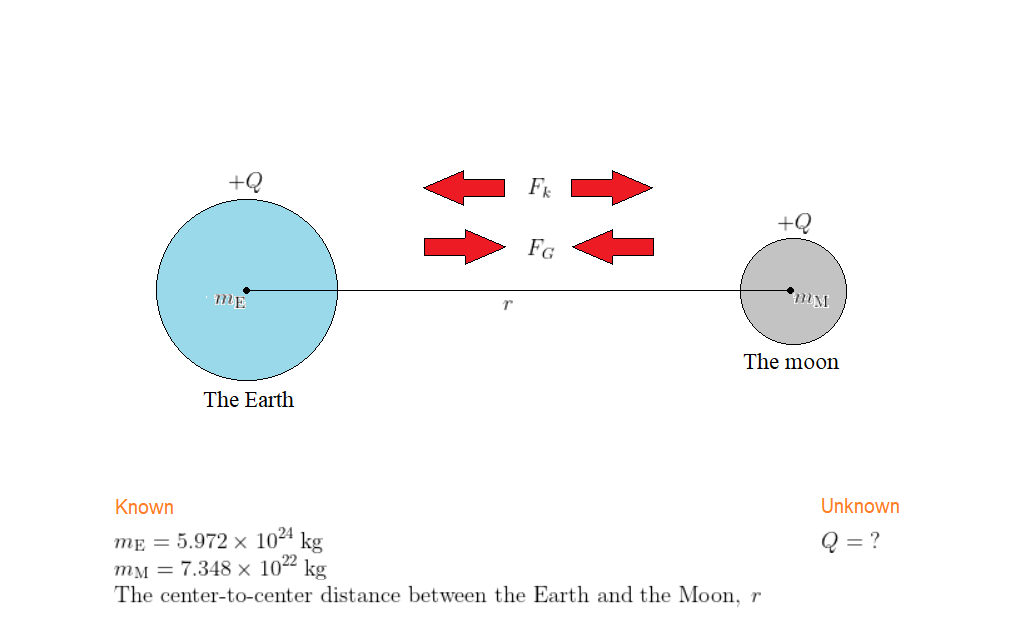
$$
The situation is shown in our sketch, along with the known values of the Earth’s mass $m_{rm E}$ and the Moon’s mass $m_{rm M}$. Note that mutual gravitational force, with magnitude say $F_G$, of the Earth and the Moon acts inward along line connecting their centers. Since the Earth and the Moon carry a charge $+Q$ each, there arises an electrically repulsive force, with magnitude say $F_k$, which acts outward and in the opposite direction of the gravitational force. We also call the center-to-center separation of the Earth and the Moon is $r$. The main strategy is to express the force magnitude $F_G$ using Newton’s law of gravitational forces and the force magnitude $F_k$ using Coulomb’s law of electrostatic forces, then we equate the two results and solve for the required value of $Q$.
$text{color{#4257b2}Solution}$
Applying Newton’s law of gravitation, we have
$$
F_G = Gfrac{m_{rm E}m_{rm M}}{r^2}
$$
Applying Coulomb’s law, we obtain
$$
F_k = kfrac{Q^2}{r^2}
$$
The balance condition requires that $F_G = F_k$. Substituting the above results gives
$$
Gfrac{m_{rm E}m_{rm M}}{r^2} = kfrac{Q^2}{r^2}
$$
Solving for $Q$ and substituting the known values, we find
$$
begin{align*}
Q &= sqrt{frac{Gm_{rm E}m_{rm M}}{k}}\
&= displaystylesqrt{frac{(6.674times10^{-11};mathrm{N}cdotmathrm{m^2}/mathrm{kg}^2)(5.972times10^{24};mathrm{kg})(7.348times10^{22};mathrm{kg})}{8.988times10^9;mathrm{N}cdotmathrm{m^2}/mathrm{C}^2}}\
&= 5.708times10^{13};mathrm{C}
end{align*}
$$
$text{color{#4257b2}Insight}$
Notice that the final result doesn’t depend on the separation $r$ between the Earth and the Moon. Also, the reason the final result for $Q$ is quite small (compared to the massive masses of the Earth and the moon), is the huge relative difference in magnitude between the gravitational constant $G$ (which is a very small number) and the Coulomb’s constant $k$ (which is a very large number) in the SI units.
$Arightarrow -Q$,
$Brightarrow +Q$,
$$
Crightarrow 0
$$
The situation is shown in our sketch, with each charge at its appropriate location. Notice that the forces exerted on charge 1 by charges 2 and 3 are noncolinear (not in the same direction). Because the charges 2 & 3 have the same magnitude of charge $|q|$ and also are the same distance $d$ from charge 1, the forces charge 1 experiences due to charges 2 & 3 have the same magnitude, which we give it the label $F$. The total force acting on charge 1 is the vector sum of the two noncolinear forces with magnitude $F$.
$text{color{#4257b2}Solution}$
The magnitude of the forces exerted on charge 1 by charges 2 & 3 is
$$
F = kfrac{|q|^2}{d^2}
$$
Referring to the geometry of the sketch, the magnitude of net force acting on charge 1 is
$$
F_1 = 2Fcos30^circ = 2kfrac{|q|^2}{d^2}timesfrac{sqrt{3}}{2} = ksqrt{3};frac{|q|^2}{d^2}
$$
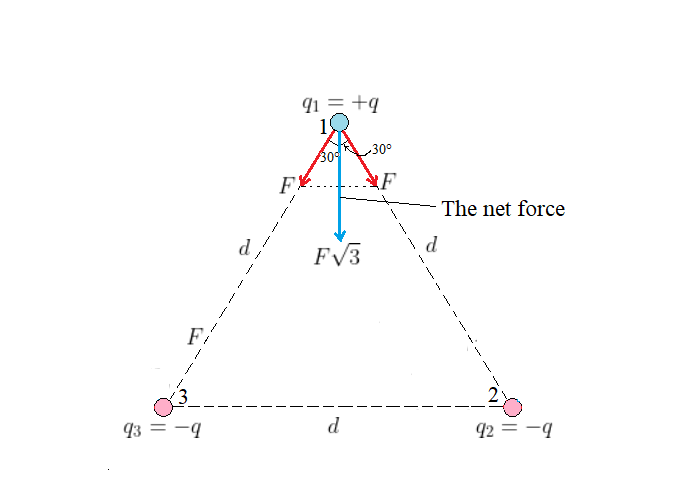
ksqrt{3};dfrac{|q|^2}{d^2}
$$
The situation is shown in our sketch, with each charge at its appropriate location. We will consider charge 1 only, as by symmetry the same results apply equally to charge 3. We first note that the force exerted on charge 1 due to charge 2, with magnitude designated as $F_{qq}$, is repulsive and thus directed along the diagonal of the square and away from it. This leaves us no choice but to assume the sign of the charge $Q$ is $negative$, so that the attractive forces acting on the (positive) charge 1 by charges 2 and 4 (of charge $Q$) counteract the repulsive force of $F_{qq}$; These attractive forces have the same magnitude, denoted by $F_{qQ}$ each, as charges 2 and 4 have the same magnitude of charge and are the same distance $L$ from charge 1. We notice the attractive forces (of $F_{qQ}$) are orthogonal and they have a vector sum, whose magnitude is $F_Q$, that balances the force $F_{qq}$, that is directed along the diagonal of the square and in the opposite direction of the force $F_{qq}$, which is what we need.
The key idea to find the magnitude of the charge $Q$ is that we choose just the right value of $|Q|$ that leads to the balance condition, $F_{qq} = F_Q$ (so that charge 1 experiences zero total force). To do so, we use Coulomb’s law and the vector addition to obtain expressions for $F_{qq}$ and $F_Q$, then we equate the two expressions and solve for $|Q|$.
$text{color{#4257b2}Solution}$
Using Coulomb’s law, the magnitude of the repulsive force exerted by charge 3 on charge 1 is
$$
begin{align}
F_{qq} = kfrac{|q|^2}{left(Lsqrt{2}right)^2} = kfrac{|q|^2}{2L^2}
end{align}
$$
and the magnitude of the individual forces exerted by charges 2 & 4 on charge 1 is
$$
F_{qQ} = kfrac{|q||Q|}{L^2}
$$
Referring to the geometry of the sketch, the sum of the attractive forces of magnitude $F_{qQ}$ has the magnitude
$$
begin{align*}
F_Q &= 2F_{qQ}cos45^circ\
F_Q &= 2kfrac{|q||Q|}{L^2}timesfrac{sqrt{2}}{2}\
F_Q &= ksqrt{2};frac{|q||Q|}{L^2} && (2)
end{align*}
$$
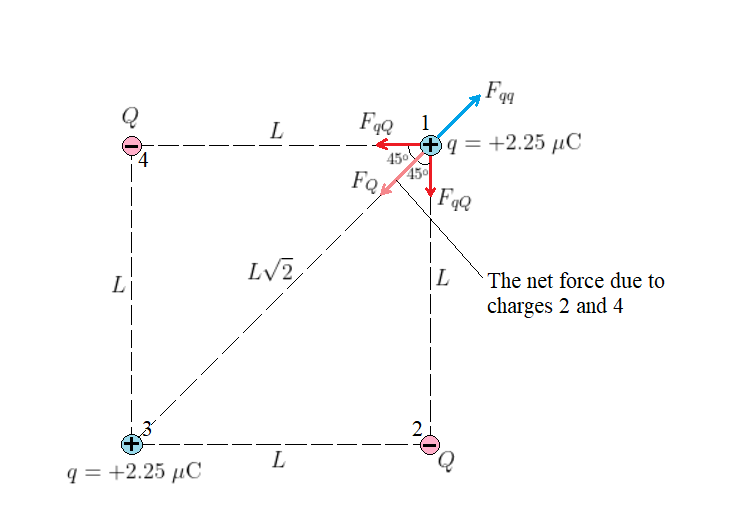
$$
kfrac{|q|^2}{2L^2} = ksqrt{2};frac{|q||Q|}{L^2}
$$
Solving for $|Q|$ and substituting the known values of $|q|$, we find
$$
|Q| = frac{|q|}{2sqrt{2}} = frac{2.25;mumathrm{C}}{2sqrt{2}} = 0.795;mumathrm{C}
$$
Hence, we say the charge $Q = -0.795;mu$C is required at the corners 2 and 4 of the square in order for charge 1 to experience zero total force. By symmetry this result also holds true for charge 3.
$text{color{#4257b2}Insight}$
Notice that the final result for $|Q|$ is independent of the dimension of the square, $L$.
Figure 1b shows the situation when the charge $q$ on the positive $x$ axis is moved to the center of the circle. Now, the charge $q$ on the negative $x$ axis has no balancing charge on the positive side of the horizontal diagonal, and thus all the individual forces acting on charge $q$ at the center of the circle cancel out in pairs, leaving the unbalanced force due to the charge $q$ at $x = -R$ alone. The net force on charge $q$ at the center of the circle is, therefore, equal to this unbalanced force.
$textbf{(a)}$ Since the total force on charge $q$ at the center of the circle is due to the single, unbalanced force exerted by the charge on the negative $x$ axis, the net force is repulsive and directed toward the right (in the positive $x$ direction).
$textbf{(b)}$ The magnitude of the total force exerted on charge $q$ at the center of the circle is the same as the magnitude of the unbalanced force due to the charge $q$ at $x = – R$, which is equal to
$$
kfrac{|q|^2}{R^2}
$$
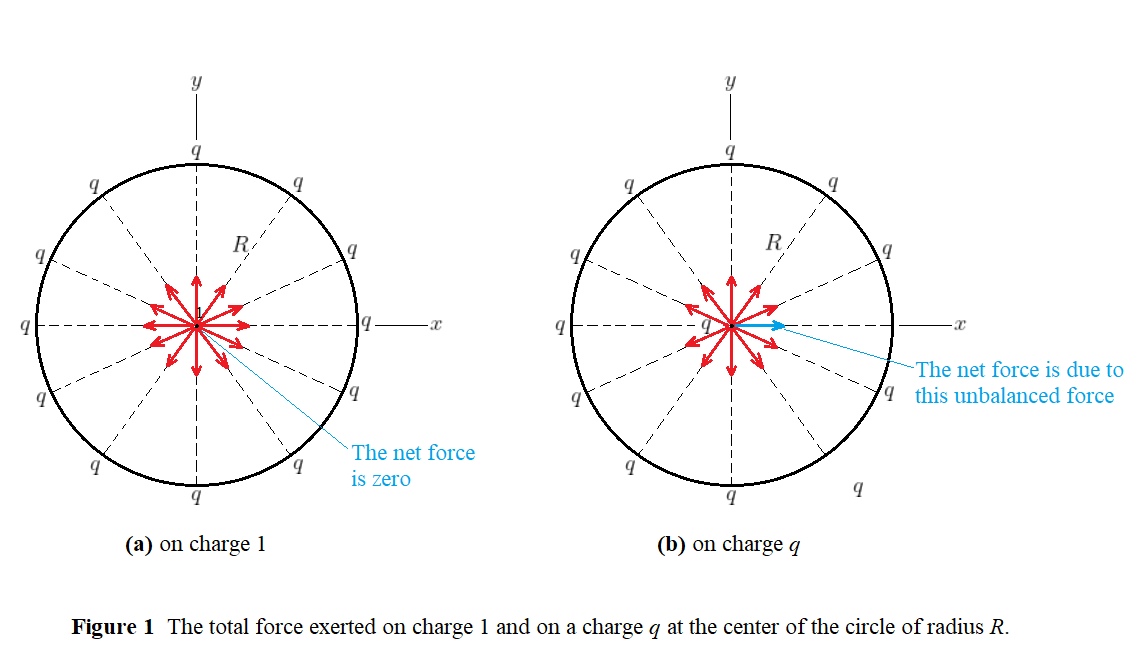
Figure 1 shows the charge configuration of our problem. Note that we take advantage of the symmetry of the problem and place the fifth charge, $q$, at the center of the square. In such case, it suffices to consider only charge 1 and by symmetry the same results are applied equally to the other identical charges, $+Q$.
Note that the repulsive forces exerted on charge 1 due to charges 2 and 4 have the same magnitude (that is $F_2 = F_4$), as charges 2 and 4 are identical and at the same distance from charge 1. These forces are orthogonal such that their vector sum is the net force, with magnitude $F_{2+4}$, which points along the diagonal of the square and away of its center. Since the force on charge 1 due to charge 3 is also repulsive and directed along the diagonal of the square, away from its center, we are given no choice but to assume the fifth charge, $q$, at the center of the square has a $negative$ sign, as the attractive force exerted by this charge on charge 1 (whose magnitude is given the label $F_q$) will point along the diagonal of the square and toward its center, such that it balances the other repulsive forces.
Finally, to determine the magnitude of the fifth charge $|q|$, what we need to do is to balance the force $F_q$, which points toward the center of the square, with the combined forces of $F_{2+4}$ and $F_3$, which point away from the center of the square, and use Coulomb’s law to solve for the corresponding value of $|q|$.
$text{color{#4257b2}Solution}$
From Coulomb’s law the magnitude of the forces acting on charge 1 by charges 2 and 4 is
$$
F_2 = F_4 = kfrac{|Q|^2}{d^2}
$$
From the geometry of Fig. 1 the net force on charge 1 due to charges 2 and 4 is therefore
$$
begin{align}
F_{2+4} = F_2sqrt{2}
end{align}
$$
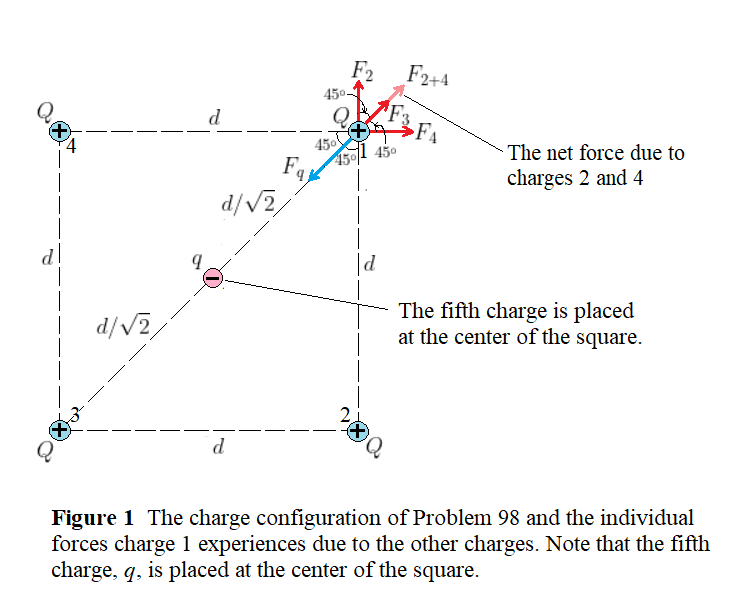
$$
begin{align*}
F_3 = kfrac{|Q|^2}{left(dsqrt{2}right)^2} = frac{F_2}{2} && (2)
end{align*}
$$
and the magnitude of the force on charge 1 due to the charge $q$ is
$$
begin{align*}
F_q = kfrac{|q||Q|}{left(d/sqrt{2}right)^2} = frac{2|q|}{|Q|}F_2 && (3)
end{align*}
$$
where we used $F_2 = k|Q|^2/d^2$.
The balance condition tells us $F_q = F_{2+4} + F_3$, or substituting the expressions of the forces from Equations (1), (2) and (3), we obtain
$$
frac{2|q|}{|Q|}F_2 = F_2sqrt{2} + frac{F_2}{2}
$$
Simplifying the result and solving for $|q|$, we find
$$
|q| = left(frac{sqrt{2}}{2} + frac{1}{4}right)|Q| = 0.957|Q|
$$
To summarize the results, we say we need to place the charge $q = -0.957Q$ at the center of square such that the total electric force acting on charge 1, and by symmetry on each of the charges 2, 3 and 4, is zero.
$text{color{#4257b2}Insight}$
The final result for $|q|$ is independent of the dimension of the square, $d$.
-0.957Q
$$
The total force on charge 3 is the vector sum of the forces due to charges 1 and 2. Because charges 1 and 2 have the same magnitude and are the same distance, $d$, from charge 3, the forces $vec{pmb F}_{31}$ and $vec{pmb F}_{32}$ have the same magnitude, which is equal to
$$
F_{31} = F_{32} = kfrac{|q_1||q_3|}{d^2}
$$
Referring to the geometry of Fig. 1, we see, by symmetry, the net force $vec{pmb F}_3$ acts downward, with the following magnitude
$$
F_3 = 2F_{31}cos60^circ = 2kfrac{|q_1||q_3|}{d^2}timesfrac{1}{2} = kfrac{|q_1||q_3|}{d^2}
$$
Substituting the known values, we find
$$
F_3 = (8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2)timesfrac{(7.3times10^{-6};mathrm{C})^2}{(0.63;mathrm{m})^2} = 1.2;mathrm{N}
$$
We see the net force has a magnitude of 1.2 N, and it points downward (in the negative $y$ direction).
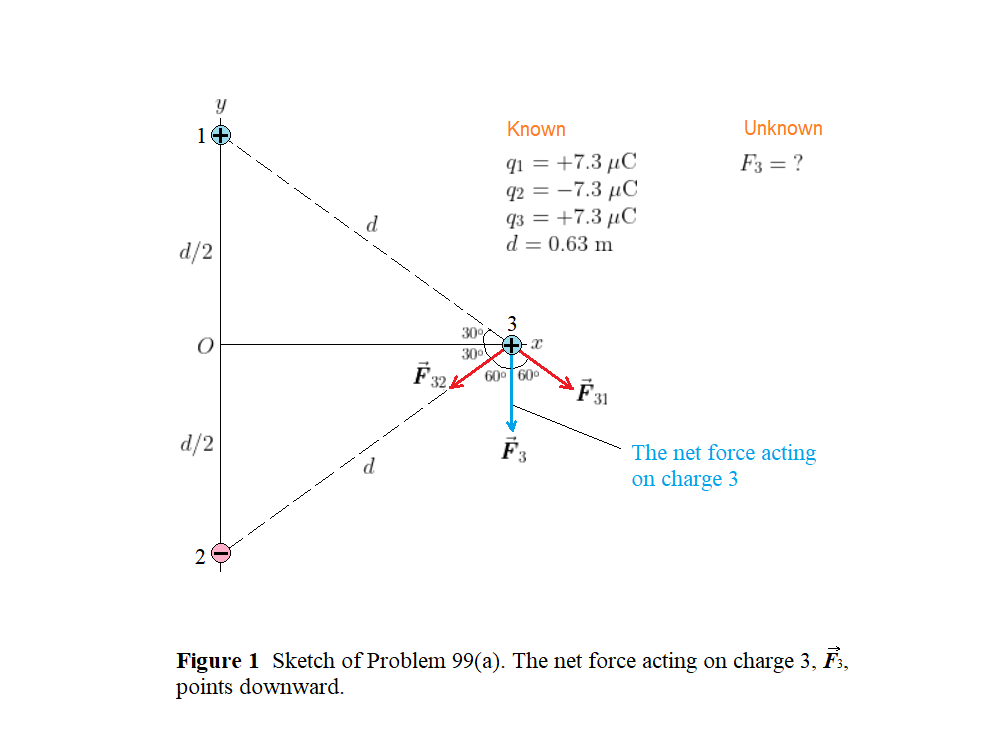
$textbf{(c)}$ Referring to Fig. 2, we notice the total force on charge 3 points downward and has the following magnitude
$$
F_3 = F_{31} + F_{32}
$$
But the forces due to charges 1 and 2 have the same magnitude of $k|q_1||q_2|/(d/2)^2$. Hence,
$$
F_3 = 2kfrac{|q_1||q_2|}{(d/2)^2} = 8kfrac{|q_1||q_2|}{d^2}
$$
which is 8 times greater than that in part (a). The answer is therefore equal to $8times(1.2;mathrm{N}) = 9.6$ N. We see the total force acting on charge 3 when it is at the origin has a magnitude of 9.6 N, and it points downward (in the negative $y$ direction).
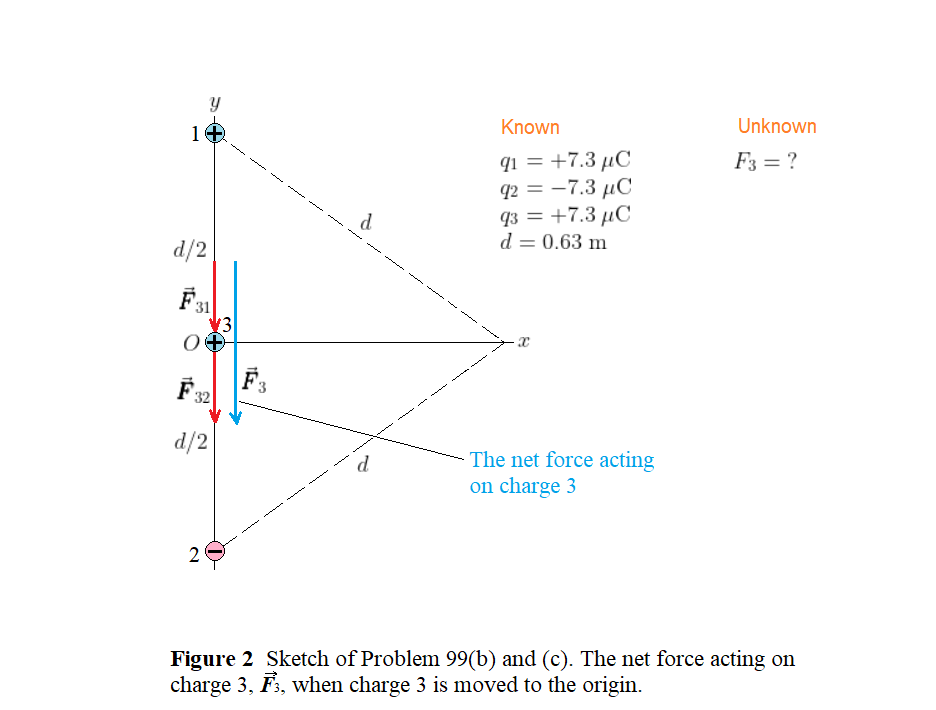
$textbf{(b)}$ greater
$textbf{(c)}$ 9.6 N (in the negative $y$ direction)
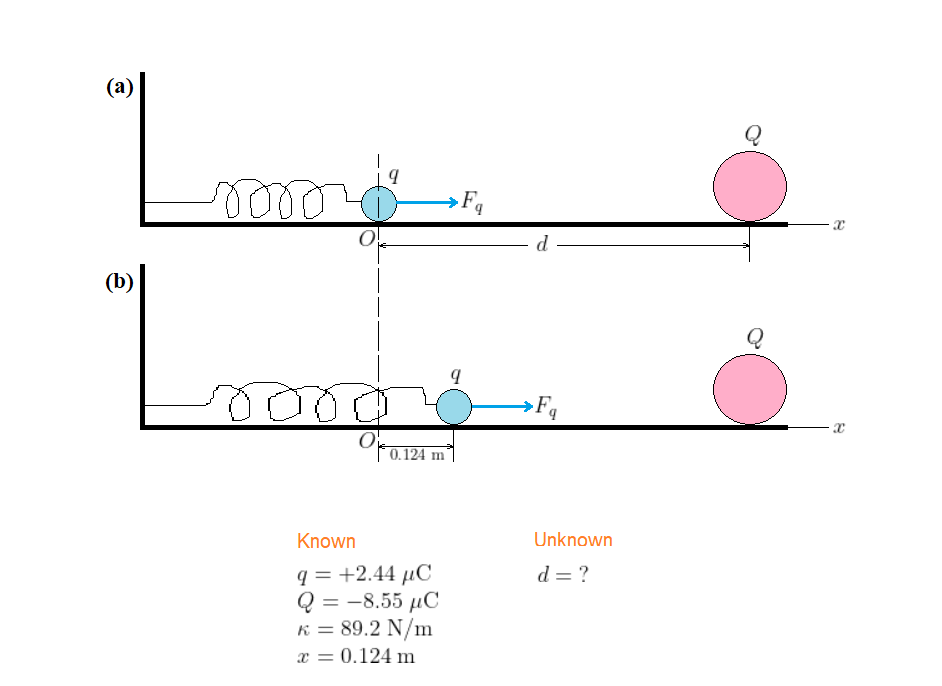
The situation is shown in our sketch, once when the small charge is at rest at the origin (see case (a)) and another when the spring is stretched and the small charge is at $x = 0.124$ m (see case (b)).
As shown in case (a), when the charge $Q$ is brought close to the small charge $q$, at a distance $d$ from it, an electric force, with a certain magnitude we call $F_q$, is exerted on the charge $q$ due to the charge $Q$. This force is attractive and directed toward the right (in the positive $x$ axis), which then causes the spring to stretch and the charge $q$ to move to the position $x = 0.124$ m (see case (b)). In such case, the magnitude $F_q$ of the electric force is related to the displacement $x = 0.124$ m by Hook’s law for a spring.
The key idea is to express $F_q$ in two ways; once (in terms of the unknow variable $d$) using Coulomb’s law and another time (in terms of the known value $x$) using Hook’s law. The two expressions are equal, from which we can solve for $d$.
$text{color{#4257b2}Solution}$
From Coulomb’s law the magnitude of the electric force is
$$
F_q = kfrac{|q||Q|}{d^2}
$$
From Hooke’s law the magnitude of the spring force is given by $kappa x$, with $x = 0.124$ m. Hence, we can write
$$
kfrac{|q||Q|}{d^2} = kappa x
$$
Solving for $d$ gives
$$
d = sqrt{frac{k|q||Q|}{kappa x}}
$$
Substituting the known values, we find
$$
begin{align*}
d &= sqrt{frac{(8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2)(2.44times10^{-6};mathrm{C})(8.55times10^{-6};mathrm{C})}{(89.2;mathrm{N/m})(0.124;mathrm{m})}}\
&= 0.130;mathrm{m}
end{align*}
$$
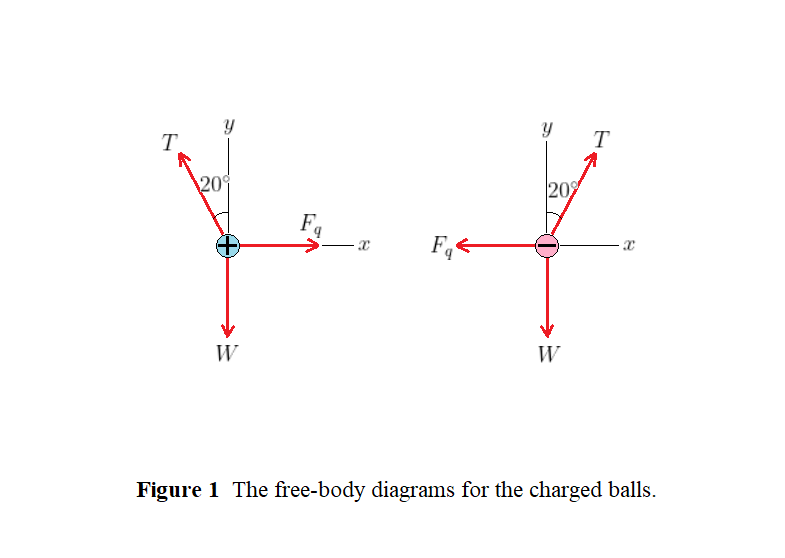
Consider the force components along the $y$ direction. The $y$ component of the tension force is $T_y = Tcos20^circ$. The $y$ component of the weight is $W_y = – mtextit{g}$. We set the net force in the $y$ direction equal to zero, $displaystyleSigma F_y = 0$:
$$
begin{align}
Tcos20^circ – mtextit{g} = 0
end{align}
$$
Consider the force components along the $x$ direction. The $x$ component of the tension force is $T_x = Tsin20^circ$. The horizontal force $F_q$ acts in the negative $x$ direction. We set the net force in the $x$ direction equal to zero, $displaystyleSigma F_x = 0$:
$$
begin{align}
Tsin20^circ – F_q = 0
end{align}
$$
$textbf{(a)}$ Eliminating $T$ from Equations (1) and (2) gives
$$
F_q = mtextit{g}tan20^circ
$$
Substituting the known values, we find
$$
F_q = (0.14times10^{-3};mathrm{kg})(9.8;mathrm{m/s}^2)tan20^circ = 5.0times10^{-4};mathrm{N}
$$
$$
T = frac{F_q}{sin20^circ}
$$
Substituting the known value of $F_q$ (from (a)), we find
$$
T = frac{5.0times10^{-4};mathrm{N}}{sin20^circ} = 1.5times0^{-3};mathrm{N}
$$
$textbf{(c)}$ From Coulomb’s law the magnitude of the electric force $F_q$ is given by
$$
F_q = kfrac{q^2}{r^2}
$$
with $r = 2.05$ cm. Solving for $q$, we obtain
$$
q = rsqrt{frac{F_q}{k}}
$$
Substituting the known values, we find
$$
begin{align*}
q &= (2.05times10^{-2};mathrm{m})timessqrt{frac{5.0times10^{-4};mathrm{N}}{8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2}}\
&= 4.8;mathrm{nC}
end{align*}
$$
$textbf{(b)}$ $1.5times10^{-3}$ N
$textbf{(c)}$ 4.8 nC
As you walk over a carpet in socks, your feet rub more electrons off the carpet, leaving you with an excessive amount of electric (negative) charge. What happens next when you touch a doorknob is that the excessive negative charge (electrons) stored in your body flows extremely fast and rushes to the knob, which is exactly what make you feel that sting, quick shock.
The exact amount of electric charge transferred during the knob’s shock varies depending on a lot of factors, including how much dry the medium around is and the conductivity of the knob’s material, but the typical value goes about 100 nC. This occurs in a few milliseconds, which is insufficient to cause a current with real damage.
Since the electric force is what causes the electrons to go around the nucleus in orbits with a definite size, we would expect the size of atomic orbits to increase if the electric force were weaker, and we would obtain atoms larger in size.
weaker electric forces mean less tight electrons around the nucleus or in other words, larger atoms
So the number of electrons transferred to produce a charge of $+93.0:pC$ is $dfrac{93 times 10^{-12}}{1.6 times 10^{-19}} = 58.1 times 10^7 = 5.81 times 10^8:electrons$.
Separation between two bees is $d = 1.20:cm = 0.012:m$.
If we consider two bees as two point charges, then the magnitude of the electrostatic force acting between the bees is given by
$F = k dfrac{q^2}{d^2}$
where $k = 8.99 times 10^9:N.m^2. C^{-2}$.
$F = dfrac{8.99 times 10^9 times (93.0 times 10^{-12})^2}{(0.012)^2} = dfrac{8.99 times 93^2}{144} times 10^{-9} = 540 times 10^{-9}:N$
$$
F = 5.40 times 10^{-7}:N
$$
Charge of the pollen is $-93.0 :pC = -93.0 times 10^{-12}:C$.
If we consider them as two point charges then the magnitude of the electrostatic force between them is given by
$F = k dfrac{(93.0 times 10^{-12})^2}{d^2}$
where $k = 8.99 times 10^9 :N.m^2.C^{-2}$ and $d$ is the separation between the bee and the pollen.
This relation can be rewritten for $d$ as
$d = sqrt{dfrac{k}{F}} times 93 times 10^{-12}:m$
If $F = 4.0 times 10^{-8}:N$ then
$d = sqrt{dfrac{8.99 times 10^9}{4.0 times 10^{-8}}} times 93 times 10^{-12} = sqrt{dfrac{89.9}{4.0}} times 93 times 10^{-12} times 10^8 = 441 times 10^{-4}:m$ or
$d = 4.4 :cm$

