
All Solutions
Page 486: Assessment
Since mass is constant everywhere and bath $mc_4k$ are independent of acceleration due to gravity on moon ,
Time period on earth $c_1$ mon are same for mass – spring system.
So the total distance traveled in one oscillation is $4A$ where $A$ is the amplitude.
We conclude that the time needed to traverse $3A$ is actually
$$
begin{equation*}
t = frac{3}{4} cdot T
end{equation*}
$$
For a mass $m$ attached to a spring with a spring constant $k$ we know that the period of simple harmonic oscillations will be:
$$
begin{equation}
T = 2 , pi ; sqrt{frac{m}{k}}
end{equation}
$$
– Masses: $m_{text{A}} = m$ , $m_{text{B}} = 2m$ , $m_{text{C}} = 3m$ , $m_{text{D}} = m$
– Spring constants: $k_{text{A}} = k$ , $k_{text{B}} = k$ , $k_{text{C}} = 6k$ , $k_{text{D}} = 4k$
$$
begin{align*}
T_{text{A}} &= 2 , pi ; sqrt{frac{m}{k}} = T \
T_{text{B}} &= 2 , pi ; sqrt{frac{2m}{k}} = sqrt{2} cdot T \
T_{text{C}} &= 2 , pi ; sqrt{frac{3m}{6k}} = frac{sqrt{2}T}{2}\
T_{text{D}} &= 2 , pi ; sqrt{frac{m}{4k}} = frac{T}{2}\
end{align*}
$$
Now we rank the systems in order of increasing period:
$$
begin{align*}
T_{text{D}} < T_{text{C}} < T_{text{A}} < T_{text{B}}
end{align*}
$$
$$
begin{align*}
D < C < A < B
end{align*}
$$
For a mass $m$ attached to a spring with a spring constant $k$ we know that the period of simple harmonic oscillations will be:
$$
begin{equation}
T = 2 , pi ; sqrt{frac{m}{k}}
end{equation}
$$
We know that period $T$ is defined as the time required to complete one full cycle of a given motion.
The frequency $f$ is the number of oscillations per unit time.
They are related by the following formula:
$$
begin{equation}
f = frac{1}{T}
end{equation}
$$
begin{enumerate}[a)]
item
When the bus takes on more passengers its mass increases, we want to analyze how this effect the frequency of oscillations. \
To find the relation between the mass and the frequency we will combine formulas (1) and (2) as follows:
begin{align*}
frac{1}{f} &= T = 2 , pisqrt{frac{m}{k}} \
frac{1}{f} &= 2 , pi sqrt{frac{m}{k}}
end{align*}
Now inverting for $f$:
begin{align*}
f = frac{1}{2 , pi , sqrt{frac{m}{k}}}
end{align*}
We see that the frequency is inversely proportional to the square of the mass, that is
begin{align*}
f sim frac{1}{sqrt{m}}
end{align*}
So we conclude that an increase in the mass will lead to a decrease in the frequency!
item
Only explanation A is correct.
end{enumerate}
item
When more passengers enter the bus the frequency decreases, that is it is lower than it was before.
item
The correct answer is A.
end{enumerate}
We know that period $T$ is defined as the time required to complete one full cycle of a given motion.
The frequency $f$ is the number of oscillations per unit time.
They are related by the following formula:
$$
begin{equation}
f = frac{1}{T}
end{equation}
$$
The rocking chair completes 12 cycles in 21 seconds, so we can find the frequency directly from the definition as follows:
$$
begin{align*}
f = frac{12text{ cycles}}{21text{ second}} approx 0.57text{ Hz}
end{align*}
$$
The period we find using formula (1):
$$
begin{align*}
T = frac{1}{f} = frac{1}{0.57text{ Hz}} approx 1.75text{ s}
end{align*}
$$
The period is $T = 1.75text{ s}$
We know that period $T$ is defined as the time required to complete one full cycle of a given motion.
The frequency $f$ is the number of oscillations per unit time.
They are related by the following formula:
$$
begin{equation}
f = frac{1}{T}
end{equation}
$$
The bobber is bobbing with a frequency$f = 2.6text{ Hz}$, so we can find the period directly by using formula (1):
$$
begin{align*}
T = frac{1}{f} = frac{1}{2.6text{ Hz}} approx 0.385text{ s}
end{align*}
$$
We know that period $T$ is defined as the time required to complete one full cycle of a given motion.
The frequency $f$ is the number of oscillations per unit time.
They are related by the following formula:
$$
begin{equation}
f = frac{1}{T}
end{equation}
$$
The medical turning fork has a frequency of $f = 128text{ Hz}$, so we can find the period directly by using formula (1):
$$
begin{align*}
T = frac{1}{f} = frac{1}{128text{ Hz}} approx 7.8 cdot 10^{-3}text{ s}
end{align*}
$$
We know that period $T$ is defined as the time required to complete one full cycle of a given motion.
The frequency $f$ is the number of oscillations per unit time.
They are related by the following formula:
$$
begin{equation}
f = frac{1}{T}
end{equation}
$$
We dribble a basketball with a frequency $f = 1.8text{ Hz}$, so we can find the period directly by using formula (1):
$$
begin{align*}
T = frac{1}{f} = frac{1}{1.8text{ Hz}} approx 0.556text{ s}
end{align*}
$$
The time required for 12 dribbles is found simply by multiplying the period:
$$
begin{align*}
t = 12 cdot T = 12 cdot 0.556text{ s} approx 6.7text{ s}
end{align*}
$$
We know that period $T$ is defined as the time required to complete one full cycle of a given motion.
The frequency $f$ is the number of oscillations per unit time.
They are related by the following formula:
$$
begin{equation}
f = frac{1}{T}
end{equation}
$$
We observe 74 heartbeats in a minute, that is in 60 seconds, so we can find the frequency directly from the definition as follows:
$$
begin{align*}
f = frac{74text{ heartbeats}}{60text{ seconds}} = 1.23text{ Hz}
end{align*}
$$
The period we find by using formula (1):
$$
begin{align*}
T = frac{1}{f} = frac{1}{1.23text{ Hz}} approx 0.81text{ s}
end{align*}
$$
The period is $T = 0.81text{ s}$
For a mass $m$ attached to a spring with a spring constant $k$ we know that the period of simple harmonic oscillations will be:
$$
begin{equation}
T = 2 , pi ; sqrt{frac{m}{k}}
end{equation}
$$
When a spring is compressed or pulled by a given force $F$ its elongation $x$ is proportional to that force, and the coefficient is called the spring constant.
This is described by Hooke’s Law:
$$
begin{equation}
F = k , x
end{equation}
$$
begin{enumerate}[a)]
item
The spring constant for this spring can be obtained by looking at the graph. Since this graph represents the relation between the force extending the spring, and its elongation, we can conclude that the slope corresponds to the spring constant. This follows from Hooke’s law, that is formula (2) \\
Reading the coordinates of the furthest point we get:
begin{align*}
k = frac{F}{x} = frac{5text{ N}}{0.25text{ m}} = 20 ; frac{text{N}}{text{m}}
end{align*}
item
The period of oscillation for the spring from part a) and a mass of $m = 0.1text{ kg}$ can be found simply using formula (1) as follows:
begin{align*}
T = 2 , pi sqrt{frac{m}{k}}
end{align*}
Inserting in the values we get
begin{align*}
T = 2 , pi sqrt{frac{0.1text{ kg}}{20 ;frac{text{N}}{text{m}}}} = 0.44text{ s}
end{align*}
end{enumerate}
item
The spring constant of the spring is $k = 20 ; frac{text{N}}{text{m}}$
item
The period of oscillation is $T = 0.44text{ s}$
end{enumerate}
The period of a pendulum oscillating due to gravity can be found using the length of the pendulum $L$ as follows:
$$
begin{equation}
T = 2 , pi sqrt{frac{L}{g}}
end{equation}
$$
– The mass of our spring is $m = 0.46text{ kg}$
– The period of our harmonic motion $T = 0.77text{ s}$
We will use formula (1) to find the spring constant $k$ using the mass of the spring, and the period of the motion.
Rearranging for the spring constant we have:
$$
begin{align*}
T &= 2 , pi ; sqrt{frac{m}{k}} \
T^2 &= (2 , pi)^2 ; frac{m}{k} \
k &= frac{4 , pi^2}{T^2} ; m
end{align*}
$$
Plugging in the values we get:
$$
begin{align*}
k = frac{4 , pi^2}{(0.77text{ s})^2} cdot 0.46text{ kg} approx 30.6 ; frac{text{N}}{text{m}}
end{align*}
$$
We know that the frequency $f$ is the number of oscillations per unit time. This is symbolically written:
$$
begin{equation}
f = frac{n}{t}
end{equation}
$$
begin{enumerate}[a)]
item
Since we know the frequency of our heartbeats to be $f = 1.45text{ Hz}$ we can find the number of beats in a minute directly from formula (1) as follows:
begin{align*}
n = f cdot t = 1.45text{ Hz} cdot 60text{ s} = 87text{ beats}
end{align*}
item
We see that the number of beats is directly proportional to the frequency
begin{align*}
n sim f
end{align*}
So if $f$ increases, so will the number of beats.
item
This is calculated in the same manner as in part a), now only using $f = 1.55text{ Hz}$, that is using formula (1):
begin{align*}
n = f cdot t = 1.55text{ Hz} cdot 60text{ s} =93text{ beats}
end{align*}
end{enumerate}
item
$n = 87text{ beats}$
item
If the frequency increases so will the number of beats
item
$n = 93text{ beats}$
end{enumerate}
For a mass $m$ attached to a spring with a spring constant $k$ we know that the period of simple harmonic oscillations will be:
$$
begin{equation}
T = 2 , pi ; sqrt{frac{m}{k}}
end{equation}
$$
When a spring is compressed or pulled by a given force $F$ its elongation $x$ is proportional to that force, and the coefficient is called the spring constant.
This is described by Hooke’s Law:
$$
begin{equation}
F = k , x
end{equation}
$$
Firstly we use the stretch distance $x = 15text{ cm}$ and the mass $m = 0.5text{ kg}$ attached to the spring, to find the spring constant. We will use formula (2). In our case the force $F$ stretching the spring is the weight of the attached mass $m$.
So we can write:
$$
begin{align*}
m , g = k , x
end{align*}
$$
Rearranging for $k$ we get:
$$
begin{align*}
k = frac{m , g}{x}
end{align*}
$$
Plugging in the values we get:
$$
begin{align*}
k &= frac{0.5text{ kg} cdot 9.81 ; frac{text{m}}{text{s}^2}}{0.15text{ m}} \
k &approx 32.7 ; frac{text{N}}{text{m}}
end{align*}
$$
The mass that needs to be attached to the spring, to result in a period of oscillation of the spring $T = 0.75text{ s}$, can be found simply using formula (1) as follows:
$$
begin{align*}
T = 2 , pi sqrt{frac{m_2}{k}}
end{align*}
$$
Rearranging for $m_2$ we get:
$$
begin{align*}
T^2 &= 4 , pi^2 frac{m_2}{k} \
m_2 &= frac{T^2 , k}{4 , pi^2}
end{align*}
$$
Plugging in the numbers we get:
$$
begin{align*}
m_2 &= frac{(0.75text{ s})^2 cdot 32.7 ; frac{text{N}}{text{m}} }{4 pi^2 } \
m_2 &approx 0.47text{ kg}
end{align*}
$$
We conclude that the pendulum went through the equilibrium position twice!
The period of a pendulum oscillating due to gravity can be found using the length of the pendulum $L$ as follows:
$$
begin{equation}
T = 2 , pi sqrt{frac{L}{g}}
end{equation}
$$
By looking at formula (1) we can see that the period $T$ of the pendulum is proportional to the square root of the length of the pendulum $L$, that is:
$$
begin{align*}
T sim sqrt{L}
end{align*}
$$
We will denote the old and new periods $T_1 = T$ and $T_2 = 3T$ and the old and new lengths $L_1=L$ and $L_2$ is to be found.
Now we write:
$$
begin{align*}
frac{T_2}{T_1} = sqrt{frac{L_2}{L_1}}
end{align*}
$$
Rearranging for $L_2$ we get:
$$
begin{align*}
& left(frac{T_2}{T_1} right)^2 = frac{L_2}{L_1} \
& L_2 = frac{T_2^2 , L_1}{T_1^2} = frac{9T^2 , L}{T^2}\
& L_2 = 9L
end{align*}
$$
The period of a pendulum oscillating due to gravity can be found using the length of the pendulum $L$ as follows:
$$
begin{equation}
T = 2 , pi sqrt{frac{L}{g}}
end{equation}
$$
By looking at formula (1) we can see that the period $T$ of the pendulum is proportional to the square root of the length of the pendulum $L$, that is:
$$
begin{align*}
T sim sqrt{L}
end{align*}
$$
Notice that the period is independent of the mass!
Now we write:
$$
begin{align*}
frac{T_{text{A}}}{T_{text{B}}} = sqrt{frac{L_{text{A}}}{L_{text{B}}}} = sqrt{frac{L}{L}} = 1
end{align*}
$$
The period of a pendulum oscillating due to gravity can be found using the length of the pendulum $L$ as follows:
$$
begin{equation}
T = 2 , pi sqrt{frac{L}{g}}
end{equation}
$$
Pendulum A has smaller amplitude ($10text{textdegree}$) than pendulum B($20text{textdegree}$)
By looking at formula (1) we can see that the period $T$ of the pendulum is proportional to the square root of the length of the pendulum $L$, that is:
$$
begin{align*}
T sim sqrt{L}
end{align*}
$$
Notice that the period is independent of the amplitude!
Now we write:
$$
begin{align*}
frac{T_{text{A}}}{T_{text{B}}} = sqrt{frac{L_{text{A}}}{L_{text{B}}}} = sqrt{frac{L}{L}} = 1
end{align*}
$$
We conclude that both pendulums have the same period, since they have the same length.
This can be understood as follows, even though pendulum B has to move a larger distance than pendulum A it has, in average, greater speed than pendulum A.
The period of a pendulum oscillating due to gravity can be found using the length of the pendulum $L$ as follows:
$$
begin{equation}
T = 2 , pi sqrt{frac{L}{g}}
end{equation}
$$
We know that period $T$ is defined as the time required to complete one full cycle of a given motion.
The frequency $f$ is the number of oscillations per unit time.
They are related by the following formula:
$$
begin{equation}
f = frac{1}{T}
end{equation}
$$
If we consider the metronome to behave as a pendulum, we can analyze what change of length is needed to increase the frequency of a regular pendulum.
By looking at formula (1) we can see that the period $T$ of the pendulum is proportional to the square root of the length of the pendulum $L$, that is:
$$
begin{align*}
T sim sqrt{L}
end{align*}
$$
Now using formula (2) to relate the frequency to the period we get:
$$
begin{align*}
f = frac{1}{T}
end{align*}
$$
Putting these things together we get:
$$
begin{align*}
f sim frac{1}{sqrt{L}}
end{align*}
$$
Meaning the frequency is inversely proportional to the square root of the length of the pendulum.
To increase the frequency, we should shorten the length, this is done by moving the bow tie on the metronome downward.
The period of a pendulum oscillating due to gravity can be found using the length of the pendulum $L$ as follows:
$$
begin{equation}
T = 2 , pi sqrt{frac{L}{g}}
end{equation}
$$
begin{enumerate}[a)]
item
Firstly let us state that when we climb a mountain, the local gravity is a bit weaker then it was when we were at lower heights. Now let us examine how this change effects the period of a grandfather clock. \\
By looking at formula (1) we can see that the period $T$ of the pendulum is inversely proportional to the square root of the gravitational acceleration, that is:
begin{align*}
T sim frac{1}{sqrt{g}}
end{align*}
From this it is obvious that the period will be longer in a place where the gravitational acceleration is weaker. \\
Since the gravitational acceleration is greater at the top of the mountain than it is at sea level we deduce that the period will be longer at the top of the mountain that it is at sea level. \\
This means that the grandfather clock will take longer to count each second that it actually should. This will lead to it running slower.
item
The correct explanation is A
end{enumerate}
item
The clock will run slower than it should
item
The correct explanation is A
end{enumerate}
The period of a pendulum oscillating due to gravity can be found using the length of the pendulum $L$ as follows:
$$
begin{equation}
T = 2 , pi sqrt{frac{L}{g}}
end{equation}
$$
We know that period $T$ is defined as the time required to complete one full cycle of a given motion.
The frequency $f$ is the number of oscillations per unit time.
They are related by the following formula:
$$
begin{equation}
f = frac{1}{T}
end{equation}
$$
To find the period of the pendulum we will use the given frequency $f = 0.24text{ Hz}$, along with the formula (2), this gives us:
$$
begin{align*}
T = frac{1}{0.24text{ Hz}} approx 4.17text{ s}
end{align*}
$$
Now to find the length of the pendulum we use formula (1):
$$
begin{align*}
T = 2 , pi ; sqrt{frac{L}{g}}
end{align*}
$$
Rearranging for $L$ we get:
$$
begin{align*}
T^2 &= 4 , pi^2 ; frac{L}{g} \
L &= frac{T^2 , g}{4 , pi^2}
end{align*}
$$
Plugging in the numbers for $T$ and $g$ we get:
$$
begin{align*}
L &= frac{(4.17text{ s})^2 , 9.81 ; frac{text{m}}{text{s}^2}}{4 , pi^2 } approx 4.33text{ m}
end{align*}
$$
The period of a pendulum oscillating due to gravity can be found using the length of the pendulum $L$ as follows:
$$
begin{equation}
T = 2 , pi sqrt{frac{L}{g}}
end{equation}
$$
We know that period $T$ is defined as the time required to complete one full cycle of a given motion.
The frequency $f$ is the number of oscillations per unit time.
They are related by the following formula:
$$
begin{equation}
f = frac{1}{T}
end{equation}
$$
The pendulum completes 13 cycles in 110 seconds, so we can find the frequency directly from the definition as follows:
$$
begin{align*}
f = frac{13text{ cycles}}{110text{ seconds}} approx 0.12text{ Hz}
end{align*}
$$
To find the period of the pendulum we will use the frequency $f = 0.12text{ Hz}$, along with the formula (2), this gives us:
$$
begin{align*}
T = frac{1}{0.12text{ Hz}} approx 8.33text{ s}
end{align*}
$$
Now to find the length of the pendulum we use formula (1):
$$
begin{align*}
T = 2 , pi ; sqrt{frac{L}{g}}
end{align*}
$$
Rearranging for $L$ we get:
$$
begin{align*}
T^2 &= 4 , pi^2 ; frac{L}{g} \
L &= frac{T^2 , g}{4 , pi^2}
end{align*}
$$
Plugging in the numbers for $T$ and $g$ we get:
$$
begin{align*}
L &= frac{(8.33text{ s})^2 , 9.81 ; frac{text{m}}{text{s}^2}}{4 , pi^2 } approx 17.26text{ m}
end{align*}
$$
The period of a pendulum oscillating due to gravity can be found using the length of the pendulum $L$ as follows:
$$
begin{equation}
T = 2 , pi sqrt{frac{L}{g}}
end{equation}
$$
The pendulum completes 5 swings in 16 seconds, so we can find the period directly from the definition as follows:
$$
begin{align*}
T = frac{16text{ seconds}}{5} = 3.2text{ s}
end{align*}
$$
Now to find the gravitational acceleration of the pendulum we use formula (1) and the value for length of the pendulum $L = 2.5text{ m}$:
$$
begin{align*}
T = 2 , pi ; sqrt{frac{L}{g}}
end{align*}
$$
Rearranging for $g$ we get:
$$
begin{align*}
& T^2 = 4 , pi^2 ; frac{L}{g} \
& g = frac{4 , pi^2 , L}{T^2}
end{align*}
$$
Plugging in the numbers for $T$ and $L$ we get:
$$
begin{align*}
g = frac{4 , pi^2 , 2.5text{ m}}{(3.2text{ s})^2} approx 9.63 ; frac{text{m}}{text{s}^2}
end{align*}
$$
The period of a pendulum oscillating due to gravity can be found using the length of the pendulum $L$ as follows:
$$
begin{equation}
T = 2 , pi sqrt{frac{L}{g}}
end{equation}
$$
To find the length of the pendulum we use formula (1):
$$
begin{align*}
T = 2 , pi sqrt{frac{L}{g}}
end{align*}
$$
Rearranging for $L$ we get:
$$
begin{align*}
& T^2 = 4 , pi^2 ; frac{L}{g} \
& L = frac{T^2 , g}{4 , pi^2}
end{align*}
$$
Plugging in the numbers for $T=2text{ s}$ and $g = 9.81 ; frac{text{m}}{text{s}^2}$ we get:
$$
begin{align*}
L = frac{(2text{ s})^2 , 9.81 ; frac{text{m}}{text{s}^2} }{4 , pi^2 } approx 1text{ m}
end{align*}
$$
The period of a pendulum oscillating due to gravity can be found using the length of the pendulum $L$ as follows:
$$
begin{equation}
T = 2 , pi sqrt{frac{L}{g}}
end{equation}
$$
begin{enumerate}[a)]
item
One full oscillation consists of motion from the equilibrium to the first amplitude (maximal displacement), then back to the equilibrium, then to the other amplitude position, and then finally back to the equilibrium. \\
So the total motion consist of two equilibrium to equilibrium cycles, so the period of our pendulum is two times greater than the time between consecutive equilibrium positions. So we find:
begin{align*}
T = 2 cdot t = 2 cdot 1text{ s} = 2text{ s}
end{align*}
item
Now to find the gravitational acceleration of the pendulum we use formula (1) and the value for length of the pendulum $L=0.9933text{ m}$:
begin{align*}
T = 2 , pi sqrt{frac{L}{g}}
end{align*}
Rearranging for $g$ we get:
begin{align*}
& T^2 = 4 , pi^2 ; frac{L}{g} \
& g = frac{4 , pi^2 , L}{T^2}
end{align*}
Plugging in the numbers for $T$ and $L$ we get:
begin{align*}
g = frac{4 , pi^2 , 0.9933text{ m}}{(2text{ s})^2} approx 9.79 ; frac{text{m}}{text{s}^2}
end{align*}
end{enumerate}
item
The period of the pendulum is $T = 2text{ s}$
item
The gravitational acceleration is $g = 9.79 ; frac{text{m}}{text{s}^2}$
end{enumerate}
The period of a pendulum oscillating due to gravity can be found using the length of the pendulum $L$ as follows:
$$
begin{equation}
T = 2 , pi sqrt{frac{L}{g}}
end{equation}
$$
One full oscillation consists of motion from the first amplitude (maximal displacement) to the equilibrium, then to the other amplitude position, and then back to the equilibrium, and finally back to the first amplitude.
So the motion from the amplitude to the equilibrium is actually one fourth of the whole period.
Now to find the period of the pendulum we use formula (1):
$$
begin{align*}
T = 2 , pi sqrt{frac{L}{g}}
end{align*}
$$
Plugging in the numbers for $L = 22.9text{ m}$ and $g = 9.81 ; frac{text{m}}{text{ s}^2}$ we get:
$$
begin{align*}
T = 2 , pi ; sqrt{frac{22.9text{ m}}{9.81 ; frac{text{m}}{text{s}^2}}} approx 9.6text{ s}
end{align*}
$$
Finally, as stated before the time required is:
$$
begin{align*}
t = frac{T}{4} = 2.4text{ s}
end{align*}
$$
The period of a pendulum oscillating due to gravity can be found using the length of the pendulum $L$ as follows:
$$
begin{equation}
T = 2 , pi sqrt{frac{L}{g}}
end{equation}
$$
The pendulum completes 10 cycles in 60 seconds, so we can find the period directly from the definition as follows:
$$
begin{align*}
T = frac{60text{ seconds}}{10text{ cycles}} = 6text{ s}
end{align*}
$$
Now to find the length of the pendulum we use formula (1):
$$
begin{align*}
T = 2 , pi sqrt{frac{L}{g}}
end{align*}
$$
Rearranging for $L$ we get:
$$
begin{align*}
& T^2 = 4 , pi^2 ; frac{L}{g} \
& L = frac{T^2 , g}{4 , pi^2}
end{align*}
$$
Plugging in the numbers for $T$ and $g$ we get:
$$
begin{align*}
L = frac{(6text{ s})^2 , 9.81 ; frac{text{m}}{text{s}^2} }{4 , pi^2 } approx 8.95text{ m}
end{align*}
$$
So we conclude that the height of the radio booth is the same as the length of the pendulum:
$$
begin{align*}
h = L = 8.95text{ m}
end{align*}
$$
Having this in mind, one can conclude that since the speed of the wave is constant with the passage of time, the time needed for the wave to travel two wavelengths will be twice as large, that is:
$$
begin{align*}
t = 2 cdot T
end{align*}
$$
We know that the wavelength and frequency determine the speed of a wave. They are related by the following formula:
$$
begin{equation}
v = lambda cdot f
end{equation}
$$
We know that red light has higher wavelength than violet light, so we can write:
$$
begin{align*}
lambda_r > lambda_v
end{align*}
$$
We also know that the speed of both waves are the same so we write:
$$
begin{align*}
v_r = v_v
end{align*}
$$
Now using formula (1) we find the frequencies of both waves:
$$
begin{align*}
f_r & = frac{v_r}{lambda_r} \
f_v &= frac{v_v}{lambda_v}
end{align*}
$$
Since the speeds are the same, and the wavelength of red light is greater, we conclude that its frequency will be smaller.
That is, violet light will have the higher frequency of the two.
In the case of a baseball game, the creation of this wave would require the moving of the bodies of the fans in the following manner:
Firstly all the fans would need to be standing up, then one fan, who was standing near seat 1 would walk over to the sit next to him, which we will call seat 2.
Then the fan that was located at seat 2 would go over to seat 3.
And so on, and so forth, the fans would all move to the seats adjacent their initial seats.
Then we will remember from the theory, that a longitudinal wave is characterized by the fact that the particles that make up the wave, and the wave itself, are moving in parallel directions.
We know that the wavelength and frequency determine the speed of a wave. They are related by the following formula:
$$
begin{equation}
v = lambda cdot f
end{equation}
$$
begin{enumerate}[a)]
item
The frequency of a wave can be determined by looking at how densely the antinodes are packed together. The closer they are the greater the frequency. Looking at the pictures we get:
begin{align*}
f_{text{B}} < f_{text{C}} < f_{text{A}}
end{align*}
item
Now using the fact that the waves have the same speed, along with equation (1) we conclude that the wavelengths are arranged in the inverse order:
begin{align*}
lambda_{text{A}} < lambda_{text{C}} < lambda_{text{B}}
end{align*}
Notice that the same result could have been obtained by first ordering the wavelengths, and the inverting the order for frequencies. The order for wavelengths could have been found by looking at the distance between neighboring nodes for each eave, and remembering that said distance is actually one half of the wavelength in question.
end{enumerate}
item
$ f_{text{B}} < f_{text{C}} < f_{text{A}} $
item
$ lambda_{text{A}} < lambda_{text{C}} < lambda_{text{B}} $
end{enumerate}
We know that period $T$ is defined as the time required to complete one full cycle of a given motion.
The frequency $f$ is the number of oscillations per unit time.
They are related by the following formula:
$$
begin{equation}
f = frac{1}{T}
end{equation}
$$
We know that the wavelength and frequency determine the speed of a wave. They are related by the following formula:
$$
begin{equation}
v = lambda cdot f
end{equation}
$$
We dip our fingers into the pond twice a second, knowing this the frequency can be calculated directly by definition:
$$
begin{align*}
f = frac{n}{t}=frac{2text{ dips}}{1text{ second}}= 2text{ Hz}
end{align*}
$$
Now using formula (1) we can calculate the period:
$$
begin{align*}
T = frac{1}{f} = frac{1}{2text{ Hz}} = 0.5text{ s}
end{align*}
$$
Since we know that the crests of our waves are separated by $0.18text{ m}$, and recognizing this distance as the wavelength by definition we conclude:
$$
begin{align*}
lambda = 0.18text{ m}
end{align*}
$$
Now, knowing the frequency and wavelength of the wave we find its speed using formula (2) as follows:
$$
begin{align*}
v = lambda cdot f = 0.18text{ m} cdot 2text{ Hz} = 0.36 ; frac{text{m}}{text{s}}
end{align*}
$$
The period $T = 0.5text{ s}$
The wavelength $lambda = 0.18text{ m}$
The speed of the wave $v = 0.36 ; frac{text{m}}{text{s}}$
item
We know that for the given wave, the horizontal distance from its crest to the next trough is $28text{ cm}$. \
This is half the distance from crest to crest, for which we know is equal to a wavelength, so we conclude:
begin{align*}
lambda=2 cdot 28text{ cm}=56text{ cm}
end{align*}
item
Now looking at the vertical distance from crest to trough we can find the amplitude of the wave. Since said distance is actually two amplitudes, we can write:
begin{align*}
2A = 13text{ cm} \
A = 6.5text{ cm}
end{align*}
end{enumerate}
item
The wavelength is $lambda = 56text{ cm}$
item
The amplitude is $A = 2.5text{ cm}$
end{enumerate}
Wavelength of these waves $(lambda)=(34)m$
So, speed of the waves,$quad v=lambdamathcal V=((34)(0.23))m/s$
$$
Rightarrowquadboxed{v=(7.8)m/s}
$$
(7.8)m/s
$$
We know that the wavelength and frequency determine the speed of a wave. They are related by the following formula:
$$
begin{equation}
v = lambda cdot f
end{equation}
$$
We know that for our tsunami the speed of the wave is:
$$
begin{align*}
v = 750 ; frac{text{km}}{text{h}}
end{align*}
$$
And its wavelength is:
$$
begin{align*}
lambda = 310text{ km}
end{align*}
$$
Since we now know the wavelength, and we know the speed, the frequency of the wave can be determined using formula (1) as follows:
$$
begin{align*}
v &= lambda cdot f \
f &= frac{v}{lambda}
end{align*}
$$
Plugging in the numbers we get:
$$
begin{align*}
f = frac{750 ; frac{text{km}}{text{h}} }{310text{ km} } = frac{frac{750,000text{ m}}{3600text{ s} }}{310,000text{ m}} approx 6.7 cdot 10^{-4}text{ Hz}
end{align*}
$$
Wavelength ,$quadlambda_1=(1.5)m$
At shallower part of lake : speed of wave ,$quad v_2=(1.6)m/s$
Wavelength ,$quadlambda_2=?$
Frequency of waves remain the same.
So, as$quad v=lambdanuquad$and $nu$ is constant :
$dfrac{v_1}{lambda_1}=dfrac{v_2}{lambda_2}quadRightarrowquadlambda_2=lambda_1(dfrac{v_2}{v_1})=Big[(1.5)big(dfrac{1.6}{2.6}big)Big]m$
$$
Rightarrowquadboxed{lambda_2=(1.2)m}
$$
We know that period $T$ is defined as the time required to complete one full cycle of a given motion.
The frequency $f$ is the number of oscillations per unit time.
They are related by the following formula:
$$
begin{equation}
f = frac{1}{T}
end{equation}
$$
### Theoretical reminder
We know that the wavelength and frequency determine the speed of a wave. They are related by the following formula:
$$
begin{equation}
v = lambda cdot f
end{equation}
$$
begin{enumerate}[a)]
item
We observe that $n = 11$ waves go by us in $t = 45text{ s}$, knowing this the period can be calculated directly by definition:
begin{align*}
T = frac{t}{n} = frac{45text{ s}}{11} approx 4.1 text{ s}
end{align*}
item
Now using formula (1) we can calculate the frequency:
begin{align*}
f = frac{1}{T} = frac{1}{4.1text{ s}} approx 0.24text{ Hz}
end{align*}
item
We know that for the given wave, the horizontal distance from its crest to the next trough is $3text{ m}$. \
This is half the distance from crest to crest, for which we know is equal to a wavelength, so we conclude:
begin{align*}
lambda = 2 cdot 3text{ m} = 6text{ m}
end{align*}
item
Now, knowing the frequency and wavelength of the wave we find its speed using formula (2) as follows:
begin{align*}
v = lambda cdot f = 6text{ m} cdot 0.24text{ Hz} = 1.44 ; frac{text{m}}{text{s}}
end{align*}
end{enumerate}
item
The period $T = 4.1text{ s}$
item
The frequency $f = 0.24text{ Hz}$
item
The wavelength $ lambda = 6text{ m} $
item
The speed of the wave $v = 1.44 ; frac{text{m}}{text{s}} $
end{enumerate}
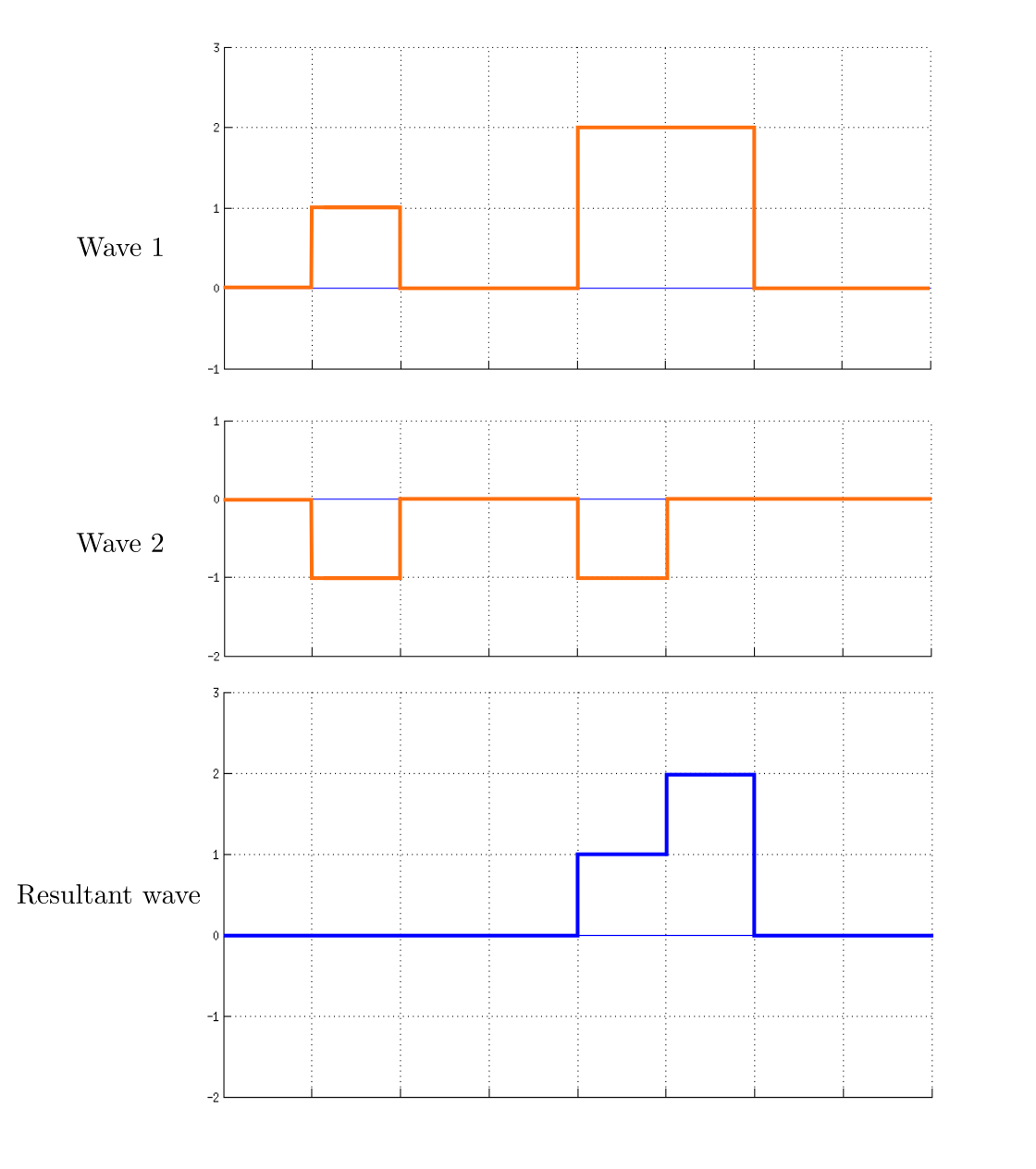
Knowing these things, we see that the blue wave is NOT a simple harmonic wave. It has two different amplitudes, a smaller one in the middle of the graph, and a larger one closer to the edges. Thus we conclude that it was formed by the superposition of the red and green waves, that is, it is the resultant of the other two.
We know that when a standing wave is formed in a string the number of antinodes determines the harmonic of the wave. This gives us a result that the length of the string is equal to a integer number of wavelength halves, that is:
$$
begin{align*}
L = frac{n cdot lambda}{2}
end{align*}
$$
Since the length of the string is $L = 1text{ m}$ we get:
$$
begin{gather*}
2 cdot L = 2 cdot 1text{ m} = 2text{ m} = n cdot lambda \
lambda = frac{2text{ m}}{n}tag{ 1}
end{gather*}
$$
From this we see that any wavelength lambda that fulfils this equation for an integer $n$ can produce a standing wave.
begin{enumerate}[a)]
item
In the problem we are given three lowest frequency standing waves with frequencies
begin{align*}
f_1 = 100text{ Hz}text{ , } f_2 = 200text{ Hz}text{ , } f_3 = 300text{ Hz}
end{align*}
The fundamental frequency is actually the frequency of the first harmonic. That is the frequency of the harmonic whose wavelength is maximal. Its frequency is therefore minimal. Of our three standing waves, the frequency $f_1 = 100text{ Hz}$ belongs to the first (fundamental) harmonic.
item
Because the wavelength of the fundamental harmonic is the maximal wavelength, it is found using formula (1) for the value of the integer $n = 1$:
begin{align*}
lambda = frac{2text{ m}}{1} = 2text{ m}
end{align*}.
end{enumerate}
item
The fundamental frequency is $f = 100text{ Hz}$
item
The fundamental wavelength is $ lambda = 2text{ m}$
end{enumerate}
$$
begin{align*}
v & = 32 mathrm{m/s}
end{align*}
$$
The fundamental frequency for the string is given as
$$
begin{align*}
f_0 & = 65 mathrm{Hz}
end{align*}
$$
The wavelength of the wave is estimated as
$$
begin{align*}
lambda_0 & = dfrac{v}{f_0} \
lambda_0 & = left(dfrac{32}{65}right) mathrm{m}
end{align*}
$$
As shown in the given figure, the string is tied at both ends. Therefore, the wavelength of the fundamental mode is given as
$$
begin{align*}
lambda_0 & = 2, L \
implies L & = dfrac{lambda_0}{2} \
L & = left(dfrac{1}{2}right)cdot left(dfrac{32}{65} right) \
L & = left(dfrac{16}{65} right) mathrm{m} \
L & = 0.246 mathrm{m} \
& hspace*{-4mm}boxed{L = 0.25 mathrm{m} }
end{align*}
$$
Therefore, the length of the string is $displaystyle L=0.25$ m.

We know that the wavelength and frequency determine the speed of a wave. They are related by the following formula:
$$
begin{equation}
v = lambda cdot f
end{equation}
$$
We know that when a standing wave is formed in a string the number of antinodes determines the harmonic of the wave. This gives us a result that the length of the string is equal to a integer number of wavelength halves, that is:
$$
begin{align*}
L = frac{n cdot lambda}{2}
end{align*}
$$
Rearranging gives:
$$
begin{gather*}
2 cdot L = n cdot lambda \
lambda = frac{2L}{n} tag{2}
end{gather*}
$$
From this we see that any wavelength lambda that fulfils this equation for an integer $n$ can produce a standing wave.
The first harmonic is the one with maximal wavelength. Knowing this we set the integer $n = 1$, and since we know the length of the string to be equal $L = 0.83text{ m}$, we find the wavelength of the standing wave using formula (2) as follows:
$$
begin{align*}
lambda = frac{2L}{n} = frac{2 cdot 0.83text{ m}}{1} = 1.66text{ m}
end{align*}
$$
Now we have found the wavelength, and since we know the frequency to be $f = 26text{ Hz}$ we use formula (1) to find the speed of the wave:
$$
begin{align*}
v = lambda cdot f
end{align*}
$$
Plugging in the numbers we get:
$$
begin{align*}
v = 1.66text{ m} cdot 26text{ Hz} approx 43 ; frac{text{m}}{text{s}}
end{align*}
$$
We know that the wavelength and frequency determine the speed of a wave. They are related by the following formula:
$$
begin{equation}
v = lambda cdot f
end{equation}
$$
We know that when a standing wave is formed in a string the number of antinodes determines the harmonic of the wave. This gives us a result that the length of the string is equal to a integer number of wavelength halves, that is:
$$
begin{align*}
L = frac{n cdot lambda}{2}
end{align*}
$$
Rearranging:
$$
begin{gather*}
2 cdot L = n cdot lambda \
lambda = frac{2L}{n}tag{ 2}
end{gather*}
$$
From this we see that any wavelength lambda that fulfils this equation for an integer n can produce a standing wave.
begin{enumerate}[a)]
item
The first harmonic is the one with maximal wavelength. Knowing this we set the integer $n = 1$, and from formula (2) get:
begin{align*}
lambda = 2 cdot L
end{align*}
Now to relate the length with the frequency we use formula (1), keeping in mind that the speed of the waves is constant.
begin{align*}
f = frac{v}{lambda} = frac{v}{2L} tag{3}
end{align*}
From this we conclude that the frequency and length are inversely proportional:
begin{align*}
f sim frac{1}{L}
end{align*}
So, as the length increases, the frequency decreases.
item
Looking at formula (3) we see that the product of the frequency $f$ and length $L$ is constant:
begin{align*}
f cdot L = text{ const}
end{align*}
So, equating this before and after the lengthening of the string we get:
begin{align*}
f_1 cdot L_1 = f_2 cdot L_2
end{align*}
Rearranging we get:
begin{align*}
f_2 = f_1 frac{L_1}{L_2}
end{align*}
Plugging in the numbers we get:
begin{align*}
f_2 &= 41text{ Hz} cdot frac{0.64text{ m}}{0.88text{ m}} \
f_2 &approx 30text{ Hz}
end{align*}
end{enumerate}
item
If the length is increased, the frequency decreases
item
The new frequency is $f_2 = 30text{ Hz}$
end{enumerate}
$$
begin{align*}
v_1 & = 1.0 mathrm{m/s} \
v_2 & = -1.0 mathrm{m/s}
end{align*}
$$
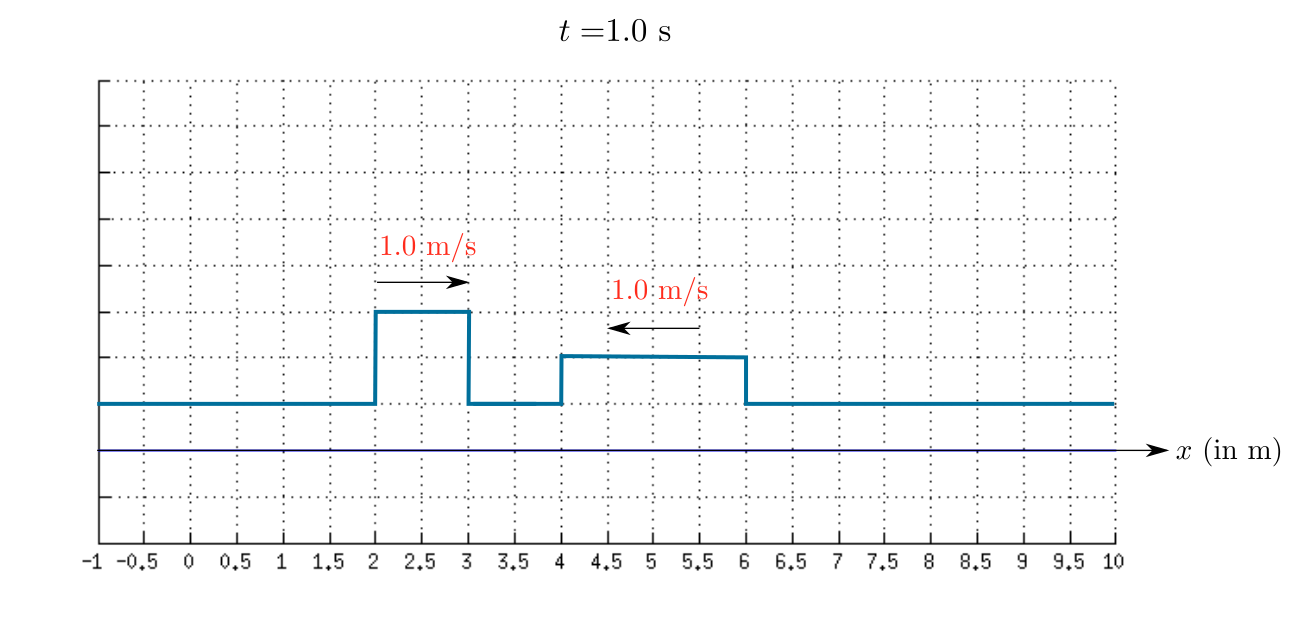
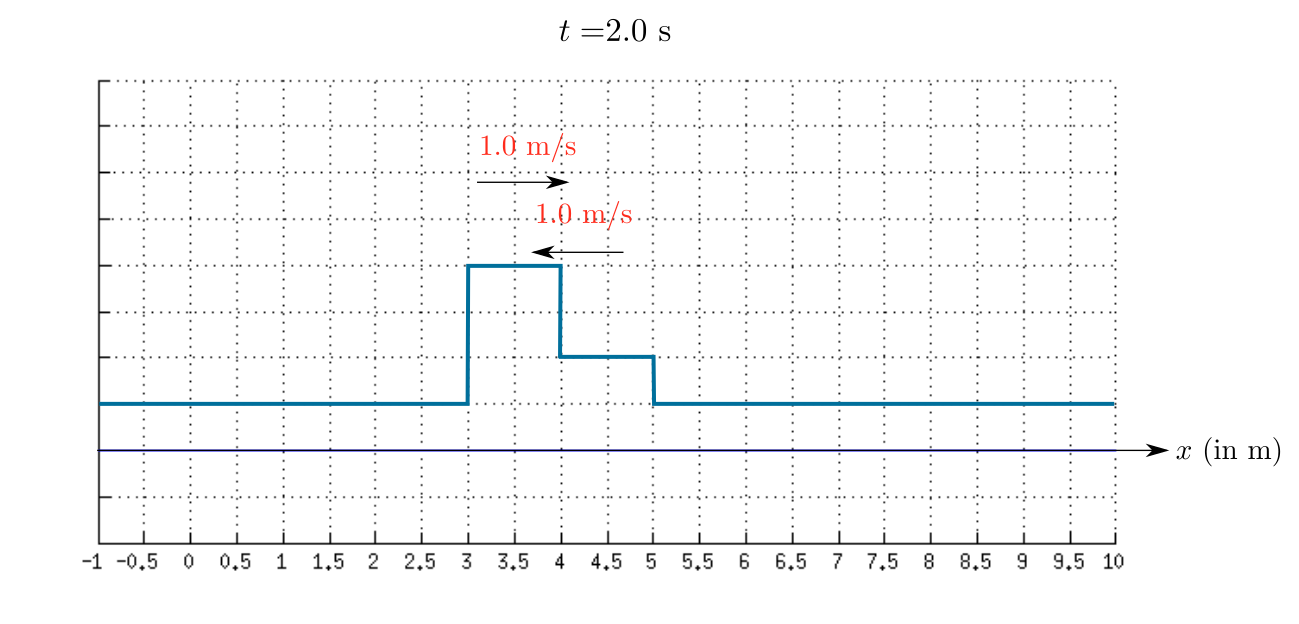
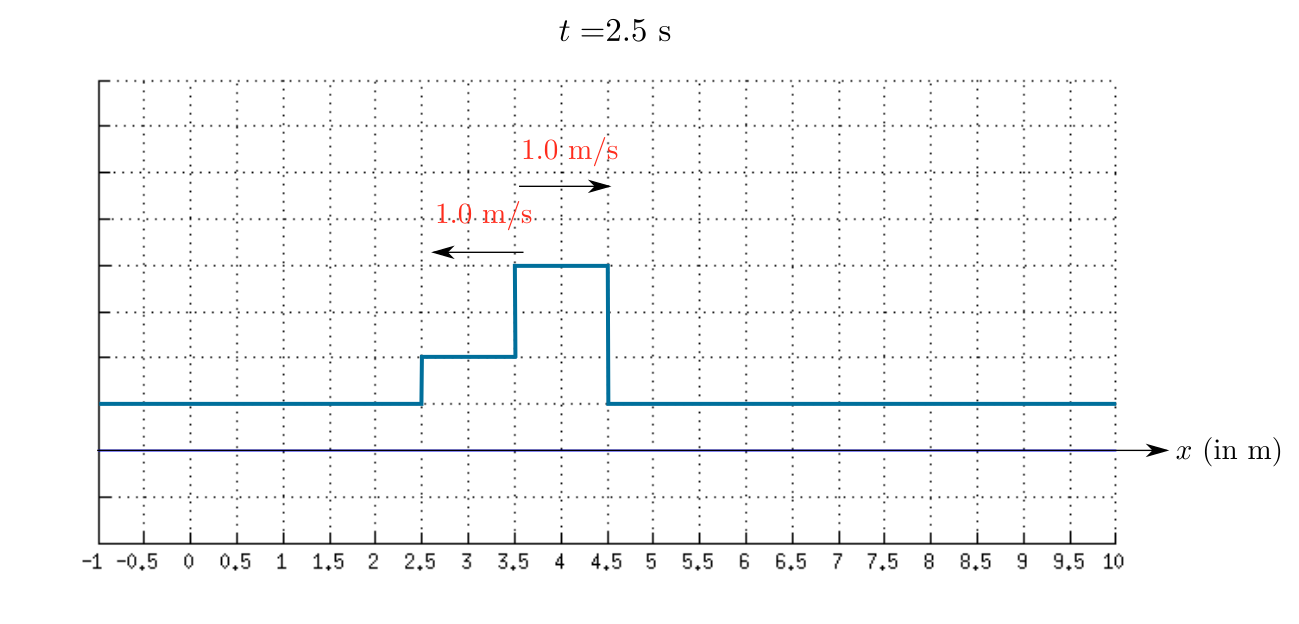
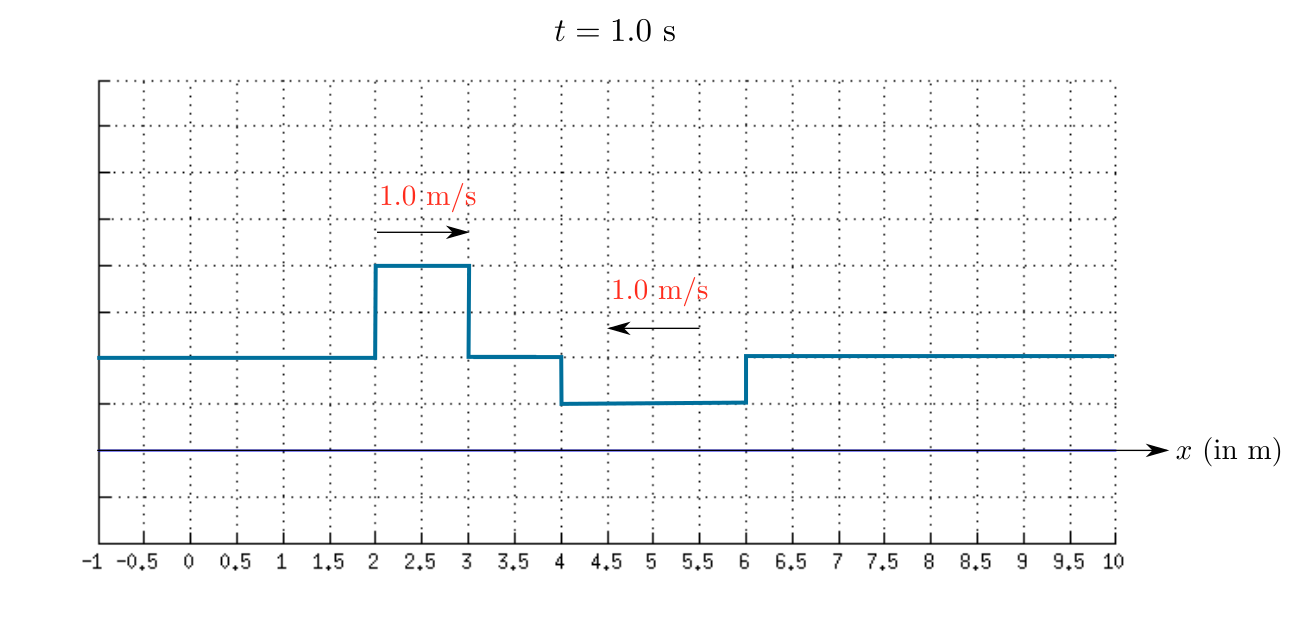
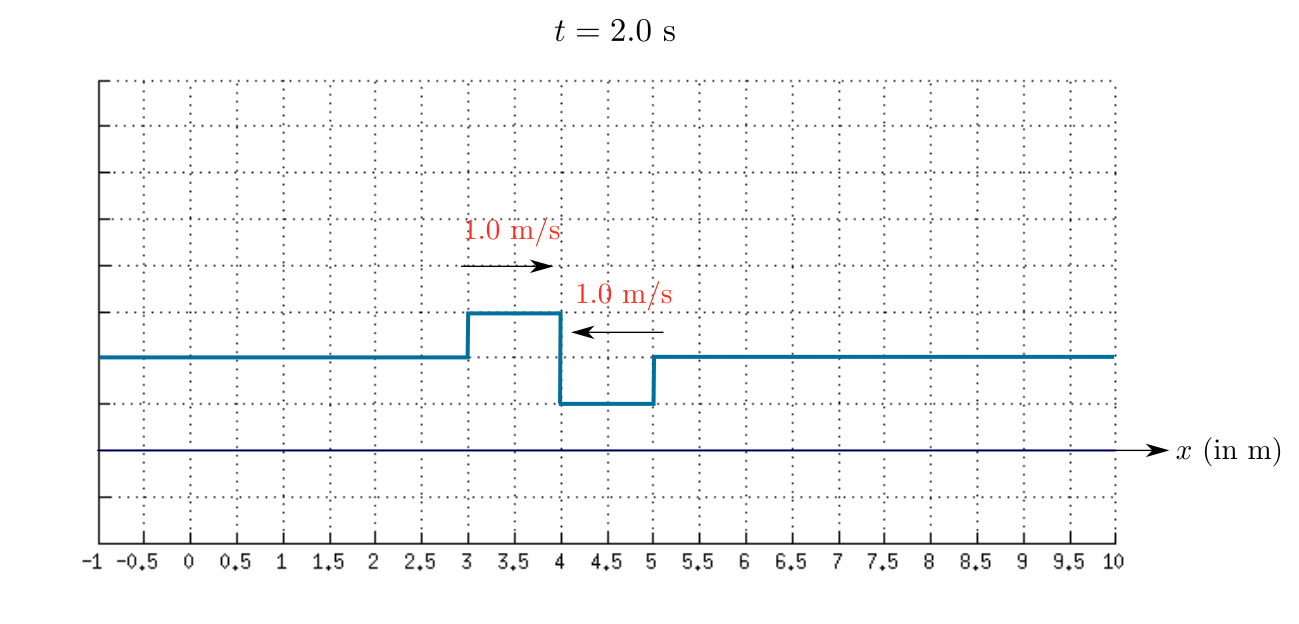
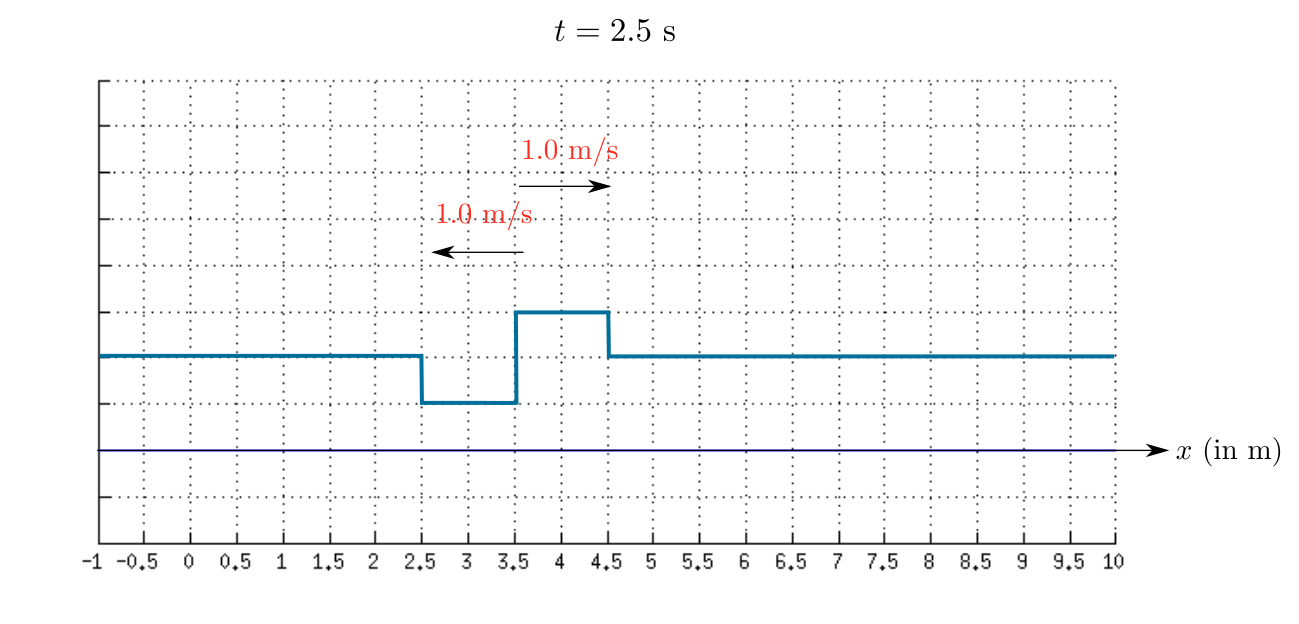
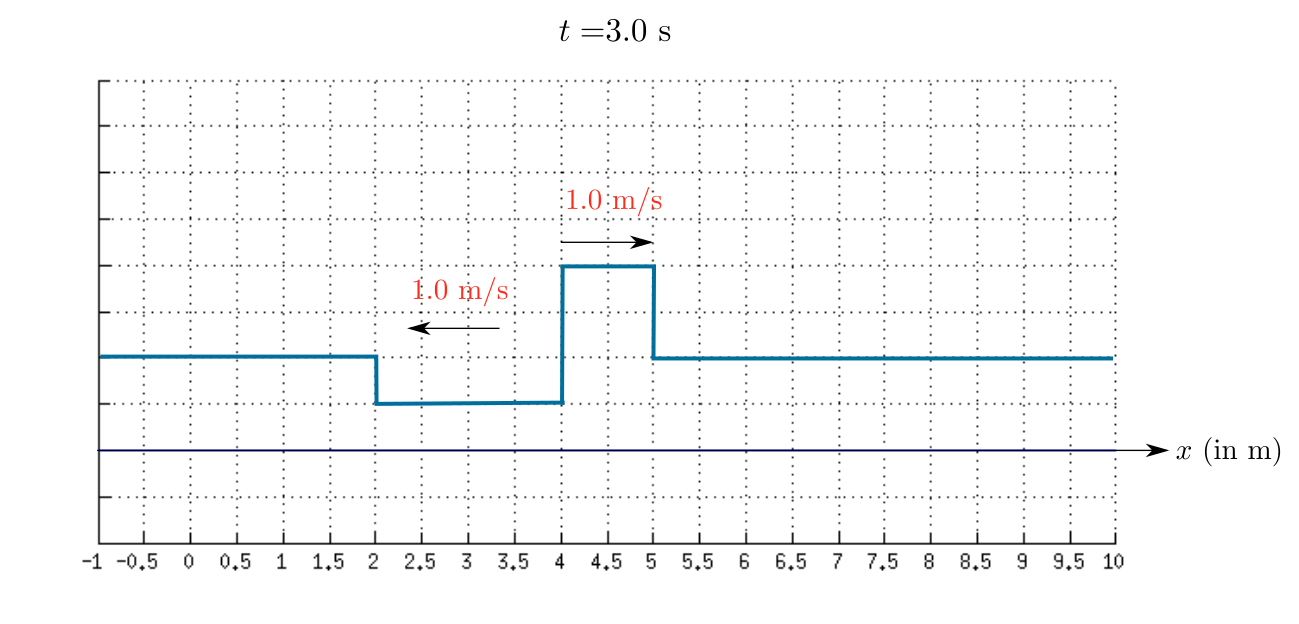
As time passes the first wave move towards right and the second wave move towards left.
Therefore, the sketch of the resultant wave at $t=1.0$ s is shown in the given figure.
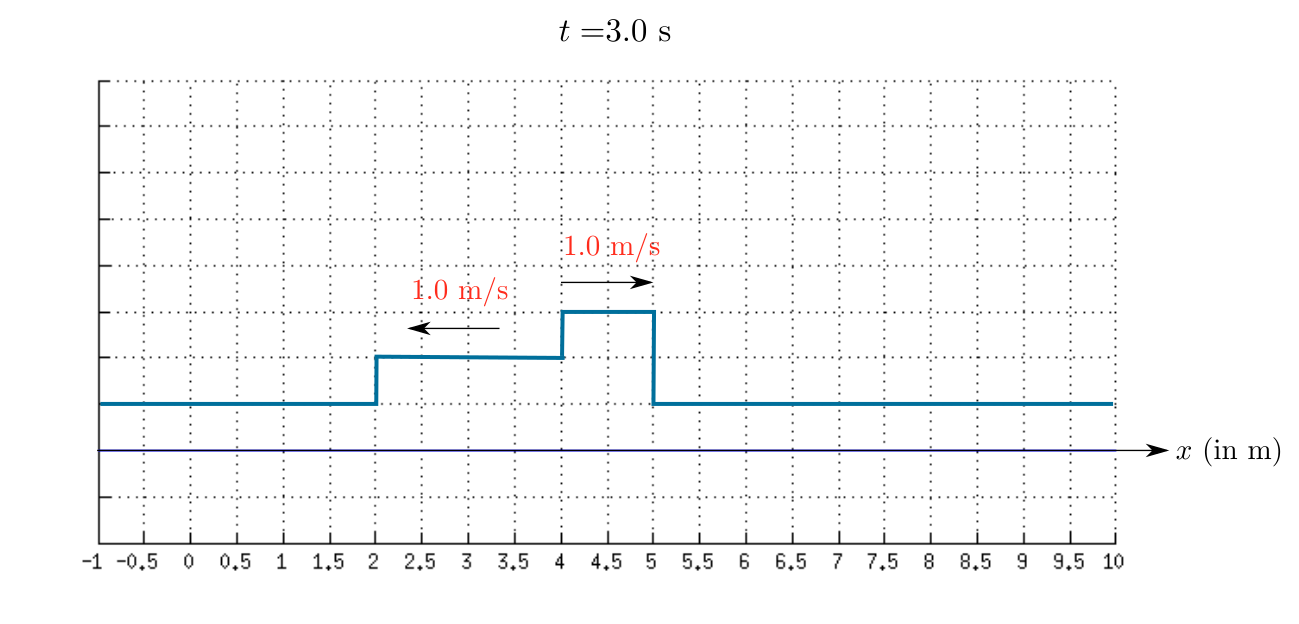
$$
begin{align*}
v_1 & = 1.0 mathrm{m/s} \
v_2 & = -1.0 mathrm{m/s}
end{align*}
$$
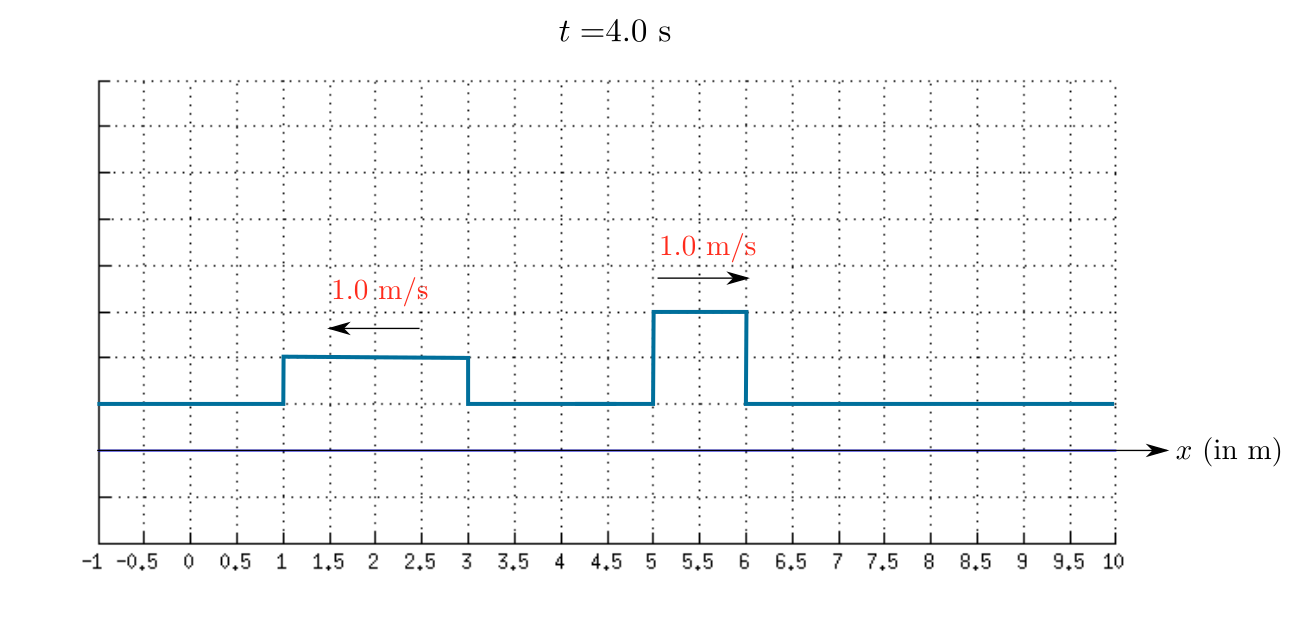
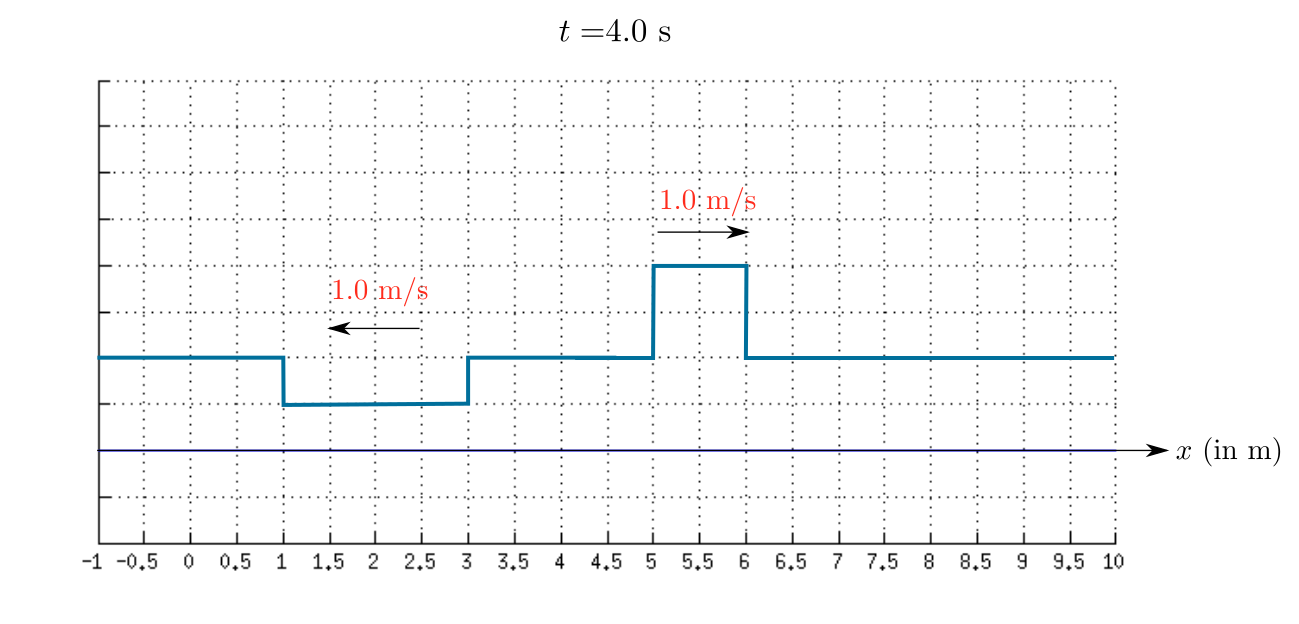
As time passes the first wave (positive pulse) move towards right and the second wave (inverted pulse) move towards left.
Therefore, the sketch of the resultant wave at $t=1.0$ s is shown in the given figure.
We know that when a standing wave is formed in a string the number of antinodes determines the harmonic of the wave. This gives us a result that the length of the string is equal to a integer number of wavelength halves, that is:
$$
begin{align*}
L = frac{n cdot lambda}{2}
end{align*}
$$
Rearranging gives:
$$
begin{align*}
& 2 cdot L = n cdot lambda \
& lambda = frac{2L}{n}tag{1}
end{align*}
$$
From this we see that any wavelength lambda that fulfils this equation for an integer n can produce a standing wave.
begin{enumerate}[a)]
item
We know that the wave in question has 3 antinodes, this means we can recognize it as the third harmonic by definition.
item
The third harmonic is the one with the integer $n = 3$, and since we know the length of the string to be equal $L = 0.66text{ m}$, we find the wavelength of the standing wave using formula (1) as follows:
begin{align*}
lambda = frac{2L}{n} = frac{2 cdot 0.66text{ m}}{3} = 0.44text{ m}
end{align*}
end{enumerate}
item
The third harmonic is in question
item
The wavelength is found to be $lambda = 0.44text{ m}$
end{enumerate}
In our problem the period of the pendulum is $T = 2text{ s}$.
If the pendulum traverses a distance of 4A in one period, then it will traverse 6A in the time
$$
begin{align*}
t = 3text{ s} = frac{3}{2} cdot T
end{align*}
$$
So we can write:
$$
begin{align*}
24text{ cm} = 0.24text{ m} = 6A
end{align*}
$$
We find:
$$
begin{align*}
text{A} = frac{0.24text{ m}}{6} = 0.04text{ m}
end{align*}
$$
For a mass $m$ attached to a spring with a spring constant $k$ we know that the period of simple harmonic oscillations will be:
$$
begin{equation}
T = 2 , pi ; sqrt{frac{m}{k}}
end{equation}
$$
The spring constant of our spring is $k = 2600 ; frac{text{N}}{text{m}}$
The period of our harmonic motion $T = 0.85text{ s}$
We will use formula (1) to find the mass $m$ of our spring using the spring constant $k$ of the spring, and the period of the motion.
Rearranging for the mass we have:
$$
begin{align*}
T &= 2 , pi ; sqrt{frac{m}{k}} \
T^2 &= left(2 , pi right)^2 ; frac{m}{k} \
m &= frac{T^2}{(2 , pi)^2} ; k
end{align*}
$$
Plugging in the values we get:
$$
begin{align*}
m = frac{(0.85text{ s})^2 }{4 , pi^2 } cdot 2600 ; frac{text{N}}{text{m}} approx 48text{ kg}
end{align*}
$$
We know that period $T$ is defined as the time required to complete one full cycle of a given motion.
The frequency $f$ is the number of oscillations per unit time.
They are related by the following formula:
$$
begin{equation}
f = frac{1}{T}
end{equation}
$$
We know that the sunspot activity exhibits a 11 year cycle. This is the period of the oscillating motion. To find the frequency in Hz we need to convert the period to seconds. One year has 365 days, one day has 24 hours, each hour has 3600 seconds, so we can write:
$$
begin{align*}
T = 11 text{ years}
=11 cdot 365 text{ days}
=11 cdot 365 cdot 24 text{ hours}
=11 cdot 356 cdot 24 cdot 3600 text{ seconds}
end{align*}
$$
$$
begin{align*}
T = 346,896,000text{ s} approx 3.47 cdot 10^8text{ s}
end{align*}
$$
Now we find the frequency directly from definition (1) as follows:
$$
begin{align*}
f = frac{1}{T} = frac{1}{ left(3.47 cdot 10^{8}text{ s} right)} = 2.88 cdot 10^{-9}text{ Hz}
end{align*}
$$
We know that period $T$ is defined as the time required to complete one full cycle of a given motion.
The frequency $f$ is the number of oscillations per unit time.
They are related by the following formula:
$$
begin{equation}
f = frac{1}{T}
end{equation}
$$
We know that the vibrations on the surface of the sun have a $5.7text{ min}$ period. To find the frequency in Hz we need to convert the period to seconds.
$$
begin{align*}
T = 5.7 cdot 60text{ s} = 342text{ s}
end{align*}
$$
Now we find the frequency directly from definition (1) as follows:
$$
begin{align*}
f = frac{1}{T} = frac{1}{342text{ s}} = 2.92 cdot 10^{-3} text{ Hz}
end{align*}
$$
For a mass $m$ attached to a spring with a spring constant $k$ we know that the period of simple harmonic oscillations will be:
$$
begin{equation}
T = 2 , pi ; sqrt{frac{m}{k}}
end{equation}
$$
When a spring is compressed or pulled by a given force $F$ its elongation $x$ is proportional to that force, and the coefficient is called the spring constant.
This is described by Hooke’s Law:
$$
begin{equation}
F = k , x
end{equation}
$$
begin{enumerate}[a)]
item
Looking carefully at the picture one can conclude that the period of the motion depends on the total effective spring constant of the system as described by formula (1). \
In the case of block 1 the springs are tied in parallel, so the total spring constant is double the normal value:
begin{align*}
k_1 = 2 cdot k
end{align*}
Looking at block 2 one can conclude that the springs act in union. If the block moves to the left, the left spring will be compressed and will push to the right, the right spring will be stretched and will pull to the right. Hence they act together.
\
The same result is found when analyzing the motion of the block to the right. So we conclude that the effective spring constant in the case of block 2 is the same as before:
begin{align*}
k_2 = 2 cdot k
end{align*}
Since we found the effective spring constants to be the same, $k_1 = k_2$, we conclude that the period will be the same as well.
item
The correct answer is B
end{enumerate}
item
The period of oscillations are the same
item
The correct answer is B
end{enumerate}
We know that the wavelength and frequency determine the speed of a wave. They are related by the following formula:
$$
begin{equation}
v = lambda cdot f
end{equation}
$$
We know that when a standing wave is formed in a string the number of antinodes determines the harmonic of the wave. This gives us a result that the length of the string is equal to a integer number of wavelength halves, that is:
$$
begin{align*}
L = frac{n cdot lambda}{2}
end{align*}
$$
Rearranging gives:
$$
begin{align*}
& 2 cdot L = n cdot lambda \
& lambda = frac{2L}{n}tag{ 2}
end{align*}
$$
From this we see that any wavelength lambda that fulfils this equation for an integer n can produce a standing wave.
Firstly we use the given speed $v = 402 ; frac{text{m}}{text{s}}$ and frequency $f = 603text{ Hz}$, to find the wavelength using formula (1) as follows:
$$
begin{align*}
& v = f cdot lambda \
& lambda = frac{v}{f} \
& lambda = frac{402 ; frac{text{m}}{text{s}}}{603text{ Hz} } approx 0.67text{ m}
end{align*}
$$
We have found the wavelength and since we know the length of the string to be equal $L = 1.33text{ m}$, we find the integer n that determines the number of antinodes of the standing wave using formula (2) as follows:
$$
begin{gather*}
lambda = frac{2L}{n} \
n = frac{2L}{lambda} \
n = frac{2 cdot 1.33text{ m}}{0.67text{ m}} approx 4
end{gather*}
$$
$$
begin{equation}
T = 2 , pi ; sqrt{frac{m}{k}}
end{equation}
$$
begin{enumerate}[a)]
item
The time that passes between two adjacent nodes is one half-period. From the figure we see that this time is $2text{ s}$. So we conclude the period is:
begin{align*}
T = 2 cdot 2text{ s} = 4text{ s}
end{align*}
item
The distance from the maximum elongation to the equilibrium position is the amplitude distance. From the figure we read this to be
begin{align*}
A = 0.5text{ m}
end{align*}
end{enumerate}
begin{enumerate}[c)]
item
We know the mass to be $m = 3.8text{ kg}$ and we have found the period to be $T = 4text{ s}$ in part a). \\
Now using formula 1 we can find the spring coefficient of stiffness $k$ as follows:
begin{align*}
T = 2 , pi ; sqrt{frac{m}{k}}
end{align*}
Rearranging for k we get
begin{align*}
& T^2 = 4 , pi^2 ; frac{m}{k} \
& k = frac{4 , pi^2 , m}{T^2}
end{align*}
Plugging in the numbers we get
begin{align*}
k = frac{4 , pi^2 cdot 3.8text{ kg}}{(4text{ s})^2} approx 9.37 ; frac{text{N}}{text{m}}
end{align*}
end{enumerate}
item
The period is $T = 4text{ s}$
item
The amplitude is $A = 0.5text{ m}$
item
The sprint constant is $k = 9.37 ; frac{text{N}}{text{m}} $
end{enumerate}
For a mass $m$ attached to a spring with a spring constant $k$ we know that the period of simple harmonic oscillations will be:
$$
begin{equation}
T = 2 , pi ; sqrt{frac{m}{k}}
end{equation}
$$
When a spring is compressed or pulled by a given force $F$ its elongation $x$ is proportional to that force, and the coefficient is called the spring constant.
This is described by Hooke’s Law:
$$
begin{equation}
F = k , x
end{equation}
$$
begin{enumerate}[a)]
item
A force of maximum magnitude is experienced when the body is in maximum elongation, that is, the body is in the amplitude of its motion. Looking at the figure we can see that the body is in amplitude at times $t = 1text{ s}, t = 3text{ s}, t = 5text{ s}$ , so these are the times when the force is maximum.
item
Similarly as we did in part a), know we will look at the moments in time when the body is in equilibrium, because that is when the force is minimum, that is zero. The moments are: $t =0text{ s}, t = 2text{ s}, t = 4text{ s}, t =6text{ s}$.
item
We know that the mass is $ m = 3.8text{ kg}$ , and from the figure we read the period to be $T = 4text{ s}$. Now using formula (1) we find the spring constant as follows:
begin{align*}
T = 2 , pi ; sqrt{frac{m}{k}}
end{align*}
Rearranging for $k$ we get:
begin{align*}
T^2 = 4 , pi^2 , frac{m}{k} \
k = frac{4 , pi^2 , m}{T^2}
end{align*}
Plugging in the numbers we get:
begin{align*}
k = frac{4 , pi^2 cdot 3.8text{ kg}}{ (4text{ s})^2} approx 9.37 ; frac{text{N}}{text{m}}
end{align*}
\
Now to find the magnitude of the maximum force the body experiences, we will find the force acting on it according to Hooke’s law, that us formula (2), in the amplitude position. From the graph we also read $A = 0.5text{ m}$. \
For more explanations on how $T$ and $A$ were found from the figure look at the solution of problem 108. \\
Finally we write:
begin{align*}
F = k cdot A
end{align*}
Plugging in the numbers we get:
begin{align*}
F = 9.37 ; frac{text{N}}{text{m}} cdot 0.5text{ m} approx 4.7text{ N}
end{align*}
end{enumerate}
item
The times when the force is maximum are: $t = 1text{ s}, t = 3text{ s}, t = 5text{ s}$
item
The times when the force is zero are: $t = 0text{ s}, t = 2text{ s}, t = 4text{ s}, t = 6text{ s}$
item
The magnitude of the maximum force is $F = 4.7text{ N}$
end{enumerate}
For a mass $m$ attached to a spring with a spring constant $k$ we know that the period of simple harmonic oscillations will be:
$$
begin{equation}
T = 2 , pi ; sqrt{frac{m}{k}}
end{equation}
$$
begin{enumerate}[a)]
item
We know the mass to be $m = 0.45text{ kg}$ and the period $T = 1.4text{ s}$ \
Now using formula 1 we can find the effective spring constant of the branch, as if it was a spring of coefficient of stiffness $k$, as follows:
begin{align*}
T = 2 , pi ; sqrt{frac{m}{k}}
end{align*}
Rearranging for $k$ we get
begin{align*}
& T^2 = 4 , pi^2 , frac{m}{k} \
& k = frac{4 , pi^2 , m}{T^2}
end{align*}
Plufginf in the numbers we get
begin{align*}
k = frac{4 , pi^2 cdot 0.45text{ kg}}{ (1.4text{ s})^2} approx 9.05 ; frac{text{N}}{text{m}}
end{align*}
item
When the crow flies away and the eagle lands, we have a new mass $m_2$ , but the spring constant of the branch remains the same as in part a. The new period is $T_2 = 3.6text{ s}$ , so again using formula (1), but this time solving for the mass we write
begin{align*}
T_2 = 2 , pi ; sqrt{frac{m_2}{k}}
end{align*}
Rearranging for the mass we get:
begin{align*}
& T_2^2 = 4 , pi^2 , frac{m_2}{k} \
& m_2 = frac{T_2^2 , k}{4 , pi^2}
end{align*}
Plugging in the numbers we have:
begin{align*}
m_2 = frac{(3.6text{ s})^2 cdot 9.05 ; frac{text{N}}{text{m}} }{4 , pi^2 } approx 3text{ kg}
end{align*}
end{enumerate}
item
The effective spring constant of the branch is $k = 9.05 ; frac{text{N}}{text{m}}$
item
The mass of the eagle is $m_2 = 3text{ kg}$
end{enumerate}
The period of a pendulum oscillating due to gravitational acceleration $g$ can be found using the length of the pendulum $L$ as follows:
$$
begin{equation}
T = 2 , pi sqrt{frac{L}{g}}
end{equation}
$$
begin{enumerate}[a)]
item
By looking at formula (1) we can see that the period $T$ of the pendulum is proportional to the square root of the length of the pendulum $L$, that is:
begin{align*}
T sim sqrt{L}
end{align*}
Next let us break up the total motion into two parts. One half period where the pendulum has length $L$, and the one half period where the pendulum has length $l$. Since:
begin{align*}
l < L text{ and } T sim sqrt{L}
end{align*}
we can conclude that the period of the pendulum with the peg is smaller than the period of the pendulum without the peg.
end{enumerate}
begin{enumerate}[b)]
item
As stated previously in part a the total period can be found as the sum of two half periods of the pendulums of length $L$ and $l$. Using formula (1) we can write:
begin{align*}
& T = frac{T_1}{2} + frac{T_2}{2} \
& T = frac{1}{2} left(2 , pi sqrt{frac{L}{g}} + 2 , pi sqrt{frac{l}{g}} right) \
& T = pi left(sqrt{frac{L}{g}} + sqrt{frac{l}{g}} right)
end{align*}
item
Now using $L = 1text{ m}$ and $l = 0.25text{ m}$ we can calculate the period:
begin{align*}
T = pi left(sqrt{frac{1text{ m}}{9.81 ; frac{text{m}}{text{s}^2}} } + sqrt{frac{0.25text{ m}}{9.81 ; frac{text{m}}{text{s}^2}}} right) approx 1.5text{ s}
end{align*}
end{enumerate}
item
The period of the pendulum with the peg is smaller than the period of the pendulum without the peg. \
item
$T = pi left(sqrt{frac{L}{g}} + sqrt{frac{l}{g}} right)$
item
T = 1.5text{ s}
end{enumerate}
Now, quartz timekeepers have become the world’s most widely used timekeeping technology. Even in computers and other appliances that keep time have quartz timekeeping.
The world’s first quartz clock was built by Warren Marrison and J. W. Horton in 1927 at Bell Telephone Laboratories. But world’s first quartz watch was made and developed by watchmaker Seiko. Which they unveiled in December 1969.
Quartz crystal is a specific form of a compound called silicon dioxide. It is also a piezoelectric material. That means when a quartz crystal is subject to mechanical stress, it accumulates electrical charge across some planes. In a reverse effect, if charges are placed across the crystal plane, quartz crystals will bend. Hence, quartz can be directly driven (to flex) by an electric signal.
The size of the quartz does not change much with temperature fluctuations. Therefore, its resonator does not change shape and a quartz clock will remain relatively accurate as the temperature changes. Hence, it is more accurate than pendulums and springs (which are affected by the temperature).
The usual quartz frequency is 32768 Hz, just high enough to exceed the human hearing range, yet low enough to permit inexpensive counters to derive a 1-second pulse.
Using some digital counter, driven by the frequency a digital pulse once per second is created. This pulse-per-second output can be used to drive many kinds of clocks.
In most clocks, the quartz resonator is in a small can or flat package of about 4 mm big.
We know that there exists a relation between the chirp rate of the snowy tree cricket and the temperature of its location. It follows the formula:
$$
begin{equation}
N = T -39
end{equation}
$$
Where $T$ is the temperature in Fahrenheit, and $N$ the number of chirps in $13text{ s}$.
Our cricket is observed to chirp 35 times in $13text{ s}$ so we know $N = 35$.
To find the temperature in Fahrenheit we simply apply formula (1) as follows:
$$
begin{align*}
N = T – 39
end{align*}
$$
Rearranging:
$$
begin{align*}
T = N + 39
end{align*}
$$
Plugging in the value for $N$ we get:
$$
begin{align*}
T = 35 + 39 = 74
end{align*}
$$
So finally
$$
begin{align*}
T = 74text{textdegree}text{F}
end{align*}
$$
The correct answer is C
We know that there exists a relation between the chirp rate of the snowy tree cricket and the temperature of its location. It follows the formula:
$$
begin{equation}
N = T -39
end{equation}
$$
Where $T$ is the temperature in Fahrenheit, and $N$ the number of chirps in $13text{ s}$.
We know the temperature in Fahrenheit $T = 68text{textdegree}text{F}$, so to find the chirp rate we simply apply formula (1) as follows:
$$
begin{align*}
N = T – 39
end{align*}
$$
Plugging in the value for $T$ we get:
$$
begin{align*}
N = 68 – 39 = 29
end{align*}
$$
We have found that the cricket chirps $N = 29$ times in $t = 13text{ s}$ so now we find the frequency by definition:
$$
begin{align*}
f = frac{N}{t} = frac{29}{13text{ s}} = 2.2text{ Hz}
end{align*}
$$
The correct answer is B

