
All Solutions
Page 944: Assessment
The mass number of carbon-13 is $A = 13$.
So the neutron number of carbon-13 is $N = A-Z = 13-6 = 7$.
carbon-13 has 7 neutrons.
Rubidium is the element with $Z=37$.
So the nucleus with 37 protons and 59 neutrons is $^{96}_{37}$Rb.
$$
begin{align*}
_{41}^{93} Nb = _{41}^{98} Nb < _{80}^{202} Hg < _{86}^{220} Rn
end{align*}
$$
begin{align*}
_{41}^{93} Nb = _{41}^{98} Nb < _{80}^{202} Hg < _{86}^{220} Rn
end{align*}
$$
We can calculate the neutron number for each isotope, such that:
$$
begin{align*}
_{41}^{93} Nb = 93 – 41 = 52 \
_{41}^{98} Nb = 98 – 41 = 57 \
_{80}^{202} Hg = 202 – 80 = 122 \
_{86}^{220} Rn = 220 – 86 = 134 \
end{align*}
$$
Considering the four isotopes that we have in the problem, we can rank them in order of increasing neutron number:
$$
begin{align*}
_{41}^{93} Nb < _{41}^{98} Nb < _{80}^{202} Hg < _{86}^{220} Rn
end{align*}
$$
begin{align*}
_{41}^{93} Nb < _{41}^{98} Nb < _{80}^{202} Hg < _{86}^{220} Rn
end{align*}
$$
$$
begin{align*}
_{41}^{93} Nb < _{41}^{98} Nb < _{80}^{202} Hg < _{86}^{220} Rn
end{align*}
$$
begin{align*}
_{41}^{93} Nb < _{41}^{98} Nb < _{80}^{202} Hg < _{86}^{220} Rn
end{align*}
$$
The mass number is conserved in a nuclear reaction.
On the left side of the reaction, the mass number is $235+1 = 236$.
On the right side the mass number is $132+101 = 233$.
Since mass number is conserved, there must be three neutrons released in the reaction.
$^1_0$n $+$ $^{235}_{92}$U $rightarrow$ $^{123}_{50}$Sn $+$ $^{101}_{42}$Mo $+$ 3$^1_0$n
On the left side the total atomic number is $1+1=2$.
Atomic number of neutron is zero.
So on the right side, the atomic number of missing nucleus must be 2.
Helium (He) is the element with atomic number 2.
The mass number on the left side of the reaction is $2+3 = 5$.
Mass number of neutron is 1. So the mass number of helium nucleus is $5-1 = 4$.
$^2_1$H $+$ $^3_1$H $rightarrow$ $^4_2$He $+$ $^1_0$n
The atomic number of the parent nucleus is $Z = 89$.
So the neutron number of the parent nucleus is $N = A-Z = 224 – 89 = 135$.
The parent nucleus undergoes alpha decay, that is, it emits two protons and two neutrons.
So the atomic number of the daughter nucleus is $Z = 89 – 2 = 87$.
The neutron number of the daughter nucleus is $N = 135 – 2 = 133$.
The mass number of the daughter nucleus is $A = 133 + 87 = 220$.
(b) $Z=87$
(c) $N = 133$
$dfrac{dE}{dt} = 3.90 times 10^{26}$ W
Find the rate that the Sun converts mass into energy ($dfrac{dm}{dt}$)
We first start with our mass-energy relationship: E = m$c^2$
From this equation, we can find the rates by getting the derivatives of E and m with respect to time, such that:$dfrac{dE}{dt} = dfrac{dm}{dt}c^2$
We can now calculate for the rate in kilograms per second:
$$
begin{align*}
dfrac{dm}{dt} &= dfrac{dE/dt}{c^2} \
&= dfrac{3.90 times 10^{26}W}{(3 times 10^{8} m/s)^2} \
&= boxed{4.33 times 10^{9} text{kg/s}}
end{align*}
$$
$Delta m = dfrac{dm}{dt} times time$
Since we know that the rate of conversion is in kg/s, we convert the time from years to seconds, such that:
time = $4.50 times 10^9 y = 1.42 times 10^{17} s$
We can now compute for $Delta m$:
$$
begin{align*}
Delta m &= (4.33 times 10^9 kg/s )times(1.42 times 10^{17} s) \
&= 6.15 times 10^{26} kg
end{align*}
$$
We can now obtain the percentage of mass converted to energy:
$$
begin{align*}
m_{percent} &= dfrac{Delta m}{m_{current}} times 100% \
&= dfrac{6.15 times 10^{26} kg}{2.00 times 10^{30} kg} times 100%\
&= boxed{0.0308 %}
end{align*}
$$
b) 0.0308 %
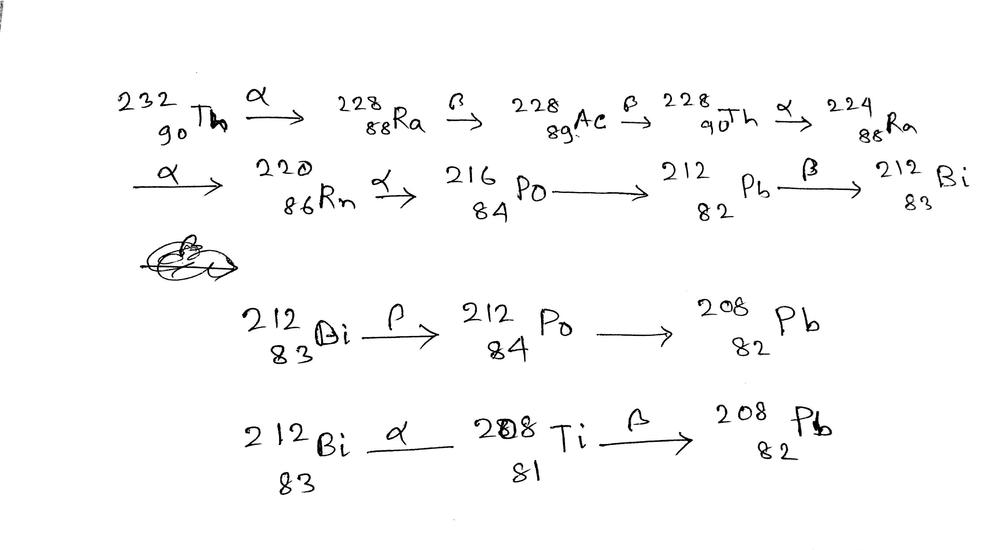
In gamma decay process, the excited nucleus comes to the ground state by emitting $gamma$-rays.
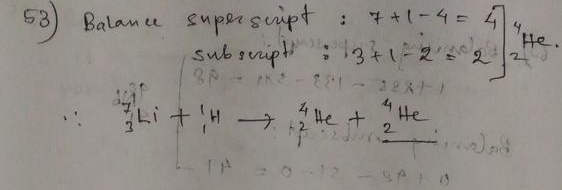
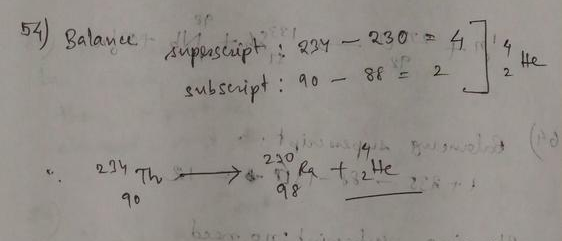
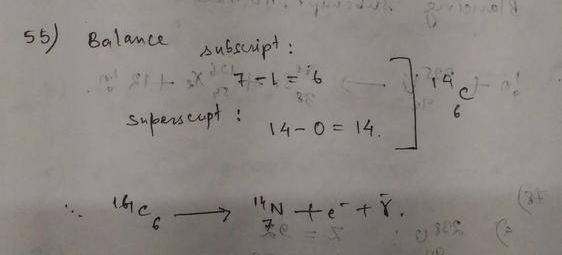
$$
begin{align*}
ce{^{238}_{92}U} rightarrow ce{^{234}_{90}Th}
end{align*}
$$
Here, we see that both the atomic number $Z$ and neutron number $N$ change by $2$. This is exactly the $alpha$ decay, a helium nucleus $ce{^{4}_{2}He}$ is ejected.
The second reaction is
$$
begin{align*}
ce{^{234}_{90}Th} rightarrow ce{^{234}_{91}Pa}
end{align*}
$$
Here, we see that the atomic number $Z$ changes by $1$ and the mass number $A$ stays the same. A neutron has been converted to a proton; we conclude that this step describes a $beta$ decay.
$$
begin{align*}
ce{^{234}_{91}Pa} rightarrow ce{^{234}_{92}U}
end{align*}
$$
Here, the atomic number $Z$ also changes by $1$ but the mass number $A$ stays the same. Same as in the step above, we conclude that this process is a $beta$ decay, because a neutron has been converted to a proton.
The finals step is
$$
begin{align*}
ce{^{234}_{92}U} rightarrow ce{^{230}_{90}Th}
end{align*}
$$
Here, both the atomic number $Z$ and the number of neutrons $N$ change by 2. We conclude that this step is an $alpha$ decay, because a helium nucleus $ce{^{4}_{2}He}$ has been ejected.
Finally, we write the types of decay in this decay chain as
$$
begin{align*}
boxed{alpha text{decay} rightarrow beta text{decay} rightarrow beta text{decay} rightarrow alpha text{decay}}
end{align*}
$$
alpha text{decay} rightarrow beta text{decay} rightarrow beta text{decay} rightarrow alpha text{decay}
$$
(a) For $^{212}_{84}$Po, $Z=84$ and $A = 212$. So the atomic number of the daughter nucleus is $Z = 84 – 2 = 82$. Lead is the element with atomic number 82.
The mass number of the lead nucleus is $A = 212 – 4 = 208$.
So the daughter nucleus is $^{208}_{82}$Pb.
The nuclear reaction is
$^{212}_{84}$Po $rightarrow$ $^{208}_{82}$Pb $+$ $^4_2$He $+$ energy.
(b) When $^{239}_{94}$Pu undergoes alpha decay, following the above arguments, the daughter nucleus has atomic number $Z=92$ and mass number $A=235$.
Uranium is the element with atomic number 92.
So the nuclear reaction is
$^{239}_{94}$Pu $rightarrow$ $^{235}_{92}$U $+$ $^4_2$He $+$ energy.
(a) The atomic number of $^{35}_{16}$S is 16. So when it undergoes beta decay, the daughter nucleus has the atomic number 17. Chlorine (Cl) is the element with atomic number 17. The mass number of chlorine is same as sulfur.
So the daughter nucleus is $^{35}_{17}$Cl.
The nuclear reaction is
$^{35}_{16}$S $rightarrow$ $^{35}_{17}$Cl $+$ e$^-$ $+$ $bar{gamma_e}$ $+$ energy.
Following the above arguments, the beta decay reaction of $^{212}_{82}$Pb can be written as
$^{212}_{82}$Pb $rightarrow$ $^{212}_{83}$Bi $+$ e$^-$ $+$ $bar{gamma_e}$ $+$ energy.
(a) When $^{18}_9$F undergoes $beta^+$ decay, the atomic number of the daughter nucleus is 10. Neon is the element with atomic number 10. The daughter nucleus is $^{18}_{10}$Ne. The nuclear reaction is
$^{18}_9$F $rightarrow$ $^{18}_{10}$Ne $+$ e$^+$ $+$ $gamma_e$ $+$ energy.
(b) Following the above arguments the $beta^+$ decay reaction of $^{22}_{11}$N can be written as
$^{22}_{11}$N $rightarrow$ $^{22}_{12}$Mg $+$ e$^+$ $+$ $gamma_e$ $+$ energy.
For $^{218}_{84}$Po, $Z=84$ and $A=218$.
(a) When it undergoes alpha decay, the atomic number of the daughter nucleus is $84 – 2 = 82$ and its mass number is $218 – 4 = 214$.
Lead is the element with atomic number 82. So the daughter nucleus is $^{214}_{82}$Pb.
The nuclear reaction is
$^{218}_{84}$Po $rightarrow$ $^{214}_{82}$Pb $+$ $^4_2$He $+$ energy.
(b) Energy released during alpha decay is 6.115 MeV.
$1:u = 931.5:MeV$
So change in mass is
$Delta m = 6.115:cancel{MeV} times dfrac{1:u}{931.5:cancel{MeV}} = dfrac{6.115}{931.5} :u = 0.006565:u$
$$
begin{align*}
ce{^{206}_{80}Hg} rightarrow ce{^{206}_{81}X} + e^- + bar{nu_e}
end{align*}
$$
where we’ve denoted the unknown element as $X$. We see that the atomic number $Z$ increased by $1$, resulting in an element with an atomic number of $81$; we conclude that the unknown element is thallium $Tl$.
b) We’re given that the released energy in the process $triangle E$ is
$$
begin{align*}
triangle E = 1.308 text{MeV}
end{align*}
$$
We calculate the change in mass that occurs in the process $triangle m$ as
$$
begin{align*}
boxed{triangle m}&=frac{triangle E}{c^2}\
&=boxed{1.308 frac{text{MeV}}{c^2}}
end{align*}
$$
b) $triangle m=1.308 frac{text{MeV}}{c^2}$
$$
begin{align*}
_{28}^{66}Ni rightarrow _{29}^{66}Cu + e^{-} + gamma_{e}^{-} + energy
end{align*}
$$
Hence, the daughter nucleus is $boxed{_{29}^{66}Cu}$
$$
begin{align*}
E &= (Delta m) times E_u \
E &= (0.0002705 text{u}) times (931.5 text{MeV}) \
E &= 0.252 text{MeV}
end{align*}
$$
Hence, the energy release is $boxed{text{0.252 MeV}}$
b) $0.0252$ MeV
nucleus is ${rm _{29}^{66}Cu}$.
The here we have $Delta m=0.0002705$, hence the energy released
is
$$
Delta E=left(0.0002705 {rm au}right)frac{931.5 {rm Mev}}{1 {rm au}}=0.2520 {rm MeV}
$$
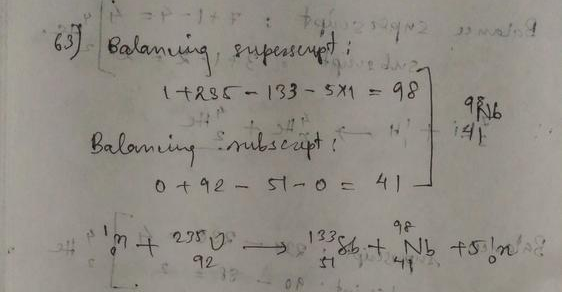
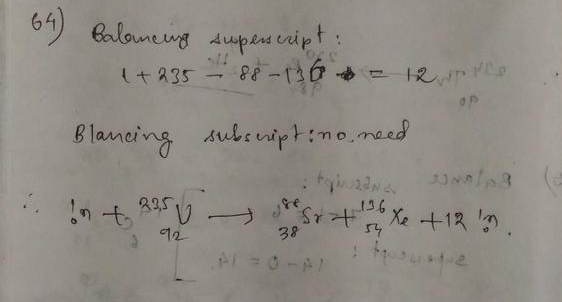
We know that, after a time interval of $t$, the number of samples that are still radioactive $N(t)$ is given by
$$
begin{align}
N(t)=N_0 left( frac{1}{2} right)^{frac{t}{t_frac{1}{2}}}
end{align}
$$
where $N_0$ is the number of radioactive samples at the beginning and $t_frac{1}{2}$ is the half-life of the material.
After $T=2 text{days}$ have passed, the number of samples that are still radioactive $N(t=T)$ is
$$
begin{align*}
N(t=T)=frac{N_0}{4}
end{align*}
$$
ie. only one-quarter of the sample is still radioactive.
By putting $t=T$ into Eq. (1), we get
$$
begin{align*}
N(t=T)=N_0 left( frac{1}{2} right)^{frac{T}{t_frac{1}{2}}}
end{align*}
$$
On the other hand, we know from the condition of the problem, that
$$
begin{align*}
N(t=T)&=frac{N_0}{4}\
&=N_0 left( frac{1}{2} right)^2
end{align*}
$$
By equating the last two expressions and cancelling out the number of radioactive samples at the beginning $N_0$, we get
$$
begin{align*}
left( frac{1}{2} right)^{frac{T}{t_frac{1}{2}}} = left( frac{1}{2} right)^2
end{align*}
$$
From here, we find the half-life of the material $t_frac{1}{2}$
$$
begin{align*}
boxed{t_frac{1}{2}}&=frac{T}{2}\
&=frac{2 text{days}}{2}\
&=boxed{1 text{day}}
end{align*}
$$
t_frac{1}{2}=1 text{day}
$$
We know that, after a time interval of $t$ has passed, the number of samples that are still radioactive $N(t)$ is given by
$$
begin{align}
N(t)=N_0 left( frac{1}{2} right)^{frac{t}{t_frac{1}{2}}}
end{align}
$$
where $N_0$ is the number of radioactive samples at the beginning, and $t_frac{1}{2}$ is the half-life of the material.
The half-life of the material $t_frac{1}{2}$ is
$$
begin{align*}
t_frac{1}{2}=122 text{s}
end{align*}
$$
We know from the condition of the problem that, after some (desired) time $T$, the number of samples that are still radioactive $N(t=T)$ is
$$
begin{align*}
N(t=T)&=frac{N_0}{128}\
&=N_0 left( frac{1}{2} right)^7
end{align*}
$$
On the other hand, the number of samples that are still active after a time interval of $T$ $N(t=T)$ is given by (we put $t=T$ into Eq. (1))
$$
begin{align*}
N(t)=N_0 left( frac{1}{2} right)^{frac{T}{t_frac{1}{2}}}
end{align*}
$$
By equating the last two expressions, we get
$$
begin{align*}
N_0 left( frac{1}{2} right)^7=N_0 left( frac{1}{2} right)^{frac{T}{t_frac{1}{2}}}
end{align*}
$$
From here, we can express the time interval $T$ and plug in the numerical value for the half-life of the material $t_frac{1}{2}$
$$
begin{align*}
boxed{T}&=7times t_frac{1}{2}\
&=7times 122 text{s}\
&=boxed{854 text{s}}
end{align*}
$$
T=854 text{s}
$$
$$
t=frac{5730text{ y}}{0.69}lnfrac{0.231}{0.121} =5370text{ y}.
$$
$$
t=frac{5730text{ y}}{0.69}lnfrac{R_{initial}}{0.0925 R_{initial}} = 19770text{ y}.
$$
$$
t=frac{5730text{ y}}{0.69}lnfrac{R_{initial}}{0.15 R_{initial}} = 15754text{ y}.
$$
a) $1/2=50%$ left;
b) $1/4 = 25%$ left;
c) $1/8 = 12.5%$ left.
Unlike leptons, hadrons are not elementary particles, meaning they do have internals structure. There are two types of hadrons: mesons and baryons. Mesons are made up of a quark and an antiquark. Baryons are made up of three quarks.
We conclude that the main difference between leptons and hadrons is that the leptons do not have internal structure and that the hadrons do.
Proton is hadron. It is made up of two up quarks and one down quark ($uud$). It is a baryon.
Muon is a lepton. It is an elementary particle.
Neutron is a hadron. Its internal structure is ($ddu$), that is, it is made up of two down quarks and one up quark. It is also a baryon.
Positron is a lepton. It is antiparticle of electron.
Hence, electron, muon, and positron are truly elementary particles.
Proton ($uud$) and neutron ($ddu$) are hadrons. They are made up of three quarks.
Short range forces – weak nuclear force and strong nuclear force
Weak nuclear force and strong nuclear force are short range forces. The range of strong nuclear force is $10^{-15}:m$ and of weak nuclear force is $10^{-18}:m$.
Electric charges of quarks are either $pmdfrac{2}{3}e$ or $pmdfrac{1}{3}e$.
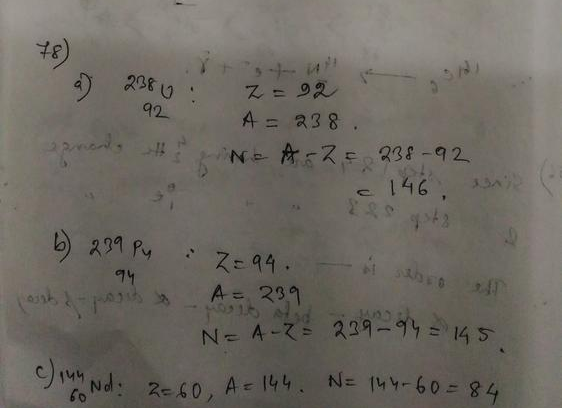
$$
begin{align*}
ce{^{3}_{1}H} rightarrow ce{^{3}_{2}He} + ? + ?
end{align*}
$$
We see that, before the reaction, the atomic number $Z_b$ is
$$
begin{align*}
Z_b=1
end{align*}
$$
After the reaction, the atomic number $Z_a$ is
$$
begin{align*}
Z_a=2
end{align*}
$$
We conclude that the atomic number increased by $1$, ie. a proton $p$ was created. On the other hand, the mass number $A$ stayed the same before and after the reaction $A=3$. Thus, we recognize this reaction as the $beta^-$ decay, written as
$$
begin{align*}
n rightarrow p + e^- + bar{nu_e}
end{align*}
$$
So, we conclude that the unknown particles are the electron $e^-$ and the electron antineutrino $bar{nu_e}$. Finally, we write the reaction as
$$
begin{align*}
boxed{ce{^{3}_{1}H} rightarrow ce{^{3}_{2}He} + e^- + bar{nu_e}}
end{align*}
$$
ce{^{3}_{1}H} rightarrow ce{^{3}_{2}He} + e^- + bar{nu_e}
$$
Also, because they have charges with opposite signes, they will be deflected in opposite directions.
by the amount of mass that is converted to energy during radioactive decay, which is much greater. Hence the amount of uranium required in nuclear power plant is much less compared to the amount of coal required in thermal power plant.
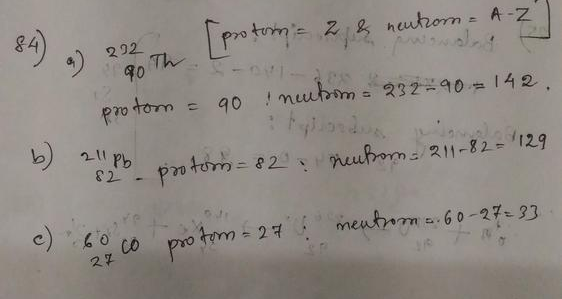
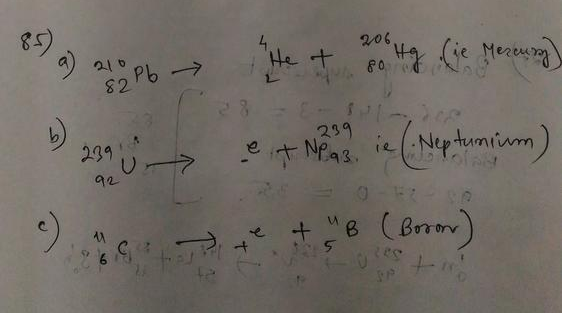
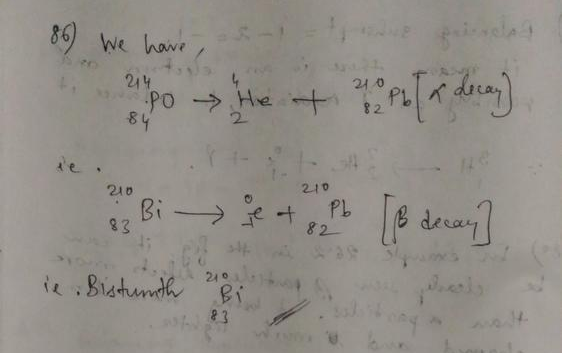
We know that, after a time interval $t$, the remaining mass of the radioactive material $m(t)$ is given by
$$
begin{align}
m(t)=m_0 left( frac{1}{2} right)^{frac{t}{t_frac{1}{2}}}
end{align}
$$
where $m_0$ is the mass of the material at the beginning and $t_frac{1}{2}$ is the half-life of the material.
The half life of the material $t_frac{1}{2}$ is
$$
begin{align*}
t_frac{1}{2}=1.405 times 10^{10} text{y}
end{align*}
$$
The mass of the material at the beginning $m_0$ is
$$
begin{align*}
m_0=328 text{mg}
end{align*}
$$
From the condition of the problem, we know that, after a time interval of $T$ (this is the desired time), we are left with the following mass of the material $m(t=T)$
$$
begin{align*}
m(t=T)=82 text{mg}
end{align*}
$$
On the other hand, using Eq. (1), $m(t=T)$ is given by
$$
begin{align*}
m(t=T)=m_0 left( frac{1}{2} right)^{frac{T}{t_frac{1}{2}}}
end{align*}
$$
By equating the last two expressions, we get
$$
begin{align*}
frac{82 text{mg}}{328 text{mg}}=left( frac{1}{2} right)^{frac{T}{t_frac{1}{2}}}
end{align*}
$$
or
$$
begin{align*}
left( frac{1}{2} right)^2=left( frac{1}{2} right)^{frac{T}{t_frac{1}{2}}}
end{align*}
$$
From the last equation, we calculate the required time $T$ as
$$
begin{align*}
boxed{T}&=2times t_frac{1}{2}\
&=2 times 1.405 times 10^{10} text{y}\
&=boxed{2.81times 10^{10} text{y}}
end{align*}
$$
T=2.81times 10^{10} text{y}
$$
b)Using the same logic as above we see than in one additional half-life half of the remaining $25%$ will decay leaving $12.5%$. In one more half-life there would only be $6.75%$ so the answer is 2 more half-lives i.e. $2.4times 10^{9}text{ y}.$
$$
t = frac{5730text{ y}}{0.69}lnfrac{7.82times0.231text{ Bq}}{1.38text{ Bq}} =2236text{ y}.
$$
b)Since $4$ half-lives of nucleus A have passed there remained $1/2^4 =1/16$ of the initial number of this type of nuclei. Since the starting number was $4$ times bigger than that of nuclei B we see that the mentioned $1/16$ is actually $1/4$ of the B type nuclei. This means than $2$ half lives of nuclei B have passed for two days i.e.
$$
T_{1/2}(B) = 1text{ d}.
$$
$$
E=Pt=120text{ W}times 2.5text{ d} = 2.592times 10^{7}text{ J} =1.62times10^{26}text{ eV}.
$$
This means than we need
$$
n=frac{E}{0.32times212text{ Mev} } = 2.38times 10^{18}text{ reactions}
$$
b) From the known value of released energy per one fission of Uranium we get the number of needed nuclei
$$
n’ = frac{E}{0.186E_u} =9.34times 10^{17}
$$
and that gives
$$
m_{Uranium} = n’times 235u = 3.64times{10^{-7}}text{ kg}
$$
$$
begin{align*}
boxed{ce{^{131}_{53}I}}
end{align*}
$$
$$
begin{gather*}
_{53}^{131} I rightarrow _{54}^{131} Xe + beta^-
end{gather*}
$$
Hence, the daughter nucleus is $boxed{_{54}^{131} Xe}$
$$
Delta m=(0.971 {rm Mev)frac{1 {rm u}}{931.6 {rm MeV}}=0.00104 {rm u}}
$$
So the correct answer is A.
After a time interval of $t$, the number of samples that are still radioactive $N(t)$ is given by
$$
begin{align}
N(t)=N_0 left( frac{1}{2} right)^{frac{t}{t_frac{1}{2}}}
end{align}
$$
where $N_0$ is the number of radioactive samples at the beginning and $t_frac{1}{2}$ is the half-life of the material.
The number of nuclei present at the beginning $N_0$ is
$$
begin{align*}
N_0=4times 10^{16}
end{align*}
$$
The half-life of the material $t_frac{1}{2}$ is
$$
begin{align*}
t_frac{1}{2}=8.03 text{d}
end{align*}
$$
From the condition of the problem, we know that, after some time $T$ (this is the required time interval), the number of nuclei that is still radioactive $N(t=T)$ is
$$
begin{align*}
N(t=T)=2.5times 10^{15}
end{align*}
$$
On the other hand, using Eq. (1), the number of remaining nuclei after a time $T$ $N(t=T)$ is given by
$$
begin{align*}
N(t=T)=N_0 left( frac{1}{2} right)^{frac{T}{t_frac{1}{2}}}
end{align*}
$$
By equating the last the expressions, we get
$$
begin{align*}
2.5times 10^{15}=N_0 left( frac{1}{2} right)^{frac{T}{t_frac{1}{2}}}
end{align*}
$$
We can now express the time $T$ and calculate it by plugging in the given numerical values
$$
begin{align*}
boxed{T}&=frac{t_frac{1}{2}ln{frac{N(t=T)}{N_0}}}{ln{frac{1}{2}}}\
&=frac{8.03 text{d} ln{frac{2.5times 10^{15}}{4times 10^{16}}}}{ln{frac{1}{2}}}\
&=boxed{32.1 text{d}}
end{align*}
$$

