
All Solutions
Page 909: Standardized Test Prep
$$
begin{align}
r_n=(5.3times 10^{-11}text{m})n^2
end{align}
$$
where $n$ is the principal quantum number.
For the first orbit $n=1$, we denote the radius as $r_1=R$
$$
begin{align*}
r_1=5.3times 10^{-11}text{m}=R
end{align*}
$$
For the third orbit $n=3$, the corresponding radius $r_3$ is given by
$$
begin{align*}
boxed{r_3}=(5.3times 10^{-11}text{m})3^2=boxed{9R}
end{align*}
$$
In other words, Bohr’s radius for the third orbit is nine times greater than Bohr’s orbit for the first orbit.
$$
begin{align*}
E_n=frac{k}{n^2}
end{align*}
$$
where $k$ is a constant. For the $n=1$ orbit, the energy of the electron $E_1$ is given by
$$
begin{align*}
E_1=E=frac{k}{1^2}=k
end{align*}
$$
Thus, we can write the energy of the electron in the $n$-th orbit $E_n$ as
$$
begin{align*}
boxed{E_n}=frac{k}{n^2}=boxed{frac{E}{n^2}}
end{align*}
$$
The frequency of the emitted light $nu$ when an electron jumps from an orbit $n_i$ to an orbit $n_f$ is given by
$$
begin{align}
nu=frac{-13.6text{eV}}{h} left( frac{1}{n_f^2}-frac{1}{n_i^2} right)
end{align}
$$
where $h=6.62times 10^{-34}text{Js}$ is Planck’s constant.
The inital orbit $n_i$ is
$$
begin{align*}
n_i=4
end{align*}
$$
The final orbit $n_f$ is
$$
begin{align*}
n_f=3
end{align*}
$$
In order to calculate the frequency of the photon $nu$, we just plug in the numerical values for the intial $n_i$ and final orbit $n_f$ into Eq. (1). But first, we will express the numerical value of Planck’s constant $h$ in the units of electron-volts using the relationship
$$
begin{align*}
1text{J}=6.24times 10^{18}text{eV}
end{align*}
$$
Finally, we calculate the frequency $nu$ as
$$
begin{align*}
boxed{nu}&=frac{-13.6text{eV}}{h} left( frac{1}{n_f^2}-frac{1}{n_i^2} right)\
&=frac{-13.6text{eV}}{6.62times 10^{34} times 6.24times 10^18 text{eV}} left( frac{1}{3^2}-frac{1}{4^2} right)\
&=boxed{1.6times 10^{14}text{Hz}}
end{align*}
$$
The wavelength of the emitted/absorbed photon $lambda$ occuring in a hydrogen atom electron transition is given by
$$
begin{align}
lambda=frac{hc}{triangle E}
end{align}
$$
where $h=41.31times 10^{-16}text{eV}$ is Planck’s constant, $c=3times 10^8frac{text{m}}{text{s}}$ is the speed of light in vacuum and $triangle E$ is the energy difference between two particular electron orbits.
A) From the given diagram, we read the energy difference $triangle E$ between the orbits $n=4$ and $n=2$
$$
begin{align*}
triangle E=2.55text{eV}
end{align*}
$$
From Eq. (1), we calculate the wavelength of the photon $lambda$
$$
begin{align*}
boxed{lambda}&=frac{hc}{triangle E}\
&=frac{41.31times 10^{-16}text{eV} times 3 times 10^8frac{text{m}}{text{s}}}{2.55text{eV}}\
&=boxed{486text{nm}}
end{align*}
$$
The wavelength correspoding to this electron transition belongs to the region of visible light.
B) From the given diagram, we read the energy difference $triangle E$ between the orbits $n=4$ and $n=1$
$$
begin{align*}
triangle E=12.75text{eV}
end{align*}
$$
From Eq. (1), we calculate the wavelength of the photon $lambda$
$$
begin{align*}
boxed{lambda}&=frac{hc}{triangle E}\
&=frac{41.31times 10^{-16}text{eV} times 3 times 10^8frac{text{m}}{text{s}}}{12.75text{eV}}\
&=boxed{97.2text{nm}}
end{align*}
$$
The wavelength correspoding to this electron transition does not belong to the region of visible light.
$$
begin{align*}
triangle E=12.09text{eV}
end{align*}
$$
From Eq. (1), we calculate the wavelength of the photon $lambda$
$$
begin{align*}
boxed{lambda}&=frac{hc}{triangle E}\
&=frac{41.31times 10^{-16}text{eV} times 3 times 10^8frac{text{m}}{text{s}}}{12.09text{eV}}\
&=boxed{102.5text{nm}}
end{align*}
$$
The wavelength correspoding to this electron transition does not belong to the region of visible light.
D) From the given diagram, we read the energy difference $triangle E$ between the orbits $n=3$ and $n=2$
$$
begin{align*}
triangle E=1.89text{eV}
end{align*}
$$
From Eq. (1), we calculate the wavelength of the photon $lambda$
$$
begin{align*}
boxed{lambda}&=frac{hc}{triangle E}\
&=frac{41.31times 10^{-16}text{eV} times 3 times 10^8frac{text{m}}{text{s}}}{1.89text{eV}}\
&=boxed{655.7text{nm}}
end{align*}
$$
The wavelength correspoding to this electron transition belongs to the region of visible light.
D) $n=2$ to $n=3$
$$
begin{align}
E=(-13.6text{eV}) left( frac{1}{n_f^2}-frac{1}{n_i^2} right)
end{align}
$$
In our case, $n_i$ is the ground state, ie.
$$
begin{align*}
n_i=1
end{align*}
$$
and $n_f$ is the principal quantum number that corresponds to the state of the electron when the atom is ionized, ie.
$$
begin{align*}
n_f rightarrow infty Rightarrow frac{1}{n_f} rightarrow 0
end{align*}
$$
Plugging these values into Eq. (1) gives us the amount of energy that an electron in the ground state of a hydrogen atom needs to absorbed in order to be ionized $E$
$$
begin{align*}
boxed{E}&=(-13.6text{eV}) left( frac{1}{n_f^2}-frac{1}{n_i^2} right)\
&=(-13.6text{eV}) (0-1)\
&=boxed{13.6text{eV}}
end{align*}
$$
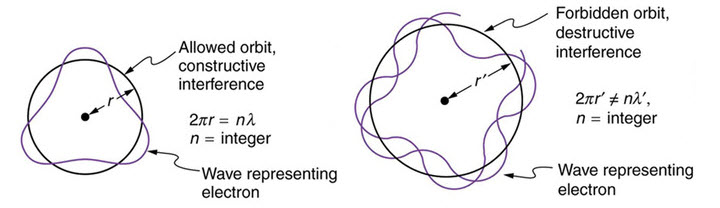
But $lambda = h/mv$ from de-Broglie formula. Hence $nh/mv=2pi r$.
Hence we get $L=mvr_n = nh/2pi$.
Haven't found what you were looking for?
Search for samples, answers to your questions and flashcards

