The magnetic field at a point produced by a current carrying wire is

$B = dfrac{mu_0 I}{2 pi r}$

where $I$ is the current flowing through the wire and $r$ is the radial distance of the point.

(a) Magnetic field is proportional to the current. So if the value of the current flowing through the wire is doubled, the magnetic field is doubled.

(b) Magnetic field is inversely proportional to the distance. So if the distance is doubled then the value of the magnetic field is halved.

Magnetic field produced by a loop carrying current $I$ is similar to that of a bar magnet. So a current carrying loop can be considered as a bar magnet.

When two loops with current flowing in the same direction are brought close to each other, this is same as opposite poles of two bar magnets approaching each other. So the force is attractive force.

When two loops carrying current in opposite directions are brought close to each other they repel each other. Because this is same bringing same poles of two bar magnets close to each other.

Magnetic field inside a solenoid of length $L$ with $N$ loops carrying current $I$ is given by

$B = mu_0 times (dfrac{N}{L}) times I$

Let the number of loops is halved and length of the solenoid is doubled then the new number of loops and new length are

$N’ = dfrac{N}{2}$ and $L’ = dfrac{L}{2}$

Magnetic field, $B’ = mu_0 times (dfrac{N’}{L’}) times I = mu_0 times dfrac{dfrac{N}{2}}{2L} times I = mu_0 times (dfrac{N}{4L}) times I = dfrac{B}{4}$

So the magnetic field decreases.

The magnetic field at a point produced by a long straight wire carrying the current $I$ is given by

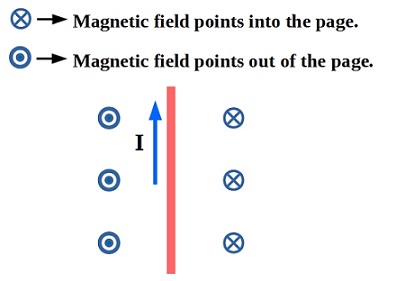
$B = dfrac{mu_0 I}{2 pi r}$

where $mu_0 = 4 pi times 10^{-7}:T.m.A^{-1}$ and $r$ is the radial distance of the point from the wire.

If the wire carries the current of $5.81:A$ then the magnetic field produced at radial distance of $6.25:cm = 0.0625:m$ is given by

$B = dfrac{^2 cancel{4pi} times 10^{-7} times 5.81}{cancel{2 pi} times 0.0625} = dfrac{2 times 5.81}{0.0625} times 10^{-7} = 186 times 10^{-7}:T$

$$
186 times 10^{-7}:T
$$

The magnetic field at a point produced by a long straight wire carrying a current $I$ is given by

$B = dfrac{mu_0 I}{2 pi r}$

where $mu_0 = 4 pi times 10^{-7}$ and $r$ is the radial distance of the point from the wire.

This relation can be rewritten for the radial distance at which the wire carrying $4.2:A$ current produces magnetic field of $1.3 times 10^{-5}:T$ as

$r = dfrac{mu_0 I}{2 pi B} = dfrac{^2 cancel{4pi} times 10^{-7} times 4.2}{cancel{2 pi} times 1.3 times 10^{-5}}=6.5 times 10^{-2}:m = 6.5:cm$

The magnetic field strength inside a solenoid is calculated using
$$
begin{aligned}
B = mu_0 left(frac{N}{L}right)I tag{1}
end{aligned}
$$
where $mu_0 = 4pi times 10^{-7};text{T}cdot text{m/A}$ is magnetic permeability of free space, $N$ is the number of turns of wire per meter, $L$ id the length of the solenoid and $I$ is the current through the wire.

**GIVEN**

Magnetic field: $B = 9.4times 10^{-5};text{T}$
Number of turns: $N = 250$ per meter
Length: $L = 0.12;text{m}$

We rearrange equation (1) such that $I$ is isolated on one side of the equation. And then we supply the known variables.
$$
begin{aligned}
I &= frac{BL}{mu_0 N} \ &= frac{(9.4times 10^{-5};text{T})(0.12;text{m})}{(4pi times 10^{-7};text{T}cdot text{m/A})left(250;frac{1}{text{m}}right)} \ &= 0.036;text{A} ;text{or } boxed{36;text{mA}}
end{aligned}
$$

$I = 36;text{mA}$

Current flowing in superconducting solenoid is, $I = 3.75:kA$.

Number of loops per meter of the solenoid is, $dfrac{N}{L} = 3250$.

The magnetic field produced inside the solenoid is

$B = mu_0 times (dfrac{N}{L}) times I$

where $mu_0 = 4 pi times 10^{-7}:T.m.A^{-1}$.

Substituting the values,

$B = 4 pi times 10^{-7} times 3250 times 3.75 times 10^3 =15.3:T$

$$
15.3:T
$$