The first two resistance are connected in series. So the resistance
of them is

$$
R_{1}=left(300 Omegaright)+(100 Omega)=400 Omega
$$

Now the third resistance is connected in parallel. Hence the equivalent
resistance is

$$
R_{eq}=frac{left(400 Omegaright)left(200 Omegaright)}{left(400 Omegaright)+left(200 Omegaright)}=133 Omega
$$

C is the correct answer.

The $100 Omega$ and $300 Omega$ resistance are in series, so
current flowing through them will be equal. And since the total resistance
of the series part is 400 $Omega$, which is greater than the other
resistance 200 $Omega$, the current through 200 $Omega$ is greater
than the other two. Hence the correct ranking is

$$
100 Omega=300 Omega<200 Omega
$$

C. $100 Omega=300 Omega<200 Omega$

The total power is given by

$$
P=frac{V^{2}}{R_{eq}}=frac{left(6 {rm V}right)^{2}}{133 Omega}=0.27 {rm W}
$$

If we replace the 200 $Omega$ resistance with 400 $Omega$ resistance,
then equivalent resistance becomes

$$
R_{eq}=frac{left(400 Omegaright)left(400 Omegaright)}{left(400 Omegaright)+left(400 Omegaright)}=200 Omega
$$

So the equivalent resistance will increase. Since the 300 $Omega$
and 100 $Omega$ resistance are in parallel with the 200 $Omega$.
The potential difference across them will not change. Hence the current
through 100 $Omega$ resistor will remain same and the potential
drop across the 300 $Omega$ resistance will remain same.

So B. and C. are correct.

The area of cross section of the first pencil is $A_{1}=frac{pi d^{2}}{4}=frac{pi(0.5)^{2}}{4} {rm mm^{2}}$.
If length of the pencil is $l$ and $rho$ is the resistivity then
the resistance is given by

$$
R=frac{rho l}{A_{1}}=frac{rho l}{pi(0.5)^{2}/4}
$$

When the diameter is $1.0$ mm, the area is $A_{2}=pi(1.0)^{2}/4 {rm mm^{2}}$.
The length is $l_{2}=l/2$. So the resistance is

$$
R_{2}=frac{rho l_{2}}{A_{2}}=frac{rho l/2}{pi(1.0)^{2}/4}
$$

Therefore we have

$$
frac{R}{R_{2}}=frac{frac{rho l}{pi(0.5)^{2}/4}}{frac{rho l/2}{pi(1.0)^{2}/4}}=left(frac{rho l}{pi(0.5)^{2}/4}right)left(frac{pi(1.0)^{2}/4}{rho l/2}right)=8
$$

so

$$
R_{2}=frac{R}{8}
$$

Answer A is correct answer.

Here we analyze the circuit below on the picture and would like to find out the magnitude and the direction of the current through the 300 $Omega$ resistor. The scheme of the circuit can be found below:

To calculate the current through the 300 $Omega$ resistor we need to find out the total current supplied from the battery, as all of it is passing through the 300 $Omega$ resistor and then separates on the two above resistors.

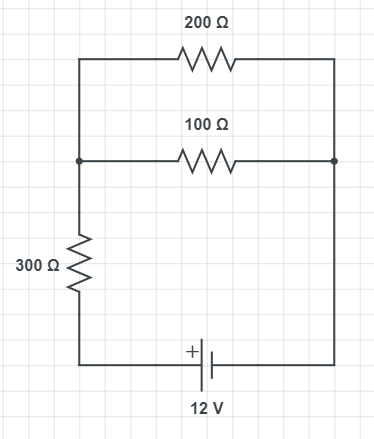
To calculate the equivalent resistance we need to first take into account two resistors that are in parallel and then serially add ti to the 300 $Omega$ resistor. For two resistors in series we have:

$$
frac{1}{R_{mathrm{eq}}}=frac{1}{R_{1}}+frac{1}{R_{2}}
$$

Putting in the numbers we have:

$$
frac{1}{R_{mathrm{eq}}}=frac{1}{100 mathrm{Omega}}+frac{1}{200 mathrm{Omega}} = 0.015 Omega
$$

We have the result:

$$
R_{mathrm{eq}} = 66.67 mathrm{Omega}
$$

Connecting it with our resistor in series we have:

$$
R_{tot} = 300 Omega + 66.67 Omega = 366.67 Omega
$$

Now to calculate the current we have:

$$
I=frac{V}{R_{tot}}
$$

Putting in the numbers we have:

$$
I = frac{12 mathrm{V}}{366.67 Omega}
$$

We get the result of:

$$
I = 0.33 mathrm{mA}
$$

Regarding the convention for the direction of the current, which is from positive to the negative terminal (we take into account that positive charges are current carriers, $textbf{due to the convention}$ and carefully looking at the schematics, we can see that direction of the current is upward through the 300 $Omega$ resistor.

$$
A. I = 0.18 mathrm{A}, text{upward}
$$

Since the 300 $Omega$ resistance is in series with other resistance,
the current flowing through 300 $Omega$ resistance will be equal
to the current flowing through the whole circuit. Hence the current
through 300 ohm resistance is greatest. Now since voltage across the
100 ohm and 200 ohm resistance are same. Hence current flowing through
100 ohm is greater than 200 ohm. So the rank accroding to current
flow will be

$$
300 Omega>100 Omega>200 Omega
$$