
All Solutions
Page 765: Lesson Check
$$
R_{mathrm{eq}}=R_{1}+R_{2}+R_{3}+R_{4} = 4R
$$
If we disconnect one, the total (equal) resistance will be only less then for one resistor and equal to the sum of those that are left:
$$
R_{mathrm{eq}}=R_{1}+R_{2}+R_{3}=3R
$$
R_{mathrm{eq}}=3R
$$
So when two of them connected parallel, the equivalent resistance will be
$$
R’=left[frac{1}{R}+frac{1}{R}right]^{-1}=frac{R}{2}
$$
When the third resistance will be connected in parallel with the above resistance then the equivalent resistance will be
$$
R”=left[frac{1}{R}+frac{1}{R}+frac{1}{R}right]^{-1}=frac{R}{3}
$$
Hence we have
$$
frac{R”}{R’}=frac{R/3}{R/2}=frac{2}{3}
$$
So final equivalent resistance will be $2/3$ of the initial equivalent resistance.
But in the parallel connection, all of the resistors are on the same wire that is connected to the source/power supply which makes sure, all of them are having the same potential difference, but the current is different.
Since they are connected in parallel even if one is not working, the other can work normally. We can also relate this we decorative light (e.g. for Christmas), they are all connected in parallel, so if few are not working, others can work normally. If they would be connected in series, breaking only one would mean stopping the work of all others, as well.
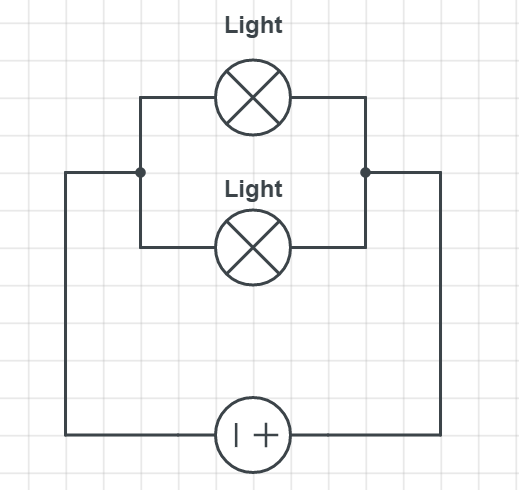
We need to calculate the emf of battery and we can do that using Ohm’s law:
$$
I=frac{varepsilon}{R_{mathrm{eq}}} Rightarrow varepsilon= IR_{eq}
$$
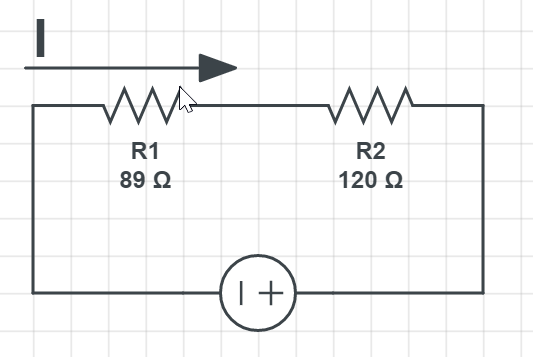
$$
R_{mathrm{eq}}=R_{1}+R_{2}
$$
Putting in the numbers we have:
$$
R_{mathrm{eq}}=89 Omega + 130 Omega
$$
which gives the result of:
$$
R_{mathrm{eq}}=219 Omega
$$
Now the emf of the battery is going to be:
$$
varepsilon=I R_{e q} = 0.72 mathrm{A} cdot 219 Omega
$$
which gives the result of:
$$
varepsilon=I R_{e q} = boxed{color{#c34632}157.68 mathrm{V}}
$$
varepsilon = 157.68 mathrm{V}
$$
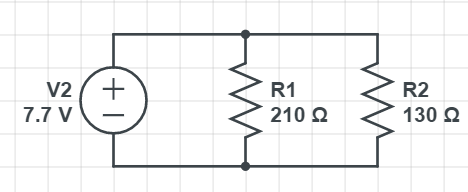
We know that when resistors are in parallel equal resistance is:
$$
frac{1}{R_{mathrm{eq}}}=frac{1}{R_{1}}+frac{1}{R_{2}}
$$
Putting in the numbers we have:
$$
frac{1}{R_{mathrm{eq}}}=frac{1}{210 Omega}+frac{1}{130 Omega} = frac{1}{0.01245}
$$
We have te result of:
$$
R_{mathrm{eq}} = 80.3 Omega
$$
From Ohm’s law we know:
$$
I=frac{V}{R_{text {eq }}} = frac{7.7 mathrm{V}}{80.3 Omega}
$$
We have the result of:
$$
boxed{color{#c34632}I=0.096 mathrm{A}}
$$
I=0.096 mathrm{A}
$$
For the $textbf{part a}$ we calculate the equivalent resistance, we can find out from Ohm’s law, diving voltage with current:
$$
R=frac{V}{I}
$$
putting in the numbers we have:
$$
R=frac{12 mathrm{V}}{0.25 mathrm{A}} = boxed{color{#c34632}48 mathrm{Omega}}
$$
Since the equal resistance is bigger the each of the specific resistors, we can conclude they are connected in $textbf{series}$, also they sum is giving exactly 48 $Omega$. Schematics of the circuit can be found in the Figure below:
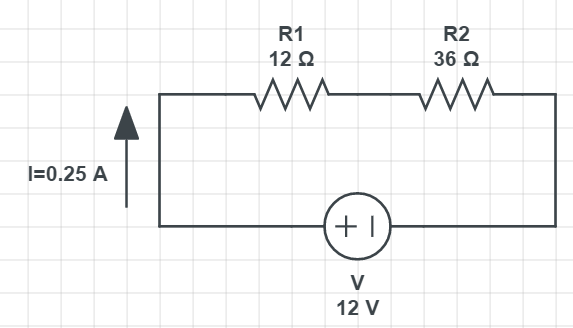
(a) 48 Omega
$$
$$
(b) mathrm{Series.}
$$
So, calling the upper resistors 1 and 2, we have equal resistance:
$$
R_{1,2} = R_1+ R_2
$$
Putting in the numbers we have:
$$
R_{1,2} = 35 Omega + 82 Omega = 117 Omega
$$
And know the total equal resistance will be:
$$
frac{1}{R_{mathrm{eq}}}=frac{1}{R_{1,2}}+frac{1}{R_{3}}
$$
Putting in the numbers:
$$
frac{1}{R_{mathrm{eq}}}=frac{1}{117 Omega}+frac{1}{45 Omega} = frac{1}{0.03077}
$$
we have the result:
$$
boxed{color{#c34632}R_{mathrm{eq}}=32.5 Omega}
$$
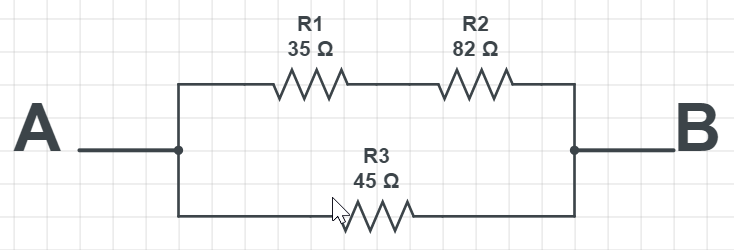
R_{mathrm{eq}}=32.5 Omega
$$
Haven't found what you were looking for?
Search for samples, answers to your questions and flashcards

