In this problem, we follow up on the $textbf{Example 21.7}$, where we solve the same circuit, but here instead of $450 mathrm{Omega}$, we have the $900 mathrm{Omega}$ resistor. For the $textbf{part a}$ we should determine is there any change in the current with the circuit. To determine what happens with the current, we look down to the circuit:

When all of the three resistors had totally equal resistance, the current was 0.040 A. Now since the resistance has increased of the upper resistor, it will allow less current to flow through. Also, since the current from the source gets in the junction before three resistors, it needs to $textbf{decrease}$.

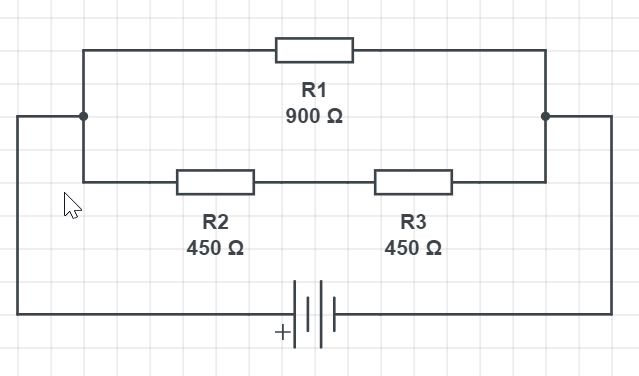
As the same amount of current is going through the lower two resistors and less through the upper one, we know that the total current is going to decrease.

To calculate the current we can follow the calculation from the Example:

$$
frac{1}{R_{mathrm{eq}}}=frac{1}{R_1}+frac{1}{2 R_{2,3}}
$$

Putting in the numbers we have:

$$
frac{1}{R_{mathrm{eq}}}=frac{1}{900 mathrm{Omega}}+frac{1}{2 cdot 450 mathrm{Omega}}
$$

which gives:

$$
frac{1}{R_{mathrm{eq}}}=frac{1}{0.002222 mathrm{Omega}}
$$

we have the result of:

$$
{R_{mathrm{eq}}}=450.45 mathrm{Omega}
$$

To get the current we have:

$$
I=frac{varepsilon}{R_{text {eq }}} = frac{12 mathrm{~V}}{450.45 Omega} = boxed{color{#c34632}0.027 mathrm{A}}
$$

$$
(a) mathrm{Decreases}
$$

$$
(b) I= 0.027 mathrm{A}
$$

Here we are to find the equivalent resistance between points A and B, as seen $mathrm{in}$ the picture below:

We have two resistor $R_1$, connected in series with resistors $R_2$ and $R_3$, but two of those are connected in parallel, so total (equal) resistance between points A and B would be:

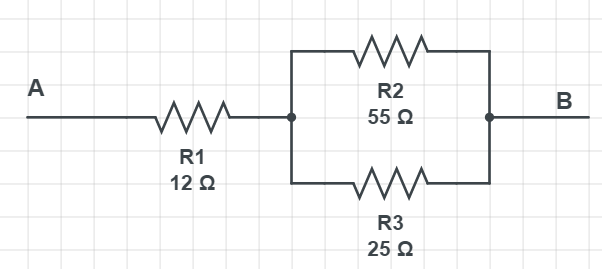
$$
R_{eq}=R_1 + R_{2,3}
$$

where $R_{2,3}$ is:

$$
frac{1}{R_{2,3}}= frac{1}{R_2} + frac{1}{R_3}
$$

putting in the numbers for $R_{2,3}$ gives:

$$
frac{1}{R_{2,3}}= frac{1}{55 mathrm{Omega}} + frac{1}{25 mathrm{Omega}}
$$

that gives:

$$
frac{1}{R_{2,3}}= 0.0581 mathrm{Omega} Rightarrow R_{2,3}= 17.19 mathrm{Omega}
$$

Now back to starting equation:

$$
R_{eq}=R_1 + R_{2,3} =12 mathrm{Omega} + 17.19 mathrm{Omega} = boxed{color{#c34632}29.19 mathrm{Omega}}
$$

$$
R_{eq} = 29.19 mathrm{Omega}
$$

In this problem, we analyze how to get a specific resistor from other resistors. We need a resistor of $150 Omega$ and we are to make it with a combination of $220 Omega$, $79 Omega$, and $92 Omega$.

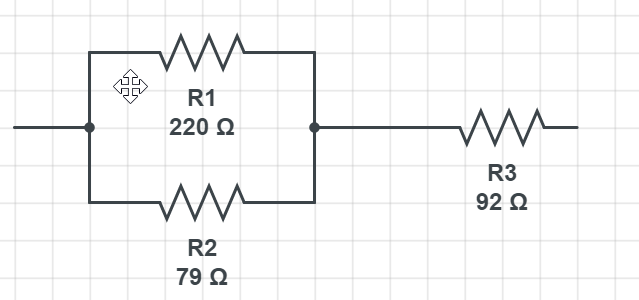
The first things to conclude is that we need to definitely connect $220 Omega$ in parallel with any of these, because connecting into the parallel will give $textbf{less resistance}$ then they are having together:

$$
frac{1}{R_{mathrm{eq}}}=frac{1}{R_{1}}+frac{1}{R_{2}}
$$

Putting in the numbers for first two resistors, we have:

$$
frac{1}{R_{mathrm{eq}}}=frac{1}{220 Omega}+frac{1}{79 Omega}= frac{1}{0.0172 Omega}
$$

where the result is:

$$
R_{eq} = 58.13 mathrm{Omega}
$$

Now getting back to start we can add the third one to this:

$$
R_{tot} = 58.13 mathrm{Omega} + 92 mathrm{Omega}
$$

which gives:

$$
R_{tot} = 150.13 mathrm{Omega}
$$

The correct scheme can be found in the picture below:

Connect $R_1$ and $R_2$ in parallel and $R_3$ in series with first two.