In this problem, we do the follow-up on Example 21.6.. The $R_3$ resistance is increased from 350 $Omega$ to the 525 $Omega$. We need to find the total resistance to find out if there is a change in current and we can do that usign the Ohm’s law.

Since the resistors are connected in parallel, the equal (total) resistance can be calculated as:

$$
frac{1}{R_{mathrm{eq}}}=frac{1}{R_{1}}+frac{1}{R_{2}}+frac{1}{R_{3}}
$$

Putting in the numbers we have:

$$
frac{1}{R_{mathrm{eq}}}=frac{1}{250 Omega}+frac{1}{150 Omega}+frac{1}{525 Omega}
$$

which gives the total resistance of:

$$
R_{mathrm{eq}}=frac{1}{0.01257 Omega^{-1}}=79.55 Omega
$$

now using Ohm’s law, we calculate the total current:

$$
I = frac{U}{R} = frac{24.0 mathrm{~V}}{79.55 Omega}
$$

which gives the result of:

$$
boxed{color{#c34632}I = 0.301 mathrm{A}}
$$

We can conclude from the numerical calculation that the current decreases, but even more from the formula for the total resistance in the parallel-connected resistors, we can see that raising the resistance by one resistor, will raise the total resistance in the circuit, which is going $textbf{lower}$ the current given by battery if we are looking the relation with the help of Ohm’s law.

$$
(a) Rightarrow mathrm{decreases}
$$

$$
(b) I= 0.301 mathrm{A}
$$

In this problem, we need to find what is the minimum number of 65 $mathrm{Omega}$ resistors to produce total resistance of 11 $mathrm{Omega}$ or less. To find the total of resistors resistance in a parallel circuit we do the following calculation:

$$
frac{1}{R_{e q}}=left(frac{1}{R_{1}}+frac{1}{R_{2}}+frac{1}{R_{3}}+ldots +frac{1}{R_{n}} right )
$$

We can call a minimum number of needed resistor for our problem n, so for equal resistance we have then:

$$
frac{1}{R_{e q}}=left(frac{n}{R}right)
$$

which gives for n:

$$
n=frac{R}{R_{e q}}
$$

Putting in the numbers we have:

$$
n=frac{65 Omega}{11 Omega}
$$

which gives the result of:

$$
n=5.9
$$

We can not possibly have 5.9 resistors, so this means we will need at least 6 resistors of 65 $mathrm{Omega}$ resistance to have wished eqaul resistance.

At least $mathrm{six}$ resistors.

In this problem, we analyze the circuits below, and the total current through the resistors is $1.8$ A.

Our goal is to find the emf of the battery, to find the emf we can use Ohm’s law:

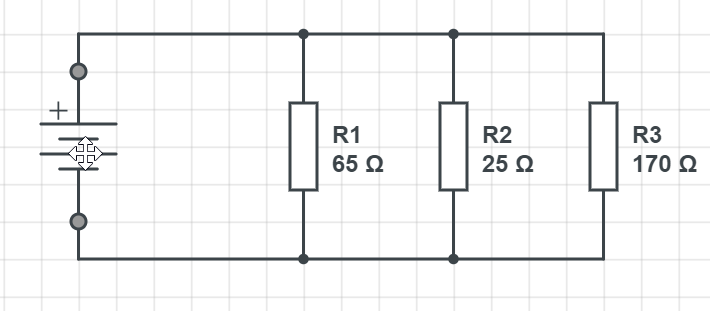
$$
I=frac{varepsilon}{R_{mathrm{eq}}}
$$

and we can see that knowing the current, first, we can calculate the equal resistance. Since we have a parallel connection use the following:

$$
frac{1}{R_{mathrm{eq}}}=frac{1}{R_{1}}+frac{1}{R_{2}}+frac{1}{R_{3}}
$$

putting in the numbers we have:

$$
frac{1}{R_{mathrm{eq}}}=frac{1}{65 Omega}+frac{1}{25 Omega}+frac{1}{170 Omega}
$$

which gives:

$$
R_{mathrm{eq}}=frac{1}{0.061267 Omega^{-1}}=16.32 Omega
$$

Now we calculate the emf with Ohm’s law:

$$
varepsilon=IR = 1.8 mathrm{A} cdot 16.32 Omega
$$

And we have the result of:

$$
boxed{color{#c34632}varepsilon= 29.37 mathrm{V}}
$$

$$
varepsilon= 29.37 mathrm{V}
$$