Here we are doing a follow up on Example 21.5. where the resistance of the third resistor was calculated and the potential difference across each. Instead of the problem statement from the Example, here all of the three resistors have equal value. To get the potential difference we use Ohm’s law:

$$
V=I R
$$

Since we know the current, which is 0.032 A, and the total resistance was 750 $Omega$, we know then that resistance on a single resistor is $frac{750 mathrm{Omega}}{3}$ which gives 250 $Omega$ on each resistor.

Since everything in this circuit is connected in series, the same amount of current is going trough each resistor, so the potential difference will be $textbf{equal}$ on each resistor:

$$
V= 250 Omega cdot 0.032 mathrm{~A}
$$

which gives the result of:

$$
V= 8 mathrm{~V}
$$

$$
V_{1=2=3}= 8 mathrm{~V}
$$

In this problem, we have the following circuit on the picture below, and it is said in the problem statement that the voltage difference on the $12-Omega$ resistor is 4.4 V.

For the $textbf{part a}$ we determine what is the potential difference on the $25 Omega$. Since all three resistors are connected in series we have the same amount of current going through all three resistors. Since we know the potential difference for the resistor 1, we can calculate the current going through it:

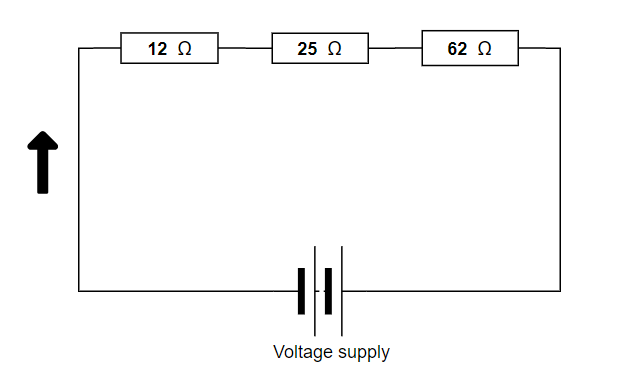
$$
I = frac{U}{R} = frac{4.4 mathrm{V}}{12 mathrm{Omega}} = 0.37 mathrm{A}
$$

Now we know the current through all three resistors, so we can calculate the potential difference for the second resistor:

$$
V = I cdot R_2
$$

which gives:

$$
V = 0.37 mathrm{A} cdot 25 mathrm{Omega} = boxed{color{#c34632}9.25 mathrm{V}}
$$

For the $textbf{part b}$ we need to calculate voltage difference on the third resistor, we do the same as in part a:

$$
V = I cdot R_3
$$

$$
V = 0.37 mathrm{A} cdot 62 mathrm{Omega} = boxed{color{#c34632}22.94 mathrm{V}}
$$

$$
(a) 9.25 mathrm{V}
$$

$$
(b) 22.94 mathrm{V}
$$

In this problem, we analyze the following circuit where we need to find the current going through it and potential difference across each resistor. To find a solution we know that resistor connected in series are having the same current going through each resistor, and also we will use Ohm’s law:

$$
R=frac{V}{I}
$$

To know the current we should calculate the total resistance in the circuit and then we will know how much current is given for a 12 V battery. To get the equal resistance we see they are connected in series, so the equal (total) resistance will be:

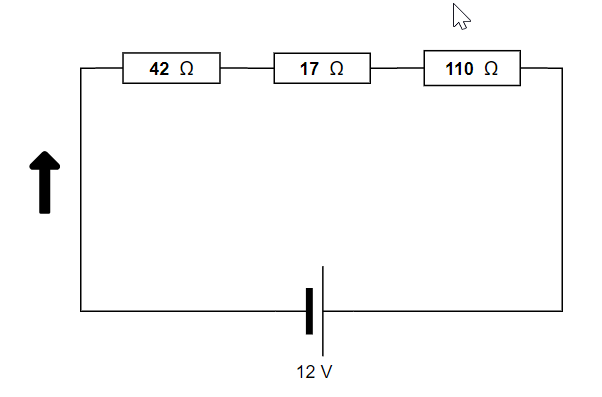
$$
R_{tot} = R_1 + R_2 + R_3
$$

which gives:

$$
R_{tot} = 42 mathrm{Omega} + 17 mathrm{Omega} + 110 mathrm{Omega}
$$

which gives:

$$
R_{tot} = 169 mathrm{Omega}
$$

Using Ohm’s law we calculate the current:

$$
I= frac{V}{R} = frac{12 mathrm{V}}{169 mathrm{Omega}} = boxed{color{#c34632}0.071 mathrm{A}}
$$

For the $textbf{part b}$ we calculate potential difference across each resistor, also using Ohm’s law:

$$
V_1 = I cdot R_1 = 0.071 mathrm{A} cdot 42 mathrm{Omega} = 2.98 mathrm{V}
$$

$$
V_2 = I cdot R_2 = 0.071 mathrm{A} cdot 17 mathrm{Omega} = 1.21 mathrm{V}
$$

$$
V_3 = I cdot R_3 = 0.071 mathrm{A} cdot 110 mathrm{Omega} = 7.81 mathrm{V}
$$

$$
(a) 0.071 mathrm{A}
$$

$$
(b) V_1=2.98 mathrm{V}, V_2=1.21 mathrm{V}, V_3=7.81 mathrm{V}
$$