Below is the attached picture. We should emphasize that direction of the electron is from the negative to the positive side of the battery, as electrons are negatively charged, this is different direction due to the $textbf{convention}$ of the current flow.

Also, we should comment that circuits like this can easily be shorted, as there is nothing that is consuming current in the circuit. But one should not forget that even the wire has the resistance which allows current normally to flow.

The sketched diagram $mathrm{in}$ the solution.

Here we analyze how does the current through a wire changes if the resistance is increased. Since we will be looking at the relationship between current and resistance, we assume that voltage for this circuit is $textbf{constant}$. First, we remember Ohm’s law:

$$
R=frac{V}{I}
$$

expressing the voltage from this we have:

$$
I=frac{V}{R}
$$

since the voltage is constant, from the relation we can see that current is inversely proportional to the resistance, which means that as much as I increase the resistance, for that much current will dropdown. This leads to the conclusion increasing the resistance in the circuit will lower the current.

Increasing the resistance $mathrm{lowers}$ the current.

The current in the wire will change if it is heated. Warmer the wire its resistance will increase. Since from Ohm’s law we know that current is inversely proportional to the resistance, the current will lower as we heat up the wire.

$$
R=frac{V}{I}
$$

If we have a wire at a temperature of 250 K and 300 K. Resistance at 300 K will be higher and current will be lower, rather than for the temperature of 250 K.

The reason this is happening can be also viewed in the origin of resistance in materials. Resistance is the intrinsic property and temperature is a measure of kinetic energy. So, higher the temperature, atoms inside the material move “more and faster” and due to all collisions and scatterings inside the material, we have a resistance as a result. This activity will be much higher as the temperature is higher.

If temperature $mathrm{is}$ increased, resistance will be higher.

Here we analyze how the flow of electrons is related to the areas of low and high potential. Since in the circuit, we have a battery that has a lower and higher end of potential. We know that electrons are negatively charged particles, so they will move in the direction from lower to the higher potential, in other words from negative to the positive area of potential ($textbf{positive terminal of the battery}$.

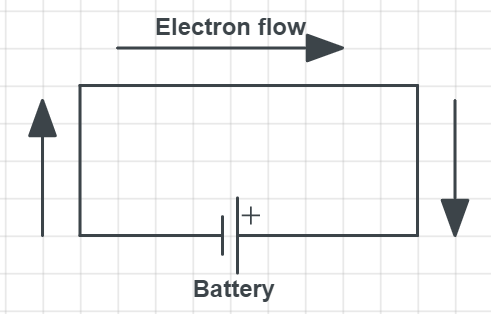
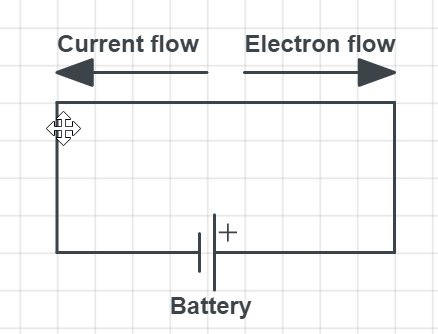
Contrary to this direction of the current is considered different by the convention, than the one explained above. For the current direction, we assume positive charges are moving. So, the real movement of electrons is considered opposite to the considered direction of the current movement.

Electrons move from the region $mathrm{of}$ lower potential to the higher value of potential.

Here we analyze the direction of the current if we know that current is produced by the electron that is falling toward the ground. The direction of the current will always be opposite to the direction of the electron, so the direction of the current will be $textbf{upward}$.

Direction $textbf{of}$ the current is upward.

If we would like to conduct a current through a diode we should connect a p-type semiconductor to the positive terminal of the battery. The reason for this is because the diode is technology based on semiconductors where the current carriers are not only electrons but holes, as well.

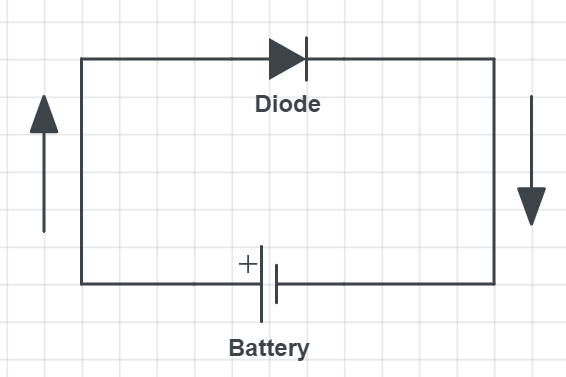
Because of specific $textbf{electronic structure}$ of semiconductors materials, we have a p-type and n-type of semiconductors where electrons or holes can be dominant charge carriers. For our case, if we connect p-type charge carriers can easily flow in the circuit and this is called $textbf{forward biased current}$.

We connect positive terminal $mathrm{to}$ the p-type semiconductor.

In this problem, we analyze two resistors, where their resistance and the current flowing through them is given. We determine their voltages. To determine their voltages, we simply use $textbf{Ohm’s law}$:

$$
R=frac{V}{I} Rightarrow V=IR
$$

From the problem statement, we know that $R_1= 10 mathrm{Omega}$ and $I_1 = 3 mathrm{~A}$, while $R_2= 5 mathrm{Omega}$ and $I_2 = 10 mathrm{~A}$.

Plugging in the numbers we have:

$$
V_1= I_1R_1 =3 mathrm{~A} cdot 10 mathrm{Omega}
$$

which gives:

$$
V_1= I_1R_1 =boxed{color{#c34632}30 mathrm{~V}}
$$

And for the second voltage we have:

$$
V_2= I_2R_2 =10 mathrm{~A} cdot 5 mathrm{Omega}
$$

we have the result of:

$$
V_2= I_1R_1 =boxed{color{#c34632}50 mathrm{~V}}
$$

We can conclude that resistor 2 has a greater potential difference.

Resistor 2 has a potential difference of $50$ V, which is greater than for resistor 1 that has a potential difference of 30 V.

In this problem, we use Ohm’s law to calculate a current through the resistor of resistance $220 mathrm{~Omega}$ and the voltage of 16 V. We use $textbf{Ohm’s law}$:

$$
I=frac{V}{R}
$$

Putting in the numbers we have:

$$
I=frac{16 mathrm{~V}}{220 mathrm{~Omega}}
$$

We get the result of:

$$
boxed{color{#c34632}I=0.073 mathrm{~A}}
$$

$$
I=0.073 mathrm{~A}
$$

We would like to produce 1.8 A current trough the 140$mathrm{~Omega}$ resistor, we need to find out what voltage we need to set up to produce this current. For this we use Ohm’s law:

$$
R=frac{V}{I} Rightarrow V=IR
$$

Putting in the numbers we have:

$$
V=1.8 mathrm{~A} cdot 140 mathrm{~Omega}
$$

We get the result of:

$$
boxed{color{#c34632}V= 252 mathrm{~V}}
$$

$$
V= 252 mathrm{~V}
$$

This problem is connected to Example 21.3 from the book and we look for how long does the flashlight need to work to produce 150 J of work. We can see that the emf delivered by the battery is 1.5 V and a current of 0.44 A is passing through the circuit.

Since we know the emf and the work needed to be done, we can calculate what amount of charge is being used in this circuit, with the relation for the work done by the battery.:

$$
W=(Delta Q) varepsilon
$$

expressing the charge from the relation above we have:

$$
Delta Q=frac{W} {varepsilon}=frac{150 mathrm{J}}{1.5 mathrm{~V}}
$$

which gives:

$$
Delta Q=100 mathrm{C}
$$

To get the time, we use the relation that defines the current:

$$
I=frac{Delta Q}{Delta t}
$$

Expressing time from this we have:

$$
Delta t=frac{Delta Q}{I} = frac{100 mathrm{C}}{0.44 mathrm{A}}
$$

which gives the result of:

$$
boxed{color{#c34632}Delta t=227.27 mathrm{~A}}
$$

$$
Delta t=227.27 mathrm{~A}
$$