Just as the mechanical work done when you lift a box onto a shelf is stored as gravitational potential energy, the mechanical work done on charges (an electrical system) is also stored in form of $electric;potential;energy$. Suppose you have a positive charge in one hand and a negative charge in the other. The charges attract one another, so as you pull your hands apart, you exert a force and do work (it’s like stretching a spring|you have to do work to increase the amount of stretch). This mechanical work is stored in the electric field as electric potential energy. If you release the charges, the speed up as they race toward each other, converting their electric potential energy into kinetic energy.

As a charge $q$ moves in the direction of the electric field, $vec{pmb E}$, the electric potential, $V$, decreases. In particular, if the charge moves a distance $d$, the electric potential decreases by the amount $Delta V = -Ed$.

Like many physical quantities, the electric potential obeys a simple $superposition$ principle. The total electric potential due to two or more charges is equal to the algebraic sum of the potentials due to the individual charges. By $algebraic;sum$ we mean that the potential of a given charge may be positive or negative. Thus, the algebraic sign of each potential must be taken into account when calculating the total potential. In particular, positive and negative contributions my cancel to give zero total potential at a given location.

$text{color{#4257b2}Picture the Problem}$

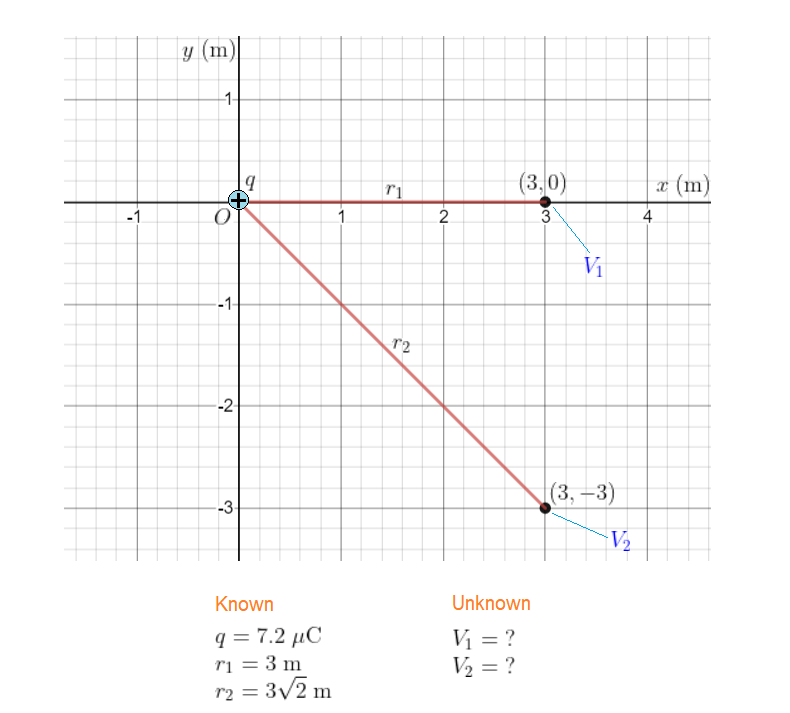
The situation is shown in our sketch, with the given charge and points of interest at their appropriate locations. The charge $q;(=7.2;mu$C) located at the origin is separated by a distance $r_1$ from the point (3.0,0) and a distance $r_2$ from the point $(3.0,-3.0)$. We call the electric potential due to $q$ at $r_1$ $V_1$ and at $r_2$ $V_2$.

$text{color{#4257b2}Strategy}$

The electric potential due to the charge $q$ can be found using $V = kq/r$, with $r = r_1$ for the location (3.0,0) and $r = r_2$ for the location $(3.0,-3.0)$.

$text{color{#4257b2}Solution}$

$textbf{(a)}$ Applying $V_1 = kq/r_1$, with $q = 7.2;mu$C and $r_1 = 3.0$ m, we find

$$
V_1 = (8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2)timesfrac{7.2times10^{-6};mathrm{C}}{3.0;mathrm{m}} = 2.2times10^4;mathrm{V}
$$

$textbf{(b)}$ Applying $V_2 = kq/r_2$, with $q = 7.2;mu$C and $r_2 = 3sqrt{2}$ m = 4.2 m, we find

$$
V_2 = (8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2)timesfrac{7.2times10^{-6};mathrm{C}}{4.2;mathrm{m}} = 1.5times10^4;mathrm{V}
$$

$textbf{(a)}$ $2.2times10^4$ V                         $textbf{(b)}$ $1.5times10^4$ V

$text{color{#4257b2}Picture the Problem}$

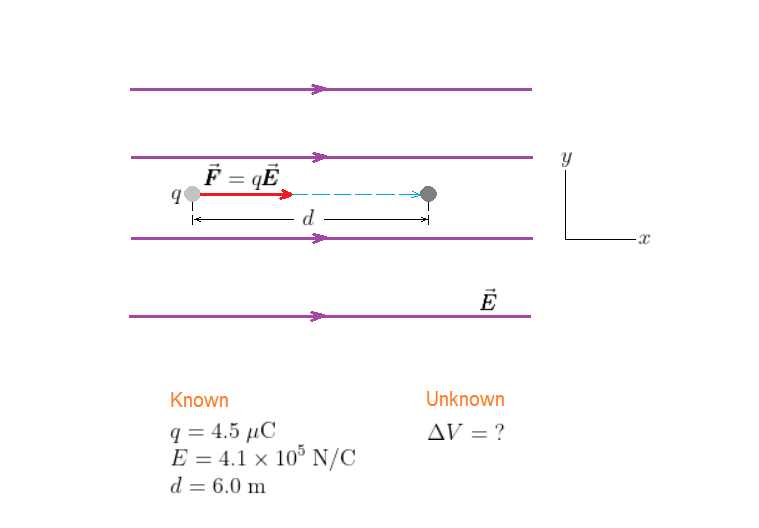
The situation is shown in our sketch. The 4.5-$mu$C charge, denoted by $q$, moves in a region of uniform electric field, which we call $vec{pmb E}$. The charge moves a distance $d = 6.0$ m in the positive $x$ direction.

$text{color{#4257b2}Strategy}$

As the charge $q$ moves in the direction of the electric field, $vec{pmb E}$, the electric potential, $V$, decreases. In particular, if the charge moves a distance $d$, the electric potential decreases by the amount $Delta V = -Ed$. Then the change in electric potential energy of $q$ is found using $Delta PE = qDelta V$.

$text{color{#4257b2}Solution}$

The change in electric potential is

$$
Delta V = -Ed = (4.1times10^5;mathrm{N/C})(6.0;mathrm{m}) = -2.5times10^6;mathrm{V}
$$

Hence, the change in electric potential energy of the charge $q$ is

$$
Delta PE = qDelta V = (4.5times10^{-6};mathrm{C})(-2.5times10^6;mathrm{V}) = -11;mathrm{J}
$$

$-11$ J

Known:

$E=100$ V/m

$dl=169$ m

Solution:

Potential difference $V$ is given by

$$
V=Edl=left(100 {rm V/m}right)left(169 {rm m}right)=1.69times10^{4} {rm V}
$$

$$
1.69times10^{4} {rm V}
$$

Known:

$$
q_{1}=+7.22 {rm mu C}=+7.22times10^{-6} {rm C}
$$

$$
q_{2}=-26.1 {rm mu C}=-26.1times10^{-6} {rm C}
$$

Electrostatic potential energy $U=-126$ J.

Solution:

The electrostatic potential energy is given by

$$
U=kfrac{q_{1}q_{2}}{r}
$$

or

$$
r=kfrac{q_{1}q_{2}}{U}=left(8.99times10^{9} {rm Nm^{2}/C^{2}}right)frac{left(+7.22times10^{-6} {rm C}right)left(-26.1times10^{-6} {rm C}right)}{left(-126 {rm J}right)}=1.34times10^{-2} {rm m}
$$