From Section 20.1, it is stated that the direction of an electric field is toward a negative charge and away from a positive charge. With this, the sign of the charge for an electric field that points away from it is $textbf{positive}$.

$textbf{(a)}$ Applying $E = k|q|/r^2$ with $q = 5.00;mu$C and $r = 1.00$ m yields

$$
begin{align*}
E &= kfrac{|q|}{r^2}\
&= (8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2)frac{5.00times10^{-6};mathrm{C}}{(1.00;mathrm{m})^2}\
&= 4.50times10^4;mathrm{N/C}
end{align*}
$$

$textbf{(b)}$ Applying $E = k|q|/r^2$ with $q = 5.00;mu$C and $r = 2.00$ m yields

$$
begin{align*}
E &= kfrac{|q|}{r^2}\
&= (8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2)frac{5.00times10^{-6};mathrm{C}}{(2.00;mathrm{m})^2}\
&= 1.12times10^4;mathrm{N/C}
end{align*}
$$

$textbf{(a)}$ $4.50times10^4;mathrm{N/C}$                $textbf{(b)}$ $1.12times10^4$ N/C

The expression for the magnitude $E$ of the electric field as a function of the distance $r$ is

$$
E = kfrac{|q|}{r^2}
$$

where $|q|$ is the magnitude of the charge producing the electric field. Solving for $r$ and substituting the known values, we find

$$
begin{align*}
r &= sqrt{frac{k|q|}{E}}\
&= sqrt{frac{(8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2)(11times10^{-6};mathrm{C})}{9.3times10^4;mathrm{N/C}}}\
&= 1.0;mathrm{m}
end{align*}
$$

$textbf{(a)}$ As we explained in Problem 11, the individual electric fields due to similar charges (have the same signs) at any point on the line connecting them point in opposite directions. Since the two charges have equal magnitudes, this means their electric fields at the midpoint will have the same magnitude, leading to zero total electric field. Since this is not the case (the total electric field at the midpoint has a nonzero value), we must have two charges with opposite signs. As shown in our sketch, the electric fields $E_1$ and $E_2$ due to the charges 1 and 2 (of equal magnitude $|q|$) at the midpoint of the line connecting them are in the same direction; in such case the total electric field has the nonzero magnitude of 45 N/C.

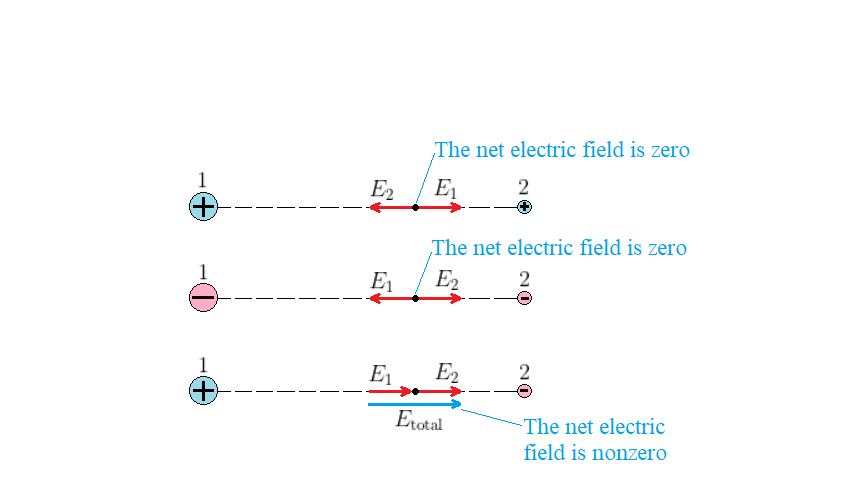
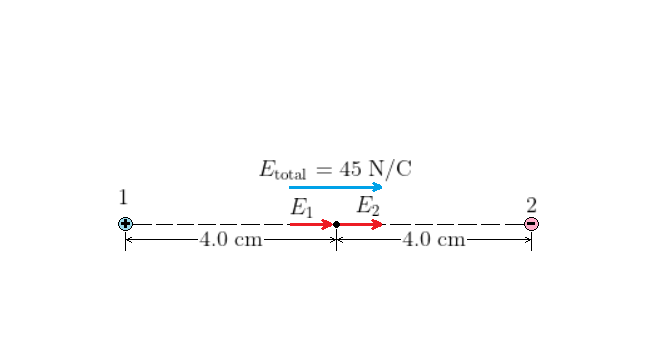
$textbf{(b)}$ The electric fields produced by the charges 1 and 2 at the midpoint on the line connecting them have the same magnitude $(E_1 = E_2)$, as the two charges have equal magnitudes and are the same distance from the midpoint (remember that $E = k|q|/d^2$). Because the total electric field is given by $E_{rm total} = E_1 + E_2$, we have

$$
E_1 = E_2 = frac{E_{rm total}}{2} = frac{45;mathrm{N/C}}{2} = 22.5;mathrm{N/C}
$$

Appling $E_1 = k|q|/d^2$, with $E_1 = 22.5$ N/C and $d = 4.0$ cm (see the sketch below) and solving for $|q|$, we find

$$
begin{align*}
|q| &= frac{E_1d^2}{k}\
&= frac{(22.5;mathrm{N/C})(4.0times10^{-2};mathrm{m})^2}{8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2}\
&= 4.00;mathrm{pC}
end{align*}
$$

$textbf{(a)}$ opposite

$textbf{(b)}$ 4.00 pC