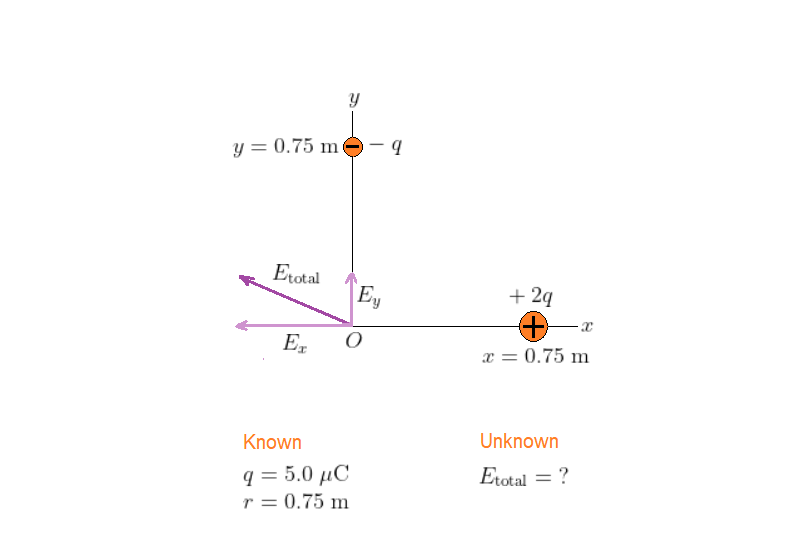
The situation, as we see in our sketch, is basically the same as Example 20.4, with the only difference that the $x$ component of the electric field now is two times larger and points in the opposite direction. This is an expected result, as we changed the sign of the charge on the $x$ axis and doubled its magnitude (remember that the magnitude of the electric field is directly proportional to the magnitude of the charge producing it). So, the calculations are basically the same except that we now replace $E_x$ by $2E_x$, which, of course, changes the magnitude of the total electric field.

$text{color{#4257b2}Solution}$

The $y$ component of the electric field remains unchanged: $E_y = 8.0times10^4$ N/C. Because $E = kq/r^2$ and $q$, on the $x$ axis, doubles in magnitude, we obtain

$$
E_x = 2times(8.0times10^4;mathrm{N/C}) = 1.6times10^5;mathrm{N/C}
$$

Hence, the total electric field is

$$
begin{align*}
E_{rm total} &= sqrt{E_x^2 + E_y^2}\
&= sqrt{(8.0times10^4;mathrm{N/C})^2 + (1.6times10^5;mathrm{N/C})^2}\
&= 1.8times10^5;mathrm{N/C}
end{align*}
$$