
All Solutions
Page 71: Standardized Test Prep
$$
begin{align*}
Delta x&=x_{f}-x_{i}\
&=15 text{m}-0\
&=quadboxed{15 text{m}}\
end{align*}
$$
Therefore, the correct answer is $textbf{(C)}$.
textbf{(C)}
$$
$$
begin{align*}
y=ax+b\
end{align*}
$$
where $a$ is the slope and $b$ is the intercept.
We can also describe motion with the slope-intercept form of the line equation
$$
begin{align*}
x_{f}=x_{i}+vt\
end{align*}
$$
with $x_{i}$ being the intercept and $v$ the slope.
If the velocity of an object is constant in time, then the slope of the line will be constant as well. Therefore, we can conclude that the correct answer is $textbf{(B)}$.
textbf{(B)}
$$
$$
begin{align*}
Delta x&=x_{f}-x_{i}\
&=20 text{m}-0\
&=quadboxed{20 text{m}}\
end{align*}
$$
Therefore, the correct answer is $textbf{(D)}$.
$$
begin{align*}
v_{avg}&=dfrac{Delta x}{Delta t}=dfrac{x_{f}-x_{i}}{t_{f}-t_{i}}\
&=dfrac{20 text{m}-25 text{m}}{10 text{s}-8 text{s}}\
&=dfrac{-5 text{m}}{2 text{s}}\
&=quadboxed{-2.5 frac{text{m}}{text{s}}}\
end{align*}
$$
Therefore, the correct answer is $textbf{(B)}$.
For the first part, we have:
$$
begin{align*}
v_{avg,1}&=dfrac{Delta x_{1}}{Delta t_{1}}=dfrac{x_{f,1}-x_{i,1}}{t_{f,1}-t_{i,1}}\
&=dfrac{30 text{m}-0}{6 text{s}-0}\
&=quadboxed{5 frac{text{m}}{text{s}}}\
\
abs{v_{avg,1}}&=abs{5 frac{text{m}}{text{s}}}\
&=quadboxed{5 frac{text{m}}{text{s}}}\
end{align*}
$$
and for the second part
$$
begin{align*}
v_{avg,2}&=dfrac{Delta x_{2}}{Delta t_{2}}=dfrac{x_{f,2}-x_{i,2}}{t_{f,2}-t_{i,2}}\
&=dfrac{20 text{m}-30 text{m}}{10 text{s}-6 text{s}}\
&=dfrac{-10 text{m}}{4 text{s}}\
&=quadboxed{-2.5 frac{text{m}}{text{s}}}\
\
abs{v_{avg,2}}&=abs{-2.5 frac{text{m}}{text{s}}}\
&=quadboxed{2.5 frac{text{m}}{text{s}}}\
end{align*}
$$
The equation of motion for runner A is
$$
begin{align*}
x_{A}=left(3.0 frac{text{m}}{text{s}}right)times t\
end{align*}
$$
and the equation of motion for runner B is
$$
begin{align*}
x_{B}=20 text{m}-left(2.0 frac{text{m}}{text{s}}right)times t\
end{align*}
$$
When they meet, their positions are the same, so we are solving the equation $x_{A}=x_{B}$ for $t$:
$$
begin{align*}
left(3.0 frac{text{m}}{text{s}}right)times t&=20 text{m}-left(2.0 frac{text{m}}{text{s}}right)times t\
left(3.0 frac{text{m}}{text{s}}+2.0 frac{text{m}}{text{s}}right)times t&=20 text{m}\
rightarrowquad t&=dfrac{20 text{m}}{5.0 frac{text{m}}{text{s}}}\
&=quadboxed{4.0 text{s}}\
end{align*}
$$
To find out their position, we just have to substitute $t$ with $4.0 text{s}$ in either equation.
$$
begin{align*}
x&=3.0 frac{text{m}}{text{s}}cdot 4.0 text{s}\
&=quadboxed{12 text{m}}\
end{align*}
$$
Therefore, the correct answer is $textbf{(D)}$.
Option $textbf{(A)}$ is an example of instantaneous velocity.
Option $textbf{(B)}$ is a bit deceitful; the speed of an object is constant, but when moving in a circle, the direction constantly changes; therefore, this isn’t the right answer either.
More or less the same applies for $textbf{(C)}$, speed could be constant during the entire drive, but the direction changes.
This leaves us with $textbf{(D)}$, the speed is constant and the direction of motion remains unchanged, which means that the velocity is also constant.
$$
begin{align*}
y=b+ax quadLongrightarrowquad x=12text{m}+left(5 frac{text{m}}{text{s}}right)times t\
end{align*}
$$
We can immediately eliminate $textbf{(A)}$ because this option implies that there was a change in velocity; the slope of a straight line is constant which means that velocity is constant, too.
Option $textbf{(B)}$ is obviously not true, as well as option $textbf{(D)}$; acceleration implies a change in velocity.
This leaves us with $textbf{(C)}$: the object moves with a constant velocity of $5 frac{text{m}}{text{s}}$.
$$
begin{align*}
v_{1}&=dfrac{d_{1}}{t_{1}}\
rightarrowquad d_{1}&=v_{1}t_{1}\
&=2 frac{text{m}}{text{s}}times 30 text{min}cdotdfrac{60 text{s}}{1 text{min}}\
&= quadboxed{3600 text{m}}
end{align*}
$$
and when walking west
$$
begin{align*}
v_{2}&=dfrac{d_{2}}{t_{2}}\
rightarrowquad d_{2}&=v_{2}t_{2}\
&=1 frac{text{m}}{text{s}}times 1 text{h}cdotdfrac{3600 text{s}}{1 text{h}}\
&= quadboxed{3600 text{m}}
end{align*}
$$
The total distance is the sum of these two distances
$$
begin{align*}
d&=d_{1}+d_{2}\
&=3600 text{m}+3600 text{m}\
&=quadboxed{7200 text{m}}\
end{align*}
$$
We know that displacement is the net change in position; i.e., the difference between final and initial position. In this case, we’ll have to calculate the hiker’s displacement as we would calculate the hypotenuse of a right-angled triangle with equal catheti.
Having all this in mind, the displacement is
$$
begin{align*}
(Delta x)^{2}&=(3600 text{m})^{2}+(3600 text{m})^{2}\
&=25 920 000 text{m}^{2}\
\
rightarrowquadDelta x&=sqrt{25 920 000 text{m}^{2}}\
&=5091.168825 text{m}\
&=quadboxed{5091 text{m}}\
end{align*}
$$
When writing the final result, we used $textbf{the rules for mathematical operations for significant figures.}$
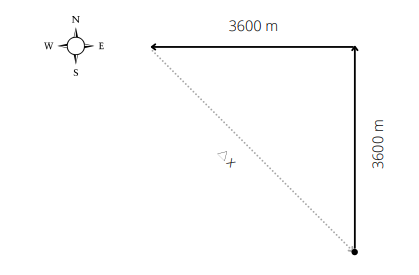
$textbf{Distance is a scalar,}$ which means that it has no direction associated with it, it is just a number representing the total length covered during motion, and it’s defined as always being positive.
$textbf{Displacement, however, is a vector,}$ meaning that it has both magnitude and direction. It’s defined as the net change in position, so, relative to the chosen origin and positive direction , it can be positive, negative, or zero.
It’s also important to know that displacement of an object can never be greater than the distance it covered.
begin{align*}
textbf{(a)} quad &boxed{d=7200 text{m}}\
\
textbf{(b)} quad &boxed{Delta x=5091 text{m}}\
\
textbf{(c)} quad &text{Distance is a scalar, whereas displacement is a vector.}\
end{align*}
$$
Haven't found what you were looking for?
Search for samples, answers to your questions and flashcards

