
All Solutions
Page 694: Lesson Check
$Q = sigma A = sigma times 4 pi R^2$
where $A=4 pi R^2$ is the surface area of the sphere.
Now the total on the sphere of radius $dfrac{R}{2}$ with same surface charge density $sigma$ is given by
$Q’ = sigma times 4 pi times (dfrac{R}{2})^2 = dfrac{sigma times 4 pi R^2}{4} = dfrac{Q}{4}$
Thus the charge on the sphere with radius $dfrac{R}{2}$ is quarter of the charge on the sphere of radius $R$.
Since electric force is proportional to the charge, the force exerted by the sphere of radius $dfrac{R}{2}$ on a point charge is less than the force exerted by the original sphere.
{color{#4257b2}text{Picture the Problem}}
$$
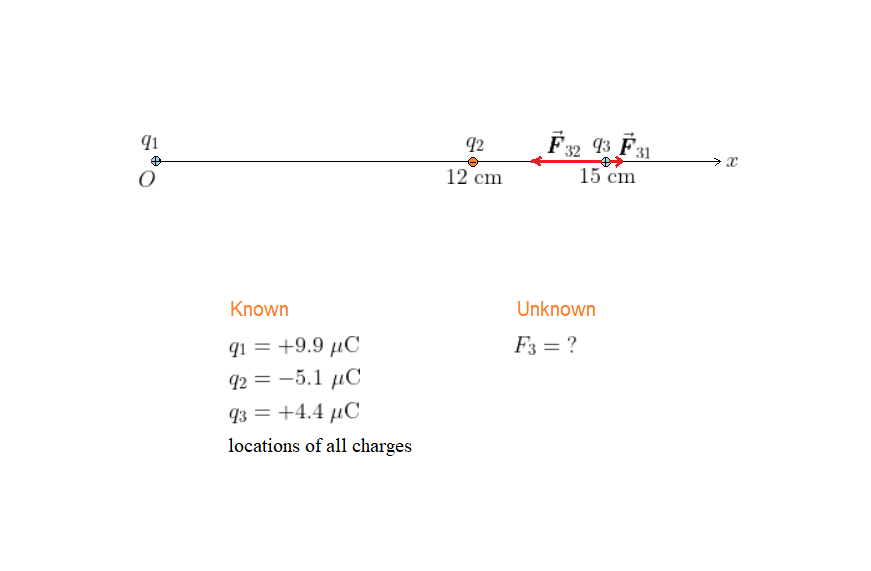
The situation is shown in our sketch, with each charge at its appropriate location. Notice that the forces exerted on charge $q_3$ by the charges $q_1$ and $q_2$ are in opposite directions. We give the force on $q_3$ due to $q_1$ the label $vec{pmb F}_{31}$ and the force on $q_3$ due to $q_2$ the label $vec{pmb F}_{32}$.
$$
{color{#4257b2}text{Strategy}}
$$
The total force on $q_3$ is the vector sum of the forces due to $q_1$ and $q_2$. In particular, notice that $vec{pmb F}_{31}$ points in the positive $x$ direction and $vec{pmb F}_{32}$ points in the negative $x$ direction. The magnitude of $vec{pmb F}_{31}$ is $k|q_1||q_3|/r^2$, with $r = 15$ cm. Similarly, the magnitude of $vec{pmb F}_{32}$ is $k|q_2||q_3|/r^2$, with $r = 3.0$ cm.
$$
{color{#4257b2}text{Solution}}
$$
$$
begin{align*}
vec{pmb F}_{31} &= +kfrac{|q_1||q_3|}{r^2}\
&= +(8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2)timesfrac{(9.9times10^{-6};mathrm{C})(4.4times10^{-6};mathrm{C})}{(15times10^{-2};mathrm{m})^2}\
&= +17;mathrm{N}qquad(text{positive};x;text{direction})\
vec{pmb F}_{32} &= -kfrac{|q_2||q_3|}{r^2}\
&= -(8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2)timesfrac{(5.1times10^{-6};mathrm{C})(4.4times10^{-6};mathrm{C})}{(3.0times10^{-2};mathrm{m})^2}\
&= -224;mathrm{N}qquad(text{negative};x;text{direction})\
vec{pmb F}_3 &= vec{pmb F}_{31} + vec{pmb F}_{32}\
&= 17;mathrm{N} – 224;mathrm{N}\
&= -207;mathrm{N}qquad(text{negative};x;text{direction})
end{align*}
$$
$$
{color{#4257b2}text{Insight}}
$$
The total force acting on $q_3$ has the magnitude of 207 N, and it points in the negative $x$ direction. Notice that the force due to $q_2$ is greater than that due to $q_1$, even though $q_1$ has the greater magnitude. The reason is that $q_2$ is five times closer to $q_3$ than $q_1$ is.
{color{#4257b2}text{Picture the Problem}}
$$
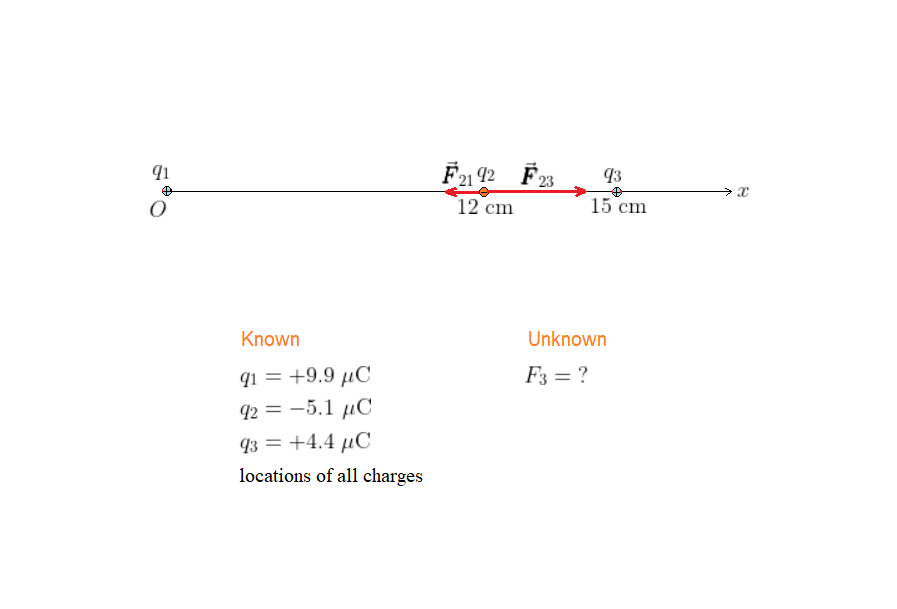
The situation is shown in our sketch, with each charge at its appropriate location. Notice that the forces exerted on charge $q_2$ by the charges $q_1$ and $q_3$ are in opposite directions. We give the force on $q_2$ due to $q_1$ the label $vec{pmb F}_{21}$ and the force on $q_2$ due to $q_3$ the label $vec{pmb F}_{23}$.
$$
{color{#4257b2}text{Strategy}}
$$
The total force on $q_2$ is the vector sum of the forces due to $q_1$ and $q_3$. In particular, notice that $vec{pmb F}_{21}$ points in the negative $x$ direction and $vec{pmb F}_{23}$ points in the positive $x$ direction. The magnitude of $vec{pmb F}_{21}$ is $k|q_1||q_2|/r^2$, with $r = 12$ cm. Similarly, the magnitude of $vec{pmb F}_{23}$ is $k|q_2||q_3|/r^2$, with $r = 3.0$ cm.
$$
{color{#4257b2}text{Solution}}
$$
$$
begin{align*}
vec{pmb F}_{21} &= -kfrac{|q_1||q_2|}{r^2}\
&= -(8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2)timesfrac{(9.9times10^{-6};mathrm{C})(5.1times10^{-6};mathrm{C})}{(12times10^{-2} ;mathrm{m})^2}\
&= -32;mathrm{N}qquad(text{negative};x;text{direction})\
vec{pmb F}_{23} &= kfrac{|q_2||q_3|}{r^2}\
&= (8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2)timesfrac{(5.1times10^{-6};mathrm{C})(4.4times10^{-6};mathrm{C})}{(3.0times10^{-2};mathrm{m})^2}\
&= 224;mathrm{N}qquad(text{positive};x;text{direction})\
vec{pmb F}_2 &= vec{pmb F}_{21} + vec{pmb F}_{23}\
&= -32;mathrm{N} + 224;mathrm{N}\
&= 192;mathrm{N}qquad(text{positive};x;text{direction})
end{align*}
$$
$$
{color{#4257b2}text{Insight}}
$$
The total force acting on $q_2$ has the magnitude of 192 N, and it points in the positive $x$ direction. Notice that the force due to $q_3$ is greater than that due to $q_1$, even though $q_1$ has the greater magnitude. The reason is that the charge $q_3$ is four times closer to $q_2$ than $q_1$ is.
where $sigma$ is the surface charge density and $A$ is the surface area of the sphere.
Substituting the values of $sigma$ and $A$,
$Q = +12.1:dfrac{mu C}{cancel{m^2}} times 0.0224:cancel{m^2} = +0.271:mu C$.
For a point charge outside the sphere, it is like a charge $Q=+0.271:mu C$ concentrated at the center of the sphere.
From Coulomb’s law, the square of the separation ($r$) between a point charge ($q=+1.75:mu C$) and center is the sphere can be written as
$r^2 = k dfrac{|Q| |q|}{F}$
where $k = 8.99 times 10^{9}:N.m^2/C^2$ and $F$ is the magnitude of the force between the sphere and point charge.
Substituting the value of $F$ and charges,
$r^2 = dfrac{8.99 times 10^9 times 0.271 times 10^{-6} times 1.75 times 10^{-6}}{46.9 times 10^{-3}}$
$r^2 = dfrac{8.99 times 0.271 times 1.75}{46.9} times 10^9 times 10^{-6} times 10^{-6} times 10^3 = 0.091:m^2$
So, $r = sqrt{0.091} :m = 30.2:cm$
Separation between the point charge and the center of the sphere is $30.2:cm$
30.2:cm
$$
{color{#4257b2}text{Picture the Problem}}
$$
The situation is shown in our sketch, with the charge $q_3$ at the unknown coordinate $x_0$. Notice that the forces exerted on charge $q_3$ by the charges $q_1$ and $q_2$ are in opposite directions. We give the force on $q_3$ due to $q_1$ the label $vec{pmb F}_{31}$ and the force on $q_3$ due to $q_2$ the label $vec{pmb F}_{32}$.
$$
{color{#4257b2}text{Strategy}}
$$
The total force on $q_3$ is the vector sum of the forces due to $q_1$ and $q_2$. In particular, notice that $vec{pmb F}_{31}$ points in the negative $x$ direction and $vec{pmb F}_{32}$ points in the positive $x$ direction. Suppose the total force acting on $q_3$ is zero at the location $x_0$, then we require $vec{pmb F}_{31} + vec{pmb F}_{32} = 0$. The magnitude of $vec{pmb F}_{31}$ is $k|q_1||q_3|/r^2$, with $r = x_0$. Similarly, the magnitude of $vec{pmb F}_{32}$ is $k|q_2||q_3|/r^2$, with $r = (1.00;mathrm{m} – x_0)$. We add the two forces (each with the appropriate sign) and solve for $x_0$.
$$
{color{#4257b2}text{Solution}}
$$
$$
begin{align*}
vec{pmb F}_{31} + vec{pmb F}_{32} &= 0\
-kfrac{|q_1||q_3|}{x_0^2} + kfrac{|q_2||q_3|}{(1.00;mathrm{m} – x_0)^2} &= 0\
-frac{|q_1|}{x_0^2} + frac{|q_2|}{(1.00;mathrm{m} – x_0)^2} &= 0\
-|q_1|[x_0^2 – (2.00;mathrm{m})x_0 + 1.00;mathrm{m}^2] + |q_2|x_0^2 &= 0\
(|q_2| – |q_1|)x_0^2 + (2.00;mathrm{m})|q_1|x_0 – (1.00;mathrm{m}^2)|q_1| &= 0\
(2.2;mumathrm{C} – 5.4;mumathrm{C})x_0^2 + (2.00;mathrm{m})(5.4;mumathrm{C})x_0&\ – (1.00;mathrm{m}^2)(5.4;mumathrm{C}) &= 0\
3.2x_0^2 – (10.8;mathrm{m})x_0 + 5.4;mathrm{m}^2 &= 0
end{align*}
$$
This is a quadratic equation in $x_0$, with solutions $x_0 = 2.76$ m and $x_0 = 0.61$ m. Since we know $0<x_0<1.00$ m, the accepted solution must be $x_0 = 0.61$ m.
$$
{color{#4257b2}text{Insight}}
$$
The equilibrium point is closer to the charge $q_2$ because the charge $q_1$ has the greater magnitude.

Haven't found what you were looking for?
Search for samples, answers to your questions and flashcards

