$$
{color{#4257b2}text{Picture the Problem}}
$$

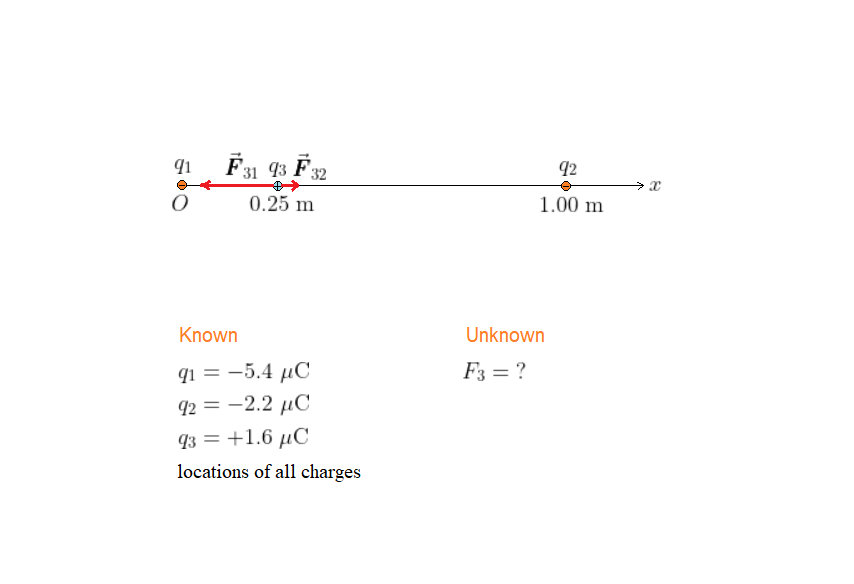
The situation is shown in our sketch, with each charge at its appropriate location. Notice that the forces exerted on charge $q_3$ by the charges $q_1$ and $q_2$ are in opposite directions. We give the force on $q_3$ due to $q_1$ the label $vec{pmb F}_{31}$ and the force on $q_3$ due to $q_2$ the label $vec{pmb F}_{32}$.

$$
{color{#4257b2}text{Strategy}}
$$

The total force on $q_3$ is the vector sum of the forces due to $q_1$ and $q_2$. In particular, notice that $vec{pmb F}_{31}$ points in the negative $x$ direction and $vec{pmb F}_{32}$ points in the positive $x$ direction. The magnitude of $vec{pmb F}_{31}$ is $k|q_1||q_3|/r^2$, with $r = 0.25$ m. Similarly, the magnitude of $vec{pmb F}_{32}$ is $k|q_2||q_3|/r^2$, with $r = 0.75$ m.

$$
{color{#4257b2}text{Solution}}
$$

$$
begin{align*}
vec{pmb F}_{31} &= -kfrac{|q_1||q_3|}{r^2}\
&= -(8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2)timesfrac{(5.4times10^{-6};mathrm{C})(1.6times10^{-6};mathrm{C})}{(0.25;mathrm{m})^2}\
&= -1.2;mathrm{N}qquad(text{negative};x;text{direction})\
vec{pmb F}_{32} &= kfrac{|q_2||q_3|}{r^2}\
&= (8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2)timesfrac{(2.2times10^{-6};mathrm{C})(1.6times10^{-6};mathrm{C})}{(0.75;mathrm{m})^2}\
&= 0.056;mathrm{N}qquad(text{positive};x;text{direction})\
vec{pmb F}_3 &= vec{pmb F}_{31} + vec{pmb F}_{32}\
&= -1.2;mathrm{N} + 0.056;mathrm{N}\
&= -1.1;mathrm{N}qquad(text{negative};x;text{direction})
end{align*}
$$

$$
{color{#4257b2}text{Insight}}
$$

The total force acting on $q_3$ has the magnitude of 1.1 N, and it points in the negative $x$ direction. Notice that the force due to $q_1$ is much greater than that due to $q_2$. The reason is that the charge $q_1$ has a magnitude that is about 2.5 times that of $q_2$ and it is also three times closer to $q_3$ than $q_2$ is.

1.1 N in the negative $x$ direction

The total electrostatic force on $q_1$ is the vector sum of the electric forces due to $q_2$ and $q_3$. In particular, notice that $vec{pmb F}_{12}$, the force exerted on $q_1$ due to $q_2$, points to the right and $vec{pmb F}_{13}$, the force exerted on $q_1$ due to $q_3$, points to the left. The magnitude of $vec{pmb F}_{12}$ is $k|q_1||q_3|/r^2$, with $r = d$. Similarly, the magnitude of $vec{pmb F}_{13}$ is $k|q_1||q_3|/r^2$, with $r = 2d$. Assuming the positive direction points to the right, the total force is

$$
begin{align*}
vec{pmb F}_1 &= vec{pmb F}_{12} + vec{pmb F}_{13}\
&= +kfrac{q(2.0q)}{d^2} – kfrac{q(3.0q)}{(2d)^2}\
&= left(2 – frac{3}{4}right)kfrac{q^2}{d^2}\
&= frac{5}{4}left(8.99times10^9;mathrm{N}cdotmathrm{m}^2/mathrm{C}^2right)timesfrac{(12times10^{-6};mathrm{C})^2}{(16times10^{-2};mathrm{m})^2}\
&= 63;mathrm{N}qquad(text{to the right})
end{align*}
$$

(a) Let the charge $q_1 = +12:mu C$ is at the origin ($x=0$). Then the charge $q_2 = -2.0 times 12 = -24:mu C$ is at $x =16:cm = 0.16:m$ and the charge $q_3 = 3.0 times 12:mu C = 36: mu C$ is at $x=32:cm = 0.32:m$.

So the separation of charge $q_2$ from $q_1$ and $q_3$ is $d=0.16:m$.

The magnitude of the force on $q_2$ due to $q_1$ is

$F_{21} = k dfrac{|q_1| |q_2|}{d^2}$ where $k = 8.99 times 10^9:N.m^2/C^2$.

So, $F_{21} = dfrac{8.99 times 10^9 times 12 times 10^{-6} times 24 times 10^{-6}}{0.16^2}$

$F_{21} = dfrac{8.99 times 12 times 24}{0.16^2} times 10^9 times 10^{-6} times 10^{-6} = 101.14:N$

Since both charges are of opposite kind, this force is an attractive force and points in the negative $x$-direction. That is,

$vec{F}_{21} = – 101.14 hat{x}$

The magnitude of force on $q_2$ due to $q_3$ is

$F_{23} = k dfrac{|q_2| |q_3|}{d^2}$

So, $F_{23} = dfrac{8.99 times 10^9 times 24 times 10^{-6} times 36 times 10^{-6}}{0.16^2}$

$F_{23} = dfrac{8.99 times 24 times 36}{0.16^2} times 10^9 times 10^{-6} times 10^{-6} = 303.42hat{x}:N$

This is also an attractive force and the force points along the positive $x$-direction. So, $vec{F}_{23} = 303.41:hat{x}$

The net force on $q_2$ is

$vec{F}_2 = vec{F}_{21} + vec{F}_{23} = -101.14: hat{x} + 303.41: hat{x} = (-101.14 + 303.42) :hat{x} = 202.28:hat{x}$

So the magnitude of the net force acting on $q_2$ is $202.28:N$ and it points along the positive $x$ direction.

(b)

When the separation between charges is increased three times the magnitude of the force on $q_2$ decreases as follows.

$F’_2 = dfrac{F_2}{3^2} = dfrac{202.28}{9} = 22.48:N$

This is because the force is inversely proportional to the square of the separation between them.

The direction remains unchanged.