The equations of motion for you ($x^{(1)}$) and your friend ($x^{(2)}$) are, respectively,

$$
begin{align*}
x_{f}^{(1)}&=x_{i}^{(1)}+v^{(1)}t\
&=left(4.20 frac{text{m}}{text{s}}right)times t tag{1}\\
\
\
\
x_{f}^{(2)}&=x_{i}^{(2)}+v^{(2)}t\
&=7.8 text{m}+left(2.30 frac{text{m}}{text{s}}right)times t tag{2}\\
end{align*}
$$

The point at which the two of you will meet is $x_{f}^{(2)}$. Denoting the time your friend stops walking after you step onto the walkway by $t_{s}$, and plugging that value in equation (2), we obtain

$$
begin{align*}
x_{f}^{(2)}&=7.8 text{m}+left(2.30 frac{text{m}}{text{s}}right)times 2.2 text{s}\
&=7.8 text{m}+5.06 text{m}\
&=12.9 text{m}\
end{align*}
$$

Here, we used $textbf{the rule for addition and subtraction to determine the number of significant figures in the answer.}$

To find out how long it takes you to catch up with your friend, plug in the value of $x_{f}^{(2)}$ into $x_{f}^{(1)}$ in equation (1), and solve for $t$:

$$
begin{align*}
t&=dfrac{x_{f}^{(1)}}{v^{(1)}}\
&=dfrac{12.9 text{m}}{4.20 frac{text{m}}{text{s}}}\
&=quadboxed{3.07 text{s}}\
end{align*}
$$

When writing the final result, we used $textbf{the rule for multiplication and division to determine the number of significant figures.}$

$$
begin{align*}
boxed{t=3.07 text{s}}\
end{align*}
$$

$textbf{(a)}$      Setting the car’s initial position $x_{i}^{(c)}$ to zero at $t=0$, and taking your direction of motion to be positive, the equation of motion is

$$
x_{f}^{(c)}=x_{i}^{(c)}+v^{(c)}t
$$

$boxed{x_{f}^{(c)}=left(26 frac{text{m}}{text{s}}right)times t}$

The truck’s initial position is $x_{i}^{(t)}=420 text{m}$, and its velocity is negative because it’s moving in the opposite direction. Therefore, the equation of motion of the truck is

$$
x_{f}^{(t)}=x_{i}^{(t)}+v^{(t)}t
$$

$boxed{x_{f}^{(t)}=420 text{m}-left(31 frac{text{m}}{text{s}}right)times t}$

textbf{(b)} quad To plot the two equations on a position-time graph, calculate a few pairs of data points for each line. The equations are already in the slope-intercept form of the line\
$$y=a+bx$$
$$bigDownarrow$$
[x_{f}^{(c),(t)} = x_{i}^{(c),(t)}+v^{(c),(t)}t]

so you just have to plug in arbitrary values of $x_{f}^{(c),(t)}$ to get the values of $t$, or vice versa.\

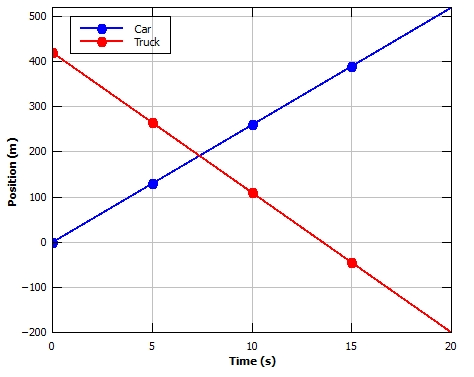
The positions of both vehicles for 4 different values of $t$ are given in the table, below which is the position-time graph.\
begin{center}
begin{tabular}{|c|c|c|}
hline
textbf{Time (s)} & textbf{Car position (m)} & textbf{Truck position (m)}\
hline
0&0&420\
hline
5&130&265\
hline
10&260&110\
hline
15&390&-45\
hline
20&520&-200\
hline
end{tabular}
end{center}

$textbf{(c)}$      $textbf{When objects are at the same location, their graphs intersect.}$ This is the case when you and the truck pass one another. To find the time at which you have the same location, we set the equations of motion to be equal, and solve for $t$:

$$
begin{align*}
x_{f}^{(c)}&=x_{f}^{(t)}\
26 frac{text{m}}{text{s}}times t&=420 text{m}-31 frac{text{m}}{text{s}}times t\
57 frac{text{m}}{text{s}}times t&=420 text{m}\
t&=dfrac{420 text{m}}{57 frac{text{m}}{text{s}}}\
&=7.368421053 text{s}\
&=quadboxed{7.4 text{s}}\
end{align*}
$$

As always, the rule for multiplication and division for significant figures was used when writing the final result.

$$
begin{align*}
textbf{(a)} quad &text{The equation of motion for the car:}quadquadboxed{x_{f}^{(c)}=left(26 frac{text{m}}{text{s}}right)times t}\
&text{The equation of motion for the truck:}quadboxed{x_{f}^{(t)}=420 text{m}-left(31 frac{text{m}}{text{s}}right)times t}\
\
\
\
textbf{(b)} quad &text{Click to see the position-time graph.}\
\
\
\
textbf{(c)} quad &boxed{t=7.4 text{s}}\
end{align*}
$$