Home Page Textbooks Physics Page 586: Lesson Check

Physics

1st Edition

Walker

ISBN: 9780133256925

Textbook solutions

All Solutions

Page 586: Lesson Check

Exercise 26

Step 1

1 of 2

We know that $f=frac{1}{2}R$, the focal point will be $R/2$ distance away in front of the mirror.

Result

2 of 2

$$
R/2
$$

Exercise 27

Step 1

1 of 2

The focal point will be $R/$ distance behind the mirror. That is at $-R/2$

Result

2 of 2

$$
-R/2
$$

Exercise 28

Step 1

1 of 1

The three quantities are 1) focal length ($f$), 2) object distance ($d_o$), 3) image distance ($d_i$).

Exercise 29

Step 1

1 of 1

begin{tabular}{|c|c|}
hline
Real image & Virtual imagetabularnewline
hline
hline
real image can be projected on screen & virtual image can not be projected on screentabularnewline
hline
real image form in front of mirror & virtual image forms behind the mirrortabularnewline
hline
real image are inverted & virtual image is uprighttabularnewline
hline
end{tabular}

Exercise 30

Step 1

1 of 2

Concave mirror produce real image if the object distance is greater than the focal length of the mirror. If the object distance is less than the focal length then concave mirror produce virtual image.
Convex mirror always produce virtual image.

Result

2 of 2

Concave mirror produce real and virtual image(depending on the case) and convex mirror always produce virtual image.

Exercise 31

Step 1

1 of 2

The concave surface points towards the satellite. The concave surface will focus the incoming signal from satellite on the receiver, and hence increase the signal strength on the receiver.

Result

2 of 2

The strength will increase.

Exercise 32

Step 1

1 of 2

$$
tt{According to {color{#4257b2}{Table 16.1}} a convex surface should produce an upright, reduced, virtual image, this is due to the convex surface behavior in reflecting light illustrated in the {color{#4257b2}{Figure 16.25}} as all principle rays are scattered and only their extensions can intersect behind the mirror.}
$$

Result

2 of 2

$$
tt{upright,reduced,virtual image}
$$

Exercise 33

Step 1

1 of 4

The focal length for a convex mirror of radius $R$ is given by

$$
begin{align*}
f = -frac{1}{2}R
end{align*}
$$

While the focal length for a concave mirror of radius $R$ is given by

$$
begin{align*}
f = frac{1}{2}R
end{align*}
$$

Step 2

2 of 4

$textbf{(a)}$

We plug in the value $R = 0.86;text{m}$ for the convex mirror focal length equation.

$$
begin{align*}
f = -frac{1}{2}(0.86;text{m}) = boxed{-0.43;text{m}}
end{align*}
$$

Step 3

3 of 4

$textbf{(b)}$

We plug in the value $R = 0.86;text{m}$ for the concave mirror focal length equation.

$$
begin{align*}
f = frac{1}{2}(0.86;text{m}) = boxed{0.43;text{m}}
end{align*}
$$

Result

4 of 4

(a) $f = -0.43$ m

(b) $f = 0.43$ m

Exercise 34

Step 1

1 of 2

So the focal length of the mirror is $f=15$ cm.

Hence the radius curvature is $R=2f=2times (15 {rm cm})=30$ cm

Result

2 of 2

30 cm.

Exercise 35

Step 1

1 of 1

Exercise 36

Step 1

1 of 2

$tt{the mirror equation states:$frac{1}{f}=frac{1}{d_o}+frac{1}{d_i}$}$

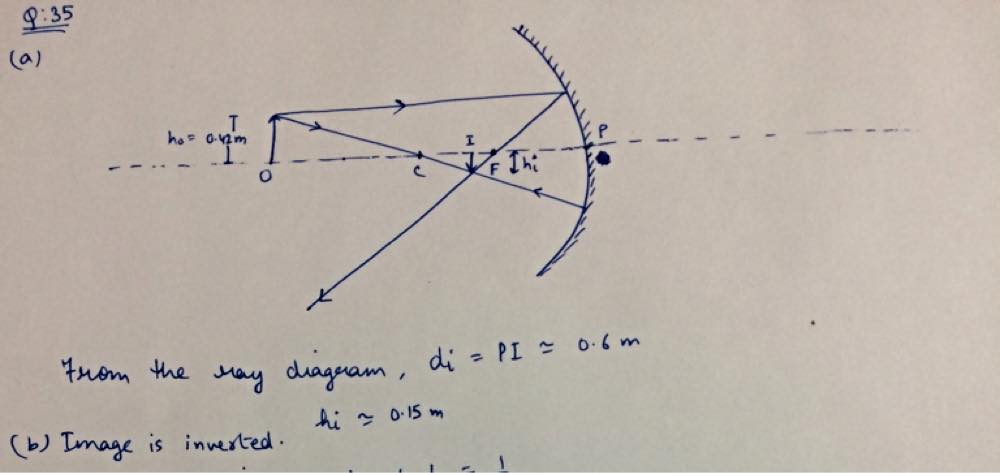
The mirror is concave $Rightarrow f>0$

$d_o>fRightarrow$ The image is real $Rightarrow d_i>0$

$frac{1}{d_i}=frac{1}{f}-frac{1}{d_o}=frac{d_o-f}{d_of}Rightarrow d_i=frac{d_of}{d_o-f}=frac{2*0.5}{2-0.5}=boxed{0.67m}$

The magnification equation states:

$$
m=-frac{d_i}{d_o}=boxed{-0.33}
$$

$$
m=frac{h_i}{h_o}Rightarrow h_i=m*h_o=(-0.33)*42=boxed{14cm}
$$

Result

2 of 2

$$
d_i=0.67m,text{m}=-0.33,h_i=14cm
$$

unlock

All Solutions

Page 586: Lesson Check

Haven't found what you were looking for?

Search for samples, answers to your questions and flashcards