
All Solutions
Page 557: Assessment
tt{when the source is moving towards the observer, the frequency observed is:$$f_1=f_{source}(1+frac{v_{source}}{c})$$}
$$
$$
tt{when the source is moving away from the observer, the frequency observed is:$$f_2=f_{source}(1-frac{v_{source}}{c})$$}
$$
We have:
$$
begin{align*}
frac{f_1}{f_2}= frac{1+ frac{v_{source}}{c}}{1- frac{v_{source}}{c}}&=frac{c+v_{source}}{c-v_{source}}=2\
&Rightarrow c+v_{source}=2(c-v_{source})\
&v_{source}=frac{c}{3}
end{align*}
$$
tt{$v_{source}=frac{c}{3}$}
$$
$$
Rightarrowfrac{f_{observed}}{f_{source}}=(1 pm frac{v_{source}}{c})
$$
$tt{consequentially the term $(1 pm frac{v_{source}}{c})$ determines if the source is moving towards or from the observer:}$
$tt{if the sign is positive:$ frac{f_{observed}}{f_{source}}=(1 + frac{v_{source}}{c})>1$}$
$Rightarrow f_{observed}>f_{source}$: the source is moving towards the observer
$tt{if the sign is positive:$ frac{f_{observed}}{f_{source}}=(1 – frac{v_{source}}{c})<1$}$
$Rightarrow f_{observed}<f_{source}$: the source is moving away from the observer.
tt{ the sign applied to the term $(1 pm frac{v_{source}}{c})$ is the Doppler formula}
$$
distance between the sun and the Alpha Centauri is
$$
left(4.3 {rm ly}right)timesleft(9.46times10^{15} {rm frac{m}{ly}}right)=4.07times10^{16} {rm m}
$$
$$
t=frac{d}{c}=frac{left(4.5times10^{12} {rm m}right)}{left(3times10^{8} {rm m/s}right)}=1.5times10^{4} {rm s}
$$
1.5times10^{4} {rm s}
$$
$v_{s}=40.2 {rm m/s}$,
$$
f_{s}=10.525 {rm GHz}
$$
Unknown:
$$
Delta f=?
$$
Soluton
$$
Delta f=f_{S}left(frac{v_{s}}{c}right)=left(10.525 {rm GHz}right)frac{left(40.2 {rm m/s}right)}{left(3times10^{8} {rm m/s}right)}=1.41times10^{-6} {rm GHz}=1.41 {rm kHz}
$$
tt{(a)the star is moving away from earth, therefore the Doppler formula is:}
$$
$$
f_{observed}=f_{source}(1- frac{v_{source}}{c})=f_{source}(1- frac{36500*10^3}{3*10^8})
$$
$$
f_{observed}=0.88f_{source}
$$
We know that : $C= lambda f Rightarrow lambda= frac{c}{f}$, using the latter form we have:
$$
lambda_{observed}= frac {c}{f_{observed}}= frac{c}{0.88 f_{source}}= frac {lambda_{source}}{0.88}
$$
$Rightarrow lambda_{observed} > lambda_{source}$ $tt{the wavelength of the moving star spectrum are{ color{#4257b2}{Greater}} then if it was at rest relative to earth.}$
tt{(b) the factor by which the spectrum shifted is }
$$
$$
frac{f_{source}-f_{observed}}{f_{source}}=frac{f_{source}(1-0.88)}{f_{source}}=boxed{0.12}
$$
tt{(a) Greater, (b) 0.12}
$$
we know that:
$$
f_{observed}=0.85f_{source} Rightarrow frac {f_{observed}}{f_{source}}=(1 pm frac{v_{source}}{c})=0.85< 1
$$
Based on the above we conclude that $pm frac{v_{source}}{c} Rightarrow – frac{v_{source}}{c}$
Referring to the Dopper formula we conclude that the galaxy is $text{color{#4257b2}{moving away}}$ from earth
tt{(b) based on (a) we have :}
$$
$$
1- frac{v_{source}}{c}=0.85 Rightarrow frac{v_{source}}{c}=0.15 Rightarrow v_{source}=0.15c
$$
tt{(a) moving away , (b) $v_{source}=0.15c$}
$$
$$
begin{align*}
v = frac{d}{t}
end{align*}
$$
In the case of the experiment, the total travelled distance is $2d$. We find $d$ such $v = c$ and $Delta t = 0.2$ s and the error for the value of $d$ is no more that 15$%$.
$$
begin{align*}
c &= frac{2d}{Delta t} \ d &= frac{cDelta}{2}
end{align*}
$$
$$
begin{align*}
d = frac{left(3.0times 10^{8};frac{text{m}}{text{s}}right)(0.2;text{s})}{2} = 3times 10^{7};text{m}
end{align*}
$$
$$
begin{align*}
d = frac{3times 10^{7};text{m}}{0.15} = boxed{2times 10^{8};text{m}}
end{align*}
$$
texttt{Assuming that $t$ is the time needed for the mirror to accomplish an eighth of a revolution, we have:}
$$
$$
frac{frac{1}{8}Rev}{t}=frac{528Rav}{1s} Rightarrow t= frac{frac{1}{8}Rev}{528Rev}=2.37*10^{-4}s
$$
The calculated speed of light is then:
$$
C=frac{71*10^3m}{2.37*10^{-4}}=3.00*10^8 frac{m}{s}
$$
3.00*10^8 frac{m}{s}
$$
$$
begin{align}
frac{f_{observed}}{f_{source}}=(1 pm frac{v_{source}}{c})
end{align}
$$
we know that $c=lambda f Rightarrow f=frac{c}{lambda}$, as result we can write (1) as :
$$
frac{lambda_{source}}{lambda_{observed}}=1 pm frac{v_{source}}{c}=frac{590}{550}=1.07>1
$$
As result we conclude that $1 pm frac{v_{source}}{c} =1 + frac{v_{source}}{c}$
$$
frac{lambda_{source}}{lambda_{observed}}=1 + frac{v_{source}}{c}
$$
$$
v_{source}=(frac{lambda_{source}}{lambda_{observed}}-1)c=(frac{590}{550}-1)*3*10^8=boxed{2.18*10^7 frac{m}{s}}
$$
based on the Doppler formula the motorist should be travelling $text{color{#4257b2}{towards}}$ the light
tt{(a)$v_{source}=2.18*10^7 frac{m}{s}$,(b) Towards the light}
$$
$tt{Time needed for the girl to hear the home run:}$
$$
t_1=frac{d_1}{v_{sound}}=frac{115m}{343 frac{m}{s}}=0.34s
$$
$$
tt{Time needed for the father to hear the home run:}
$$
$$
t_2=frac{d_2}{c}=frac{132*10^3m}{3*10^8 frac{m}{s}}=4.4*10^{-4}s
$$
$$
tt{$ t_1>t_2 Rightarrow$ the father will hear the home run first}
$$
tt{the father will hear the home run first}
$$
tt{the Galaxy is receding from earth, therefore we will use this form of the Doppler formula:}
$$
$$
begin{align*}
f_{observed}&=f_{source}(1-frac{v_{source}}{c})\
&=5*10^{14}Hz(1-frac{3325*10^3frac{m}{s}}{3*10^8 frac{m}{s}})\
&=boxed{4.944*10^{14}Hz}
end{align*}
$$
4.944*10^{14}Hz
$$
tt{the spaceships are approaching each other therefore we will use this form of the Doppler formula: }
$$
$$
f_{observed}=f_{source}(1+frac{v_{source}}{c})
$$
$tt{we know that $c=lambda f Rightarrow lambda=frac{c}{f}$}$,consequentially:
$$
begin{align*}
frac{f_{observed}}{f_{source}}&=(1+frac{v_{source}}{c}) \
frac{lambda_{source}}{lambda_{observed}}&=(1+frac{v_{source}}{c}) \
lambda_{source}&=(1+frac{v_{source}}{c}) lambda_{observed}\
&=(1+frac{722.5*10^3 frac{m}{s}}{ 3*10^8frac{m}{s}})670.3\
&=boxed{671.9nm}
end{align*}
$$
tt{$lambda_{source}=671.9nm$}
$$
tt{the car is receding from the radar therefore we will use the following form of the Doppler formula:}
$$
$$
f_{observed}=f_{source}(1-frac{v_{source}}{c})
$$
$$
tt{In a first place,frequencies observed by the car experience the Doppler effect:}
$$
$$
f_{car}=f_{source}(1-frac{v_{source}}{c})
$$
$$
tt{In a second place,frequencies that are reflected by the car and observed by the radar also experience Doppler effect: }
$$
$$
f_{radar}=f_{car}(1-frac{v_{car}}{c})
$$
tt{knowing that $v_{source}=v_{car}$ (both refer to the relative speed between the two cars) we deduce:
$$
f_{radar}=f_{source}(1-frac{v_{source}}{c})(1-frac{v_{source}}{c})
$$
$$
f_{radar}=f_{source}(1-frac{v_{source}}{c})^2
$$
$$
f_{radar}=8*10^9(1-frac{44.5 frac{m}{s}}{3*10^8frac{m}{s}})^2
$$
$$
f_{radar}=boxed{7.99*10^9Hz}
$$
f_{radar}=7.99*10^9Hz
$$
tt{The Doppler formula states that:}
$$
$$
f_{observed}=f_{source}(1pmfrac{v_{source}}{c})
$$
$$
tt{$v_{source} text{ and } c$ are speeds therefore they are always positive,the sign before the term $frac{v_{source}}{c}$ determines if the object is moving towards or away from the observer \ }
$$
`$tt{moreover in this case $v_{source}$ which is the relative speed of the galaxy arm to the observer is not straight forward but rather a combination of the relative speeds, the relative speed of the arm to the center of the galaxy and the relative speed of the galaxy to the observer}$
$$
tt{(a)The arm is moving towards the earth:}
$$
$$
begin{align*}
f_{observed}&=f_{source}(1+frac{v_{source}}{c}) \
&=f_{source}(1+frac{abs{V-v}}{c}) \
&=8.23*10^{14}Hz(1+frac{abs{3.6*10^5frac{m}{s}-6.4*10^5frac{m}{s}}}{3*10^8frac{m}{s}})=boxed{8.237*10^{14}Hz}\
end{align*}
$$
$$
tt{(b)The arm is moving away from the earth:}
$$
$$
begin{align*}
f_{observed}&=f_{source}(1-frac{v_{source}}{c}) \
&=f_{source}(1-frac{abs{V+v}}{c}) \
&=8.23*10^{14}Hz(1-frac{abs{3.6*10^5frac{m}{s}+6.4*10^5frac{m}{s}}}{3*10^8frac{m}{s}})=boxed{8.202*10^{14}Hz}\
end{align*}
$$
tt{(a)$8.237*10^{14}Hz$,(b)$8.202*10^{14}Hz$}
$$
tt{An electromagnetic wave consists of an oscillating electric and magnetic fields, these two field are perpendicular to each other, an electromagnetic wave can be produced naturally by an oscillating electron or oscillating current. }
$$
tt{oscillating electric and magnetic fields, oscillating electron or oscillating current. }
$$
tt{every electromagnetic is characterized by the following formula: $c= lambda f=constant$, meaning if $lambda uparrow$,$f downarrow$ and vice versa.\ we know that $f_{infared}lambda_{ultraviolet}}$}
$$
lambda_{infrared}>lambda_{ultraviolet}
$$
tt{every electromagnetic is characterized by the following formula: $c= lambda f=constant$, meaning if $lambda uparrow$,$f downarrow$ and vice versa.\ we know that $lambda_{red}>lambda_{blue} Rightarrow boxed{f_{red}<f_{blue}}$.}
$$
f_{red}<f_{blue}
$$
$$
Rightarrow lambda_{new}f_{new}=lambda f Rightarrow f_{new}=frac{lambda f}{lambda_{new}}=frac{lambda f}{2lambda}=boxed{frac{f}{2}}
$$
tt{Decrease by a factor of 2}
$$
tt{The human eye has three specific types of light-sensitive cells, all other colors that we perceive are a combination of these three colors with different amounts, these colors are called primary colors or additive colors which are Blue, Red, Green}
$$
tt{The three additive colors are Blue, Red, Green}
$$
tt{By subtracting specific color from the white light we can produce the desired colors, this is done through pigments, different pigments absorb some colors while reflecting others, The Three subtractive colors are Cyan; Magenta, and Yellow, when combining the three colors the result is black because we subtracted all colors from the white color }
$$
tt{The Three subtractive colors are Cyan; Magenta, Yellow}
$$
tt{by combining Blue and Yellow Light, we get White light.\by combining Blue and Green, we get Cyan light}
$$
tt{White,Cyan}
$$
tt{By combining Cyan and Yellow, We get White light. \By combining Cyan and Red, We get White light}
$$
tt{White,White}
$$
tt{Half a TV = 1500000 Pixels\
White = Blue+Red+Grean.\
Blue=Blue\
$$Blue=white_{half}+blue_{half}=1500000+1500000=3000000 dots$$
$$Red=white_{half}1500000dots$$
$$Green=white_{half}1500000dots$$}
$$
tt{Blue=3000000dots,Red=1500000dots;Green=1500000dots}
$$
tt{Half a TV = 1500000 Pixels\
Magenta= Blue+Red.\
Green=Green.\
$$Blue=Magenta_{half}=1500000dots$$
$$Red=Magenta_{half}=1500000dots$$
$$Green=Green_{half}1500000dots$$}
$$
tt{Blue=1500000dots,Red=1500000dots,Green=1500000}
$$
tt{Every electromagnetic wave is characterized by the following formula: }
$$
$$
c=lambda f Rightarrow f=frac{c}{lambda}=frac{3*10^8}{460*10^{-9}}=boxed{6.52*10^{14}text{Hz}}
$$
6.52*10^{14}text{Hz}
$$
$$
tt{$$N=frac{1*10^{-3}}{590*10^{-9}}=boxed{1694}$$}
$$
tt{N=1694}
$$
tt{Every electromagnetic wave obeys the following formula: $$c=lambda f Rightarrow lambda=frac{c}{f}=frac{3*10^8}{1.25*10^8}=boxed{2.4m}$$}
$$
tt{$lambda=2.4m$}
$$
$$
tt{(a)UV-B wave range is (280nm-320nm), calculating the range of frequencies:}
$$
$$
f=frac{c}{lambda}=frac{3*10^8}{280*10^{-9}}=10.71*10^{14}text{Hz}
$$
$$
f=frac{c}{lambda}=frac{3*10^8}{320*10^{-9}}=9.38*10^{14}text{Hz}
$$
tt{(b) $lambda=frac{c}{f}=frac{3*10^8}{7.9*10^{14}}=380nm Rightarrow$this wave belongs to the UV-A wave range.
tt{(a) UV-B frequency range $(9.38*10^{14}text{Hz}-10.71*10^{14}text{Hz})$,(b) UV-A wave range}
$$
$$
Rightarrow lambda=frac{c}{f}=frac{3*10^8}{10*10^3}=30000m
$$
lambda=30000m
$$
from medium to medium $f=constant, vdownarrow Rightarrow lambda downarrow$ $text{color{#4257b2}{decrease}}$
tt{(b) $f=constant= frac{c}{lambda_1}=frac{frac{3}{4}c}{lambda_2}Rightarrow lambda_2=boxed{frac{3}{4}lambda_1}$
tt{(a)Decrease,(b)$frac{3}{4}$}
$$
$$
tt{(b) Every electromagnetic wave obeys to following formula: $c=lambda f Rightarrow f=frac{c}{lambda}$ }
$$
$$
f_{red}=frac{c}{lambda_{red}}=frac{3*10^8}{680*10^{-9}}=4.41*10^{14}text{Hz}
$$
$$
f_{blue}=frac{c}{lambda_{blue}}=frac{3*10^8}{470*10^{-9}}=6.38*10^{14}text{Hz}
$$
tt{(a)Violet,(b) $f_{red}=4.41*10^{14}text{Hz},f_{blue}=6.38*10^{14}text{Hz}$}
$$
$$
Rightarrow T=frac{lambda}{c}=frac{29*10^9}{3*10^8}=96.7s
$$
tt{$T=96.7s$}
$$
$$
Rightarrow L=frac{1}{2}lambda=frac{1}{2}frac{c}{f}=frac{3*10^8}{2*6.6*10^7}=2.27text{m}
$$
tt{2.27m}
$$
$$
L=frac{1}{4}lambda=frac{1}{4}frac{c}{f}=frac{3*10^8}{4*880*10^3}=85.2text{m}
$$
tt{$L$=85.2m}
$$
tt{Let’s Denote the height of the antenna $L$}
$$
$$
L=frac{1}{4}lambda=frac{1}{4}frac{c}{f} Rightarrow f=frac{c}{4L}=frac{3*10^8}{4*112}=6.7*10^5text{Hz}
$$
tt{$f=6.7*10^5text{Hz}$}
$$
tt{transmission axis of the sunglasses and the watch are perpendicular}
$$
tt{with the aid of a polarized light directed at the sheet, we proceed by rotating the sheet, when the light observed through the polarized sheet reach the maximum, the polarized light and the transmission axis of the sheet are parallel}
$$
tt{using a polarized light}
$$
tt{Sound is a longitudinal wave meaning they vibrate along the direction of their propagation, therefore can not be polarized }
$$
tt{Sound waves can not be polarized }
$$
tt{(a)In both cases half of the unpolarized light intensity is transmitted through the first polarizer, moreover the second polarizer is positioned at the same relative angle to the first polarizer $theta$, consequentially the final transmitted light has the same intensity in both cases,\(b) A}
$$
tt{(a)The Same,(b) A}
$$
Case A:$I_{fa}=I_i cos^2(theta – alpha)cos^2( theta)$
Case B:$I_{fb}=I_i cos^2(alpha)cos^2 (theta)$
Having the same final intensity implies the following $Rightarrow I_{fa}=I_{fb} Rightarrow cos^2(theta – alpha)=cos^2(alpha)$ consequentially :
$$
begin{align*}
cos(theta – alpha)=cos(alpha) &text{ or } `cos(theta – alpha)=-cos(alpha)
end{align*}
$$
$$
tt{in the $[0,pi] text{ domain} $}
$$
$$
begin{align*}
theta-alpha=alpha &text{ or } theta – alpha =pi- alpha\
`alpha =boxed{frac{theta}{2}} &text{ or } theta =pi Rightarrow text{ absurd}
end{align*}
$$
tt{$alpha = frac{theta}{2}$}
$$
$$
I_f=I_i cos^2theta =0.55cos^235=boxed{0.37 frac{W}{m^2}}
$$
I_f=0.37frac{W}{m^2}
$$
tt{according to the textit{Law of Malus} :}
$$
$$
I_f=I_icos^2thetaRightarrow frac{I_f}{I_i}=cos^2 theta
$$
The reflected light from the water is horizontal whereas the person is leaning by $27.5^o$ to the vertical, resulting in an angle of incidence $theta=90-27.5=62.5^o$, plugging the value Into the former formula we have :
$$
frac{I_f}{I_i}=cos^2 62.5=0.21frac{W}{m^2}
$$
frac{I_f}{I_i}=0.21frac{W}{m^2}
$$
tt{Let $I_1$ be the light intensity of the incident light from the first polarizer on the second polarizer, we have: }
$$
$$
I_f=I_1cos^2theta
$$
Since the incident light is unpolarized , we have :
$$
I_1=frac{1}{2}I_i
$$
consequentially:
$$
I_f=frac{1}{2}I_icos^2thetaRightarrow frac{I_f}{I_i}=frac{1}{2}cos^250=boxed{0.207frac{W}{m^2}}
$$
frac{I_f}{I_i}=0.207frac{W}{m^2}
$$
tt{From Question 90 we deduced that $frac{I_f}{I_i}=frac{1}{2}cos^2theta$, the intensity of the light transmitted needs to be the tenth of the intensity of the incident light meaning $frac{I_f}{I_i}=frac{1}{10}$:}
$$
$$
frac{I_f}{I_i}=frac{1}{2}cos^2theta=frac{1}{10}
$$
$$
cos^2theta=frac{1}{5}
$$
$$
costheta=frac{1}{sqrt{5}}
$$
$$
theta=arccos{frac{1}{sqrt{5}}}
$$
$$
theta=boxed{63.43^o}
$$
theta=63.43^o
$$
$$
begin{align*}
I_{text{f}} = frac{1}{2}I_{text{i}}
end{align*}
$$
$$
begin{align*}
I_{text{f}} = frac{1}{2}I_{text{i}} cos^{2} theta
end{align*}
$$
tt{(a)Let’s suppose that the first polarizer is vertical, the two polarizers are crossed therefore the second polarizer must be horizontal, and in between is the solution to be tested. Let’s denote $alpha$ the angle between the first and the polarizer, According to textit{Law of Malus} we have:}
$$
$$
I¨_{solution}=I_icos^2(alpha)
$$
The angle between the axis of transmission of the solution and the second polarizer is $90^o-alpha$applying the $textit{Law of Malus}$ again between the solution and the second polarizer we have:
$$
I_f=I_{solution}cos^2(90-alpha)
$$
we can then deduce:
$$
I_f=I_icos^2(alpha)cos^2(90-alpha) (1) Rightarrow frac{I_f}{I_i}=cos^2(alpha)cos^2(90-alpha)
$$
$tt{for I-leucine: $frac{I_f}{I_i}=cos^2(-0.55)cos^2(90+0.55)=0.302frac{W}{m^2}$}$
$tt{for d-glutamic:$frac{I_f}{I_i}=cos^2(0.62)cos^2(90-0.62)=0.384frac{W}{m^2}$}$
$tt{textcolor{#4257b2}{d-glutamic}}$ transmits greater light intensity.
$$
I_f=frac{1}{2}I_fcos^2(90-alpha)
$$
then we apply the new formula to both solutions:
for I-leucine: $I_f=frac{1}{2}12.5cos^2(90+0.55)=1.891frac{W}{m^2}$
for d-glutamic: $I_f=frac{1}{2}12.5cos^2(90-0.62)=2.403frac{W}{m^2}$
tt{(a) d-glutamic transmits greater light intensity, (b) I-leucine $I_f=1.891frac{W}{m^2},d-glutamic I_f=2.403frac{W}{m^2}$ }
$$
tt{(a) the incident light is unpolarized therefore the transmitted light intensity at point A is:}
$$
$$
I_A=boxed{frac{1}{2}I_i}
$$
tt{(b) The transmitted light intensity at point B follow $textit{Law of Malus}$:
$$
I_B=I_Acos^2theta_2=frac{1}{2}I_icos^2theta_2=frac{1}{2}I_icos^230=boxed{frac{3}{8}I_i}
$$
tt{(c) The transmitted light intensity at point C follow $textit{Law of Malus}$:
$$
I_C=I_Bcos^2theta_3=frac{1}{2}I_icos^2theta_2cos^2(theta_3-theta_2)=frac{1}{2}I_icos^230cos^260=boxed{frac{3}{32}I_i}
$$
tt{(d) if filter 2 is removed no light will be transmitted, we can prove this by writing the new $I_C$ formula :
$$
I_C=I_Acos^2theta_3=frac{1}{2}I_icos^2theta_3=frac{1}{2}I_icos^290=boxed{0}
$$
tt{(a)$frac{1}{2}I_i$,(b)$frac{3}{8}I_i$,(c)$frac{3}{32}I_i$,(d) $0$}
$$
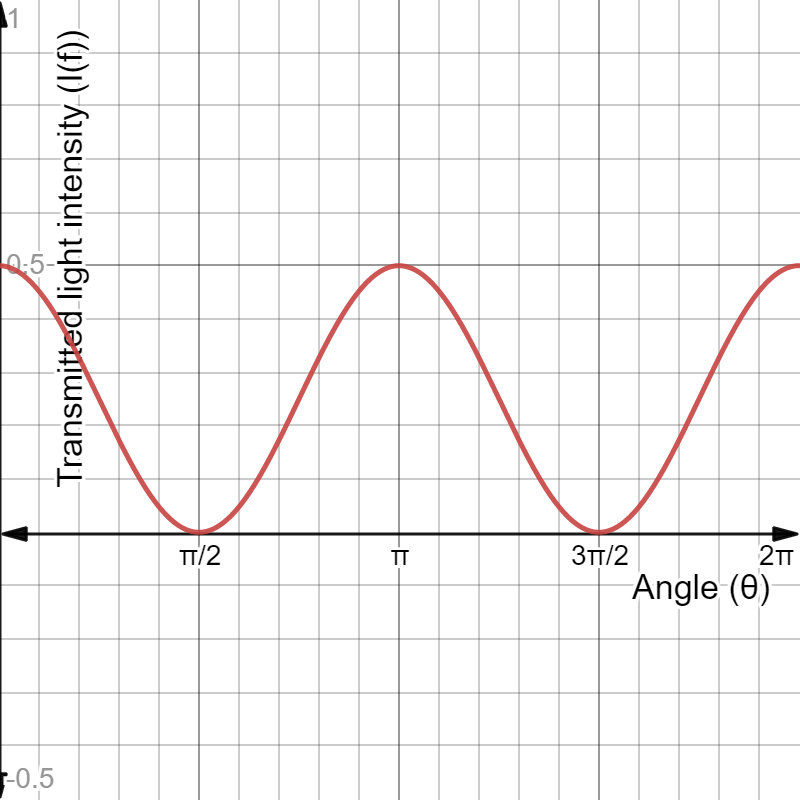
tt{(a) From the previous Exercise we have already established that:}
$$
$$
I_f=frac{1}{2}I_icos^2theta_2cos^2(theta_3-theta_2)=frac{1}{2}I_icos^230cos^2(theta_3-30)=frac{3}{8}I_icos^2(theta_3-30)
$$
In this part we will generalize$theta_3$ to be a random angle with the vertical named $theta$, the equation becomes:
$$
I_f=frac{3}{8}I_icos^2(theta-30) Rightarrow frac{I_f}{I_i}=frac{3}{8}cos^2(theta-30)
$$
$$
cos^2(theta-30)=1
$$
$$
begin{align*}
cos(theta-30)=1 &text{ or } cos(theta-30)=-1\
theta-30=0 &text{ or } theta-30=180\
theta-30=0 &text{ or } theta-30=180\
theta=30 &text{ or } theta=210
end{align*}
$$
tt{(a)$frac{I_f}{I_i}=frac{3}{8}cos^2(theta-30)$,(b) click for Graph, (c) $theta={30,210}$}
$$
setlength{arrayrulewidth}{1mm}
setlength{tabcolsep}{18pt}
begin{tabular}{ |p{3cm}|p{3cm}| }
hline
textbf{ wave} & textbf{wavelength range} \
hline
(A)Infrared& $700nm-10^6nm$\
(B)X-rays& $0.01nm-10nm$\
(C)Green Light& $510nm$\
(D)Radio waves& $10^6nm-10^{12}nm$\
hline
end{tabular}
end{center}
begin{center}
tt{we conclude that}$B<C<A<D$
end{center}
tt{$B<C<A<D$}
$$
since $lambda$ and $f$ are both scalars and the formula represents a constant scalar product then
if $fuparrow$ then $lambda downarrow$ but $v$ keeps the same value.
tt{the speed remains constant }
$$
$$
tt{(b) every electromagnetic wave obeys to the following formula : $c=lambda f$}
$$
$$
Rightarrow f=frac{c}{lambda}=frac{3*10^8}{650*10^{-9}}=4.61*10^{14}text{Hz}
$$
tt{(a)red light,(b)$4.61*10^{14}$Hz}
$$
Light Reflectors: light bounces back when it encounters a surface therefore light reflectors do not necessarily produce light, some characteristics to have a good reflective surface are to be smooth(so the reflected light is not scattered) and opaque(so light does not go through the object).
$tt{in a physics classroom:}$
(a)Objects that emit light: light bulb, computer monitor
(b)Objects that reflect light: Desk, Board
tt{(a)Light bulb, computer monitor (b) Desk, Board}
$$
in music an octave represents a doubling in frequency for example the distance between 20Hz and 40Hz is an octave, between 20Hz and 80Hz is 2 octaves
$textbf{Explanation:}$ ($80=40*2=(20*2)*2=20*2^2 Rightarrow frac{80}{20}=2^2Rightarrow log_2frac{80}{20}=2=Number of octaves$)
We can then establish that the number of octaves $N=log_2frac{x}{y}$
for the Human hearing range: $N=log_2frac{20*10^3}{20}=boxed{9.97}$
for the Human vision range: $N=log_2frac{770}{430}=boxed{0.84}$
tt{Human hearing range:9.97, Human vision range 0.84}
$$
$tt{We mix Cyan and Magenta to create the Blue color}$.
$tt{We mix Yellow and Cyan to create the Green Color}$.
tt{To create Blue we mix Cyan and Magenta, To create Green we mix Yellow and Cyan}
$$
tt{one way to figure out if the Sunglasses lenses are polarized, is by directing a polarized light at the lenses vertically and then change the angle between the sunglasses supposed transmission axis and the vertical. If the light intensity perceived through the sunglasses does not change then the glasses are not polarized }
$$
tt{by using a polarized light and observing if there is a change in the light intensity }
$$
$$
Rightarrow lambda= frac{c}{f}=frac{3*10^8}{1.5*10^{19}}=2*10^{-11}m=0.02nm
$$
lambda=0.02nm
$$
tt{to Determine the number of hydrogen atoms $N$ that can fit, end to end, in one wavelength of violet light, we divide the wavelength$lambda$ by the diameter of the hydrogen atoms$D_h$: }
$$
$$
N=frac{lambda}{D_h}=frac{410}{0.1}=boxed{4100}
$$
N=4100
$$
$tt{(b) if the light is vertically polarized then the angle of incidence $theta-0=theta$, according to the textit{Law of malus} $I_f=I_icos^2alpha$ in this case $ Rightarrow I_f=I_icos^2theta $, for $theta=0,I_f=I_i$, for $theta=90,I_f=0 Rightarrow$ Magenta Curve}$
$tt{(c) if the light is vertically polarized then the angle of incidence $90-theta$, according to the textit{Law of malus} $I_f=I_icos^2alpha$ in this case $ Rightarrow I_f=I_icos^2(90-theta) $, for $theta=90,I_f=0$, for $theta=90,I_f=I_i Rightarrow$ Blue Curve}$
tt{(a) Green,(a) Magenta,(c) Blue}
$$
tt{in 3D cinemas, two superimposed polarized images are projected on the same screen, the viewer, on the other hand, wears headsets with each one of the lenses being polarized to match the polarization of one of the projections, therefore each eye is perceiving a slightly different perspective of the image, creating the 3D illusion. }
$$
tt{using polarized filters and superimposed polarized images creates the 3D illusion }
$$
$$
c=lambda f Rightarrow lambda=frac{c}{f}=frac{3*10^8}{750*10^3}=400m
$$
lambda=400m
$$
tt{First let’s put a general formula that determines the light intensity transmission factor $frac{I_f}{I_i}$, Let $theta_1$ be the angle of transmission of the first polarizer,$theta_2$ the angle of transmission of the second polarizer(both angles are relative to the vertical) and $I_1$ the light intensity transmitted by the first polarizer, According to the tt{Law of Malus}: }
$$
$$
I_f=I_1cos^2(theta_2-theta_1)
$$
We know that the original incident light is unpolarized, therefore:
$$
I_1=frac{1}{2}I_i Rightarrow I_f=frac{1}{2}I_icos^2(theta_2 -theta_1)Rightarrow frac{I_f}{I_i}=boxed{frac{1}{2}cos^2(theta_2 -theta_1)}
$$
case A: $frac{I_f}{I_i}=frac{1}{2}cos^2(theta_2 -theta_1)=frac{1}{2}cos^2(90 -30)=0.125$
case B: $frac{I_f}{I_i}=frac{1}{2}cos^2(theta_2 -theta_1)=frac{1}{2}cos^2(30-(-60))=0$
case C: $frac{I_f}{I_i}=frac{1}{2}cos^2(theta_2 -theta_1)=frac{1}{2}cos^2(-30-30)=0.125$
case D: $frac{I_f}{I_i}=frac{1}{2}cos^2(theta_2 -theta_1)=frac{1}{2}cos^2(30-0)=0.375$
$$
boxed{B<C=A<D}
$$
tt{B<C=A<D}
$$
tt{We have $c=frac{d}{t}$ by introducing the uncertainty factor into the formula, we substitute $d$ and $t$ with $Delta d$ and $Delta t$ }
$$
$$
c=frac{Delta d}{Delta t} Rightarrow Delta d=cDelta t =3*10^8*0.030*10^{-9}=9*10^{-3}m
$$
Delta d= 9*10^{-3}m
$$
we also know that every electromagnetic wave obeys to the following formula $c=lambda f Rightarrow f=frac{c}{lambda}$
Substituting $f$ in the Doppler formula we obtain:
$$
frac{c}{lambda_{observed}}=frac{c}{lambda_{source}}(1pmfrac{v_{source}}{c})
$$
$$
frac{lambda_{source}}{lambda_{observed}}=1pmfrac{v_{source}}{c}
$$
since the wave length of the observed wave is longer than the original one we can denote it $lambda_beta +deltalambda$ The Doppler formula then becomes:
$$
frac{lambda_{beta}}{lambda_beta+deltalambda}=1pmfrac{v_{source}}{c}<1
$$
therefore the sign in term $(1pmfrac{v_{source}}{c})$ should be negative, producing the final version of the formula:
$$
frac{lambda_{beta}}{lambda_beta+deltalambda}=1-frac{v_{source}}{c} Rightarrow v_{source}= (1-frac{lambda_{beta}}{lambda_beta+deltalambda})c=(1-frac{486*10^{-9}}{(486+20)*10^{-9}})*3*10^8=1.19*10^7m
$$
v_{source}=1.19*10^7m
$$
if $d downarrow$ then $t downarrow$, on the other hand, we can express the angular speed of the mirror as :
$$
w=frac{Revolution}{t}
$$
assuming that the mirror needs to cover the same angular displacement in the experiment($frac{1}{8}Rev$),t if $downarrow$ then$boxed{wuparrow}$
(b) Calculating the angular speed:
$$
w=frac{Revolitons}{t}=frac{Revolitons*c}{d}=frac{frac{1}{8}*3*10^8}{2*20.5*10^3}=914 frac{Rev}{s}
$$
tt{(a)the angular velocity should be increased, (b)$w=914frac{Rev}{s}$ }
$$
$$
I_f=I_icos^2theta
$$
$$
frac{I_f}{I_i}=cos^2theta
$$
$$
sqrt{frac{I_f}{I_i}}=costheta
$$
$$
boxed{arccos{sqrt{frac{I_f}{I_i}}}}=theta
$$
$$
Rightarrow theta=arccos{sqrt{frac{212}{825}}}=boxed{59.5^o}
$$
(b)We know that $theta_1-theta=90Rightarrow theta_1=149.5^o$
applying the $textit{Law of Malus}$ for the second eye:
$$
I_f=I_icos^2theta_1=825cos^2149.5=612 frac{W}{m^2}
$$
tt{(a)$theta=59.5^o$,(b)$I_f=612frac{W}{m^2}$}
$$
tt{the car is approching the radar therefore we will use the following form of the Doppler formula :}
$$
$$
f_{observed}=f_{source}(1+frac{v_{source}}{c})
$$
$$
tt{In a first place,frequencies observed by the car experience the Doppler effect:}
$$
$$
f_{car}=f_{source}(1+frac{v_{source}}{c})
$$
$$
tt{In a second place,frequencies that are reflected by the car and observed by the radar also experience Doppler effect: }
$$
$$
f_{radar}=f_{car}(1+frac{v_{car}}{c})
$$
tt{knowing that $v_{source}=v_{car}$ (both refer to the relative speed between the two cars) we deduce:
$$
f_{radar}=f_{source}(1+frac{v_{source}}{c})(1+frac{v_{source}}{c})
$$
$$
f_{radar}=f_{source}(1+frac{v_{source}}{c})^2
$$
$$
f_{radar}=9*10^9(1+frac{35 frac{m}{s}}{3*10^8frac{m}{s}})^2
$$
$$
f_{radar}=boxed{9.01*10^9Hz}
$$
tt{Referring to {color{#4257b2}{Figure 15.41}} and applying the textit{Law of Malus} we can establish the following : }
$$
$$
begin{align}
I_f=I_C=I_Bcos^2(theta_3-theta_2)\
I_B=I_Acos^2(theta_2)\
I_A=frac{1}{2}I_i
end{align}
$$
by substituting (3) into (2),we have:
$$
I_B=frac{1}{2}I_icos^2(theta_2)
$$
by substituting (2) into (1),we have:
$$
I_f=frac{1}{2}I_icos^2(theta_2)cos^2(theta_3-theta_2)
$$
$tt{(a) case 1:$I_f=frac{1}{2}1.6cos^2(25)cos^2(50-25)=boxed{0.540frac{W}{m^2}}$}$
$$
tt{(b) case 2:$I_f=frac{1}{2}1.6cos^2(50)cos^2(25-50)=boxed{0.272frac{W}{m^2}}$}
$$
tt{(a)$=I_f=0.540frac{W}{m^2}$,(b)$I_f=0.272frac{W}{m^2}$}
$$
tt{We know that we can obtain an intensity $I=10^3frac{W}{m^2}=1frac{kW}{m^2}$form solar power, we will proceed to calculate the energy density of $1m^2$over one month and considering the collector efficiency: }
$$
$$
E_{Density} =I*Delta t*eta=1*(25*8)0.25=50frac{kWh}{m^2}
$$
To determine $A$: the collector area needed to cover the house energy requirement, we proceed as follows:
$$
E_{consumed}=E_{Density}*ARightarrow A=frac{E_{consumed}}{E_{Density}}=frac{2*10^3}{50}=40m^2
$$
tt{$A=40m^2$}
$$
Based on the last formula we can deduce that if $f uparrow$ then $lambda downarrow$. Referring to $text{color{#4257b2}{Figure 15.8}}$ microwaves have lower frequencies than X-Ray $Rightarrow$ microwaves have a wavelength $text{color{#4257b2}{greater than}}$ X-Rays
tt{Microwaves and X-Ray have the same speed, microwaves have a greater wavelength }
$$
tt{ Answer D.}
$$
$$
c= lambda f Rightarrow f= frac{c}{lambda}=frac{3*10^8}{465*10^{-9}}=6.45*10^{14}text{Hz}
$$
tt{the answer C.}
$$
tt{intensity is the power per unit area, therefore, $I=frac{P}{A}$, on the other hand, Power is the rate of change of energy over time:$P=frac{E}{Delta t}$, Consequentially: }
$$
$$
E=PDelta t=IADelta t=1000*0.5*30=15000mJ
$$

