
Physics
1st Edition
Walker
ISBN: 9780133256925
Textbook solutions
Chapter 1: Introduction to Physics
Section 1.1: Physics and the Scientific Method
Section 1.2: Physics and Society
Section 1.3: Units and Dimensions
Section 1.4: Basic Math for Physics
Page 38: Assessment
Page 41: Standardized Test Prep
Page 19: Practice Problems
Page 21: Practice Problems
Page 22: Lesson Check
Page 27: Practice Problems
Page 28: Practice Problems
Page 29: Practice Problems
Page 32: Lesson Check
Chapter 2: Introduction to Motion
Section 2.1: Describing Motion
Section 2.2: Speed and Velocity
Section 2.3: Position-Time Graphs
Section 2.4: Equation of Motion
Page 66: Assessment
Page 71: Standardized Test Prep
Page 45: Practice Problems
Page 47: Practice Problems
Page 47: Lesson Check
Page 49: Practice Problems
Page 52: Practice Problems
Page 53: Lesson Check
Page 56: Practice Problems
Page 57: Lesson Check
Page 59: Practice Problems
Page 60: Practice Problems
Page 62: Practice Problems
Page 62: Lesson Check
Chapter 3: Acceleration and Acceleration Motion
Section 3.1: Acceleration
Section 3.2: Motion with Constant Acceleration
Section 3.3: Position-Time Graphs for Constant Acceleration
Section 3.4: Free Fall
Page 105: Assessment
Page 111: Standardized Test Prep
Page 76: Practice Problems
Page 78: Practice Problems
Page 79: Practice Problems
Page 81: Practice Problems
Page 81: Lesson Check
Page 83: Practice Problems
Page 85: Practice Problems
Page 88: Practice Problems
Page 90: Practice Problems
Page 91: Lesson Check
Page 93: Practice Problem
Page 95: Practice Problems
Page 96: Lesson Check
Page 100: Practice Problems
Page 101: Lesson Check
Chapter 4: Motion in Two Dimensions
Section 4.1: Vectors in Physics
Section 4.2: Adding and Subtracting Vectors
Section 4.3: Relative Motion
Section 4.4: Projectile Motion
Page 144: Assessment
Page 149: Standardized Test Prep
Page 114: Practice Problems
Page 117: Practice Problems
Page 119: Practice Problems
Page 120: Lesson Check
Page 126: Practice Problems
Page 127: Practice Problems
Page 133: Practice Problems
Page 135: Practice Problems
Page 138: Practice Problems
Page 140: Lesson Check
Chapter 5: Newton’s Laws of Motion
Section 5.1: Newton’s Laws of Motion
Section 5.2: Applying Newton’s Laws
Section 5.3: Friction
Page 180: Assessment
Page 187: Standardized Test Prep
Page 155: Practice Problems
Page 158: Practice Problems
Page 159: Practice Problems
Page 160: Lesson Check
Page 164: Practice Problems
Page 167: Practice Problems
Page 169: Lesson Check
Page 172: Practice Problems
Page 175: Practice Problems
Page 176: Lesson Check
Chapter 6: Work and Energy
Section 6.1: Work
Section 6.2: Work and Energy
Section 6.3: Conservation of Energy
Section 6.4: Power
Page 220: Assessment
Page 227: Standardized Test Prep
Page 191: Practice Problems
Page 193: Practice Problems
Page 196: Lesson Check
Page 196: Practice Problems
Page 199: Practice Problems
Page 201: Practice Problems
Page 203: Practice Problems
Page 204: Practice Problems
Page 205: Practice Problems
Page 206: Lesson Check
Page 209: Practice Problems
Page 211: Lesson Check
Page 213: Practice Problems
Page 214: Practice Problems
Page 215: Practice Problems
Page 216: Lesson Check
Chapter 7: Linear Momentum and Collisions
Section 7.1: Momentum
Section 7.2: Impulse
Section 7.3: Conservation of Momentum
Section 7.4: Collisions
Page 260: Assessment
Page 265: Standardized Test Prep
Page 230: Practice Problems
Page 233: Practice Problems
Page 233: Lesson Check
Page 235: Practice Problems
Page 236: Practice Problems
Page 240: Practice Problems
Page 241: Lesson Check
Page 245: Practice Problems
Page 247: Lesson Check
Page 252: Practice Problems
Page 254: Practice Problems
Page 256: Lesson Check
Chapter 8: Rotational Motion and Equilibrium
Section 8.1: Describing Angular Motion
Section 8.2: Rolling Motion and the Moment of Inertia
Section 8.3: Torque
Section 8.4: Static Equilibrium
Page 300: Assessment
Page 305: Standardized Test Prep
Page 269: Practice Problems
Page 271: Practice Problems
Page 272: Practice Problems
Page 275: Practice Problems
Page 275: Lesson Check
Page 277: Practice Problems
Page 280: Lesson Check
Page 284: Practice Problems
Page 286: Practice Problems
Page 287: Practice Problems
Page 289: Lesson Check
Page 294: Practice Problems
Page 295: Practice Problems
Page 296: Lesson Check
Chapter 9: Gravity and Circular Motion
Section 9.1: Newton’s Law of Universal Gravity
Section 9.2: Applications of Gravity
Section 9.3: Circular Motion
Section 9.4: Planetary Motion and Orbits
Page 336: Assessment
Page 341: Standardized Test Prep
Page 309: Practice Problems
Page 311: Practice Problems
Page 312: Lesson Check
Page 315: Practice Problems
Page 317: Practice Problems
Page 318: Practice Problems
Page 319: Lesson Check
Page 323: Practice Problems
Page 326: Lesson Check
Chapter 10: Temperature and Heat
Section 10.1: Temperature, Energy, and Heat
Section 10.2: Thermal Expansion and Energy Transfer
Section 10.3: Heat Capacity
Section 10.4: Phase Changes and Latent Heat
Page 378: Assessment
Page 383: Standardized Test Prep
Page 345: Practice Problems
Page 347: Practice Problems
Page 349: Lesson Check
Page 349: Practice Problems
Page 352: Practice Problems
Page 357: Lesson Check
Page 361: Practice Problems
Page 362: Practice Problems
Page 365: Practice Problems
Page 366: Lesson Check
Page 373: Practice Problems
Page 374: Lesson Check
Chapter 11: Thermodynamics
Section 11.1: The First Law of Thermodynamics
Section 11.2: Thermal Processes
Section 11.3: The Second and Third Laws of Thermodynamics
Page 410: Assessment
Page 413: Standardized Test Prep
Page 388: Practice Problems
Page 391: Practice Problems
Page 392: Lesson Check
Page 394: Practice Problems
Page 396: Practice Problems
Page 399: Practice Problems
Page 400: Lesson Check
Page 404: Practice Problems
Page 406: Lesson Check
Chapter 12: Gases, Liquids, and Solids
Section 12.1: Gases
Section 12.2: Fluids at Rest
Section 12.3: Fluids in Motion
Section 12.4: Solids
Page 446: Assessment
Page 451: Standardized Test Prep
Page 417: Practice Problems
Page 419: Practice Problems
Page 421: Practice Problems
Page 423: Lesson Check
Page 425: Practice Problems
Page 427: Practice Problems
Page 428: Practice Problems
Page 431: Practice Problems
Page 434: Lesson Check
Page 436: Practice Problems
Page 439: Lesson Check
Page 441: Practice Problems
Page 442: Lesson Check
Chapter 13: Oscillations and Waves
Section 13.1: Oscillations and Periodic Motion
Section 13.2: The Pendulum
Section 13.3: Waves and Wave Properties
Section 13.4: Interacting Waves
Page 486: Assessment
Page 491: Standardized Test Prep
Page 455: Practice Problems
Page 458: Practice Problems
Page 459: Practice Problems
Page 461: Lesson Check
Page 461: Practice Problems
Page 464: Practice Problems
Page 467: Practice Problems
Page 469: Lesson Check
Page 472: Practice Problems
Page 474: Practice Problems
Page 475: Lesson Check
Page 477: Practice Problems
Page 480: Practice Problems
Page 482: Lesson Check
Chapter 14: Sound
Section 14.1: Sound Waves and Beats
Section 14.2: Standing Sound Waves
Section 14.3: The Doppler Effect
Section 14.4: Human Perception of Sound
Page 523: Assessment
Page 527: Standardized Test Prep
Page 495: Practice Problems
Page 496: Practice Problems
Page 500: Practice Problems
Page 501: Lesson Check
Page 503: Practice Problems
Page 504: Practice Problems
Page 506: Practice Problems
Page 506: Lesson Check
Page 510: Practice Problems
Page 511: Practice Problems
Page 512: Lesson Check
Page 514: Practice Problems
Page 516: Practice Problems
Page 517: Practice Problems
Page 519: Lesson Check
Chapter 15: The Properties of Lights
Section 15.1: The Nature of Light
Section 15.2: Color and the Electromagnetic Spectrum
Section 15.3: Polarization and Scattering of Light
Page 557: Assessment
Page 563: Standardized Test Prep
Page 530: Practice Problems
Page 532: Practice Problems
Page 534: Practice Problems
Page 536: Practice Problems
Page 538: Practice Problems
Page 544: Lesson Check
Page 547: Practice Problems
Page 549: Practice Problems
Page 553: Lesson Check
Chapter 16: Reflection and Mirrors
Section 16.1: The Reflection of Light
Section 16.2: Plane Mirrors
Section 16.3: Curved Mirrors
Page 590: Assessment
Page 595: Standardized Test Prep
Page 572: Practice Problems
Page 574: Lesson Check
Page 574: Practice Problems
Page 580: Practice Problems
Page 582: Practice Problems
Page 583: Practice Problems
Page 585: Practice Problems
Page 586: Lesson Check
Chapter 17: Refraction and Lenses
Section 17.1: Refraction
Section 17.2: Applications of Refraction
Section 17.3: Lenses
Section 17.4: Applications of Lenses
Page 629: Assessment
Page 635: Standardized Test Prep
Page 599: Practice Problems
Page 600: Practice Problems
Page 603: Practice Problems
Page 605: Lesson Check
Page 608: Practice Problems
Page 610: Practice Problems
Page 611: Lesson Check
Page 618: Practice Problems
Page 618: Lesson Check
Chapter 18: Interference and Diffraction
Section 18.1: Interference
Section 18.2: Interference in Thin Films
Section 18.3: Diffraction
Section 18.4: Diffraction Gratings
Page 668: Assessment
Page 673: Standardized Test Prep
Page 640: Practice Problems
Page 644: Practice Problems
Page 646: Practice Problems
Page 646: Lesson Check
Page 650: Practice Problems
Page 652: Practice Problems
Page 653: Lesson Check
Page 656: Practice Problems
Page 657: Practice Problems
Page 660: Practice Problems
Page 661: Lesson Check
Page 663: Practice Problems
Page 664: Lesson Check
Chapter 19: Electric Charges and Forces
Section 19.1: Electric Charge
Section 19.2: Electric Force
Section 19.3: Combining Electric Forces
Page 698: Assessment
Page 703: Standardized Test Prep
Page 678: Practice Problems
Page 682: Lesson Check
Page 688: Practice Problems
Page 689: Lesson Check
Page 692: Practice Problems
Page 694: Lesson Check
Chapter 20: Electric Fields and Electric Energy
Section 20.1: The Electric Field
Section 20.2: Electric Potential Energy and Electric Potential
Section 20.3: Capacitance and Energy Storage
Page 738: Assessment
Page 743: Standardized Test Prep
Page 708: Practice Problems
Page 709: Practice Problems
Page 712: Practice Problems
Page 717: Lesson Check
Page 720: Practice Problems
Page 723: Practice Problems
Page 725: Practice Problems
Page 726: Practice Problems
Page 727: Lesson Check
Page 729: Practice Problems
Page 731: Practice Problems
Page 733: Practice Problems
Page 734: Lesson Check
Chapter 21: Electric Current and Electric Circuits
Section 21.1: Electric Current, Resistance, and Semiconductors
Section 21.2: Electric Circuits
Section 21.3: Power and Energy in Electric Circuits
Page 775: Assessment
Page 781: Standardized Test Prep
Page 747: Practice Problems
Page 751: Practice Problems
Page 757: Lesson Check
Page 759: Practice Problems
Page 762: Practice Problems
Page 763: Practice Problems
Page 765: Lesson Check
Page 766: Practice Problems
Page 769: Practice Problems
Page 771: Lesson Check
Page 771: Practice Problems
Chapter 22: Magnetism and Magnetic Fields
Section 22.1: Magnets and Magnetic Fields
Section 22.2: Magnetism and Electric Currents
Section 22.3: The Magnetic Force
Page 810: Assessment
Page 815: Standardized Test Prep
Page 791: Practice Problems
Page 794: Practice Problems
Page 795: Lesson Check
Page 798: Practice Problems
Page 801: Practice Problems
Page 802: Practice Problems
Page 804: Practice Problems
Page 806: Lesson Check
Chapter 23: Electromagnetic Induction
Section 23.1: Electricity from Magnetism
Section 23.2: Electric Generators and Motors
Section 23.3: AC Circuits and Transformers
Page 844: Assessment
Page 849: Standardized Test Prep
Page 821: Practice Problems
Page 822: Practice Problems
Page 827: Lesson Check
Page 830: Practice Problems
Page 831: Lesson Check
Page 833: Practice Problems
Page 835: Practice Problems
Page 840: Lesson Check
Chapter 24: Quantum Physics
Section 24.1: Quantized Energy and Photons
Section 24.2: Wave-Particle Duality
Section 24.3: The Heisenberg Uncertainty Principle
Page 876: Assessment
Page 881: Standardized Test Prep
Page 854: Practice Problems
Page 857: Practice Problems
Page 858: Practice Problems
Page 859: Practice Problems
Page 861: Practice Problems
Page 862: Practice Problems
Page 863: Lesson Check
Page 865: Practice Problems
Page 867: Lesson Check
Chapter 25: Atomic Physics
Section 25.1: Early Models of the Atom
Section 25.2: Bohr’s Model of the Hydrogen Atom
Section 25.3: The Quantum Physics of Atoms
Page 906: Assessment
Page 909: Standardized Test Prep
Page 890: Practice Problems
Page 891: Practice Problems
Page 893: Practice Problems
Page 896: Lesson Check
Chapter 26: Nuclear Physics
Section 26.1: The Nucleus
Section 26.2: Radioactivity
Section 26.3: Applications of Nuclear Physics
Section 26.4: Fundamental Forces and Elementary Particles
Page 944: Assessment
Page 947: Standardized Test Prep
Page 913: Practice Problems
Page 917: Lesson Check
Page 921: Practice Problems
Page 923: Practice Problems
Page 925: Lesson Check
Page 927: Practice Problems
Page 934: Practice Problems
Page 935: Lesson Check
Chapter 27: Relativity
Section 27.1: The Postulates of Relativity
Section 27.2: The Relativity of Time and Length
Section 27.3: E=mc^2
Section 27.4: General Relativity
Page 972: Assessment
Page 975: Standardized Test Prep
Page 955: Practice Problems
Page 957: Practice Problems
Page 958: Lesson Check
Page 959: Practice Problems
Page 961: Lesson Check
Chapter Appendix B: Appendix B
Section 1: Chapter 1
Section 10: Chapter 10
Section 11: Chapter 11
All Solutions
Page 477: Practice Problems
Exercise 45
Solution 1
Solution 2
Step 1
1 of 3
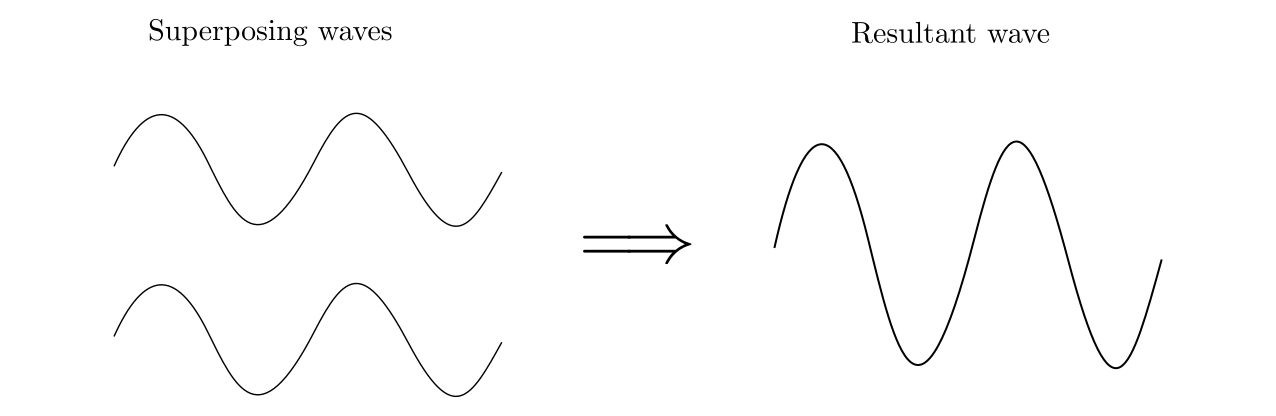
$textbf{(a)}$ The given two waves are having the same phase. Therefore, the resultant wave will have the amplitude as addition of amplitudes of two given waves.
$$
begin{align*}
A_{res} & = A_1 + A_2
end{align*}
$$
The resultant is shown in the given figure.
Step 2
2 of 3
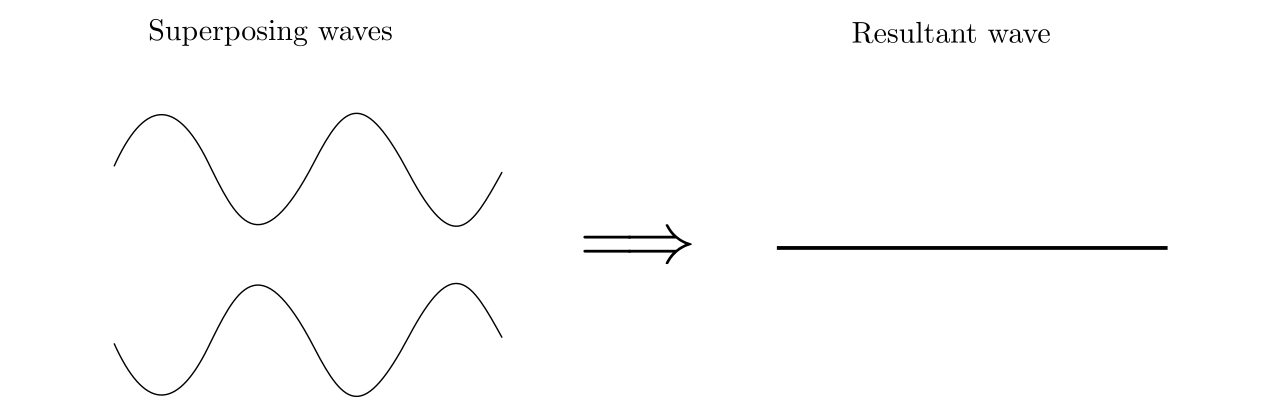
$textbf{(b)}$ The given two waves are having the opposite phase. Let us assume that both the waves have same amplitude. Therefore, the resultant wave will have zero amplitude. waves.
$$
begin{align*}
A_{res} & = A – A = 0
end{align*}
$$
The resultant is shown in the given figure.
Result
3 of 3
The addition of waves are shown in the given figures.
Step 1
1 of 1
In a) the amplitude increases to twice of its initial.
In b) the amplitude falls to zero
(these cases are true only if amplitude in both the graphs are equal)
Exercise 46
Step 1
1 of 6
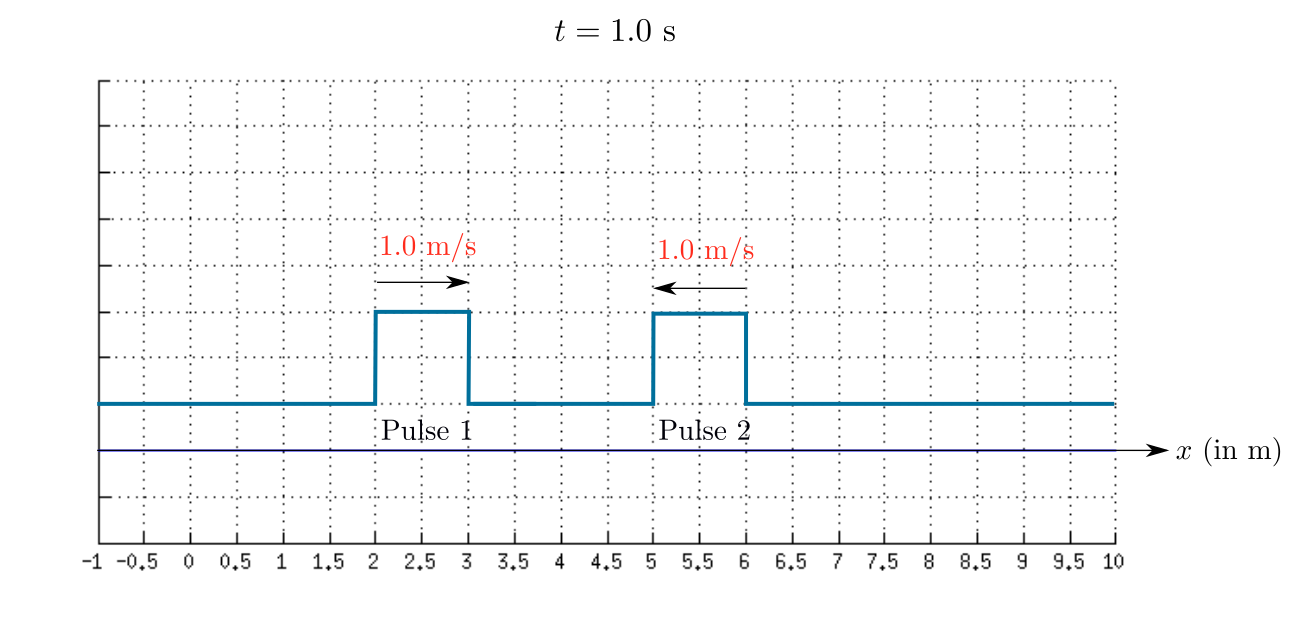
The speed of the first wave and the second wave is given as
$$
begin{align*}
v_1 & = 1.0 mathrm{m/s} \
v_2 & = -1.0 mathrm{m/s}
end{align*}
$$
As time passes the first wave move towards right and the second wave move towards left.
Therefore, the sketch of the resultant wave at $t=1.0$ s is shown in the given figure.
Step 2
2 of 6
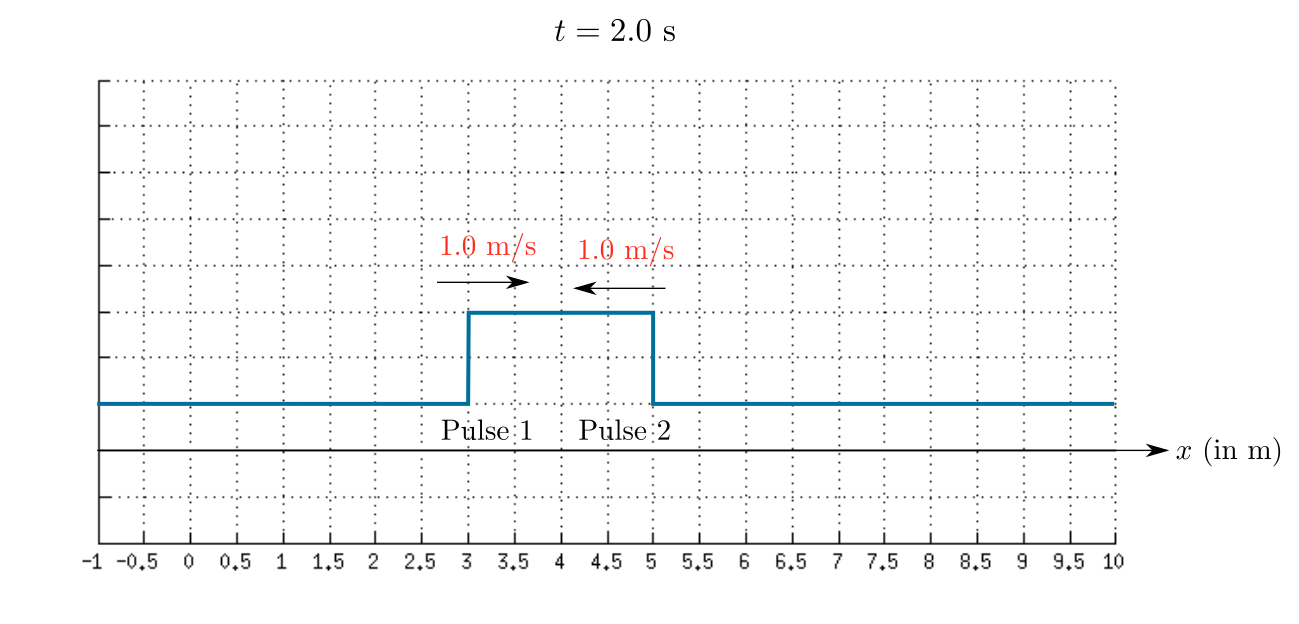
The sketch of the resultant wave at $t=2.0$ s is shown in the given figure.
Step 3
3 of 6
The sketch of the resultant wave at $t=2.5$ s is shown in the given figure.
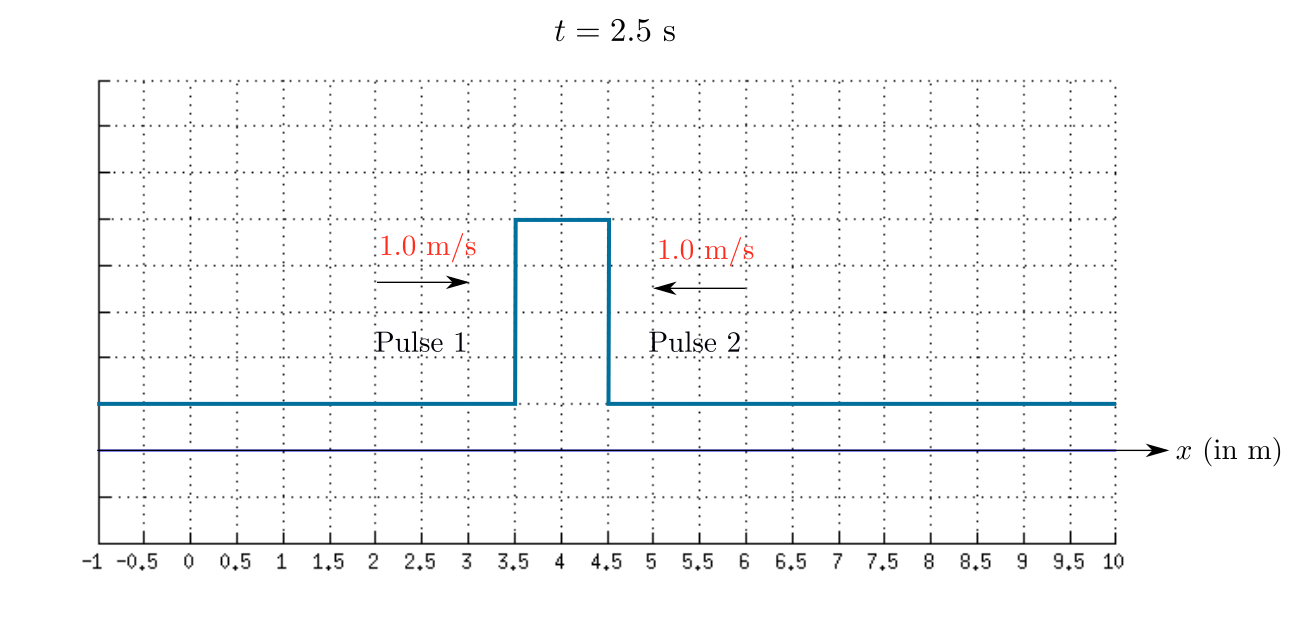
Step 4
4 of 6
The sketch of the resultant wave at $t=3.0$ s is shown in the given figure.
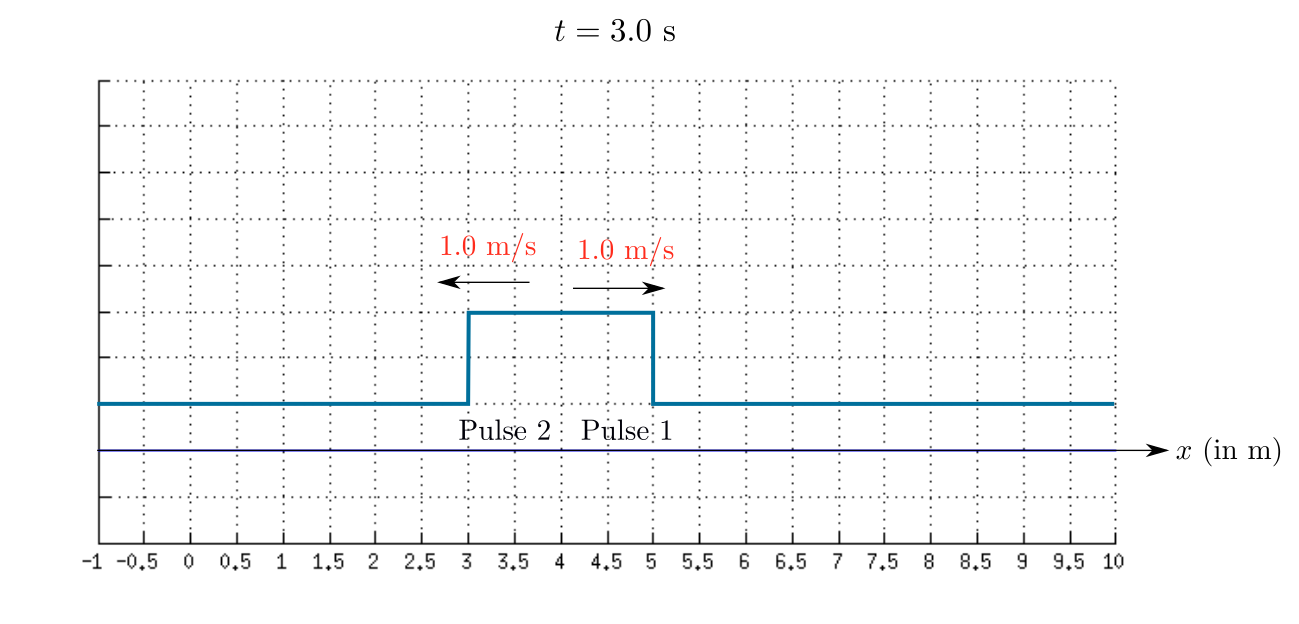
Step 5
5 of 6
The sketch of the resultant wave at $t=4.0$ s is shown in the given figure.
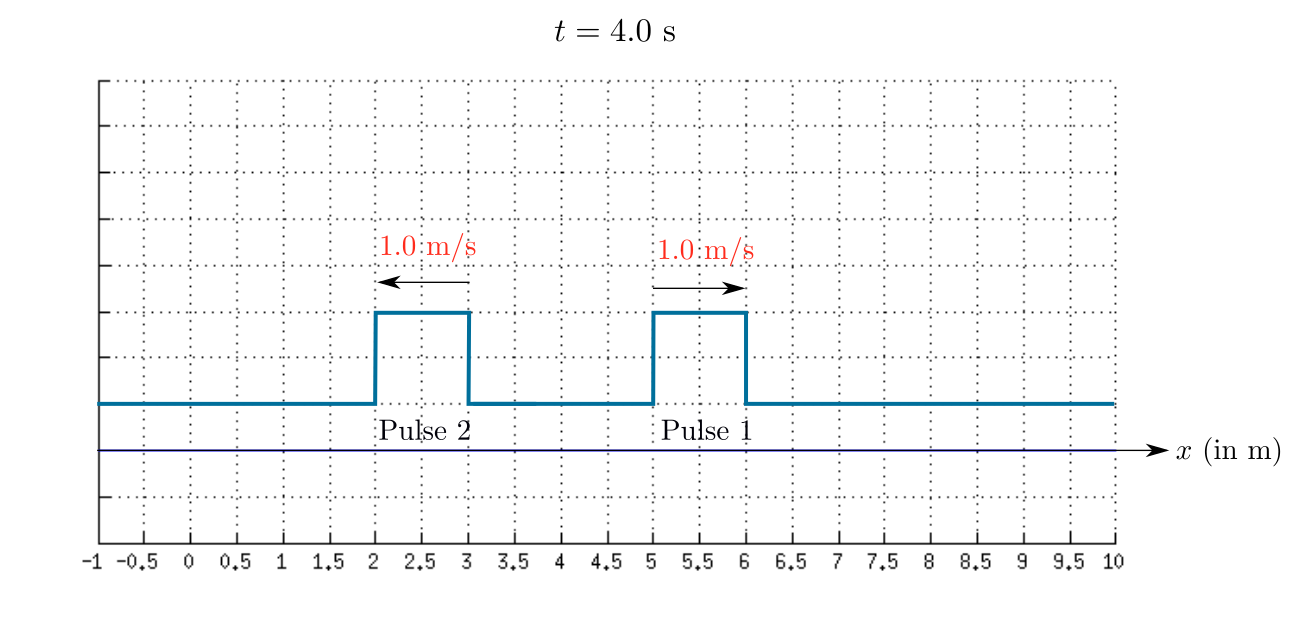
Result
6 of 6
The sketches of the resultant wave are shown in the given figures.
Haven't found what you were looking for?
Search for samples, answers to your questions and flashcards

unlock
