
All Solutions
Page 341: Standardized Test Prep
The Earth’s radius is $R$. The height of the satellite is $r$. The period of the satellite motion is $T$.
$textbf{Required: }$
Finding the orbital speed of the satellite.
In order to evaluate the angular speed of the satellite, we use the following relation:
$$
begin{align*}
omega &= dfrac{v}{r’} \
&= dfrac{ 2 pi }{ T}
end{align*}
$$
Rearrange and solve orbital speed of the satellite:
$$
begin{align*}
v&= dfrac{ 2 pi ~ r’ }{T }\
&= dfrac{ 2 pi ~ left( R + r right) }{T}
end{align*}
$$
So, the answer is “(C) $dfrac{ 2 pi ~ left( R + r right) }{T}$.”
When the skaters lean inward towards the center of the curve, it helps in creating friction between the ice and skater that acts toward the center of the track and provides required centripetal force. So, the answer is “(B) It creates a force between the ice and skates that acts toward the center of the track.”
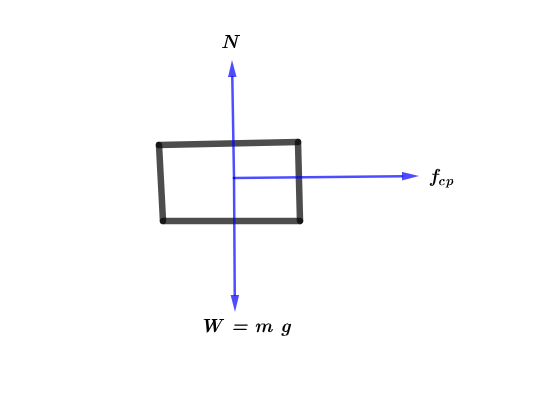
Compare between the FBD in the textbook and the above graph. So, the centripetal force $f_{cp}$ is equals to $B$, the normal force $N$ is equal to $A$, and the weight of the car $W = m g$ is $C$. So, the answer is “(D) $A=N$, $B = f_{cp}$, $C = m ~ g$”.
According to Newton’s second law, the force due to the gravity (Weight) is given by
$$
begin{align*}
F &= W \
&= m_{1} ~ a \
end{align*}
$$
As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ m_{E} }{ r^{2} } \
&= m_{1} ~ a \
&= G ~ dfrac{ m_{1} ~ m_{E} }{ r^{2} } \
end{align*}
$$
Rearrange and solve for the acceleration due to the gravity at the altitude of the International Space Station’s orbit:
$$
begin{align*}
a &= G ~ dfrac{ m_{E} }{ r^{2} } \
end{align*}
$$
So, the gravitational force is inversely proportional to the square of the separation between the space station and Earth. So, if the acceleration due to gravity is lower than the acceleration due to Earth $g$, then the separation between the space station and Earth will decrease. Therefore, the answer is “(B) Orbit farther from Earth, decrease orbital
speed. “
According to Kepler’s second law which assigns that as a planet moves in its orbit, it sweeps out an equal amount of area in an equal amount of time. As we see choices (B) and (D) describe Kepler’s third law. Also, choice (C) describes Kepler’s first law. So, the answer is “(A) the increase in the orbital speed of Earth as it approaches a position closer to the Sun.”
Let the mass of you is $m_{1}$, Earth’s mass is $M_{E}$, and the radius of Earth is $R_{E}$. As Newton’s law of universal gravitation, The force of gravity between two objects is given by
$$
begin{align*}
F &= G ~ dfrac{ m_{1} ~ M_{E} }{ R_{E}^{2} }
end{align*}
$$
As we see the magnitude of the gravitational force depends on the product of the two mass and the separation between you and the center of Earth. According to Newton’s third law:
$$
begin{align*}
vec{F_{E,Y}} &= – vec{F_{Y,E}} \
end{align*}
$$
So, The gravitational force exerted on you by Earth is equal in magnitude to the gravitational force exerted by you on Earth and opposite in the direction. Therefore, the answer is “(C) exactly equal in magnitude to the gravitational
force you exert on Earth.”
Solve for the planet $A$:
As the textbook mentions Kepler’s third law that studied the relation between the distance of a planet from the Star and its orbital period which is given by
$$
begin{align*}
T_{A} &= left( dfrac{ 2 pi }{ sqrt{ G ~ M_{S} } } right) ~ r^{dfrac{3}{2}} \
end{align*}
$$
Similarly, the speed of the satellite that orbiting star is given by
$$
begin{align*}
v_{A} &= sqrt{ dfrac{ G ~ M_{S} }{ R_{A} } }\
end{align*}
$$
Solve for the planet $b$:
As the textbook mentions Kepler’s third law that studied the relation between the distance of a planet from the Star and its orbital period which is given by
$$
begin{align*}
T_{B} &= left( dfrac{ 2 pi }{ sqrt{ G ~ M_{S} } } right) ~ r^{dfrac{3}{2}} \
end{align*}
$$
Similarly, the speed of the satellite that orbiting star is given by
$$
begin{align*}
v_{B} &= sqrt{ dfrac{ G ~ M_{S} }{ R_{B} } }\
&= sqrt{ dfrac{ G ~ M_{S} }{ 4 ~ R_{A} } }\
&= dfrac{1}{2} ~ sqrt{ dfrac{ G ~ M_{S} }{ R_{A} } }\
&= dfrac{1}{2} ~ v_{A} \
end{align*}
$$
As the textbook mentions Kepler’s third law that studied the relation between the distance of a planet from the Star and its orbital period which is given by
$$
begin{align*}
T &= left( dfrac{ 2 pi }{ sqrt{ G ~ M_{S} } } right) ~ r^{dfrac{3}{2}} \
end{align*}
$$
Similarly, the speed of the satellite that orbiting star is given by
$$
begin{align*}
v &= sqrt{ dfrac{ G ~ M_{S} }{ r} }\
end{align*}
$$
So, the orbital speed doesn’t depend on the mass of each planet.
(b) The orbital speed doesn’t depend on the mass of each planet.
Haven't found what you were looking for?
Search for samples, answers to your questions and flashcards

