Home Page Textbooks Physics Page 284: Practice Problems

Physics

1st Edition

Walker

ISBN: 9780133256925

Textbook solutions

All Solutions

Page 284: Practice Problems

Exercise 32

Step 1

1 of 9

(A) $textbf{Graph: }$

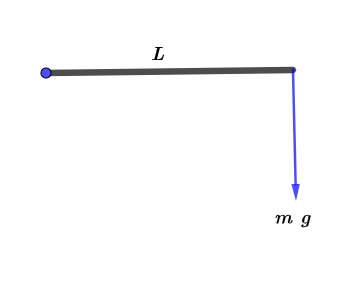
Exercise scan

Step 2

2 of 9

$textbf{Calculation: }$

Solve for the case $A$:

Since the only force that acts on the meterstick is the weight. Then the direction of the net force is downward. As the textbook mentions that the torque is given by the product of force and distance

$$
begin{align*}
tau_{A} &= r ~ F \
&= L ~ m ~ g \
&= mg ~ L
end{align*}
$$

Step 3

3 of 9

(B) $textbf{Graph: }$

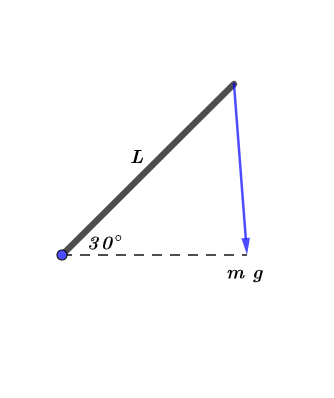
Exercise scan

Step 4

4 of 9

$textbf{Calculation: }$

Solve for the case $B$:

Since the only force that acts on the meterstick is the weight. Then the direction of the net force is downward. As the textbook mentions that the torque is given by the product of force and distance

$$
begin{align*}
tau_{A} &= r ~ F \
&= L ~ m ~ g ~ sin left( theta right) \
&= mg ~ L~ sin left( 60^{circ} right) \
&= dfrac{ sqrt{3} }{2} ~ mg ~ L
end{align*}
$$

Step 5

5 of 9

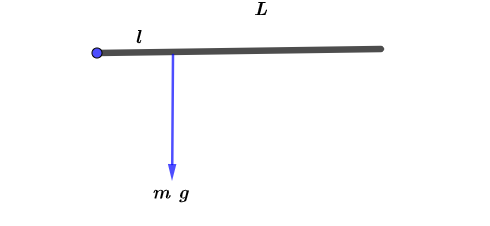
Exercise scan

Step 6

6 of 9

$textbf{Calculation: }$

Solve for the case $C$:

Since the only force that acts on the meterstick is the weight. Then the direction of the net force is downward. As the textbook mentions that the torque is given by the product of force and distance

$$
begin{align*}
tau_{A} &= r ~ F \
&= l ~ m ~ g \
&= mg ~ l
end{align*}
$$

Where, $l<L$.

Step 7

7 of 9

(D) $textbf{Graph: }$

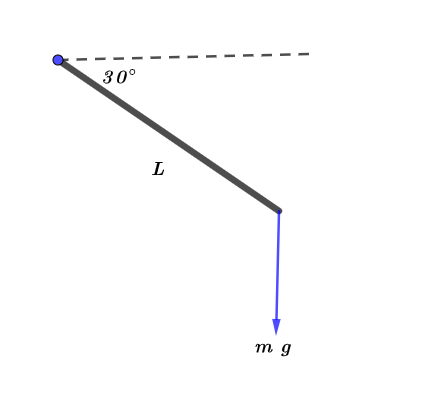
Exercise scan

Step 8

8 of 9

$textbf{Calculation: }$

Solve for the case $D$:

Since the only force that acts on the meterstick is the weight. Then the direction of the net force is downward. As the textbook mentions that the torque is given by the product of force and distance

$$
begin{align*}
tau_{A} &= r ~ F \
&= L ~ m ~ g ~ sin left( theta right) \
&= mg ~ L~ sin left( 60^{circ} right) \
&= dfrac{ sqrt{3} }{2} ~ mg ~ L
end{align*}
$$

Therefore, the order of increasing the difficulty of holding the meterstick still is $C<A<B=D$.

Result

9 of 9

The order of increasing the difficulty of holding the meterstick still is $C<A<B=D$.

Exercise 33

Step 1

1 of 3

$textbf{Given: }$

The wheel’s radius is $r = 0.41 mathrm{~m}$. The force that exerted on the rim of the wheel is $F = 8.8 mathrm{~N}$. The direction that the force makes with the radial direction is $theta = 22^{circ}$.

$textbf{Required: }$

Finding the producing torque by the force.

Step 2

2 of 3

$textbf{Calculation: }$

Since the only force that acts on the meterstick is the weight. Then the direction of the net force is downward. As the textbook mentions that the torque is given by the product of force and distance

$$
begin{align*}
tau &= r ~ F \
&=r ~ F ~ sin left( theta right) \
&= 0.41 mathrm{~m} times 8.8 mathrm{~N} times sin left( 22^{circ} right) \
&= 1.352 mathrm{~N cdot m}
end{align*}
$$

So, the producing torque by the force is $1.352 mathrm{~N cdot m}$.

Result

3 of 3

The producing torque by the force is $1.352 mathrm{~N cdot m}$.

Exercise 34

Step 1

1 of 3

$textbf{Given: }$

$textbf{Required: }$

Finding the maximum producing torque by the force.

Step 2

2 of 3

$textbf{Calculation: }$

Since the only force that acts on the meterstick is the weight. Then the direction of the net force is downward. As the textbook mentions that the torque is given by the product of force and distance

$$
begin{align*}
tau &= r ~ F \
&=r ~ F ~ sin left( theta right) \
&= 0.41 mathrm{~m} times 8.8 mathrm{~N} times sin left( 22^{circ} right) \
&= 1.352 mathrm{~N cdot m}
end{align*}
$$

In order to evaluate the maximum producing torque, the force should be a tangential force. So, the angle $theta$ should be equal to $theta = 90^{circ}$.

Substituting in the previous calculation, then we get

$$
begin{align*}
tau &= r ~ F \
&=r ~ F ~ sin left( theta right) \
&= 0.41 mathrm{~m} times 8.8 mathrm{~N} times sin left( 90^{circ} right) \
&= 3.608 mathrm{~N cdot m}
end{align*}
$$

So, the maximum producing torque by the force is $3.608 mathrm{~N cdot m}$.

Result

3 of 3

The maximum producing torque by the force is $3.608 mathrm{~N cdot m}$.

unlock

All Solutions

Page 284: Practice Problems

Haven't found what you were looking for?

Search for samples, answers to your questions and flashcards