
All Solutions
Page 265: Standardized Test Prep
The mass of the air-track cart is $m = 0.1 mathrm{~kg}$.
Solve for the cart’s momentum:
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
end{align*}
$$
Integrate both sides with the boundary from $0.02 mathrm{~s}$ to $0.12 mathrm{~s}$ (from the graph data):
$$
begin{align*}
int Delta p &= dfrac{1}{2} ~ Int \
&=dfrac{1}{2} ~ int_{0.02}^{0.12} F ~ Delta t \
&= dfrac{1}{2} ~ F ~ int_{0.02}^{0.12} Delta t \
&= dfrac{1}{2} ~ F ~ left( 0.12 mathrm{~s} – 0.02 mathrm{~s} right) \
&= dfrac{1}{2} times 0.5 mathrm{~N} times left( 0.12 mathrm{~s} – 0.02 mathrm{~s} right) \
&= 0.025 mathrm{~kg cdot m/s}
end{align*}
$$
So, the answer is “(B) $0.025 mathrm{~kg cdot m/s}$”.
The mass of the air-track cart is $m = 0.1 mathrm{~kg}$.
Solve for the cart’s momentum:
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
end{align*}
$$
Integrate both sides with the boundary from $0.02 mathrm{~s}$ to $0.12 mathrm{~s}$ (from the graph data):
$$
begin{align*}
int Delta p &= dfrac{1}{2} ~ Int \
&=dfrac{1}{2} ~ int_{0.02}^{0.12} F ~ Delta t \
&= dfrac{1}{2} ~ F ~ int_{0.02}^{0.12} Delta t \
&= dfrac{1}{2} ~ F ~ left( 0.12 mathrm{~s} – 0.02 mathrm{~s} right) \
&= dfrac{1}{2} times 0.5 mathrm{~N} times left( 0.12 mathrm{~s} – 0.02 mathrm{~s} right) \
&= 0.025 mathrm{~kg cdot m/s}
end{align*}
$$
Rearrange and solve for the change in velocity of the cart:
$$
begin{align*}
Delta v &= dfrac{ Delta p }{ m} \
&= dfrac{ 0.025 mathrm{~kg cdot m/s} }{ 0.1 mathrm{~kg} }\
&= 0.25 mathrm{~m/s}
end{align*}
$$
So, the answer is “(D) $0.25 mathrm{~m/s}$”.
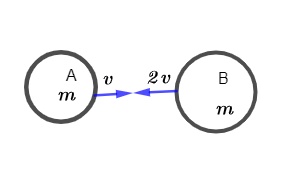
Solve for the final speed of the object $A$ is equal to $v_{f,2} = 2 v$ to the left:
According to conservation law of momentum, the impulse is equal to zero.
$$
begin{align*}
Delta p_{t} &= Delta p_{1} + Delta p_{2} \
&= 0 \
&= m_{1} ~ left( vec{v_{f,1}} – vec{v_{i,1}} right) + m_{2} ~ left( vec{v_{f,2}} – vec{v_{i,2}} right) \
&= m ~ left( vec{v_{f,1}} – vec{v_{i,1}} right) + m ~ left( vec{v_{f,2}} – vec{v_{i,2}} right) \
&= left( vec{v_{f,1}} – vec{v_{i,1}} right) + left( vec{v_{f,2}} – vec{v_{i,2}} right) \
&= left( 2 v – v right) + left( vec{v_{f,2}} – 2 v right) \
&= vec{v_{f,2}} – v
end{align*}
$$
So, the final velocity of the object $B$ after the collision is “(D) $v$ to the right”.
Solve for inelastic collision:
If the total external force that affecting the system is zero, then the system obeys the conservation law of momentum. So, the initial momentum of the system is equal to the final momentum of the system. Therefore, in the elastic collision (ideal state), the initial kinetic energy is equal to the final kinetic energy. In the real world, there are no ideal cases. So, in the real world, there is some energy lost in the inelastic collision. But we know that the energy is conservative. Energy is neither destroyed nor created but changes from to another. So, the lost energy in the inelastic collision is transformed into some other forms of energy as thermal, sound, and friction.
So, the answer is “(A) kinetic energy is changed to other forms of energy”.
As the textbook mentions that the initial momentum of the ball is given by the mass times the velocity.
$$
begin{align*}
Delta vec{p} &= m ~ Delta vec{v} \
end{align*}
$$
Rearrange and solve for the change in velocity:
$$
begin{align*}
Delta vec{v} &= dfrac{ Delta vec{p} }{ m } \
end{align*}
$$
So, the answer is “(D) $dfrac{ Delta p }{m}$”.
The mass of the first cart is $m_{1} = 1 mathrm{~kg}$. The initial velocity of first cart is $v_{i,1} = 2 mathrm{~m/s}$ to the right. The mass of the second cart is $m_{2} = 2 mathrm{~kg}$. The initial velocity of the second cart $v_{i,2} = 3 mathrm{~m/s}$ to the left. The final velocity of first cart is $v_{f,1} = 2 mathrm{~m/s}$ to the left.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
According to conservation law of momentum, the impulse is equal to zero.
$$
begin{align*}
Delta p_{t} &= Delta p_{1} + Delta p_{2} \
&= 0 \
&= m_{1} ~ left( vec{v_{f,1}} – vec{v_{i,1}} right) + m_{2} ~ left( vec{v_{f,2}} – vec{v_{i,2}} right) \
&= m_{1} ~ left( vec{v_{f,1}} – 0right) + m_{2} ~ left( vec{v_{f,2}} – 0 right) \
&= 1 mathrm{~kg}~ left( 2 mathrm{~m/s} – left( – 2 mathrm{~m/s} right) right) + 2 mathrm{~kg} ~ left( vec{v_{f,2}} – 3 mathrm{~m/s} right) \
&= 4 mathrm{~kg cdot m/s} + 2 ~ vec{v_{f,2}} – 6 mathrm{~kg cdot m/s} \
&= 2 mathrm{~kg} ~ vec{v_{f,2}} – 2 mathrm{~kg cdot m/s} \
end{align*}
$$
Rearrange and solve for the final velocity of the second cart:
$$
begin{align*}
v_{f,2} &= dfrac{ 2 mathrm{~kg cdot m/s} }{ 2 mathrm{~kg} } \
&= 1 mathrm{ m/s} \
end{align*}
$$
So, the final velocity of the second cart is $1 mathrm{~m/s}$ toward the right. Therefore, the answer is “(B) $1 mathrm{~m/s}$ toward the right “.
According to the Momentum-Impulse Theorem:
$$
begin{align*}
vec{I} &= vec{F} ~ Delta t \
&= Delta vec{p} \
&= left( vec{p_{f}} – vec{p_{i}} right) \
&= left( m ~ vec{v_{f}} – m ~ vec{v_{i}} right) \
&= m ~ left( vec{v_{f}} – vec{v_{i}} right) \
end{align*}
$$
According to conservation law of momentum, the impulse is equal to zero.
$$
begin{align*}
Delta p_{t} &= Delta p_{1} + Delta p_{2} \
&= 0 \
&= m_{1} ~ left( vec{v_{f,1}} – vec{v_{i,1}} right) + m_{2} ~ left( vec{v_{f,2}} – vec{v_{i,2}} right) \
end{align*}
$$
Let the bus and the bowling ball will be in contact after the collision. Substituting in the previous calculations, then we get
$$
begin{align*}
m_{1} ~ left( vec{v_{f}} – vec{v_{i,1}} right) + m_{2} ~ left( vec{v_{f}} – vec{v_{i,2}} right) &= 0 \
&= m_{1} ~ vec{v_{f}} + m_{2} ~ vec{v_{f}} – left( _{1} ~ vec{v_{i,1}} – m_{2} ~ vec{v_{i,2}} right) \
end{align*}
$$
Rearrange and solve for the final speed of the bus and the ball:
$$
begin{align*}
vec{v_{f}} &= dfrac{ left( _{1} ~ vec{v_{i,1}} – m_{2} ~ vec{v_{i,2}} right) }{ m_{1} + m_{2} } \
end{align*}
$$
So, the final speed of the bus should be decreased after the collision.
Haven't found what you were looking for?
Search for samples, answers to your questions and flashcards

