${large textbf{Knowns}}$

The maximum static friction on an object is proportional to the normal force on the object:

$$
begin{gather*}
f_{s,max} = mu_s N tag{1}
end{gather*}
$$

Where the proportionality constant is the coefficient of static friction between the object and the surface.

${large textbf{Givens}}$

The coefficient of static friction between the pumpkin and the table is $mu_s = 0.55$ and the mass of the pumpkin is $m = 1.80$ kg.

${large textbf{Calculations}}$

(a) As in Guided Example 5.12, the pumpkin starts to move when the weight of the pail (with the sand in it) equals the maximum static friction on the pumpkin.

From equation (1), the maximum static friction is proportional to the coefficient of static friction for constant normal force;

So if the coefficient is decreased from $0.61$ to $0.55$ the maximum static friction decreases and so the weight of the pile required is $textbf{less than $11.0$ N}$

(b) Since the pumpkin has no acceleration in the vertical direction, we apply $textbf{Newton’s first law}$ to the pumpkin in the $y$ direction, so we get:

$$
begin{align*}
sum F_y = N – w &= 0\\
N & = w = mg
end{align*}
$$

Now, we plug our value for $m$, so we get the normal force on the pumpkin:

$$
begin{gather*}
N = (1.80text{ kg})cdot(9.81text{ m/s}^2) = 17.7text{ N}
end{gather*}
$$

Then, we plug our values for $N$ and $mu_s$ into equation (1), so we get the maximum static friction on the pumpkin:

$$
begin{gather*}
f_{s,max} = (0.550)cdot(17.7text{ N}) = 9.71text{ N}
end{gather*}
$$

In the horizontal direction, there are two forces acting on the pumpkin, the weight of the pile to the right and the static friction force to the left.

At the moment when the pumpkin starts to move (still no acceleration), the static friction is maximum;

So, we apply $textbf{Newton’s first law}$ to the pumpkin in the $x$ direction, so we get:

$$
begin{align*}
sum F_x = f_{s,max} – w_text{pail} &= 0\\
w_{text{pail}} & = f_{s,max}
end{align*}
$$

Thus, the required weight of the pail is:

$$
begin{gather*}
large boxed{w_text{pail} = 9.71text{ N}}
end{gather*}
$$

(a) $textbf{Less than 11 N}$.

(b) $w_text{pail} = 9.71$ N

${large textbf{Knowns}}$

The maximum static friction on an object is proportional to the normal force on the object:

$$
begin{gather*}
f_{s,max} = mu_s Ntag{1}
end{gather*}
$$

The kinetic friction on an object is proportional to the normal force on the object:

$$
begin{gather*}
f_k = mu_k Ntag{2}
end{gather*}
$$

Where $mu_s$ is the coefficient of static friction and $mu_k$ is the coefficient of kinetic friction.

${large textbf{Givens}}$

The mass of the book is $m = 1.80$ kg, the force required to set the book in motion is $F_{s} = 2.25$ N and the force required to keep the book in motion with constant speed is $F_k = 1.50$ N.

${large textbf{Calculations}}$

When the book was at rest, there is no acceleration in any direction.

In the vertical direction, there are two forces acting on the book, one is its weight directed downward and the other is the normal force exerted by the table directed upward.

So, we apply $textbf{Newton’s first law}$ to the book in the $y$ direction, so we get:

$$
begin{align*}
sum F_y = N – w &= 0\\
N &= w = mg
end{align*}
$$

Now, we plug our value for $m$, so we get the normal force on the book:

$$
begin{gather*}
N = (1.80text{ kg}) cdot (9.81text{ m/s}^2) = 17.7text{ N}
end{gather*}
$$

In the horizontal direction, there are two forces acting on the book, one is the applied force and the other is the static friction force which is equal in magnitude and opposite in direction to the applied force.

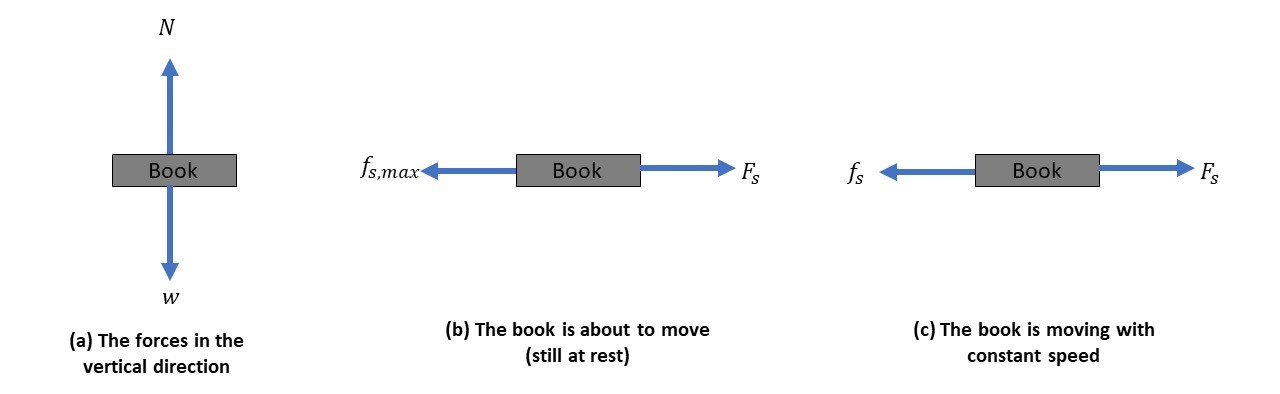
At the moment when the book is about to move, the static friction is maximum.

So, we apply $textbf{Newton’s first law}$ to the book in the $x$ direction at this moment, so we get:

$$
begin{align*}
sum F_x = F_s – f_{s,max} &= 0\\
f_{s,max} &= F_s = 2.25text{ N}
end{align*}
$$

Now, we plug our values for $f_{s,max}$ and $N$ into equation (1) and evaluate for $mu_s$, so we get the coefficient of static friction between the book and the tabletop:

$$
begin{gather*}
mu_s = dfrac{f_{s,max}}{N} = dfrac{2.25text{ N}}{17.7text{ N}} = 0.127\\
therefore quad large boxed{mu_s = 0.127}
end{gather*}
$$