
All Solutions
Page 169: Lesson Check
Each force is represented by an arrow with its tail attached to the object and its head is directed in the same direction of the force.
Also, if possible, we try to adjust its length to indicates the magnitude of the force.
– We choose a coordinate system, for example, upward as the $+y$-direction and the right is the $+x$-direction.
– We resolve each force into components.
– We apply $textbf{Newton’s law}$ to the object in each direction.
– Finally, we solve the equation for the required quantity.
W=mg , where g is the acceleration due to gravity.
Example: an object placed on a table at rest will have its gravitational weight acting downwards and the normal force by the table acting on it upwards.
So the distance of stretch is directly proportional to the force exerted by the spring.
$$
begin{gather*}
large boxed{x propto F}
end{gather*}
$$
And the constant of the proportionality is $1/k$.
x propto F
$$
$$
begin{align*}
T &= dfrac{mg}{2sin{theta}}\\
Rightarrow sin{theta} & = dfrac{mg}{2T}
end{align*}
$$
Where $theta$ is the agle of the sag.
So, without changing anything else, increasing the tension in the clothesline decreases the quantity $sin{theta}$ and so the angle $theta$ decreases.
Therefore, it is necessary to $textbf{increase}$ the tension in the clothesline in order to decrease the angle of the sag.
The mass of the child is $m_1 = 9.30$ kg and the mass of the chair is $m_2 = 3.70$ kg.
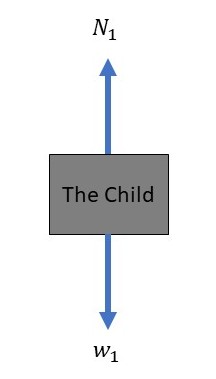
There are two forces acting on the child, one is gravitational force (weight) directed downward and the other one is the normal force exerted by the chair which is directed upward.
Since the child is at rest, we apply $textbf{Newton’s first law}$ to the child in the $y$-direction, so we get:
$$
begin{align*}
sum F_y = N_1 – w_1 &= 0\\
N_1 &= w_1 = m_1 g\\
& = (9.30text{ kg})cdot(9.81text{ m/s}^2) = 91.2text{ N}
end{align*}
$$
$$
therefore quad large boxed{N_1 = 91.2text{ N}}
$$
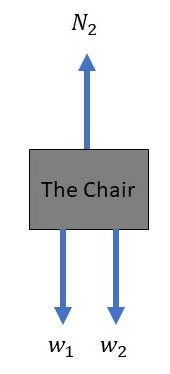
There are three forces acting on the chair, one is the gravitational force (its weight) directed downward, the second force is the normal force exerted by the child which equals the child’s weight and it is directed downward, and the last force is the normal force exerted by the ground which is directed upward.
Since the chair is at rest, we apply $textbf{Newton’s first law}$ to the chair in the $y$-direction, so we get:
$$
begin{align*}
sum F_y = N_2 – w_1 – w_2 & = 0\\
N_2 &= w_1 + w_2\\
& = (m_1 + m_2) g\\
& = (9.30text{ kg} + 3.70text{ kg})cdot (9.81text{ m/s}^2) = 128text{ N}
end{align*}
$$
$$
therefore quad large boxed{N_2 = 128text{ N}}
$$
$textbf{Note}$: the normal force exerted by the child on the chair is the reaction force to the normal force exerted by the chair on the child, and from part (a), we found that the normal force on the child equals her weight;
So, according to $textbf{Newton’s third law}$, the force exerted by the child on the chair is also equal to the weight of the child.
(b) $N_2 = 128$ N
From $textbf{Hook’s law}$, the force exerted by an ideal spring of constant $k$ is proportional to the distance of its stretch or compression $x$:
$$
begin{gather*}
F = kxtag{1}
end{gather*}
$$
The spring constant of the spring is $k = 62.0$ N/m and the distance of stretch is $x = 19.0$ cm.
The applied force equals in magnitude ad opposite in direction to the force exerted by the spring.
So, we simply plug our values for $k$ and $x$ into equation (1), so we get the magnitude of the applied force :
$$
begin{gather*}
F = (62.0text{ N/m})cdot (0.190text{ m}) = \\
therefore quad large boxed{F = 11.8text{ N}}
end{gather*}
$$
From $textbf{Newton’s second law}$ for multiple forces, the net force acting on an object is equal to its mas times its acceleration:
$$
begin{gather*}
sum vec{textbf{F}} = mvec{textbf{a}}tag{1}
end{gather*}
$$
The magnitude of the force exerted by the first astronaut is $F_1 = 42.0$ N and the angle of the net force on the satellite is $theta = 15.0text{textdegree}$ with respect to $+x$-axis.
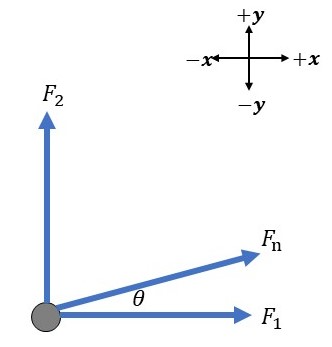
The figure below shows a $textbf{free-body diagram}$ of the satellite.
First, we resolve the three forces in the diagram into their components.
For the force exerted by the first astronaut, it is directed in the $+x$-direction, so
$$
begin{align*}
F_{1x} &= F_1 \\
F_{1y} & = 0
end{align*}
$$
For the force exerted by the second astronaut, it is directed in the $+y$-direction, so
$$
begin{align*}
F_{2x} &= 0\\
F_{2y} & = F_2
end{align*}
$$
For the net force, it makes an angle $theta$ with the $+x$-axis, so
$$
begin{align*}
F_{nx} &= F_n cos{theta}\\
F_{ny} & = F_n sin{theta}
end{align*}
$$
$$
begin{align*}
sum F_x = F_{nx} &= F_{1x} + F_{2x}\\
F_{n} cos{theta} & = F_1\\
F_n & = dfrac{F_1}{cos{theta}}
end{align*}
$$
Now, we plug our values for $F_1$ and $theta$, so we get the magnitude of the net force on the satellite:
$$
begin{gather*}
F_n = dfrac{42.0text{ N}}{cos{15.0}} = 43.5text{ N}
end{gather*}
$$
Then, we apply $textbf{Newton’s second law}$ to the satellite in the $y$-direction, so we get:
$$
begin{align*}
sum F_y = F_{ny} &= F_{1y} + F_{2y}\\
F_{n} sin{theta} & = F_2\\
F_2 & = F_n sin{theta}
end{align*}
$$
Now, we plug our values for $F_n$ and $theta$, so we get the magnitude of the force exerted by the second astronaut on the satellite:
$$
begin{gather*}
F_2 = ( 43.5text{ N}) sin{15.0} = 11.3text{ N}\\
therefore quad large boxed{F_2 = 11.3text{ N}}
end{gather*}
$$
Haven't found what you were looking for?
Search for samples, answers to your questions and flashcards

