Home Page Textbooks Physics Page 149: Standardized Test Prep

Physics

1st Edition

Walker

ISBN: 9780133256925

Textbook solutions

All Solutions

Page 149: Standardized Test Prep

Exercise 1

Step 1

1 of 2

From the first graph,the maximum altitude or vertical displacement is $45:m$.

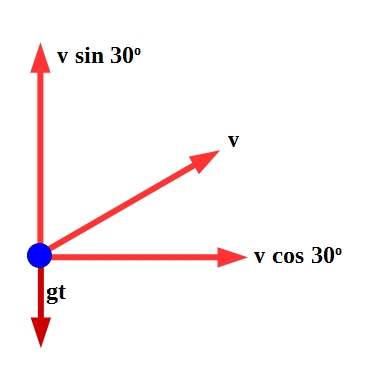
This is the point at which the vertical velocity becomes zero.

Result

2 of 2

(D) 45 m

Exercise 2

Step 1

1 of 2

Various components of velocity of the projectile during its flight is shown below.

$v cos 30^o$ is the horizontal component. From the diagram,

$v sin 30^o$ and $gt$ are vertical components but they are opposite to each other.

So the vertical velocity of the projectile is $v sin 30^o – gt$.

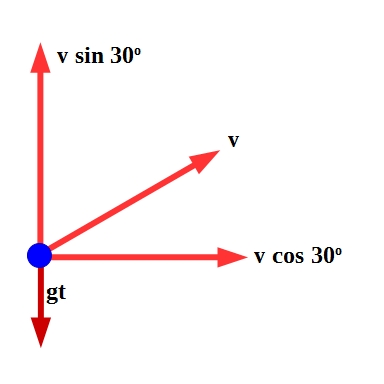
Exercise scan

Result

2 of 2

(A) $v sin 30^o -gt$

Exercise 3

Step 1

1 of 2

Velocity components of the projectile during its flight is shown below.

From the diagram, $v cos 30^o$ is the horizontal component of the velocity.

Exercise scan

Result

2 of 2

(B) $v cos 30^o$

Exercise 4

Step 1

1 of 3

constant acceleration in one dimension and
constant velocity in the other dimension.

Step 2

2 of 3

in projectile motion we have same horizontal velocity and constant acceleration in vertical direction which results parabolic path

Result

3 of 3

Exercise 5

Step 1

1 of 2

we have 2 velocity orthogonal to each other so their magnitude will be $sqrt {(200 km / h) ^2 + (70 km / h)^2}$

Result

2 of 2

Exercise 6

Step 1

1 of 2

when we travelling in one direction we can see that all still objects have a speed equal to us in opposite direction

Result

2 of 2

Exercise 7

Step 1

1 of 4

$newcommand{tx}$[1]${text{#1}}$

#### Known

To add two vectors, we place the tail of the second vector on the head of the first vector. The resultant vector is the vector that goes from the tail of the first to the head of the second. Always keeping the directions of the vectors and their lengths.

Therefore, the result is option (C).

We can see this in the following figure:

Step 2

2 of 4

Step 3

3 of 4

With:

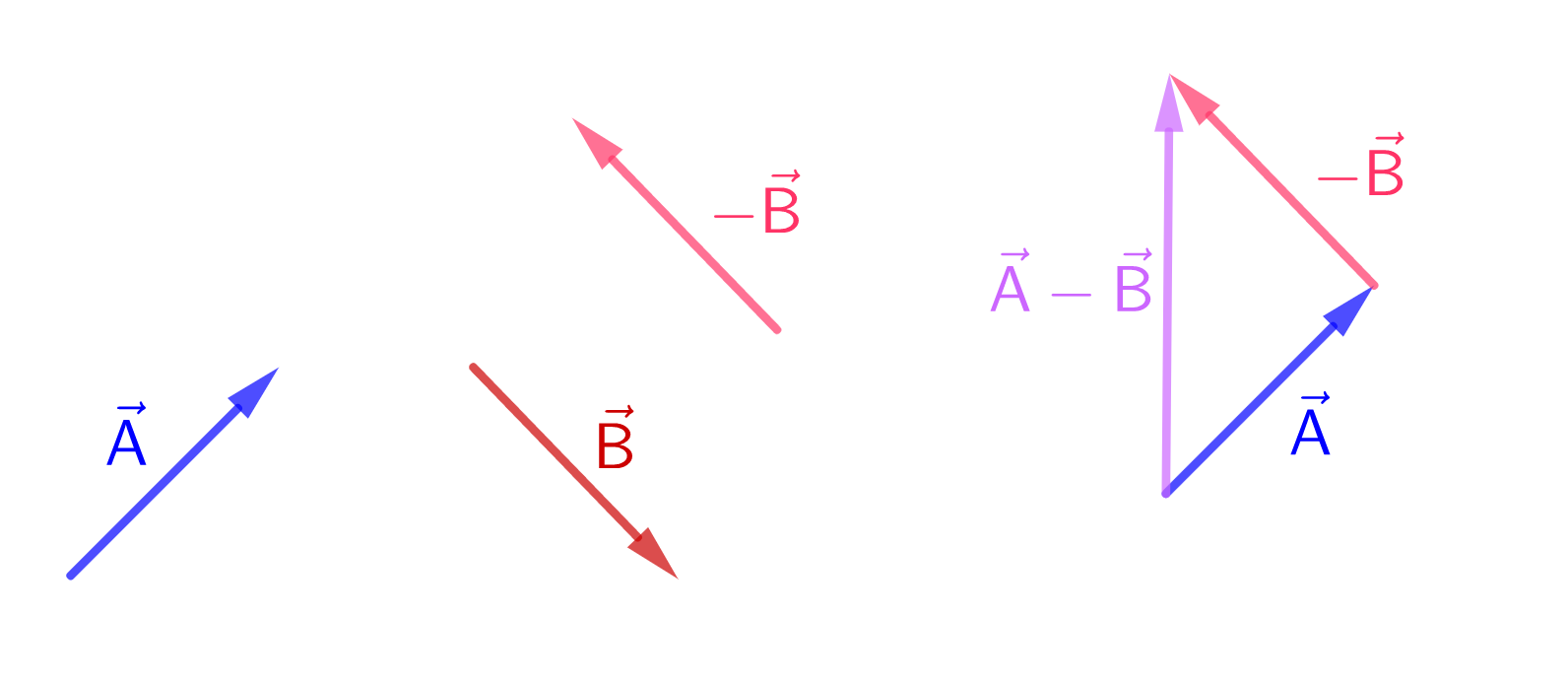
$$
begin{align*}
vec{A}-vec{B}=vec{A}+(-vec{B})
end{align*}
$$

—

#### Conclusion

Option (C).

Result

4 of 4

Option (C).

Exercise 8

Step 1

1 of 2

$newcommand{tx}$[1]${text{#1}}$

#### Known

The vertical position of a projectile can be determined with one of the following equations:

$$
begin{align}
y_f&=y_i+v_{y,i}cdot t-frac{gcdot t^2}{2}\
v_{y,f}^2&=v_{y,i}^2-2g(y_f-y_i)
end{align}
$$

From the position time graph, we have:

The time position graph gives us precisely the information of which is the vertical position (position on the $y$ axis) of the projectile for each instant of time. Therefore, from the graph we can see directly that for $t=4 tx{s}$ the height of the projectile is $40 tx{m}$. In the same way we can determine the vertical position for any other instant of time.

From the velocity time graph we can know what is the velocity (vertical) of the projectile at $t=4 tx{s}$ and also for $t=0 tx{s}$ what is its initial velocity (vertical). With this information and using equation (2), we can calculate the vertical position of the projectile at $t=4 tx{s}$.

From (2) we have:

$$
begin{align*}
y_f-y_i=frac{v_{y,f}^2-v_{y,i}^2}{-2g}
end{align*}
$$

With $v_i=30 frac{tx{m}}{tx{s}}$ at $t=0 tx{s}$. $v_f=-10 frac{tx{m}}{tx{s}}$ at $t=4 tx{s}$. $y_i=0 tx{m}$. $gapprox 10 frac{tx{m}}{tx{s}^2}$.

Therefore:

$$
begin{align*}
y_f-0 tx{m}&=frac{left(-10 frac{tx{m}}{tx{s}}right)^2-left(30 frac{tx{m}}{tx{s}}right)^2}{-2left(10 frac{tx{m}}{tx{s}^2}right)}\
y_f&=40 tx{m}
end{align*}
$$

This is the same result that is observed in the position-time graph.

—

#### Conclusion

The vertical position of the projectile can be determined directly from the position-time graph. With the velocity-time graph we need the equations of motion to determine the vertical position of the projectile.

Result

2 of 2

unlock

All Solutions

Page 149: Standardized Test Prep

Haven't found what you were looking for?

Search for samples, answers to your questions and flashcards