
All Solutions
Page 140: Lesson Check
#### Known
The expressions of the $x$ and $y$ components of the positions of a projectile are given by:
$$
begin{align*}
&x_f=x_i+left(v_i tx{cos} thetaright)t\
&y_f=y_i+left(v_i tx{sin} thetaright)t+frac{a_ycdot t^2}{2}, tx{with} a_y=-g=-9.81 frac{tx{m}}{tx{s}^2}
end{align*}
$$
The previous expressions constitute the parametric equation of a parabola, considering the time $t$ as a parameter. That is, the combined motion of a projectile on the $x$-axis and on the $y$-axis gives a parabolic trajectory.
This can be seen easily, if the $y$ component is solved in terms of the $x$ component, that is, isolate the parameter $t$ in one of the expressions and replace it in the other expression.
—
#### Conclusion
The trajectory that a projectile describes is a parabola.
#### Known
$$
begin{align*}
R=left(frac{v_i^2}{g}right) tx{sin}(2theta), tx{Range equation}
end{align*}
$$
Where $theta$ is the launch angle with respect to the $x$ axis.
#### Calculation
Therefore, for given an initial velocity $v_i$ and a value of gravity $g$, the range will only depend on the launch angle $theta$.
The above implies that the maximum launch range will be obtained when:
$$
begin{align*}
tx{sin}(2theta)=1implies theta=frac{pi}{4}=45^circ, tx{for} 0<theta<90^circ
end{align*}
$$
—
#### Conclusion
Therefore, we have:
$$
begin{align*}
boxed{R_{tx{max}}=frac{v_i^2}{g}}
end{align*}
$$
begin{align*}
boxed{R_{text{max}}=frac{v_i^2}{g}}
end{align*}
$$
#### Known
Considering the acceleration of gravity $g$ downwards and with constant magnitude and taking into account that for a projectile (the thrown ball and the dropped ball) the horizontal and vertical movements are independent. We come to the conclusion that the acceleration is both cases is the same.
—
#### Conclusion
The acceleration in both cases is the same.
#### Known
The components of the initial velocity $vec{v}_i$ of a projectile launched at an angle $theta$ with respect to the horizontal, are given by:
$$
begin{align}
v_{x,i}=v_i tx{cos}(theta)hspace{0.5cm}tx{and}hspace{0.5cm}v_{y,i}=v_i tx{sin}(theta)
end{align}
$$
Flight time is the time for the projectile to fall since it was launched. In the case that the projectile falls to the same horizontal height as where it was launched, this time is given by:
$$
begin{align}
t_v=frac{2v_i tx{sin}(theta)}{g}
end{align}
$$
Therefore, from figure 4.30, we have:
For the same initial speed in all cases.
a) The projectile $C$ has the largest horizontal component of initial velocity (see expression (1)). Since it is the one with the smallest launch angle $theta$ and therefore the value of $tx{cos}(theta)$ is greater than the rest.
Therefore, projectile $A$ has the smallest horizontal component of initial velocity, followed by projectile $B$ and the largest for projectile $C$.
b) From the figure, it can be seen that projectile $A$ takes more time in the air (flight time), since it reaches a higher height that the rest. This, taking into account that the vertical movement of a projectile is independent of its horizontal movement (no matter how large its initial horizontal velocity is).
Therefore, projectile $C$ has the smallest time of flight, followed by $B$ and the longest flight time for projectile $A$. This can also be seen from expression (2).
—
#### Conclusion
$$
begin{align*}
tx{a}) boxed{A<B<C}hspace{1cm} tx{b}) boxed{C<B<A}
end{align*}
$$
begin{align*}
text{a}) boxed{A<B<C}hspace{1cm} text{b}) boxed{C<B<A}
end{align*}
$$
#### Known
Range equation.
$$
begin{align*}
R=left(frac{v_i^2}{g}right) tx{sin}(2theta)
end{align*}
$$
Where $theta$ is the launch angle with respect to the $x$ axis. Therefore:
$$
begin{align}
R_{tx{max}}=frac{v_i^2}{g}, tx{for} theta=45^circ
end{align}
$$
#### Calculation
Givens: From Example 4.12: $v_i=13.5 frac{tx{m}}{tx{s}}$, $g=9.81 frac{tx{m}}{tx{s}^2}$.
From (1) we have:
$$
begin{align*}
R_{tx{max}}=frac{left(13.5 frac{tx{m}}{tx{s}}right)^2}{9.81 frac{tx{m}}{tx{s}^2}}=18.59 tx{m}
end{align*}
$$
—
#### Conclusion
If the golf ball was thrown at an angle of $45^circ$ to the horizontal, it would travel a horizontal distance of $18.59 tx{m}$.
boxed{R_{text{max}}=18.59 text{m}}
$$
$$
begin{align*}
v_text{y, f} &= v_text{y, i} – gt \
implies t &= frac{v_text{y, i} – v_text{y, f}}{g} \
&= frac{8.2~mathrm{m/s} – 0}{9.81~mathrm{s}} \
&= 0.83588~mathrm{s} \
t &= boxed{ 0.84~mathrm{s} }
end{align*}
$$
t = 0.84~mathrm{s}
$$
#### Known
The horizontal and vertical position ($x, y$) of a projectile as a function of time are given by:
$$
begin{align}
&x_f=x_i+left(v_i tx{cos} thetaright)t\
&y_f=y_i+left(v_i tx{sin} thetaright)t+frac{a_ycdot t^2}{2}, a_y=-g
end{align}
$$
#### Calculation
Givens: $v_i=18 frac{tx{m}}{tx{s}}$, $theta=35^circ$, $x_i=0 tx{m}$, $y_i=0 tx{m}$, $g=9.81 frac{tx{m}}{tx{s}^2}$
From (1) and (2) we have:
a) At $t=0.5 tx{s}$
$$
begin{align*}
&x=x_f=0 tx{m}+left(18 frac{tx{m}}{tx{s}}cdot tx{cos}(35^circ)right)(0.5 tx{s})=7.37 tx{m}\
&y=y_f=0 tx{m}+left(18 frac{tx{m}}{tx{s}}cdot tx{sin}(35^circ)right)(0.5 tx{s})-frac{left(9.81 frac{tx{m}}{tx{s}^2}right)(0.5 tx{s})^2}{2}=3.94 tx{m}
end{align*}
$$
At $t=1.0 tx{s}$
$$
begin{align*}
&x=x_f=0 tx{m}+left(18 frac{tx{m}}{tx{s}}cdot tx{cos}(35^circ)right)(1.0 tx{s})=14.74 tx{m}\
&y=y_f=0 tx{m}+left(18 frac{tx{m}}{tx{s}}cdot tx{sin}(35^circ)right)(1.0 tx{s})-frac{left(9.81 frac{tx{m}}{tx{s}^2}right)(1.0 tx{s})^2}{2}=5.42 tx{m}
end{align*}
$$
At $t=1.5 tx{s}$
$$
begin{align*}
&x=x_f=0 tx{m}+left(18 frac{tx{m}}{tx{s}}cdot tx{cos}(35^circ)right)(1.5 tx{s})=22.12 tx{m}\
&y=y_f=0 tx{m}+left(18 frac{tx{m}}{tx{s}}cdot tx{sin}(35^circ)right)(1.5 tx{s})-frac{left(9.81 frac{tx{m}}{tx{s}^2}right)(1.5 tx{s})^2}{2}=4.45 tx{m}
end{align*}
$$
At $t=2.0 tx{s}$
$$
begin{align*}
&x=x_f=0 tx{m}+left(18 frac{tx{m}}{tx{s}}cdot tx{cos}(35^circ)right)(2.0 tx{s})=29.49 tx{m}\
&y=y_f=0 tx{m}+left(18 frac{tx{m}}{tx{s}}cdot tx{sin}(35^circ)right)(2.0 tx{s})-frac{left(9.81 frac{tx{m}}{tx{s}^2}right)(2.0 tx{s})^2}{2}=1.03 tx{m}
end{align*}
$$
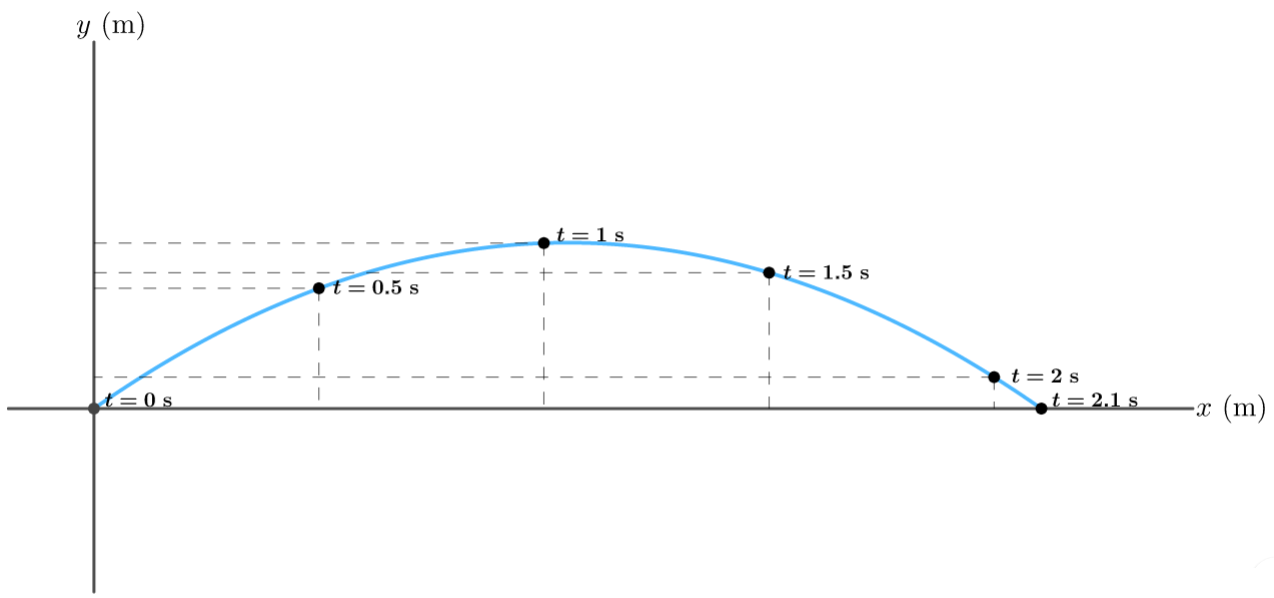
b) The figure:
#### Conclusion
a) At $0.5 tx{s}$, $x=7.37 tx{m}$ and $y=3.94 tx{m}$. At $1.0 tx{s}$, $x=14.74 tx{m}$ and $y=5.42 tx{m}$. At $1.5 tx{s}$, $x=22.12 tx{m}$ and $y=4.45 tx{m}$. At $2.0 tx{s}$, $x=29.49 tx{m}$ and $y=1.03 tx{m}$.
#### Known
For a vector $vec{v}$ with $v_x$ and $v_y$, the speed $v$ (magnitude $vec{v}$) is given by:
$$
begin{align}
v=sqrt{v^2_x+v^2_y}
end{align}
$$
#### Calculation
Givens: $v_{x,i}=v_{x,f}=1.85 frac{tx{m}}{tx{s}}$, because the motion of a projectile on the $x$ axis is independent of the motion on the $y$ axis. $v_f=0 tx{m}$, $y_i=3 tx{m}$, $v_{y,i}=0 frac{tx{m}}{tx{s}}$, $g=9.81 frac{tx{m}}{tx{s}^2}$.
Calculating the $y$ component of the velocity at the instant before entering the water.
$$
begin{align*}
v^2_{y,f}&=v^2_{y,i}+2a_yleft(y_f-y_iright), tx{with} a_y=-g\
&=left(0 frac{tx{m}}{tx{s}}right)^2-2left(9.81 frac{tx{m}}{tx{s}^2}right)left(0 tx{m}-3 tx{m}right)\
v^2_{y,f}&=58.86 frac{tx{m}^2}{tx{s}^2}implies v_{y,f}=-7.67 frac{tx{m}}{tx{s}},
end{align*}
$$
Considering the downward direction as negative.
Therefore, from (1) we have:
$$
begin{align*}
&v=sqrt{(v_{x,f})^2+(v_{y,f})^2}=sqrt{left(1.85 frac{tx{m}}{tx{s}}right)^2 +left(-7.67 frac{tx{m}}{tx{s}}right)^2}\
&boxed{v=7.89 frac{tx{m}}{tx{s}}}
end{align*}
$$
—
#### Conclusion
The divers speed is $7.89 frac{tx{m}}{tx{s}}$.

