#### Known

A vector $vec{C}$ with components $C_x$ and $C_y$ has a magnitude (size of the vector) of:

$$
begin{align}
C=sqrt{C_x^2+C_y^2}
end{align}
$$

#### Calculation

Givens: $v_{x,f}=12.0 frac{tx{m}}{tx{s}}$, $v_{y,f}=-9.81 frac{tx{m}}{tx{s}}$, at the time $1.00 tx{s}$.

From (1) we have:

$$
begin{align*}
v_f&=sqrt{v^2_{x,f}+v^2_{y,f}}\
&=sqrt{left(12.0 frac{tx{m}}{tx{s}}right)^2+left(-9.81 frac{tx{m}}{tx{s}}right)^2}=15.50 frac{tx{m}}{tx{s}}
end{align*}
$$

$$
begin{align*}
boxed{v_f=15.50 frac{tx{m}}{tx{s}}}
end{align*}
$$

—

#### Conclusion

$$
begin{align*}
boxed{v=15.50 frac{tx{m}}{tx{s}}}
end{align*}
$$

#### Known
.

A vector $vec{C}$ with components $C_x$ and $C_y$ has a direction of:

$$
begin{align}
theta=tx{tan}^{-1}left(frac{C_y}{C_x}right)
end{align}
$$

#### Calculation

Givens: $v_{x,f}=12.0 frac{tx{m}}{tx{s}}$, $v_{y,f}=-9.81 frac{tx{m}}{tx{s}}$. At the time $1.00 tx{s}$

From (1) we have:

$$
begin{align*}
theta&=tx{tan}^{-1}left(frac{v_{y,f}}{v_{x,f}}right)\
&=tx{tan}^{-1}left(frac{-9.81 frac{tx{m}}{tx{s}}}{12.0 frac{tx{m}}{tx{s}}}right)=-39.3^circ
end{align*}
$$

$$
begin{align*}
boxed{theta=-39.3^circ}
end{align*}
$$

—

#### Conclusion

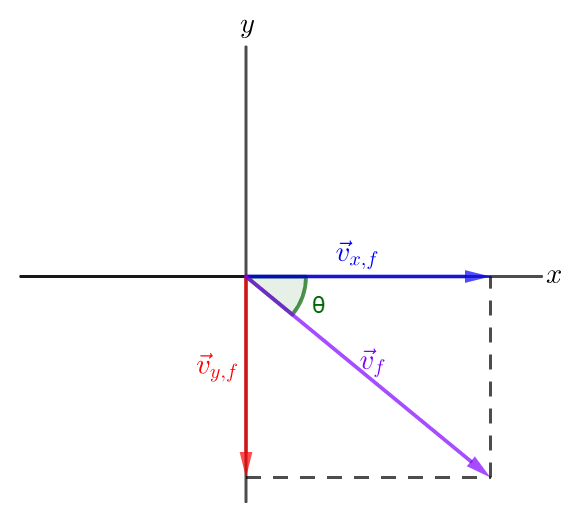
The direction of velocity is $-39.3^circ$ with respect to the positive $x$ axis or $39.3^circ$ below the positive $x$ axis.

Graphically: