
All Solutions
Page 127: Practice Problems
#### Known
Taking into account that the position of a vector is not relevant, we can add two or more vectors moving them parallel to the point where we want to add it to another vector. That is, moving the vectors while maintaining the direction they have. For example:
In Figure 1 we have a vector $vec{A}$ and a vector $vec{B}$. If we want to add $vec{A}+vec{B}$, we move vector $vec{B}$ keeping its direction until we put the tail of $vec{B}$ on the head of $vec{A}$. Then the resulting vector is the vector that goes from the tail of $vec{A}$ to the head of $vec{B}$. If we want to calculate the sum $vec{B}+vec{A}$ we do the same as in the previous case, but now we translate vector $vec{A}$, we see that the result will be the same even though the resulting vectors are in different positions. Figure 2.
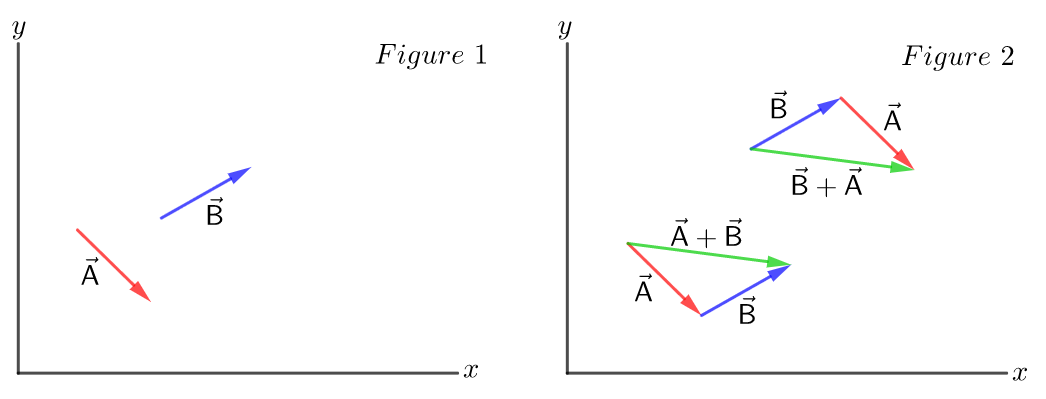
—
#### Conclusion
We can add two or more vectors moving them parallel to the point where we want to add it to another vector. That is, moving the vectors while maintaining the direction they have.
#### Known
The vector resulting from adding two or more vectors has as the $x$ component, the sum of all the $x$ components of the vectors in the sum, as the $y$ component, the sum of all the $y$ components of the vectors in the sum. If we have more coordinates besides $x$ and $y$, the method is the same.
For example, if we have:
$$
begin{align*}
vec{A}=left(A_x, A_y, A_zright), vec{B}=left(B_x, B_y, B_zright) tx{and} vec{C}=left(C_x, C_y, C_zright)
end{align*}
$$
The sum $vec{D}=vec{A}+vec{B}+vec{C}$, has a components:
$$
begin{align*}
&D_x=A_x+B_x+C_x\
&D_y=A_x+B_y+C_y\
&D_z=A_z+B_z+C_z
end{align*}
$$
With:
$$
begin{align*}
boxed{vec{D}=left(D_x, D_y, D_zright)}
end{align*}
$$
—
#### Conclusion
The vector resulting from adding two or more vectors has as the $x$ component, the sum of all the $x$ components of the vectors in the sum, as the $y$ component, the sum of all the $y$ components of the vectors in the sum. If we have more coordinates besides $x$ and $y$, the method is the same.
#### Known
The location of a vector does not matter.
Vectors $vec{A}$, $vec{D}$ and $vec{E}$ are shown in Figure 1. The sums $vec{K}=vec{A}+vec{D}$ and $vec{L}=vec{A}+vec{E}$ are shown in Figure 2.
From Figure 2 we can see that the length (magnitude) of $vec{K}$ is greater than the length of $vec{L}$, taking into account that $vec{D}$ and $vec{E}$ have the same length.
We can also see this analytically using the law of cosines. Where:
$$
begin{align*}
K^2=A^2+D^2-2AD tx{cos}(theta)
end{align*}
$$
And
$$
begin{align*}
L^2=A^2+E^2-2AE tx{cos}(phi)
end{align*}
$$
With $0<phi<90^circ$ and $90^circ<theta<180^circ$.
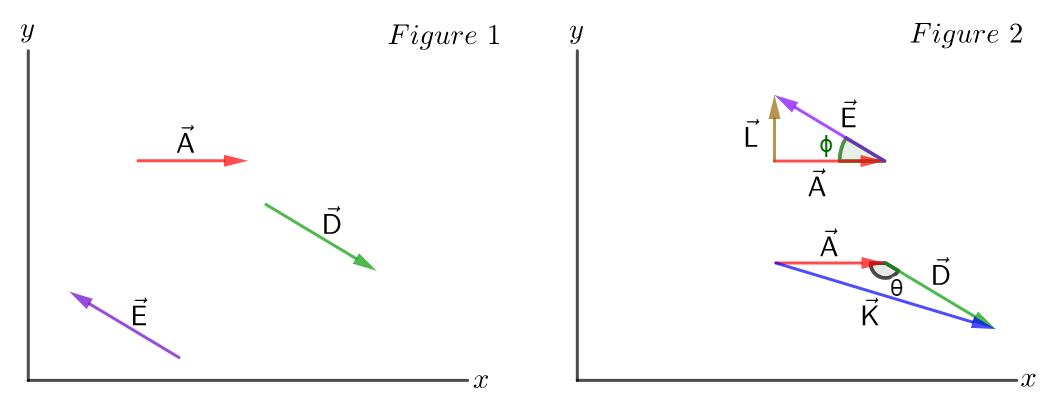
$$
begin{align*}
boxed{L<K}
end{align*}
$$
—
#### Conclusion
The magnitude of $vec{K}=vec{A}+vec{D}$ is greater than the magnitude of $vec{L}=vec{A}+vec{E}$.
#### Known
The location of a vector does not matter.
Vectors $vec{B}$, $vec{C}$, $vec{F}$, $-vec{C}$ and $-vec{F}$ are shown in Figure 1. The subtractions $vec{P}=vec{B}-vec{C}$ and $vec{Q}=vec{B}-vec{F}$ are shown in Figure 2.
From Figure 2 we can see that the length (magnitude) of $vec{Q}$ is greater than the length of $vec{P}$, taking into account that $vec{C}$ and $vec{F}$ have the same length.
We can also see this analytically using the law of cosines. Where:
$$
begin{align*}
P^2=B^2+C^2-2BC tx{cos}(phi)
end{align*}
$$
And
$$
begin{align*}
Q^2=B^2+F^2-2BF tx{cos}(theta)
end{align*}
$$
With $0<phi<90^circ$ and $90^circ<theta<180^circ$.
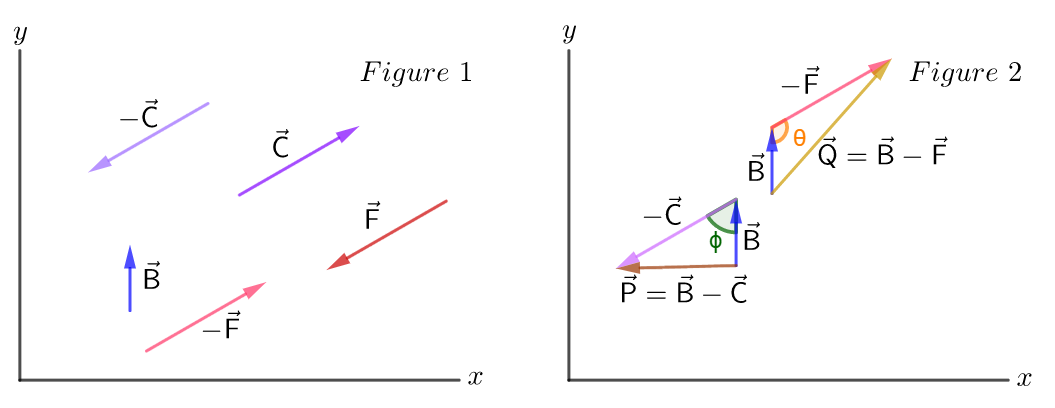
$$
begin{align*}
boxed{P<Q}
end{align*}
$$
—
#### Conclusion
The magnitude of $vec{P}=vec{B}-vec{C}$ is less than the magnitude $vec{Q}=vec{B}-vec{F}$.
#### Known
A vector length (magnitude) and direction. The position of the vector is not relevant.
#### Calculation
Figure 1 shown vectors $vec{A}$ and $vec{B}$ of the problem.
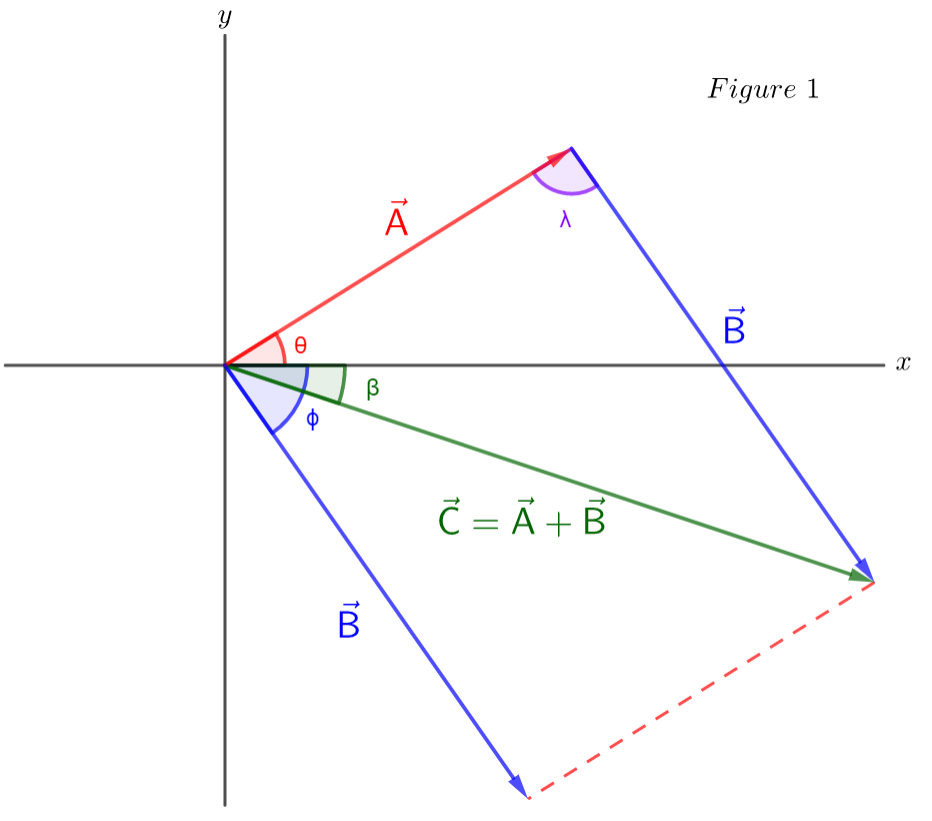
From the figure, we can see that the angle that $vec{C}$ makes below the positive $x$-axis is approximately equal to a little less than half of $55^circ$. Also from the figure we can infer that the magnitude of $vec{C}$ is a little less than double the value of the magnitude of $vec{A}$, $27 tx{m}$. That is, $vec{C}$ points approximately in a direction $22^circ$ below the positive $x$-axis and has a magnitude of approximately $48 tx{m}$.
An exact result can be reached either using the component method or geometry (law of cosines and law of sines, etc).
—
#### Conclusion
$vec{C}$ points approximately in a direction $22^circ$ below the positive $x$-axis and has a magnitude of approximately $48 tx{m}$.
#### Known
The sum of two vector is equal to a vector whose components is the sum of the respective components of the two vectors. This is:
$$
begin{align}
vec{C}=vec{A}+vec{B}implies C_x=A_x+B_x tx{and} C_y=A_y+B_y
end{align}
$$
#### Calculation
Givens: $A=27 tx{m}$ with $theta=32^circ$ above the positive $x$ axis. $B=35 tx{m}$ with $phi=55^circ$ below the positive $x$ axis.
Calculating the components of $vec{A}$ and $vec{B}$.
$$
begin{align*}
&A_x=A tx{cos}(theta)=(27 tx{m}) tx{cos}(32^circ)=22.9 tx{m}approx 23 tx{m}\
&A_y=A tx{sin}(theta)=(27 tx{m}) tx{sin}(32^circ)=14.3 tx{m}approx 14 tx{m}\
&B_x=B tx{cos}(phi)=(35 tx{m}) tx{cos}(55^circ)=20.1 tx{m}approx 20 tx{m}\
&B_y=-B tx{sin}(phi)=(-35 tx{m}) tx{sin}(55^circ)=-28.7 tx{m}approx -29 tx{m}\
end{align*}
$$
The negative sign of the $y$ component of $vec{B}$ is due to the fact that $vec{B}$ has a direction of $55^circ$ below the $x$-axis, therefore its $y$ component is on the negative axis of the $y$-axis.
From (1) we have:
$$
begin{align*}
&C_x=22.9 tx{m}+20.1 tx{m}=43 tx{m}\
&C_y=14.3 tx{m}-28.7 tx{m}=-14.4 tx{m}approx -14 tx{m}\
&implies vec{C}=left(C_x, C_yright)=(43 tx{m}, -14 tx{m})
end{align*}
$$
The magnitude and direction of $vec{C}$ can be calculated as:
$$
begin{align*}
C=sqrt{C^2_x+C^2_y}=sqrt{(43 tx{m})^2+(-14.4 tx{m})^2}=45.3 tx{m}approx 45 tx{m}
end{align*}
$$
$$
begin{align*}
theta&=tx{tan}^{-1}left(frac{C_y}{C_x}right)=tx{tan}^{-1}left(frac{-14.4 tx{m}}{43 tx{m}}right)\
&=-18.5^circapprox-19^circ tx{or} 19^circ tx{below the} x-tx{axis}.
end{align*}
$$
—
#### Conclusion
Vector $vec{C}$ has a magnitude of $45 tx{m}$ and point in a direction $19^circ$ below the positive $x$ axis.
.
#### Known
The magnitude and direction of a vector $vec{A}=left(A_x, A_yright)$ are determined by:
$$
begin{align*}
A=sqrt{A^2_x+A^2_y} tx{and} theta=tx{tan}^{-1}left(frac{A_y}{A_x}right)
end{align*}
$$
#### Calculation
Givens: $A=12 tx{m}$ and points in the positive direction of the $y$-axis. $B=33 tx{m}$ and points in the negative direction of the $x$-axis.
Since the position of a vector is not relevant, only the magnitude and its direction matter. We can place vectors $vec{A}$ and $vec{B}$ as shown in the figure, this for convenience.
From the figure, we can see that:
$$
begin{align*}
&vec{A}=left(A_x, A_yright)=(0, 12 tx{m})\
&vec{B}=left(B_x, B_yright)=(-33 tx{m}, 0)
end{align*}
$$
Therefore:
a)
$$
begin{align*}
vec{C}=vec{A}+vec{B}
end{align*}
$$
With:
$$
begin{align*}
&C_x=A_x+B_x=0 tx{m}-33 tx{m}=-33 tx{m}\
&C_y=A_y+B_y=12 tx{m}+0 tx{m}=12 tx{m}\
&implies vec{C}=left(C_x, C_yright)=(-33 tx{m}, 12 tx{m})\
&implies C=sqrt{(-33 tx{m})^2+(12 tx{m})^2}=35 tx{m}
end{align*}
$$
And
$$
begin{align*}
theta=tx{tan}^{-1}left(frac{12 tx{m}}{-33 tx{m}}right)=&160^circ tx{above the positive} x-tx{axis or} 20^circ tx{above the negative} xtx{axis}.
end{align*}
$$
Other vector directions can also be specified.
We will use:
$theta=20^circ$ above the negative $x$ axis.
b)
$$
begin{align*}
vec{D}=vec{A}-vec{B}
end{align*}
$$
With:
$$
begin{align*}
&D_x=A_x-B_x=0 tx{m}-(-33 tx{m})=33 tx{m}\
&D_y=A_y-B_y=12 tx{m}-0 tx{m}=12 tx{m}\
&implies vec{D}=left(D_x, D_yright)=(33 tx{m}, 12 tx{m})\
&implies D=sqrt{(33 tx{m})^2+(12 tx{m})^2}=35 tx{m}
end{align*}
$$
And
$$
begin{align*}
theta=tx{tan}^{-1}left(frac{12 tx{m}}{33 tx{m}}right)=&20^circ tx{above the positive} x tx{axis}
end{align*}
$$
c)
$$
begin{align*}
vec{F}=vec{B}-vec{A}
end{align*}
$$
With:
$$
begin{align*}
&F_x=B_x-A_x=-33 tx{m}-0 tx{m}=-33 tx{m}\
&F_y=B_y-A_y=0 tx{m}-12 tx{m}=-12 tx{m}\
&implies vec{F}=left(F_x, F_yright)=(-33 tx{m}, -12 tx{m})\
&implies F=sqrt{(-33 tx{m})^2+(-12 tx{m})^2}=35 tx{m}
end{align*}
$$
And
$$
begin{align*}
theta=tx{tan}^{-1}left(frac{-12 tx{m}}{-33 tx{m}}right)=&20^circ tx{below the negative} x-tx{axis}
end{align*}
$$
Note that:
$$
begin{align*}
tx{tan}^{-1}left(frac{12 tx{m}}{33 tx{m}}right)neq tx{tan}^{-1}left(frac{-12 tx{m}}{-33 tx{m}}right)
end{align*}
$$
The first is in the first quadrant and the second is in the third quadrant.
—
#### Conclusion
a) $vec{C}=vec{A}+vec{B}$ has magnitude of $35 tx{m}$ and points in a direction $20^circ$ above the negative $x$ axis.
b) $vec{D}=vec{A}-vec{B}$ has magnitude of $35 tx{m}$ and points in a direction $20^circ$ above the positive $x$ axis.
c) $vec{F}=vec{B}-vec{A}$ has magnitude of $35 tx{m}$ and points in a direction $20^circ$ below the negative $x$ axis.
The following figures show each of the cases.
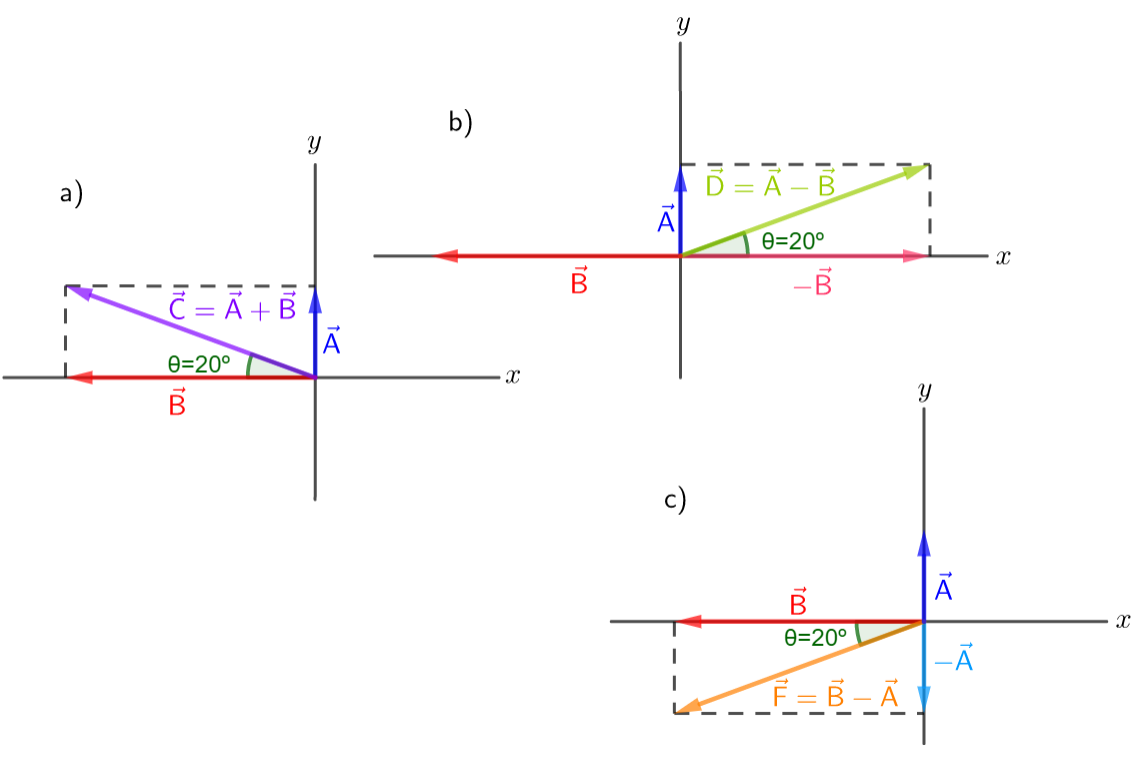
b) $vec{D}=vec{A}-vec{B}$ has magnitude of $35 text{m}$ and points in a direction $20^circ$ above the positive $x$ axis.
c) $vec{F}=vec{B}-vec{A}$ has magnitude of $35 text{m}$ and points in a direction $20^circ$ below the negative $x$ axis.

