$newcommand{tx}$[1]${text{#1}}$

#### Known

The location of a vector does not matter.

Also:

$$
begin{align}
vec{A}-vec{B}=vec{A}+(-vec{B})
end{align}
$$

Where $-vec{B}$ has the same length as vector $vec{B}$, but with the opposite direction.
#### Calculation

Givens: Figure 4.16.

a) Vectors $vec{A}$, $vec{B}$ and $-vec{B}$ are shown in Figure 1. The subtraction $vec{D}=vec{A}-vec{B}$ is shown in Figure 2.

b) Vectors $vec{A}$, $vec{D}$, $vec{E}$, $-vec{D}$ and $-vec{E}$ are shown in Figure 3. The subtractions $vec{H}=vec{A}-vec{D}$ and $vec{G}=vec{A}-vec{E}$ are shown in Figure 4.

$newcommand{tx}$[1]${text{#1}}$
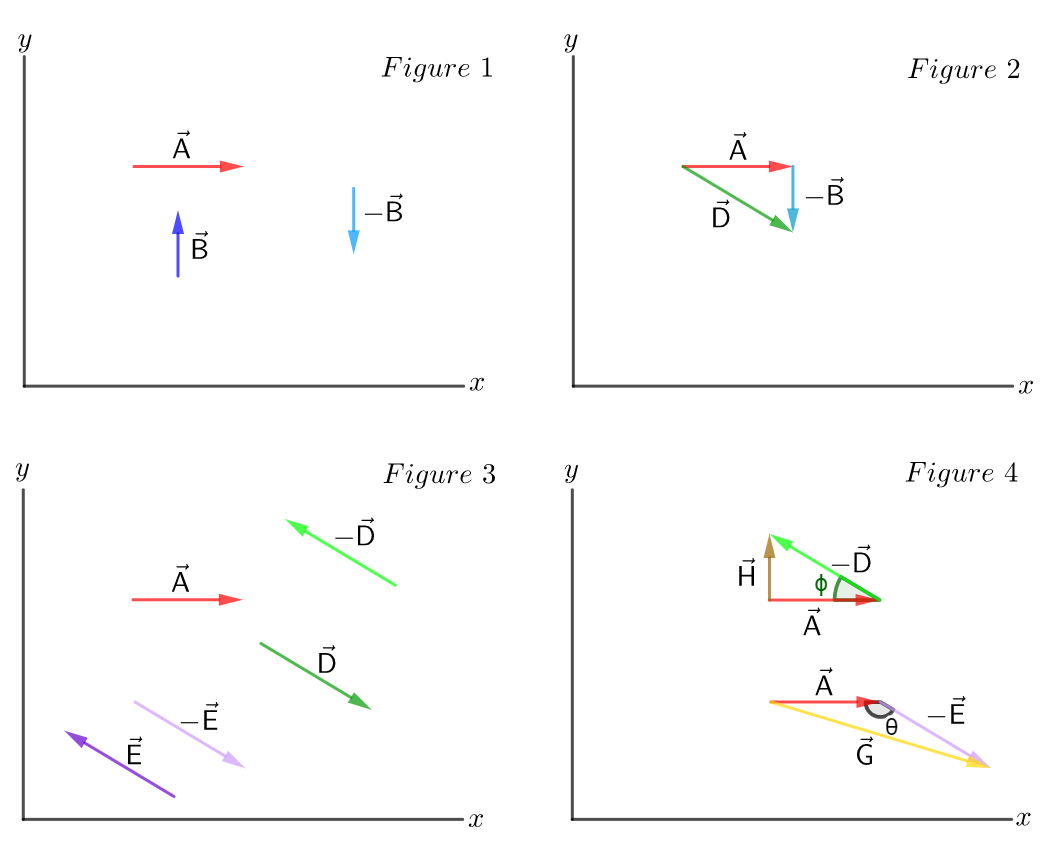
From Figure 4 we can see that the length (magnitude) of $vec{G}$ is greater than the length of $vec{H}$, taking into account that $vec{D}$ and $vec{E}$ have the same length.

We can also see this analytically using the law of cosines. Where:

$$
begin{align*}
H^2=A^2+D^2-2AD tx{cos}(phi)
end{align*}
$$

And

$$
begin{align*}
G^2=A^2+E^2-2AE tx{cos}(theta)
end{align*}
$$

With $0<phi<90^circ$ and $90^circ<theta<180^circ$.

Therefore:

$$
begin{align*}
boxed{H<G}
end{align*}
$$

—

#### Conclusion

This is, the magnitude of $vec{H}=vec{A}-vec{D}$ is less than the magnitude $vec{G}=vec{A}-vec{E}$.

The magnitude of $vec{H}=vec{A}-vec{D}$ is less than the magnitude $vec{G}=vec{A}-vec{E}$.