Home Page Textbooks Physics Page 120: Lesson Check

Physics

1st Edition

Walker

ISBN: 9780133256925

Textbook solutions

All Solutions

Page 120: Lesson Check

Exercise 10

Step 1

1 of 2

$newcommand{tx}$[1]${text{#1}}$

#### Known

A scalar is fully described with a number.

A vector is fully described with a number (its length) and a direction.

Therefore:

The difference is that vectors have direction.

Note that units of measurement are not essential to define a scalar or a vector.

—

#### Conclusion

The difference is that vectors have direction.

Result

2 of 2

The difference is that vectors have direction.

Exercise 11

Step 1

1 of 2

$newcommand{tx}$[1]${text{#1}}$

#### Known

The magnitude of a vector refers to its length, while the direction refers to its orientation.

—

#### Conclusion

The magnitude of a vector refers to its length.

Result

2 of 2

The magnitude of a vector refers to its length.

Exercise 12

Step 1

1 of 3

$newcommand{tx}$[1]${text{#1}}$

#### Known

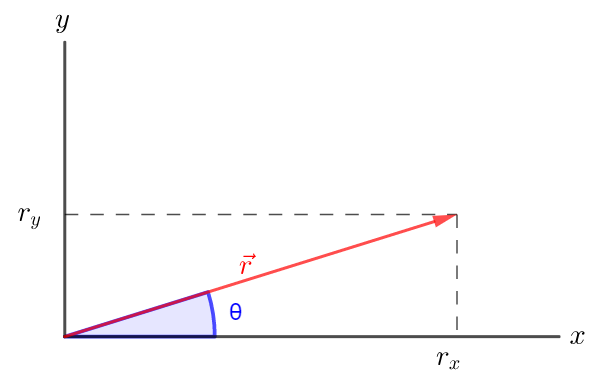
Defining the magnitude of a vector $vec{r}$ as $r$, we have:

$$
begin{align*}
r=sqrt{r^2_x+r^2_y} (tx{Pythagorean theorem.})
end{align*}
$$

Where $r_x$ is the $x$ component and $r_y$ is the $y$ component of the vector.

—

#### Conclusion

$$
begin{align*}
boxed{r=sqrt{r^2_x+r^2_y}}
end{align*}
$$

Graphically:

Step 2

2 of 3

Result

3 of 3

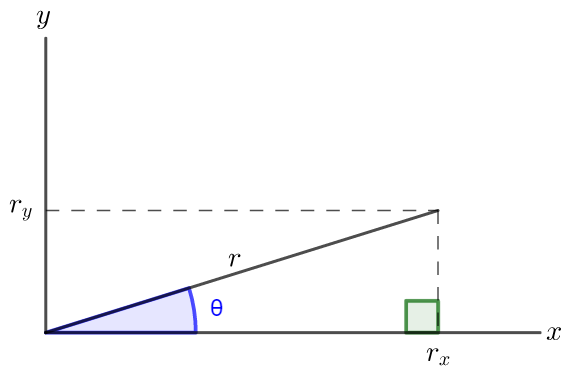
$$
begin{align*}
boxed{r=sqrt{r^2_x+r^2_y}}
end{align*}
$$

Exercise 13

Step 1

1 of 2

$newcommand{tx}$[1]${text{#1}}$

#### Known

A vector is defined by its length and direction.

Therefore:

When we solve a vector, it is because we know its length (magnitude) and direction.

—

#### Conclusion

To know its length and direction.

Result

2 of 2

To know its length and direction.

Exercise 14

Step 1

1 of 2

$newcommand{tx}$[1]${text{#1}}$

#### Known

For a vector $vec{r}$ with $r_x$ and $r_y$ components we have:

$$
begin{align*}
&r=sqrt{r^2_x+r^2_y} (tx{magnitude}) tx{and}\
&theta=tx{tan}^{-1}left(frac{r_y}{r_x}right) (tx{direction})
end{align*}
$$

#### Calculation

a) Therefore if the components are duplicated, the magnitude increases, this is:

$$
begin{align*}
r’=sqrt{(2 r_x)^2+(2 r_y)^2}=2 sqrt{r^2_x+r^2_y}=2 r
end{align*}
$$

$$
begin{align*}
boxed{r’=2 r}
end{align*}
$$

b) The direction angle is the same:

$$
begin{align*}
theta’=tx{tan}^{-1}left(frac{2 r_y}{2 r_x}right)=tx{tan}^{-1}left(frac{r_y}{r_x}right)=theta
end{align*}
$$

$$
begin{align*}
boxed{theta’=theta}
end{align*}
$$

#### Conclusion

a) The magnitude increases.

b) The direction angle is the same.

Result

2 of 2

a) The magnitude increases.

b) The direction angle is the same.

Exercise 15

Step 1

1 of 3

$newcommand{tx}$[1]${text{#1}}$

#### Known

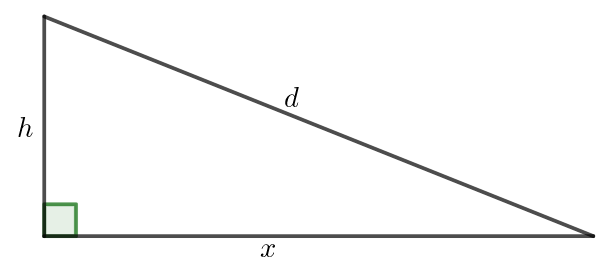
The Pythagorean theorem:

$$
begin{align}
d=sqrt{x^2+h^2}
end{align}
$$

#### Calculation

Givens: $h=24 tx{m}$, $x=320 tx{m}$

From (1):

$$
begin{align*}
d=sqrt{(320 tx{m})^2+(24 tx{m})^2}=321 tx{m}
end{align*}
$$

—

#### Conclusion

During the descent the plane covers a distance of $321 tx{m}$ meters.

Graphically:

Step 2

2 of 3

Result

3 of 3

During the descent the plane covers a distance of $321 text{m}$ meters.

Exercise 16

Step 1

1 of 3

$newcommand{tx}$[1]${text{#1}}$

#### Known

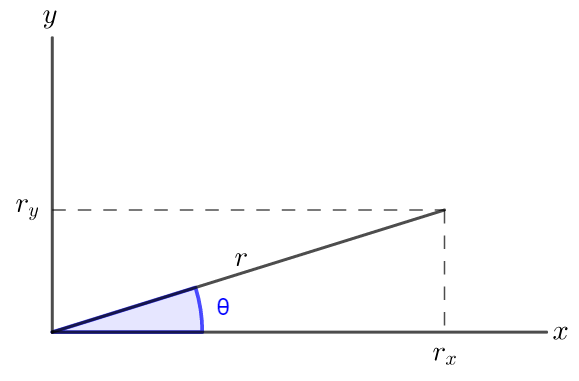
For the components of a vector, $r_x$ and $r_y$ and its magnitude r, the following relationships hold:

$$
begin{align*}
theta=tx{tan}^{-1}left(frac{r_y}{r_x}right) tx{or} theta=tx{sin}^{-1}left(frac{r_y}{r}right) tx{or} theta=tx{cos}^{-1}left(frac{r_x}{r}right)
end{align*}
$$

#### Calculation

Givens: $r=2.4 tx{km}=2.4times10^3 tx{m}$, $r_y=160 tx{m}$

Using:

$$
begin{align*}
theta=tx{sin}^{-1}left(frac{r_y}{r}right)=tx{sin}^{-1}left(frac{160 tx{m}}{2.4times10^3 tx{m}}right)=3.8^circ
end{align*}
$$

—

#### Conclusion

The angle of the road above the horizontal is $3.8^circ$.

Graphically:

Step 2

2 of 3

Result

3 of 3

The angle of the road above the horizontal is $3.8^circ$.

Exercise 17

Step 1

1 of 3

$newcommand{tx}$[1]${text{#1}}$

#### Known

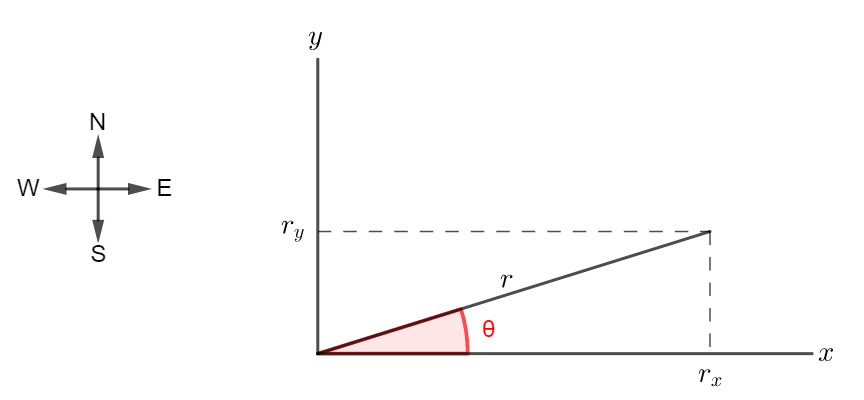
For a vector $vec{r}$, the components are given by:

$$
begin{align}
r_x=r tx{cos}(theta)hspace{0.5cm} tx{and}hspace{0.5cm} r_y=r tx{sin}(theta)
end{align}
$$

Where $theta$ is the angle that the vector makes with the positive x-axis.
#### Calculation

Givens: $r=760 tx{m}$, $theta=35^circ$ (north of east)

From (1):

$$
begin{align*}
&r_x=(760 tx{m}) tx{cos}(35^circ)=623 tx{m}\
&r_y=(760 tx{m}) tx{sin}(35^circ)=436 tx{m}
end{align*}
$$

—

#### Conclusion

$$
begin{align*}
boxed{r_x=623 tx{m}hspace{0.5cm} tx{and} hspace{0.5cm} r_y=436 tx{m}}
end{align*}
$$
.

Graphically:

Step 2

2 of 3

Result

3 of 3

$$
r_x=623 text{m}hspace{0.5cm} text{and} hspace{0.5cm} r_y=436 text{m}
$$

Exercise 18

Step 1

1 of 3

$newcommand{tx}$[1]${text{#1}}$

#### Known

The direction angle of a vector $vec{r}$ with components $r_x$ and $r_y$, is given by:

$$
begin{align}
theta=tx{tan}^{-1}left(frac{r_y}{r_x}right)
end{align}
$$

#### Calculation

Givens: $r_x=22 tx{m}$, $r_y=4.8 tx{m}$

From (1):

$$
begin{align*}
theta=tx{tan}^{-1}left(frac{4.8 tx{m}}{22 tx{m}}right)=12.3^circ
end{align*}
$$

—

#### Conclusion

$$
begin{align*}
boxed{theta=12.3^circ}
end{align*}
$$

Graphically:

Step 2

2 of 3

Result

3 of 3

The direction angle is $12.3^circ$.

unlock

All Solutions

Page 120: Lesson Check

Haven't found what you were looking for?

Search for samples, answers to your questions and flashcards