subsection*{Known}
For a vector $vec{d}$ with component $d_x$ and $d_y$, we have:
begin{align}
d&=sqrt{d^2_x+d^2_y}hspace{0.5cm} tx{and}hspace{0.5cm} tx{tan}(theta)=frac{d_y}{d_x}notag\
&implies theta=tx{tan}^{-1}left(frac{d_y}{d_x}right)
end{align}
subsection*{Calculation}
Givens: a) $d_x$, $d_y$, b) $d_x=2cdot 1.33 tx{m}=2.66 tx{m}$, $d_y=0.380 tx{m}$.\

From (1):\

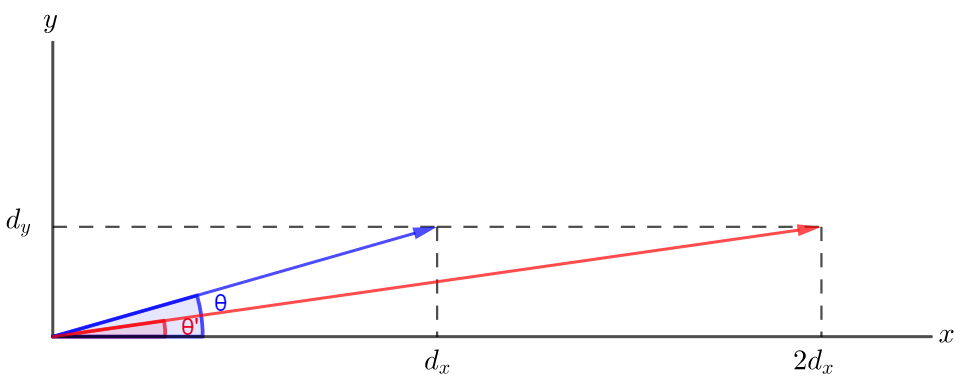
If $d_x$ (horizontal distance) is doubled:
begin{align*}
theta=tx{tan}^{-1}left(frac{d_y}{2d_x}right)impliestheta tx{decreases.}
end{align*}
Graphically:\

We see that $theta'<theta$.\

b)

$$
begin{align*}
theta=tx{tan}^{-1}left(frac{0.380 tx{m}}{2.66 tx{m}}right)=8.1^circ
end{align*}
$$

—

#### Conclusion

$$
begin{align*}
tx{a}) tx{The angle decreases} tx{b}) boxed{theta=8.1^circ}
end{align*}
$$

#### Known

The inclination of a vector $vec{r}$ with respect to the horizontal (x-axis).

$$
begin{align}
theta=tx{tan}^{-1}left(frac{r_y}{r_x}right)
end{align}
$$

#### Calculation

Given: For $r_y=1 tx{ft}$ and $r_x=100 tx{ft}$, we have $1%$ grade. Therefore, $6%$ grade $implies r_y=6 tx{ft} tx{and} r_x=100 tx{ft}$

From (1):

$$
begin{align*}
theta=tx{tan}^{-1}left(frac{6 tx{ft}}{100 tx{ft}}right)=3.4^circ
end{align*}
$$

—

#### Conclusion

$$
begin{align*}
boxed{theta=3.4^circ}
end{align*}
$$

subsection*{Known}

The magnitude of a vector $vec{r}$ is its length, that is, its size.
begin{align}
&tx{sin}(theta)=frac{tx{opposite side}}{tx{hypotenuse}}=frac{r_y}{r}notag\
&implies theta=tx{sin}^{-1}left(frac{r_y}{r}right)
end{align}
subsection*{Calculation}
Givens: $r=3.7 tx{m}$, $r_y=1.1 tx{m}$\

From (1):
begin{align*}
theta=tx{sin}^{-1}left(frac{1.1 tx{m}}{3.7 tx{m}}right)=17.3^circ
end{align*}
begin{align*}
boxed{theta=17.3^circ}
end{align*}

vspace{2pt}
hrule
vspace{1pt}

subsection*{Conclusion}

begin{align*}
boxed{theta=17.3^circ}
end{align*}

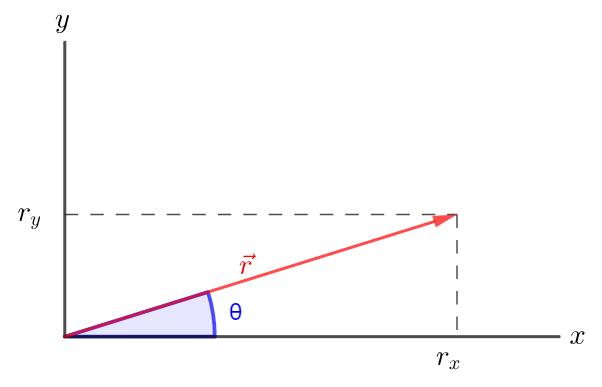
Graphically: