All Solutions
Page 117: Practice Problems
#### Known
The components of the displacement vector that forms an angle $theta$ with the positive x axis are given by:
$$
begin{align*}
d_x=d tx{cos}(theta)hspace{0.5cm} tx{and}hspace{0.5cm} d_y=d tx{sin}(theta)
end{align*}
$$
#### Calculation
Givens: $d=190 tx{m}$, $theta=15^circ$.
a)
$$
begin{align*}
d_x=d tx{cos}(theta)
end{align*}
$$
Therefore, for a smaller angle, the cosine of the angle increases, so the horizontal distance $d_x$ increases.
b)
$$
begin{align*}
d_x=(190 tx{m}) tx{cos}(15^circ)=183.5 tx{m}approx 184 tx{m}
end{align*}
$$
$$
begin{align*}
boxed{d_x=184 tx{m}}
end{align*}
$$
—
#### Conclusion
$$
begin{align*}
tx{a}) d_x tx{increases} tx{b}) boxed{d_x=184 tx{m}}
end{align*}
$$
begin{align*}
text{a}) d_x text{increases} text{b}) boxed{d_x=184 text{m}}
end{align*}
$$
#### Known
The components of a vector in a Cartesian $x-y$ coordinate system are the length of the vector on the $x$-axis and the length of the vector on the $y$-axis.
Therefore:
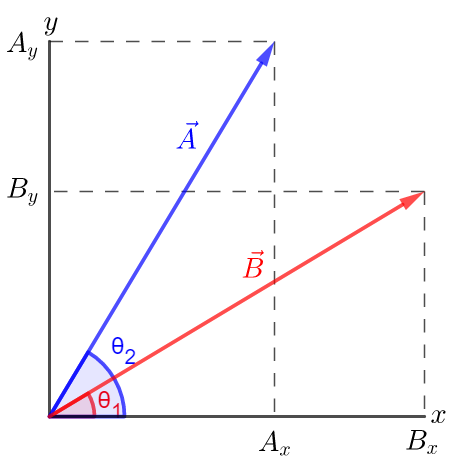
From the graph we can easily see that the $x$ component of vector $vec{B}$ is greater than $x$ component of vector $vec{A}$ and the $y$ component of vector $vec{A}$ is greater than the $y$ component of vector $vec{B}$.
Analytically this is:
$$
begin{align*}
&B_x>A_ximplies B tx{cos}(theta_1)>A tx{cos}(theta_2)\
&B_y<A_yimplies B tx{sin}(theta_1)<A tx{sin}(theta_2)
end{align*}
$$
With $theta_1<theta_2$ and $A=B$.
—
#### Conclusion
a) Vector $vec{B}$ has the larger $x$ component.
b) Vector $vec{A}$ has the larger $y$ component.
b) Vector $vec{A}$ has the larger $y$ component.
#### Known
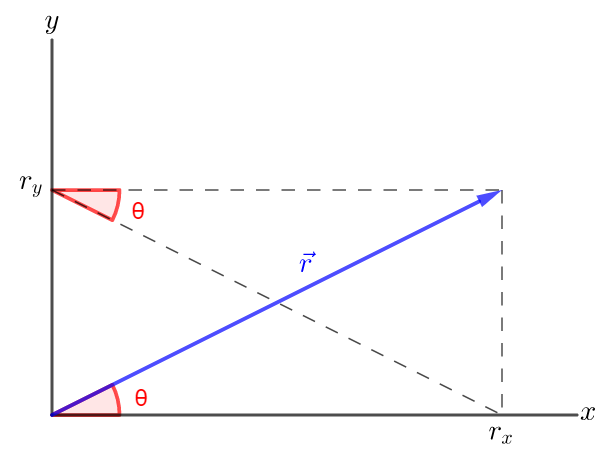
The components of a vector $vec{r}$ are given by:
$$
begin{align}
r_x=r tx{cos}(theta) tx{and} r_y=r tx{sin}(theta)
end{align}
$$
#### Calculation
Givens: $r=75.0 tx{m}$, a) $theta=35.0^circ$, b) $theta=65.0^circ$.
From (1)
a)
$$
begin{align*}
&r_x=(75.0 tx{m}) tx{cos}(35.0^circ)=61.4 tx{m}\
&r_y=(75.0 tx{m}) tx{sin}(35.0^circ)=43.0 tx{m}
end{align*}
$$
b)
$$
begin{align*}
&r_x=(75.0 tx{m}) tx{cos}(65.0^circ)=31.7 tx{m}\
&r_y=(75.0 tx{m}) tx{sin}(65.0^circ)=68.0 tx{m}
end{align*}
$$
—
#### Conclusion
$$
begin{align*}
&tx{a}) boxed{r_x=61.4 tx{m}} tx{and} boxed{r_y=43.0 tx{m}}\
&tx{b}) boxed{r_x=31.7 tx{m}} tx{and} boxed{r_y=68.0 tx{m}}
end{align*}
$$
begin{align*}
&text{a}) boxed{r_x=61.4 text{m}} text{and} boxed{r_y=43.0 text{m}}\
&text{b}) boxed{r_x=31.7 text{m}} text{and} boxed{r_y=68.0 text{m}}
end{align*}
$$
#### Known
The direction of a vector $vec{r}$ with respect to the x axis is given by:
$$
begin{align}
tx{tan}(theta)=frac{tx{opposite side}}{tx{adjacent side}}=frac{r_y}{r_x}
end{align}
$$
Where $theta$ is the angle that $vec{r}$ makes with x-axis.
The figure shows the problem situation.
#### Calculation
Givens: $r_y=9.75 tx{m}$ (press box), $theta=15.0^circ$, $r_x=?$ (second base)
From (1)
$$
begin{align*}
r_x=frac{r_y}{tx{tan}(theta)}=frac{9.75 tx{m}}{tx{tan}(15.0^circ)}=36.4 tx{m}
end{align*}
$$
$$
begin{align*}
boxed{r_x=36.4 tx{m}}
end{align*}
$$
—
#### Conclusion
Therefore, the horizontal distance from the press box to second base is $36.4 tx{m}$.
