
All Solutions
Page 111: Standardized Test Prep
#### Known
On a position-time graph, the slope of the line tangent to a curve at a point is equal to the velocity at that point (instantaneous velocity).
#### Calculation
Given: From the graph:
We can approximate the slope of the curve at $t=6 tx{s}$ (velocity at that time), as:
$$
begin{align*}
tx{slope}approx vapprox frac{x_f-x_i}{t_f-t_i}=frac{10 tx{m}-15 tx{m}}{6 tx{s}-5 tx{s}}=-5 frac{tx{m}}{tx{s}}
end{align*}
$$
$$
begin{align*}
boxed{vapprox-5 frac{tx{m}}{tx{s}}}
end{align*}
$$
—
#### Conclusion
Therefore, the answer is (D).
#### Known
On a position-time graph, the slope of the line tangent to a curve at a point is equal to the velocity at that point (instantaneous velocity).
#### Calculation
Givens: From the graph:
At $t=3 tx{s}$ there is a change in slope in the curve. From positive ($v>0$) for $t<3 tx{s}$ it becomes negative ($v3 tx{s}$.
—
#### Conclusion
Therefore, the answer is (A).
#### Known
$$
begin{align*}
x_f=x_i+v_icdot t+frac{acdot t^2}{2}, tx{for} a=tx{constant}
end{align*}
$$
#### Calculation
Givens: From the graph:
At $t=0 tx{s}$, $x=x_i=10 tx{m}$. Therefore options (C) and (D) are ruled out.
The object changes direction after three seconds. It goes from a positive velocity (positive slope) to a negative velocity (negative slope). From zero to three seconds, the object decelerates until its velocity is zero at $t=3 tx{s}$, that is, acceleration in the opposite direction to the positive velocity. From three to ten second, the velocity increases in the negative direction, that is, acceleration in the same direction as the negative velocity. Therefore, the acceleration of the object has to be negative.
This implies that the best equation is:
$$
begin{align*}
(tx{A}) boxed{x=10+6 t-t^2}
end{align*}
$$
Note that option (B) cannot be because the acceleration is positive and this would imply that the velocity would not change its initial positive direction.
—
#### Conclusion
$$
begin{align*}
(tx{A}) boxed{x=10+6 t-t^2}
end{align*}
$$
begin{align*}
(text{A}) boxed{x=10+6 t-t^2}
end{align*}
$$
#### Known
Acceleration in the same direction as the velocity, increase in velocity, acceleration in the opposite direction to velocity, decrease in velocity.
The acceleration of gravity can be considered constant and has a “downward” direction.
—
#### Conclusion
Therefore:
Option (C) may be correct, if the upward direction is regarded as negative and downward as positive. Option (D) may be correct, if the upward direction is considered as positive and downward as negative.
#### Known
Acceleration in the same direction as the velocity, increase in velocity, acceleration in the opposite direction to velocity, decrease in velocity.
The acceleration of gravity can be considered constant and has a “downward” direction.
—
#### Conclusion
Therefore, the correct answer is (C).
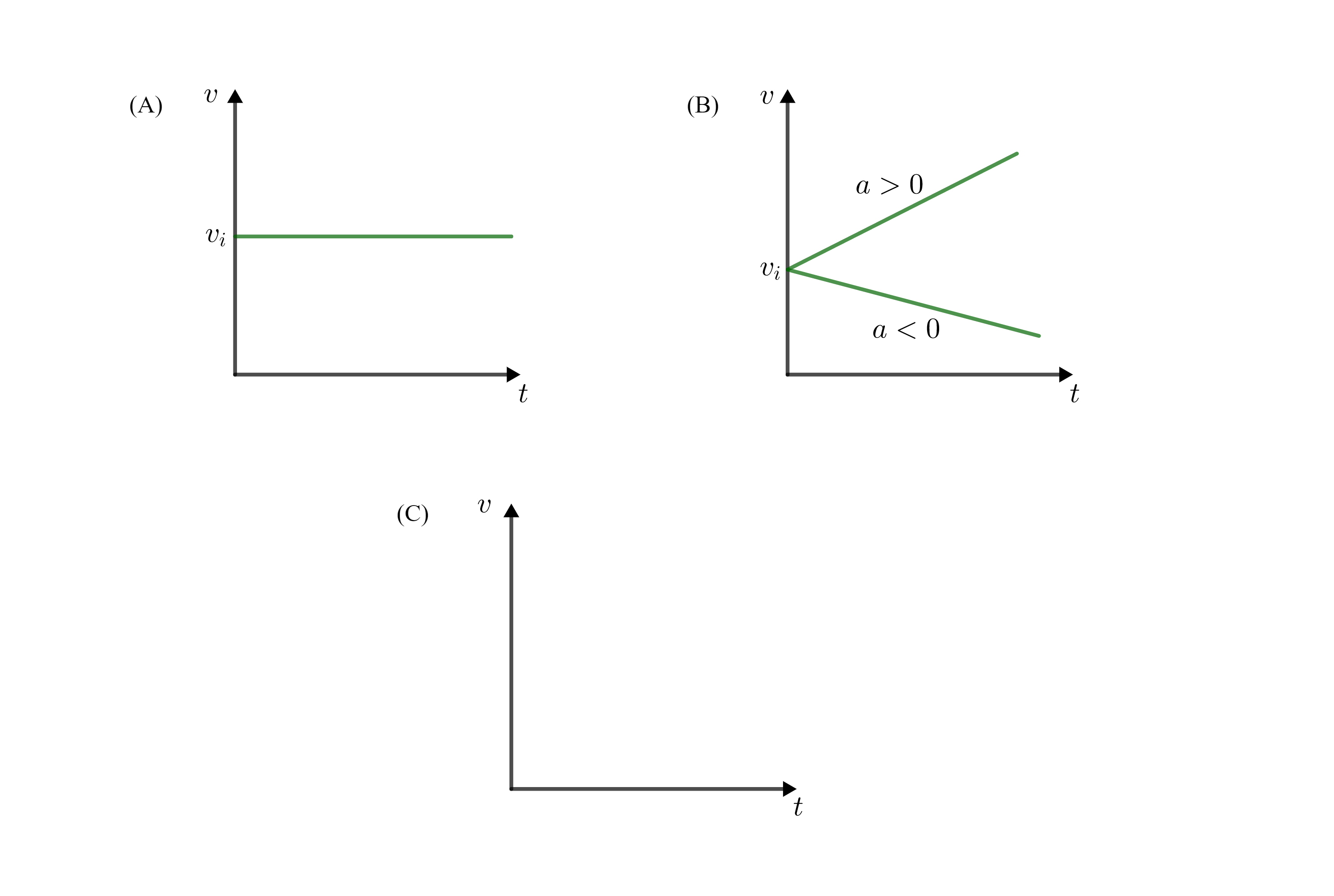
#### Known
On a velocity versus time graph, the slope of the curve at each point is equal to the acceleration at that point. When the acceleration is constant, the curve is a line of the form:
$$
begin{align*}
boxed{v_f=v_i+acdot t}
end{align*}
$$
Therefore:
When $a=0 frac{tx{m}}{tx{s}^2}$, we have:
$$
begin{align*}
boxed{v_f=v_i=tx{const}}
end{align*}
$$
This is a line of zero slope.
When $a=tx{const}neq 0$, we have:
$$
begin{align*}
boxed{v_f=v_i+acdot t}
end{align*}
$$
This is a line with slope $a$.
When $v_i=0 frac{tx{m}}{tx{s}}$ and $a=0 frac{tx{m}}{tx{s}^2}$, we have:
$$
begin{align*}
boxed{v_f=0 frac{tx{m}}{tx{s}}}
end{align*}
$$
Everything seen above is valid, so the correct answer is (D).
—
#### Conclusion
The correct answer is (D).
The graphics of each option are shown below.
#### Known
Acceleration in the same direction as the velocity, increase in velocity, acceleration in the opposite direction to velocity, decrease in velocity.
#### Calculation
Using:
$$
begin{align*}
v_f=v_i+acdot t
end{align*}
$$
When $a=0 frac{tx{m}}{tx{s}^2}$ (in this case zero would be the constant value of the acceleration), we have:
$$
begin{align*}
boxed{v_f=v_i=tx{const}}
end{align*}
$$
When the direction of the acceleration and the initial velocity is the same, we have:
$$
begin{align*}
v_f=v_i+acdot thspace{0.5cm} tx{or}hspace{0.5cm} v_f=-v_i-acdot t
end{align*}
$$
That is, the object increases its velocity in the positive or negative direction (what we define as the positive or negative direction).
When the direction of the acceleration and the initial velocity is opposite, we have:
$$
begin{align*}
v_f=v_i-acdot thspace{0.5cm} tx{or}hspace{0.5cm} v_f=-v_i+acdot t
end{align*}
$$
That is, the object decreases its velocity in the positive or negative direction (what we define as the positive or negative direction).
Therefore option (D) is correct. Since all of the above are possible.
—
#### Conclusion
The correct answer is (D).
#### Known
The acceleration of gravity is approximately constant near the surface of the Earth and is directed toward the center of the Earth. Thus:
The acceleration:
When the student throws the ball upwards with an initial velocity $v_i$, it will move with the acceleration of gravity downwards $left( aapprox -9.81 frac{tx{m}}{tx{s}^2}right)$, during the entire trajectory of the ball, whether is ascending or descending.
The velocity:
When the ball is thrown upward (assuming a positive direction), its velocity begins to decrease since the acceleration is downward. As the ball passes through a tree limb, the velocity continues upwards and can be determined by either $boxed{v_f=v_i+gcdot t tx{or} v_f=sqrt{v^2_i+2gcdot h}, left( g= -9.81 frac{tx{m}}{tx{s}^2}right)}$. Where $h$ is the height of the branch with respect to us and $t$ is the time it takes the ball to reach that position. Once the ball passes the branch, it will continue to climb until it stops $(v_f = 0)$. We can calculate this height by either $boxed{h=-frac{v^2_i}{2g} tx{or} h=v_icdot t+frac{gcdot t^2}{2}, left( g= -9.81 frac{tx{m}}{tx{s}^2}right)}$. When the ball begins to descend, its velocity begins to increase in the negative direction (downward), since it has the same direction as the downward acceleration. All the downward movement of the ball will be the same as upward (symmetry), that is, the ball will take the same time to return to the student’s hand from the maximum height, as it did to go from the student’s hand up to maximum height. As for the speed of the ball while it falls, it will have the same value when passing through the branch as when it went up, only now in the opposite direction, so that when returning to the student’s hand, the final speed of the ball will be equal to minus the initial velocity of the ball, $(v_i=-v_f)$.
From the previous explanation, we see that the speed (a scalar) at each point of the upward trajectory is the same as the downward trajectory, this due to the symmetry of the problem (objects in free fall).
Note that the entire description above is without considering air resistance.
—
#### Conclusion
The acceleration is constant, with a downward direction. The velocity decreases as the ball ascends until it becomes zero at maximum height. In the descent, the velocity takes the same values at each point as when the ball was ascending, the only difference is in its directions. With speed it happens the same as in velocity, only without the change of direction since it is a scalar.

