Home Page Textbooks Physics: Principles and Problems Page 95: Section Review

Physics: Principles and Problems

9th Edition

Elliott, Haase, Harper, Herzog, Margaret Zorn, Nelson, Schuler, Zitzewitz

ISBN: 9780078458132

Textbook solutions

All Solutions

Page 95: Section Review

Exercise 9

Result

1 of 1

mass (c), inertia (c), push of a hand (a), friction (a), air resistance (a), spring force (a), gravity (b),
acceleration (c)

Exercise 10

Solution 1

Solution 2

Step 1

1 of 2

$textbf{Inertia can be felt.}$ You can feel the inertia of a pencil or a book through your hand. Without an outside force acting upon either objects, they will remain at rest unless you apply a force that will change these objects’ velocity.

Result

2 of 2

$$
textbf{Inertia can be felt in both a pencil and a book.}
$$

Step 1

1 of 2

The answer is $textbf{yes, in both cases}$. We can feel the inertia of any object. In order to move an object we have to change its speed, which means we have to accelerate it. $textbf{When we accelerate an object, we act on it by some force}$, and according to $textbf{Newton’s third law}$, then the object also acts on us by a force of equal amount and in the opposite direction. The difference between a book and a pen is that they have different masses, so the forces they act on us will be different.

Result

2 of 2

The answer is yes in both cases.

Exercise 11

Step 1

1 of 2

System:Bag of sugar

Agents:Hand, Earth

$F_g$ force of gravity

$F_h$ force of hand acting upon bag

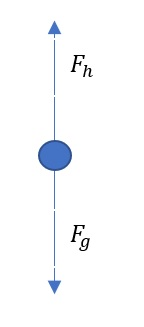
Exercise scan

Result

2 of 2

See the explanation.

Exercise 12

Step 1

1 of 2

If we act with some force on the book in forward direction, it does $textbf{not necessarily}$ mean that it will accelerate in that direction. It is possible that the $textbf{book moves backwards}$, if we then $textbf{act on the book forwards}$, we will $textbf{slow down the book}$ but it will still move in the $textbf{opposite direction of the force}$.

Result

2 of 2

Not necessarily.

Exercise 13

Step 1

1 of 2

System: Bucket with water

Agents: Earth, rope

$F_g$ force of gravity

$F_r$ force which rope acts on bucket

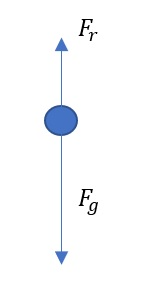
Exercise scan

Result

2 of 2

See the explanation.

Exercise 14

Step 1

1 of 4

The key detail we read from the problem is that a force of $1 mathrm{N}$ is the only force acting on the block. This tells us that it is this force that is the cause of the acceleration.

The second newtonow law gives us an expression for acceleration:

$$
F=ma rightarrow a=dfrac{F}{m}
$$

Step 2

2 of 4

Known:

$$
begin{align*}
a_2&=3a_1\
F&=1 mathrm{N}
end{align*}
$$

Unknown:
$$
m_1=xm_2
$$

Step 3

3 of 4

Now let us just include the known in the expression for acceleration:

$$
begin{align*}
a_2&=3a_1 \
dfrac{1 mathrm{N} }{m_2}&=3dfrac{1 mathrm{N} }{m_1}
end{align*}
$$

Multiply the above expression by $m_1 m_2$ and the force cancel out:

$$
begin{align*}
dfrac{m_1m_2}{m_2}&=3dfrac{m_1m_2 }{m_1}\
m_1 &= 3 m_2\
x&=3
end{align*}
$$

Result

4 of 4

The mass of the first block is three times larger

unlock

All Solutions

Page 95: Section Review

Haven't found what you were looking for?

Search for samples, answers to your questions and flashcards