Home Page Textbooks Physics: Principles and Problems Page 396: Assessment

Physics: Principles and Problems

9th Edition

Elliott, Haase, Harper, Herzog, Margaret Zorn, Nelson, Schuler, Zitzewitz

ISBN: 9780078458132

Textbook solutions

All Solutions

Page 396: Assessment

Exercise 31

Step 1

1 of 1

Exercise 32

Step 1

1 of 2

Periodic motion is motion which is repeating in the same way during the time.

Examples are: oscillating spring, pendulum, uniform rotation etc.

Result

2 of 2

Periodic motion is motion which is repeating in the same way during the time and its examples are oscillating spring, pendulum, uniform rotation…

Exercise 33

Step 1

1 of 2

Frequency is a physical quantity which describes number of vibrations during the time, its unit is $textit{Herz}$ $mathrm{Hz}$.

Period is physical quantity that shows time which is taken for one cycle of oscillation. Unit is $textit{second}$ $mathrm{s}$.

Result

2 of 2

Frequency shows number of vibrations or cycles during the time.

Period is time which is taken for one cycle of oscillation.

Exercise 34

Step 1

1 of 2

Simple harmonic motion is motion that is repeating during the time, back and forth, through the state of balance, in such a way that maximum displacement on the one side equals the maximum displacement on the other side.

Examples of simple harmonic motion is: pendulum.

Result

2 of 2

Simple harmonic motion is motion that is repeating during the time, back and forth, through the state of balance, in such a way that the maximum displacement on the one side equal maximum displacement on the other one. Example is: pendulum.

Exercise 35

Step 1

1 of 2

Hooke’s law states that: stretched distance is proportional to the force which is stretching or compressing the spring:

$$
F = (-)kx
$$

In the previous equation:

$F$ – force

$k$ – spring constant

$x$ – stretched (compressed) distance

Therefore, we can conclude that the spring obeys Hooke’s law if its stretched (compressed) distance is proportional to the force which has caused the stretch (compression).

Result

2 of 2

Spring will obey Hooke’s law if the stretched or compressed distance is proportional to the force which has caused it.

Exercise 36

Step 1

1 of 2

Spring constant of the spring is the slope on the force versus displacement graph.

Result

2 of 2

It is the slope on the force versus displacement graph.

Exercise 37

Step 1

1 of 2

Since there is a curved line on the force versus displacement graph, potential energy will be area under that curve.

Result

2 of 2

Potential energy is area under the curved line.

Exercise 38

Step 1

1 of 2

Period of a pendulum does not depend on the mass of the bob, but it does depend on the length of the spring and gravitation acceleration since it is given by:

$$
T = sqrt{dfrac{l}{g}}
$$

Where:

$l$ – length of the spring

$g$ – gravitational acceleration

Result

2 of 2

It does not depend on the mass of the bob, but does depend on the length of the spring and gravitational acceleration.

Exercise 39

Step 1

1 of 2

Resonance will occur when force which acts on the system that oscillates has frequency which is the same as the natural frequency of that system.

Result

2 of 2

Force which acts on the system that oscillates has to have the same frequency as the natural frequency of that system is.

Exercise 40

Step 1

1 of 2

There are two general methods of energy transfer:

1. by waves (rays of light and sound)

2. by particle transfer (bullet)

Result

2 of 2

Two methods: by waves and by particle transfer.

Exercise 41

Step 1

1 of 2

Primary difference between a mechanical and electromagnetic wave is that mechanical waves cannot travel through the vacuum, they need a medium and electromagnetic waves can travel through the vacuum.

Result

2 of 2

Mechanical waves cannot travel through the vacuum, they need a medium and electromagnetic waves can travel through the vacuum.

Exercise 42

Step 1

1 of 2

Transverse waves are waves which oscillations are perpendicular to the direction at which wave travels.(particles are moving up and down)

Longitudinal waves are waves which oscillations are parallel to the direction at which wave travels.(particles are moving back and forth)

Surface waves are combination of both of them.

Result

2 of 2

Oscillations of transverse waves are perpendicular to the direction at which wave travels and oscillations of longitudinal waves are parallel to the direction at which wave travels. Surface waves are combination of both of them.

Exercise 43

Step 1

1 of 2

$textit{a.}$, Speed cannot be change since it only depends on medium which cannot be changed.

$textit{b.}$, Frequency can be changed since the frequency at which waves are produced can be changed.

Result

2 of 2

$textit{a.}$, It can’t be changed since it depends on medium which cannot be change.

$textit{b.}$, It can be change since the frequency at which waves are produced can be changed.

Exercise 44

Step 1

1 of 1

Wavelength is the distance between two identical points on a wave which are in the same phase.

Exercise 45

Step 1

1 of 1

Initial and final position of the point will be the same after the pulse has passed.

Exercise 46

Step 1

1 of 1

In the case of wave pulse, wave disturbs particles perpendicular to the direction in which the wave travels and in the case of periodic wave, disturbance is parallel to the direction in which wave travels.

Exercise 47

Step 1

1 of 1

They differ because frequency is number of vibrations per second and velocity is speed at which wave travels through the medium.

Exercise 48

Step 1

1 of 2

Frequency of our hand will be equal to the frequency of the wave.

Result

2 of 2

These two will be equal.

Exercise 49

Step 1

1 of 1

Two points are in phase when they have $text{color{#c34632}same displacement}$ and $text{color{#c34632}same speed}$

They are out of phase if they are not in phase.

Example : Two crests are in phase with each other

And a crest and a trough are out of phase

Exercise 50

Solution 1

Solution 2

Step 1

1 of 2

Amplitude is maximum displacement of a wave from its equilibrium position

Step 2

2 of 2

Amplitude represents the amount of energy transferred by the wave

Step 1

1 of 1

Amplitude of a wave is its maximum displacement from the equilibrium position.

Exercise 51

Step 1

1 of 2

Amplitude of a wave and the energy it carries are proportional.

Result

2 of 2

These two are proportional.

Exercise 52

Step 1

1 of 1

When wave reaches a boundary of a new medium, part of the wave is reflected back, part of the wave is transmitted into the new medium and part of its energy is being absorbed.

Exercise 53

Step 1

1 of 2

When a wave crosses a boundary between a thin and thick rope since the wave is both being transmitted and reflected, frequency remains the same.

Result

2 of 2

Frequency stays the same since wave is being both reflected and transmitted.

Exercise 54

Step 1

1 of 1

Main difference between these two is that the reflected pulse is inverted.

Exercise 55

Step 1

1 of 2

Interference is phenomenon in physics which is superposition of two or more waves and it is property of all types of waves.

Interference can be either constructive or destructive; it is constructive in the case of superposition of waves which have same amplitudes in the same direction, those waves are in phase, and it is destructive when those waves have opposite amplitudes, are in opposite phases.

Result

2 of 2

Interference is superposition of two or more waves and is property of all types of waves.

Exercise 56

Step 1

1 of 2

Nothing will happen to a spring at the nodes of a standing wave.

Result

2 of 2

Nothing will happen.

Exercise 57

Step 1

1 of 2

Areas where there is no sugar are regions of antinode where the vibration reaches its maximum and regions covered in sugar are nodal regions and in that place vibrations are not produced.

Result

2 of 2

Regions without sugar are regions of antinode and there are maximum vibrations and the ones covered in sugar are nodal regions where there are no vibrations.

Exercise 58

Solution 1

Solution 2

Step 1

1 of 1

This happens because the standing wave is being formed and string can be touched at any of its five nodal points.

Step 1

1 of 1

Standing wave exists and the string can be touched at any of its five nodal points

Exercise 59

Step 1

1 of 1

Two changes are changes in wavelength and direction and what does not change is frequency.

Exercise 60

Step 1

1 of 2

Energy changes that take place during one complete cycle:

At the beginning of this very motion, elastic potential energy has maximum value, gravitational potential energy has minimum value and kinetic energy equals zero.

When the ball reaches equilibrium position elastic potential energy will be zero, but kinetic energy will reach its maximum value.

Gravitational potential energy will reach its maximum value as the ball reaches highest point of the motion along with the potential energy and kinetic energy will be zero, therefore, we can conclude that total mechanical energy is conserved and did not change.

Result

2 of 2

Total mechanical energy will not change.

Exercise 61

Step 1

1 of 2

Since the International space station is in free fall where value of gravitational acceleration is zero, pendulum clock cannot be used there.

Result

2 of 2

It cannot be used.

Exercise 62

Step 1

1 of 2

When direction is parallel to its length, waves are longitudinal and when direction is at right angles to its length, waves are transverse.

Result

2 of 2

In the first case waves are longitudinal and in the second one they are transverse.

Exercise 63

Step 1

1 of 2

As we move our finger faster wavelength will decrease.

Result

2 of 2

Wavelength will decrease.

Exercise 64

Step 1

1 of 2

Since frequency and period are inversely proportional, when the frequency increases, period will decrease.

Result

2 of 2

Period will decrease.

Exercise 65

Step 1

1 of 2

Since wavelength and frequency are inversely proportional, when the frequency increases, wavelength will decrease.

Result

2 of 2

Wavelength will decrease.

Exercise 66

Step 1

1 of 2

Since energy is directly proportional to the amplitude squared, with twice amplitude, four times energy will be required to create a pulse.

Result

2 of 2

Four times energy is required.

Exercise 67

Step 1

1 of 2

Since the period of vibration is the time in which wave moves across the pan and constructive interference will be produced.

Result

2 of 2

Period of vibration is the time in which wave moves across the pan and constructive interference will be produced.

Exercise 68

Step 1

1 of 2

Boundaries $A$ and $B$ are more rigid and $C$ and $D$ are less rigid.

Result

2 of 2

$A$ and $B$ – more rigid

$C$ and $D$ – less rigid

Exercise 69

Step 1

1 of 2

Information given in the text are:

$x = 0.12, mathrm{m}$

$F = 3.2, mathrm{N}$

Force is given by the following equation:

$$
F = kx
$$

We can express $k$ from the previous equation:

$$
k = dfrac{F}{x}
$$

When we put known values into the previous equation we get:

$$
k = dfrac{3.2, mathrm{N}}{0.12, mathrm{m}}
$$

$$
boxed{k = 27, mathrm{N/m}}
$$

Result

2 of 2

$$
k = 27, mathrm{N/m}
$$

Exercise 70

Step 1

1 of 2

Information given in the text are:
– $k = 25000, mathrm{N/m}$
– $F = 12000, mathrm{N}$

Force is given by:
$$F = kx$$
We can express $x$ from the previous equation:
$$x = dfrac{F}{k}$$
When we put known values into the previous equation we get:
$$x = dfrac{12000, mathrm{N}}{25000, mathrm{N/m}}$$
$$boxed{x = 0.48, mathrm{m}}$$

Result

2 of 2

$$x = 0.48, mathrm{m}$$

Exercise 71

Step 1

1 of 2

We should use $PE_{sp}=dfrac{1}{2} k x^{2}$ equation ;

So;

$PE_{sp}=dfrac{1}{2} k x^{2} =( dfrac{1}{2} ) (27N/m) (0.16m)^{2} = 0.35J$

Result

2 of 2

$textit$$text{color{#c34632} 0.35J $ $}$

Exercise 72

Step 1

1 of 2

We should use $PE_{sp}=dfrac{1}{2} k x^{2}$ equation ;

So,from above equation ;

$x=sqrt{dfrac{2PE_{sp}}{k}} = sqrt{dfrac{(2)(1.5J)}{35 N/m}} = 0.29m$

Result

2 of 2

$textit$$text{color{#c34632} 0.29m $$}$

Exercise 73

Solution 1

Solution 2

Step 1

1 of 2

The spring constant is equal to the slope of the F-x diagram:

$k = slope = dfrac{12.0}{0.60} = 20 N/m$

$$
E = (1/2) k x^2 = (1/2) * (20) * (0.50)^2 = 2.5 J
$$

Result

2 of 2

a) $20 N/m$

b) $2.5 J$

Step 1

1 of 8

**Given:**
– The force: $F_1 = 4 mathrm{~N}$;
– The distance: $x_1 = 0.2 mathrm{~m}$;
– The force: $F_2 = 8 mathrm{~N}$;
– The distance: $x_2 = 0.4 mathrm{~m}$;

**Required:**

a) The constant of the spring $k$;

b) The potential energy of the spring $PE_text{sp}$;

Step 2

2 of 8

Force-versus-length graph is a linear graph. A linear graph is represented as a straight line and described mathematically as:
$$y = kx + l$$

Step 3

3 of 8

**a)** In the equation above $y$ represents where we are on the $y$-axis if we are at $x$ on $x$-axis. $k$ is the constant of proportionality, or in our case the slope of the graph. $l$ is the $y$-intercept. Our graph looks like this:

![‘slader’](https://slader-solution-uploads.s3.amazonaws.com/e20f9121-474d-4841-a962-64466d004abe-1650140272624763.png)

Step 4

4 of 8

The two dots are the two points for the change we will observe. On the $y$-axis we have force, constant of proportionality, $k$, is the spring constant, $x$-axis is the length and the $y$-intercept is zero. We actually got the equation for spring force:
$$F = kx$$

Step 5

5 of 8

The slope is defined as a ratio of how much the $y$ coordinate changes for a change in the $x$ coordinate. Solving the equation above for $k$, we divide it by $x$
$$k = frac{Delta F}{Delta x}$$

Step 6

6 of 8

Plugging in the numbers:
$$begin{align*}
k &= frac{F_2 – F_1}{x_2 – x_1} \
&= frac{8 mathrm{~N} – 4 mathrm{~N}}{0.4 mathrm{~m} – 0.2 mathrm{~m}} \
&= 20 ,frac{text{N}}{text{m}}
end{align*}$$
$$boxed{k = 20 ,frac{text{N}}{text{m}}}$$

Step 7

7 of 8

**b)** The energy stored in the spring equals the work done on the spring. The work done is the product of the force exerted over some distance. It is also the area under the $F – x$ graph, in this case, a triangle whose area can be calculated as one-half of the base times height. When the spring is stretched to $50 mathrm{~cm}$, the force is $10 mathrm{~N}$. Now we have all the data needed:
$$begin{align*}
PE_text{sp} &= frac{Fx}{2} \
&= frac{50 mathrm{~cm} cdot 10 mathrm{~N}}{2} \
&= frac{0.5 mathrm{~m} cdot 10 mathrm{~N}}{2} \
&= 2.5 mathrm{~J}
end{align*}$$
$$boxed{ PE_text{sp} = 2.5 mathrm{~J}}$$

Result

8 of 8

$$begin{align*}
&text{a) } k = 20 ,frac{text{N}}{text{m}} \
&text{b) } PE_text{sp} = 2.5 mathrm{~J}
end{align*}$$

Exercise 74

Step 1

1 of 2

Information given in the text are:

$T = 2.3, mathrm{s}$

$g = 1.6, mathrm{m/s^{2}}$

$l = ?$

Period is given by:

$$
T = 2 pi sqrt{dfrac{l}{g}}
$$

We can easily express $l$ from the previous equation:

$$
l = dfrac{T^{2}g}{4 pi^{2}}
$$

When we put known values into the previous equation we get:

$$
l = dfrac{(2.3, mathrm{s})^{2} cdot (1.6, mathrm{m/s^{2}})}{4 pi^{2}}
$$

Finally:

$$
boxed{l = 0.21, mathrm{m}}
$$

Result

2 of 2

$$
l= 0.21, mathrm{m}
$$

Exercise 75

Step 1

1 of 2

Information given in the text are:

$f = 0.12, mathrm{Hz}$

Period is given by:

$$
T = dfrac{1}{f}
$$

When we put known value into the previous equation and when we express $mathrm{Hz}$ as $dfrac{1}{s}$ we get:

$$
T = dfrac{1}{0.12, mathrm{dfrac{1}{s}}}
$$

$$
boxed{T = 8.3, mathrm{s}}
$$

Result

2 of 2

$$
T = 8.3, mathrm{s}
$$

Exercise 76

Step 1

1 of 2

Information given in the text are:

$lambda= 12, mathrm{m}$

$T = 3, mathrm{s}$

$v= ?$

Since wavelength is given by:

$$
lambda = dfrac{v}{f}
$$

And frequency is given by:

$$
f = dfrac{1}{T}
$$

Speed, expressed by these equations will be:

$$
v = lambda f = lambda dfrac{1}{T}
$$

When we put known values into the previous equation we get:

$$
v = 12, mathrm{m} cdot dfrac{1}{3, mathrm{s}}
$$

$$
boxed{v= 4, mathrm{m/s}}
$$

Result

2 of 2

$$
v= 4, mathrm{m/s}
$$

Exercise 77

Step 1

1 of 3

Information given in the text are:

$lambda = 0.06, mathrm{m}$

$f = 4.8, mathrm{1/s} = 4.8, mathrm{Hz}$

$textit{a.}$, $v=?$

Since wavelength is given by:

$$
lambda = dfrac{v}{f}
$$

Speed, expressed by the previous equation will be:

$$
v = lambda f
$$

When we put known values into the previous equation we get:

$$
v = 0.06, mathrm{m} cdot 4.8, mathrm{Hz}
$$

$$
boxed{v= 0.29, mathrm{m/s}}
$$

Step 2

2 of 3

$textit{b.}$, $T = ?$

Period is given by:

$$
T = dfrac{1}{f}
$$

When we put known values into the previous equation we get:

$$
T = dfrac{1}{4.8, mathrm{Hz}}
$$

$$
boxed{T = 0.21, mathrm{s}}
$$

Result

3 of 3

$textit{a.}$, $v= 0.29, mathrm{m/s}$

$textit{b.}$, $T = 0.21, mathrm{s}$

Exercise 78

Solution 1

Solution 2

Step 1

1 of 2

$v = dfrac{d}{t} = dfrac{3.4}{1.8} = 1.9 m/s$

$$
lambda = v T = (1.9) * (1.1) = 2.1 m
$$

Result

2 of 2

a) $1.9 m/s$

b) $2.1 m$

Step 1

1 of 5

**Given:**
– Distance: $s = 3.4 mathrm{~m}$
– Time: $t = 1.8 mathrm{~s}$;
– Period: $T = 1.1 mathrm{~s}$;

**Required:**

a) Wave speed $v$;

b) Wavelength of the water wave $lambda$;

Step 2

2 of 5

Water waves spread out at a constant speed given as the ratio of distance traveled and the time needed to travel that distance. We have an equation that relates the wave speed, wavelength, and frequency. The period can be found as the reciprocal of the frequency:
$$begin{align*}
v &= frac{s}{t}&&(1) \
v &= lambda f &&(2) \
T &= frac{1}{f} &&(3)
end{align*}$$

Step 3

3 of 5

**a)** The speed of the water waves can be found using the first equation. Plugging in the numbers we have:
$$begin{align*}
v &= frac{s}{t} \
&= frac{3.4 mathrm{~m}}{1.8 mathrm{~s}} \
&= 1.9 ,frac{text{m}}{text{s}}
end{align*}$$
$$boxed{ v = 1.9 ,frac{text{m}}{text{s}} }$$

Step 4

4 of 5

**b)** Solving for $lambda$ we divide the second equation by $f$ and combine it with the third equation:
$$begin{align*}
lambda &= frac{v}{f} \
&= vT \
&= 1.9 ,frac{text{m}}{text{s}} cdot 1.1 mathrm{~s} \
&= 2.1 mathrm{~m}
end{align*}$$
$$boxed{ lambda = 2.1 mathrm{~m} }$$

Result

5 of 5

$$begin{align*}
&text{a) } v = 1.9 ,frac{text{m}}{text{s}}\
&text{b) } lambda = 2.1 mathrm{~m}
end{align*}$$

Exercise 79

Step 1

1 of 4

Information given in the text are:

$1 cdot 10^{6}, mathrm{Hz}$

$lambda = 1.5, mathrm{mm} = 1.5 cdot 10^{-3}, mathrm{m}$

$textit{a.}$, $v = ?$

Since wavelength is given by:

$$
lambda = dfrac{v}{f}
$$

We can easily express $v$ from the previous equation:

$$
v = lambda f
$$

When we put known values into the previous equation we get:

$$
v = 1.5 cdot 10^{-3}, mathrm{m} cdot 1 cdot 10^{6}, mathrm{Hz}
$$

$$
boxed{v = 1.5 cdot 10^{3}, mathrm{m/s}}
$$

Step 2

2 of 4

$textit{b.}$, $T=?$

Period is given by:

$$
T = dfrac{1}{f}
$$

When we put known values into the previous equation we get:

$$
T = dfrac{1}{1 cdot 10^{6}, mathrm{Hz}}
$$

$$
boxed{T = 1 cdot 10^{-6}, mathrm{s}}
$$

Step 3

3 of 4

$textit{c.}$, $T_{air}=?$

Period along with the frequency remains the same.

Result

4 of 4

$textit{a.}$, $v = 1.5 cdot 10^{3}, mathrm{m/s}$

$textit{b.}$, $T = 1 cdot 10^{-6}, mathrm{s}$

$textit{c.}$, Period along with the frequency remains the same.

Exercise 80

Solution 1

Solution 2

Step 1

1 of 2

$f = dfrac{v}{lambda} = dfrac{330}{0.60} = 550 Hz$

The frequency is 550 Hz therefore 550 waves are emitted per second and 275 waves every 0.50 s.

$$
d = v t = (330)*(0.50) = 165 m
$$

Result

2 of 2

a) $550 Hz$

b) 275 waves

c) $165 m$

Step 1

1 of 6

**Given:**
– Wavelength: $lambda = 0.6 mathrm{~m}$;
– Velocity: $v = 330 ,frac{text{m}}{text{s}}$;
– Time: $t = 0.5 mathrm{~s}$;

**Required:**

a) Frequency $f$;

b) Number of complete waves $n$;

c) Distance from the source $s$;

Step 2

2 of 6

We have an equation that relates the wave speed, wavelength, and frequency. The number of complete waves is a product of the frequency of the wave and the time passed. Water waves spread out at a constant speed, given as the ratio of distance traveled and the time needed to travel that distance.
$$begin{align*}
v &= lambda f &&(1) \
n &= ft &&(2) \
v &= frac{s}{t}&&(3) \
end{align*}$$

Step 3

3 of 6

**a)** To find the frequency of the wave, we solve the first equation for $f$ by dividing it by $flambda$:
$$begin{align*}
f &= frac{v}{lambda } \
&= dfrac{330 ,frac{text{m}}{text{s}}}{0.6 mathrm{~m}} \
&= 550 mathrm{~Hz}
end{align*}$$
$$boxed{ f = 550 mathrm{~Hz} }$$

Step 4

4 of 6

**b)** If we are interested in the number of complete waves we need to multiply the frequency of the wave with the time interval we are observing:
$$begin{align*}
n &= ft \
&= 550 mathrm{~Hz} cdot 0.5 mathrm{~s} \
&= 275
end{align*}$$
$$boxed{ n = 275 }$$

Step 5

5 of 6

**c)** The distance the wave travels can be determined from the third equation for constant velocity equation. Solving it for $s$ we multiply it by $t$:
$$begin{align*}
s &= vt \
&= 330 ,frac{text{m}}{text{s}} cdot 0.5 mathrm{~s} \
&= 165 mathrm{~m}
end{align*}$$
$$boxed{ s = 165 mathrm{~m} }$$

Result

6 of 6

$$begin{align*}
&text{a) } f = 550 mathrm{~Hz}\
&text{b) } n = 275 \
&text{c) } s = 165 mathrm{~m}
end{align*}$$

Exercise 81

Step 1

1 of 2

The signal arrives to the bottom of the water after 0.90 s:

$$
d = v t = (1498) * (0.9) = 1350 m
$$

Result

2 of 2

$$
1350 m
$$

Exercise 82

Solution 1

Solution 2

Step 1

1 of 2

$f = frequency = dfrac{12}{20.0} = 0.6 Hz$

$lambda = wavelength = (2)*(3.0) = 6.0 m$

$$
v = speed = lambda f = (6.0)*(0.6) = 3.6 m/s
$$

Result

2 of 2

$$
3.6 m/s
$$

Step 1

1 of 6

**Given:**
– Distance: $d = 3 mathrm{~m}$;
– Number of waves: $n = 12$;
– Time: $t = 20 mathrm{~s}$;

**Required:**
– The speed of waves $v$;

Step 2

2 of 6

We have an equation that relates the wave speed, wavelength, and frequency. The number of complete waves is a product of the frequency of the wave and the time passed.
$$begin{align*}
v &= lambda f &&(1) \
n &= ft &&(2) \
end{align*}$$

Step 3

3 of 6

As we can see from the first equation, both the wavelength and the frequency are needed to calculate wave speed. One wavelength is defined as a distance between two throughs, crests, or one crest and one through. Since we are given the distance between a trough and an adjacent crest, we need to multiply that by two to find the wavelength:
$$begin{align*}
lambda &= 2d \
&= 2 cdot 3 mathrm{~m} \
&= 6 mathrm{~m}
end{align*}$$

Step 4

4 of 6

Next, the frequency can be found solving the second equation for $f$ dividing it by $t$:
$$begin{align*}
f &= frac{n}{t} \
&= frac{12}{20 mathrm{~s}} \
&= 0.6 mathrm{~Hz}
end{align*}$$

Step 5

5 of 6

Finally, the wavespeed is then the product of the wavelength and frequency above:
$$begin{align*}
v &= lambda f \
&= 6 mathrm{~m} cdot 0.6 mathrm{~Hz} \
&= 3.6 ,frac{text{m}}{text{s}}
end{align*}$$
$$boxed{ v = 3.6 ,frac{text{m}}{text{s}} }$$

Result

6 of 6

$$ v = 3.6 ,frac{text{m}}{text{s}} $$

Exercise 83

Step 1

1 of 2

Suppose that the earthquake is at the distance d and it takes t seconds for the transverse waves to arrive to the shore:

$d = v_{transverse} t = (8.9 km/s) (t)$

For the longitudinal waves:

$d = v_{longitudinal} (t + 68) = (5.1 km/s) (t + 68)$

Therefore:

$(5.1 km/s) (t + 68) = (8.9 km/s) (t)$

$5.1 t + 346.8 = 8.9 t$

$t = dfrac{346.8}{8.9-5.1} = 91.26 s$

$$
d = v_{transverse} t = (8.9 km/s) (91.26) = 812 km
$$

Result

2 of 2

$$
812 km
$$

Exercise 84

Step 1

1 of 4

1., In the case when the amplitudes cancel each other we have: Exercise scan

Step 2

2 of 4

2., In the case where amplitude is doubled we have: Exercise scan

Step 3

3 of 4

3., Resultant of the pulses will be half of the amplitude of the second pulse if the amplitude of the first one is half amplitude of the second one as well. Exercise scan

Result

4 of 4

1., In the first case amplitudes cancel each other.

2., In the second case , amplitude is doubled.

3, Resultant of the pulses will be half of the amplitude of the second pulse if the amplitude of the first one is half amplitude of the second one as well.

Exercise 85

Step 1

1 of 2

$$
lambda = 2cdot 1.5 = 3
$$

$$
v = lambda cdot f = 3cdot 0.3 = 0.9
$$

Result

2 of 2

$$
text{color{#4257b2}0.9 m/s}
$$

Exercise 86

Step 1

1 of 4

Information given in the text are:

$v = 265, mathrm{m/s}$

$l = 63, mathrm{cm} = 0.63, mathrm{m}$

$textit{a.}$, Speed is given by:

$$
v = dfrac{l}{t}
$$

Therefore, $t$ from the previous equation will be:

$$
t = dfrac{l}{v}
$$

$l$ in the case where pulse moves to the string end and then return to the center will be:

$$
d = dfrac{1}{2} cdot 2 cdot 0.63, mathrm{m} = 0.63, mathrm{m}
$$

Now that all of the information are known we can determine $t$:

$$
t = dfrac{0.63, mathrm{m}}{265, mathrm{m/s}}
$$

$$
boxed{t = 2.4 cdot 10^{-3}, mathrm{s}}
$$

Step 2

2 of 4

$textit{b.}$, String will be below its resting location since pulses will be inverted due to the reflection from medium with higher density.

Step 3

3 of 4

$textit{d.}$, Two pulses will meet at $15, mathrm{cm}$ from the opposite end.

Result

4 of 4

$textit{a.}$, $t = 2.4 cdot 10^{-3}, mathrm{s}$

$textit{b.}$, It will be below its restin location.

$textit{c.}$, $15, mathrm{cm}$ from the opposite end

Exercise 87

Step 1

1 of 2

Sketch for each of given four cases, when centers of each of the two wave pulses lie on the dashed line and in that case pulses will overlap, is given above. Exercise scan

Result

2 of 2

When centers of each of the two wave pulses lie on the dashed line and in that case pulses will overlap.

Exercise 88

Step 1

1 of 2

$$
color{#c34632}T = 2pisqrt{dfrac{l}{g}}
$$

Substitute : $l = 1.4$ m and $g = 9.8$ m/s$^2$

$$
T = 2pisqrt{dfrac{1.4text{ m}}{9.8text{ m/s}^2}}approx2.4text{ s}
$$

Result

2 of 2

$$
text{color{#4257b2}2.4text{ s}}
$$

Exercise 89

Step 1

1 of 2

Information given in the text are:

$f = 5.1 cdot 10^{14}, mathrm{Hz}$

$c = 3 cdot 10^{8}, mathrm{m/s}$

Wavelength is given by:

$$
lambda = dfrac{c}{f}
$$

When we put known values into the previous equation we get:

$$
lambda = dfrac{3 cdot 10^{8}, mathrm{m/s}}{5.1 cdot 10^{14}, mathrm{Hz}}
$$

$$
boxed{lambda = 5.9 cdot 10^{7}, mathrm{m}}
$$

Result

2 of 2

$$
lambda = 5.9 cdot 10^{7}, mathrm{m}
$$

Exercise 90

Step 1

1 of 2

$lambda_1 = dfrac{c}{f_1} = dfrac{3.0e8}{1600e3} = 188 m$

$lambda_2 = dfrac{c}{f_2} = dfrac{3.0e8}{550e3} = 545 m$

The wavelengths are between 188 m to 545 m.

$lambda_1 = dfrac{c}{f_1} = dfrac{3.0e8}{108e6} = 2.78 m$

$lambda_2 = dfrac{c}{f_2} = dfrac{3.0e8}{88e6} = 3.41 m$

The wavelengths are between 2.78 m to 3.41 m.

Result

2 of 2

a) between 188 m to 545 m.

b) between 2.78 m to 3.41 m.

Exercise 91

Solution 1

Solution 2

Step 1

1 of 2

They are transverse waves.

Because the water only moves up and down, it does not moves toward the shore.

$T = dfrac{15}{10} = 1.5 s$

$f = dfrac{1}{T} = dfrac{1}{1.5} = 0.67 Hz$

$v = lambda f = (3)*(0.67) = 2.0 m/s$

$$
lambda = dfrac{c}{f} = dfrac{1.8}{0.67} = 2.7 m
$$

Result

2 of 2

a) transverse wave

b) See explanation

c) $1.5 s$

d) $0.67 Hz$

e) $2.0 m/s$

f) $2.7 m$

Step 1

1 of 9

**Given:**
– Time: $t = 15 mathrm{~s}$;
– Number of waves: $n = 10$;
– Wavelength: $lambda = 3 mathrm{~m}$;
– Speed: $v_text{actual} = 1.8 ,frac{text{m}}{text{s}}$;

**Required:**

a) The type of wave;

b) The direction in which the energy spreads;

c) The period $T$;

d) The frequency $f$;

e) The velocity $v$;

f) The wavelength $lambda_text{actual}$;

Step 2

2 of 9

We have an equation that relates the wave speed, wavelength and the frequency. The period can be found by counting how many waves pass in some interval and then dividing the time with the number of waves. The frequency can be found as the reciprocal of the period.
$$begin{align*}
v &= lambda f &&(1) \
T &= frac{t}{n} &&(2) \
f &= frac{1}{T} &&(3)
end{align*}$$

Step 3

3 of 9

**a)** The displacement is in the direction perpendicular to the movement of the wave. Hence, the waves are transverse.

Step 4

4 of 9

**b)** Because the wave is transverse, that means that the energy spreads up and down, not towards the shore.

Step 5

5 of 9

**c)** Plugging in the numbers into the second equation:
$$begin{align*}
T &= frac{t}{n} \
&= frac{15 mathrm{~s}}{10} \
&= 1.5 mathrm{~s}
end{align*}$$
$$boxed{ T = 1.5 mathrm{~s} }$$

Step 6

6 of 9

**d)** The frequency is then the reciprocal of the period above:
$$begin{align*}
f &= frac{1}{T} \
&= frac{1}{1.5 mathrm{~s}} \
&= 0.67 mathrm{~Hz}
end{align*}$$
$$boxed{ f = 0.67 mathrm{~Hz} }$$

Step 7

7 of 9

**e)** The velocity of the waves is the product of the frequency and wavelength:
$$begin{align*}
v &= lambda f \
&= 3 mathrm{~m} cdot 0.67 mathrm{~Hz} \
&= 2.01 ,frac{text{m}}{text{s}}
end{align*}$$
$$boxed{ v = 2.01 ,frac{text{m}}{text{s}} }$$

Step 8

8 of 9

**f)** Using the same equation as in previous step, but solving it for $lambda_text{actual}$ by dividing it by $f$ we can calculate the actual wavelength of the waves:
$$begin{align*}
lambda_text{actual} &= frac{v_text{actual}}{f } \
&= dfrac{1.8 ,frac{text{m}}{text{s}}}{0.67 mathrm{~Hz}} \
&= 2.69 mathrm{~m}
end{align*}$$
$$boxed{ lambda_text{actual} = 2.69 mathrm{~m} }$$

Result

9 of 9

$$begin{align*}
&text{a) See the explanation.} \
&text{b) See the explanation.} \
&text{c) } T = 1.5 mathrm{~s} \
&text{d) } f = 0.67 mathrm{~Hz} \
&text{e) } v = 2.01 ,frac{text{m}}{text{s}} \
&text{f) } lambda_text{actual} = 2.69 mathrm{~m}
end{align*}$$

Exercise 92

Step 1

1 of 2

We have:

$m g = k Delta x$

Solve for k:

$$
k = dfrac{m g}{Delta x} = dfrac{(68)*(9.80)}{(1710 – 540)} = 0.57 N/m
$$

Result

2 of 2

$$
0.57 N/m
$$

Exercise 93

Solution 1

Solution 2

Step 1

1 of 2

This is 1/4 of the wavelength.

$T = (4)*(0.18) = 0.72 s$

$$
f = dfrac{1}{T} = dfrac{1}{0.72} = 1.4 Hz
$$

Result

2 of 2

a) 1/4

b) $0.72 s$

c) $1.4 Hz$

Step 1

1 of 6

**Given:**
– Time: $t = 0.18mathrm{~s}$;

**Required:**

a) The amount of the wavelength;

b) The period $T$;

c) The frequency $f$;

Step 2

2 of 6

The frequency can be found as the reciprocal of the period.
$$begin{align*}
f &= frac{1}{T}
end{align*}$$

Step 3

3 of 6

**a)** One wavelength is defined as a distance between two throughs, crests, or one crest and one through. Since we are told that the water wave goes from the equilibrium level to the crest, that is only one-fourth of the wavelength. It is best seen in the picture below.

![‘slader’](https://slader-solution-uploads.s3.amazonaws.com/18eda662-db10-4aa6-a91e-06c7beccfb90-1650637106745118.png)

Step 4

4 of 6

**b)** The period is defined as the interval of time between two successive occurrences of the same state in an oscillatory phenomenon, or in our case, the time needed for one wavelength. Since $0.18 mathrm{~s}$ is needed for one-quarter of a wavelength, we need to multiply that by four to obtain the period:
$$begin{align*}
T &= 4t \
&= 4 cdot 0.18 mathrm{~s} \
&= 0.78 mathrm{~s}
end{align*}$$
$$boxed{ T = 0.72 mathrm{~s} }$$

Step 5

5 of 6

**c)** Using the equation given with the period calculated in the previous step, we can find the frequency:
$$begin{align*}
f &= frac{1}{T} \
&= frac{1}{0.72 mathrm{~s}} \
&= 1.4 mathrm{~Hz}
end{align*}$$
$$boxed{ f = 1.4 mathrm{~Hz} }$$

Result

6 of 6

$$begin{align*}
&text{a) See the explanation.} \
&text{b) } T = 0.72 mathrm{~s} \
&text{c) } f = 1.4 mathrm{~Hz}
end{align*}$$

Exercise 94

Step 1

1 of 2

Information given in the text are:

$m = 225, mathrm{g} = 0.225, mathrm{kg}$

$x = 0.094, mathrm{m}$

$x = 0.80, mathrm{m}$

First, we will determine spring constant, and since the Newton’s second law gives: $mg = kx$, $k$ will be:

$$
k = dfrac{mg}{x}
$$

When we put known values into the previous equation we get:

$$
k = dfrac{0.225, mathrm{kg}9.81, mathrm{m/s^{2}}}{0.094, mathrm{m}} = boxed{23, mathrm{N/m}}
$$

Next, we will be using conservation of energy:

$$
E_{p} = E_{k}
$$

$$
rightarrow dfrac{1}{2}kx^{2} = dfrac{1}{2}mv^{2}
$$

We can express velocity from the previous equation:

$$
v= sqrt{dfrac{kx^{2}}{m}}
$$

When we put known values into the previous equation we get:

$$
v = sqrt{dfrac{23, mathrm{N/m} cdot (0.080, mathrm{m})^{2}}{0.225, mathrm{kg}}}
$$

$$
boxed{v = 0.81, mathrm{m/s}}
$$

Result

2 of 2

$$
v = 0.81, mathrm{m/s}
$$

Exercise 95

Step 1

1 of 3

$textit{a.}$, Original period of the ride will be:

$$
T = dfrac{1}{f}
$$

When we put known values into the previous equation:

$$
T = dfrac{1}{8, mathrm{dfrac{swings}{60, mathrm{s}}}}
$$

$$
boxed{T = 7.5, mathrm{s}}
$$

$textit{b.}$, New period of the ride will be:

$$
T = dfrac{1}{f}
$$

When we put known values into the previous equation we get:

$$
T = dfrac{1}{dfrac{6, mathrm{swings}}{60, mathrm{s}}}
$$

$$
boxed{T = 10, mathrm{s}}
$$

$textit{c.}$, New frequency will be:

Frequency is given by:

$$
f = dfrac{1}{T}
$$

When we put known values into the previous equation we get:

$$
f = dfrac{1}{1 cdot 10^{-1}, mathrm{s}}
$$

$$
boxed{f = 0.10, mathrm{Hz}}
$$

Step 2

2 of 3

$textit{d.}$, We have to determine $l$, and since period is given by:

$$
T = 2 pi sqrt{dfrac{l}{g}}
$$

$l$ will be:

$$
l = g dfrac{T^{2}}{4 pi^{2}}
$$

When we put known values into the previous equation we get:

$$
l = 9.81, mathrm{m/s^{2}} dfrac{(7.5, mathrm{s})^{2}}{4 pi^{2}}
$$

$$
boxed{l = 14, mathrm{m}}
$$

Result

3 of 3

$textit{a.}$, $T = 7.5, mathrm{s}$

$textit{b.}$, $T = 10, mathrm{s}$

$textit{c.}$, $f = 0.10, mathrm{Hz}$

$textit{d.}$, $l = 14, mathrm{m}$

Exercise 96

Step 1

1 of 2

The equation is:

$T = 2 pi sqrt{dfrac{l}{g}}$

If it loses time it means that its period is more than 1 second and therefore its length is longer than usual. We must make the length of the pendulum shorter.

$T_1 = 2 pi sqrt{dfrac{l_1}{g}} = (2)*(3.1416)*(sqrt{dfrac{0.150}{9.80}}) = 0.77734 s$

$T_2 = T_1 – 0.0400 = 0.77734 – 0.0400 = 0.73734 s$

$T_2 = 2 pi sqrt{dfrac{l_2}{g}}$

$$
==> 0.73734 = (2)*(3.1416)*(sqrt{dfrac{0.150}{9.80}})
$$

$==> l_2 = 0.13496 m$

The change of the length must be:

$$
Delta l = l_1 – l_2 = 0.150 – 0.135 = 0.0150 m
$$

Result

2 of 2

a) shorten

b) $0.0150 m$

Exercise 97

Step 1

1 of 3

Information given in the text are:

$l = 10, mathrm{m}$

$m = 20, mathrm{kg}$

$textit{a.}$, Time taken for swing to reach the peak will half a period:

$$
T_{1} = dfrac{1}{2}T
$$

Since period is given by:

$$
T = 2 pi sqrt{dfrac{l}{g}}
$$

We now have:

$$
begin{align*}
T_{1} &= pi sqrt{dfrac{l}{g}}\
&= pi sqrt{dfrac{10, mathrm{m}}{9.81, mathrm{m/s^{2}}}}\
&= 3.17, mathrm{s}\
end{align*}
$$

$$
boxed{T_{1} = 3.17, mathrm{s}}
$$

Step 2

2 of 3

$textit{b.}$, Since period does not depend on the mass it will be no difference in period.

$textit{c.}$, Kinetic energy will have maximum value at the bottom of the swing.

$textit{d.}$, Potential energy will have maximum value at the top of the swing.

$textit{e.}$, Kinetic energy will have minimum value at the top of the swing.

$textit{f.}$, Potential energy will have minimum value at the bottom of the swing.

Result

3 of 3

$textit{a.}$, $T_{1} = 3.17, mathrm{s}$

$textit{b.}$, There will be no difference in period.

$textit{c.}$, At the bottom of the swing.

$textit{d.}$, At the top of the swing.

$textit{e.}$, At the top of the swing.

$textit{f.}$, At the bottom of the swing.

Exercise 98

Solution 1

Solution 2

Step 1

1 of 2

$k = dfrac{m g}{x} = dfrac{(0.500)*(9.80)}{(0.020)} = 245 N/m$

$m g = k x$

$$
==> m = dfrac{k x}{g} = dfrac{(245)*(0.045)}{9.80} = 1.1 kg
$$

Result

2 of 2

a) $245 N/m$

b) $1.1 kg$

Step 1

1 of 5

**Given:**
– Mass: $m_1 = 500 mathrm{~g}$;
– The stretch: $x_1 = 2 mathrm{~cm}$;

**Required:**

a) The spring constant $k$;

b) The mass $m_2$;

Step 2

2 of 5

We define the elastic force to be the product of the spring constant and the distance the spring is stretched by. The elastic energy is the energy stored in the spring.
$$begin{align*}
F &= kx &&(1) \
PE_text{sp} &= frac{kx^2}{2} &&(2)
end{align*}$$

Step 3

3 of 5

**a)** Solving the first equation for $k$ we divide it by $x$. The force acting on the mass is the force of gravity. Combining that together we have:
$$begin{align*}
k &= frac{F}{ x} \
&= frac{mg}{ x} \
&= dfrac{500 mathrm{~g} cdot 9.81 ,frac{text{m}}{text{s}^2} }{2 mathrm{~cm}} \
&= dfrac{0.5 mathrm{~kg} cdot 9.81 ,frac{text{m}}{text{s}^2} }{0.02 mathrm{~m}} \
&= 245.25 ,frac{text{N}}{text{m}}
end{align*}$$
$$boxed{k = 240 ,frac{text{N}}{text{m}}}$$

Step 4

4 of 5

**b)** Using the same scale, the spring constant remains the same. However, the stretch is now different meaning that the mass has changed. Using the same relationship as in the previous step, where the force of gravity and the elastic force are equal we can solve it for $m$ by dividing it by $g$:
$$begin{align*}
m &= frac{kx}{ g} \
&= dfrac{245.25 ,frac{text{N}}{text{m}} cdot 4.5 mathrm{~cm} }{9.81 ,frac{text{m}}{text{s}^2} } \
&= dfrac{245.25 ,frac{text{N}}{text{m}} cdot 0.045 mathrm{~m} }{9.81 ,frac{text{m}}{text{s}^2}} \
&= 1.125 mathrm{~kg}
end{align*}$$
$$boxed{ m = 1.125 mathrm{~kg} }$$

Result

5 of 5

$$begin{align*}
&text{a) } k = 245.25 ,frac{text{N}}{text{m}} \
&text{b) } m = 1.125 mathrm{~kg}
end{align*}$$

Exercise 99

Step 1

1 of 2

The weight of the load is:

$W = m g = (45)*(9.80) = 441 N$

The force on the each of the springs is:

$F = dfrac{W}{2} = dfrac{441}{2} = 220.5 N$

The spring constant is:

$k = dfrac{F}{x} = dfrac{220.5}{0.010} = 22050 = 2.2 times 10^4 N/m$

$E = (1/2) k x^2$

$E = (1/2) (22050) (0.01)^2$

$$
E = 1.1 J
$$

Result

2 of 2

a) $2.2 times 10^4 N/m$

b) $1.1 J$

Exercise 100

Step 1

1 of 2

$mu = dfrac{m}{L} = dfrac{0.0150}{5.30} = 0.00283 kg/m$

$v = lambda f = (1.20)*(125) = 150 m/s$

We have:

$v = sqrt{dfrac{F_T}{mu}}$

$$
F_T = mu v^2 = (0.00283)*(150)^2 = 63.7 N
$$

Result

2 of 2

$$
63.7 N
$$

Exercise 101

Solution 1

Solution 2

Step 1

1 of 2

$k = dfrac{F}{x} = dfrac{20}{0.5} = 40 N/m$

$E = (1/2) k x^2 = (1/2)*(40)*(0.5)^2 = 5.0 J$

The force of the spring is not constant and it depends on the length of the spring. When the spring is not stretched yet, the force is zero and it increases to final amount of 20 N.

Result

2 of 2

a) 40 N/m

b) 5.0 J

c) See explanation

Step 1

1 of 6

**Given:**
– Force: $F = 20 mathrm{~N}$;
– Stretch: $x = 0.5 mathrm{~m}$;

**Required:**

a) The spring constant $k$;

b) The elastic potential energy $PE_text{sp}$;

c) What happens with the work done to stretch the spring;

Step 2

2 of 6

Step 3

3 of 6

**a)** Solving the first equation for $k$ we divide it by $x$:
$$begin{align*}
k &= frac{F}{ x} \
&= frac{20 mathrm{~N} }{0.5 mathrm{~m}} \
&= 40 ,frac{text{N}}{text{m}}
end{align*}$$
$$boxed{k = 40 ,frac{text{N}}{text{m}}}$$

Step 4

4 of 6

**b)** Plugging in the data into the equation for the energy stored in the spring:
$$begin{align*}
PE_text{sp} &= frac{kx^2}{2} \
&= dfrac{40 ,frac{text{N}}{text{m}} cdot ( 0.5 mathrm{~m})^2 }{2} \
&= 5 mathrm{~J}
end{align*}$$
$$boxed{ PE_text{sp} = 5 mathrm{~J}}$$

Step 5

5 of 6

**c)** As the spring stretches, the greater force needs to be applied, meaning that the force varies with time. Because of that, the work done to stretch the spring is not equal to the force times the distance.

Result

6 of 6

$$begin{align*}
&text{a) } k = 40 ,frac{text{N}}{text{m}} \
&text{b) } PE_text{sp} = 5 mathrm{~J} \
&text{c) See the explanation.}
end{align*}$$

Exercise 102

Step 1

1 of 4

$textit{a.}$,

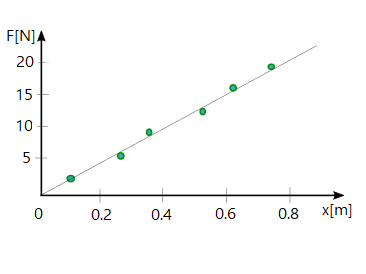
Exercise scan

Step 2

2 of 4

Spring constant can be read from the graph as a slope and slope is $dfrac{Delta F}{Delta x}$:

$Delta F = 15, mathrm{N} – 2.5, mathrm{N} = 12.5, mathrm{N}$

$Delta x = 0.71, mathrm{m} – 0.12, mathrm{m} = 0.59, mathrm{m}$

$$
k = dfrac{12.5, mathrm{N}}{0.59, mathrm{m}} = boxed{21, mathrm{N/m}}
$$

Step 3

3 of 4

Elastic potential energy is area under the line, and area is triangle:

$$
E_{p} = dfrac{1}{2}bh
$$

$h = 10, mathrm{N}$

$b = 0.5, mathrm{m}$

Therefore we have:

$$
E_{p} = dfrac{1}{2} 0.5, mathrm{m} cdot 10, mathrm{N} = boxed{2.5, mathrm{J}}
$$

Result

4 of 4

$textit{b.}$ $k = 21, mathrm{N/m}$

$textit{c.}$, $E_{p} = 2.5, mathrm{J}$

Exercise 103

Step 1

1 of 2

The period of the spring’s oscillation is:

$T = dfrac{d}{v} =dfrac{1.5 m}{5 m/s} = 0.3 s$

The frequency is:

$$
f = dfrac{1}{T} = dfrac{1}{0.3} = 3.3 Hz
$$

Result

2 of 2

$$
3.3 Hz
$$

Exercise 104

Step 1

1 of 2

Newton stated that the best way to explain properties of light during reflection and refraction is by observing light as a beam of particles (photons), on the other hand Huygens stated that the best way is by observing light as a wave.

Refraction and reflection by Newton’s theory are explained as bouncing of particles at different angles when light hits rough surface and at the same angle when it hits smooth surface in the case of reflection and in the case of refraction, when particles enter a new medium they are being attracted by the particles of which the medium is made which causes bending of light.
Refraction and reflection by Huygens’s theory are explained as change in direction of a ray of light as it bounces off the reflective surface in the case of reflection and change in direction of ray of light as it enters a new medium with different optical density.

Both models are accurate when it comes to description of reflection and refraction, therefore, if we choose either Newton’s or Huygen’s theory, we will not make mistake.

Result

2 of 2

Newton stated that reflection is bouncing off of the particles as they hit the surface, in the same angle they hit it when the surface is smooth and at different angles when the surface is rough, on the other hand, Huygens stated that reflection is change in direction of a wave as it hits surface.

Newton stated that refraction is bending of light as it enters a new medium since the particles will be attracted by the particles from which that medium is made and Huygens stated that refraction is change in direction of the wave as it enters a new medium.

Both theories are accurate.

Exercise 105

Step 1

1 of 3

Information given in the text are:

$m = 1400, mathrm{kg}$

$v_{f} = 112, mathrm{m/s}$

$t = 9.8, mathrm{s}$

$textit{a.}$, Kinetic energy is given by:

$$
E_{k} = dfrac{1}{2}m v_{f}^{2}
$$

When we put known values into the previous equation we get:

$$
E_{k} = dfrac{1}{2} 1400, mathrm{kg} cdot (112, mathrm{m/s})^{2}
$$

$$
boxed{E_{k} = 8.8 cdot 10^{6}, mathrm{J}}
$$

$textit{b.}$, Minimum amount of work that has been done by its engine equals kinetic energy that we have previously calculated.

We cannot calculate total amount of work done because engine has to do more work than the work that it has been doing against the friction.

Step 2

2 of 3

$textit{c.}$, Average acceleration is given by:

$$
a_{avg} = dfrac{Delta v}{Delta t}
$$

When we put known values into the previous equation we get:

$$
a_{avg} = dfrac{112, mathrm{m/s}}{9.8, mathrm{s}}
$$

$$
boxed{a_{avg} = 11, mathrm{m/s^{2}}}
$$

Result

3 of 3

$textit{a.}$, $E_{k} = 8.8 cdot 10^{6}, mathrm{J}$

$textit{b.}$, It equals kinetic energy. It cannot be calculated since engine has to do more work than it has been done against the friction.

$textit{c.}$, $a_{avg} = 11, mathrm{m/s^{2}}$

Exercise 106

Solution 1

Solution 2

Step 1

1 of 2

The heat energy in 1 s is:

$Q = P t = (1000)*(1) = 1000 J$

We have:

$Q = m L_v$

Solve for m:

$$
m = dfrac{Q}{L_v} = dfrac{1000}{2.26e6} = 4.4times 10^{-4} kg
$$

Result

2 of 2

$$
4.4 times 10^{-4} kg
$$

Step 1

1 of 6

**Given:**
– Time: $t = 1 mathrm{~s}$;
– Power: $P = 1 mathrm{~kW}$;
– Thermal efficiency: $epsilon = 20%$;
– Heat of vaporization: $H_text v = 2.26 times 10^6 ,frac{text{J}}{text{kg}}$;

**Required:**
– Mass $m$ of the water needed to produce $1 mathrm{~kW}$ of power;

Step 2

2 of 6

To solve this problem, we remember the equation for the heat required to vaporize liquid is given as the product of the mass and the heat of vaporization of the liquid. On the other hand, power is the ratio of energy and time.
$$begin{align*}
Q &= m H_text v &&(1) \
P &= frac{E}{t} &&(2)
end{align*}$$

Step 3

3 of 6

In our case, the energy used to produce power is the energy needed for vaporization. We are told that the engine is only 20 percent efficient. Rewriting the second equation, where the energy is the heat of vaporization, we have:
$$P =0.2 cdot frac{Q}{t} $$

Step 4

4 of 6

Solving that for $Q$, we multiply it by $t$ and divide it by $0.2$:
$$begin{align*}
Q &= frac{Pt}{0.2} \
&= frac{1 mathrm{~kW} cdot 1 mathrm{~s}}{0.2} \
&= frac{1000 mathrm{~W} cdot 1 mathrm{~s}}{0.2} \
&= 5000 mathrm{~J}
end{align*}$$

Step 5

5 of 6

Plugging the data into the first equation and solving it for $m$ by $H_text v$ we can calculate the mass:
$$begin{align*}
m &= frac{Q}{ H_text v } \
&= frac{5000 mathrm{~J}}{2.26 times 10^6 ,frac{text{J}}{text{kg}}} \
&= 2.21 times 10^{-3} mathrm{~kg}
end{align*}$$
$$boxed{ m = 2.21 times 10^{-3} mathrm{~kg} }$$

Result

6 of 6

$$m = 2.21 times 10^{-3} mathrm{~kg} $$

unlock

All Solutions

Page 396: Assessment

Haven't found what you were looking for?

Search for samples, answers to your questions and flashcards