Home Page Textbooks Physics: Principles and Problems Page 828: Assessment

Physics: Principles and Problems

9th Edition

Elliott, Haase, Harper, Herzog, Margaret Zorn, Nelson, Schuler, Zitzewitz

ISBN: 9780078458132

Textbook solutions

All Solutions

Page 828: Assessment

Exercise 44

Step 1

1 of 1

Exercise 45

Step 1

1 of 1

Within the nucleus there are two major forces: electrostatic force coming from positively charged protons which is strongly repulsive and tries to break nucleus apart; and strong nuclear force that binds nucleus together.

Exercise 46

Step 1

1 of 1

The mass defect can be understood as a small difference in mass of the nucleus of the atom and sum of all of the constituent nucleons separately. This tiny difference in mass yields high binding energies in the nucleus because the relativistic mechanics applies to it and relation $E=mc^2$ holds.

Exercise 47

Step 1

1 of 1

In general, large nuclei are more unstable reason being the increasing electrostatic repulsion due to the rising number of protons. However, in theory exist something called a stability island, the region in periodic table where extremely heavy elements with large nuclei exhibit extraordinary long half-lives.

Exercise 48

Step 1

1 of 1

By definition, isotopes are variation of the same element, i.e. they always have the same number of protons but different number of electrons. Therefore, they both have the same number of protons.

Exercise 49

Step 1

1 of 1

Transmutations are defined as changes of one element to another chemical element during some nuclear reaction processes. A typical if not the most common transmutation is $^{235}$U $alpha$-decay to $^{231}$Th.

Exercise 50

Step 1

1 of 1

$alpha$-particles are commonly known as helium nuclei, $beta$-particles are actually electrons and $gamma$-rays are high-energy photons.

Exercise 51

Step 1

1 of 2

In nuclear equations, the two quantities that have to be conserved are the atomic number (a generalized one which can take even negative values) since the charge is implicitly conserved in it and the number of nucleons i.e. the mass number.

Result

2 of 2

Atomic and mass numbers must be conserved.

Exercise 52

Step 1

1 of 1

The sequence of events that must occur so that the chain reaction takes place is that the concentration of fissionable nuclei is large enough so once that the initial fission happens, the released neutrons can cause other fission events with high enough probability.

Exercise 53

Step 1

1 of 1

The role of the moderator in a nuclear reactor is to control the speed, i.e. moderate the motion, of the neutrons participating in the chain reaction keeping it in the range that can induce fission of the desired isotope only. In this way, the reaction remains controllable.

Exercise 54

Step 1

1 of 2

The key is in the binding energy per nucleon of the elements that participate in fusion and fission. The binding energy per nucleon increases very fast till iron, so that helium atom is more stable than two deuterium atoms, for instance. Therefore, the heavier elements are more stable so during the fusion, energy is being released.

Step 2

2 of 2

After iron, the binding energy per nucleon starts to decrease and we have that at the very end of periodic system, lighter elements are more stable than the heavier ones so the breaking of the nuclei releases the energy.

Exercise 55

Step 1

1 of 1

Linear accelerators use the electric field to accelerate particles, which in that case have to be charged. Neutron has zero charge, therefore cannot be accelerated in that particular way.

Exercise 56

Step 1

1 of 3

a) Electrons take part in weak, electromagnetic and gravitational interactions.

Step 2

2 of 3

b) Protons take part in strong, electromagnetic and gravitational interactions.

Step 3

3 of 3

c) Neutrinos take part in weak interaction only.

Exercise 57

Step 1

1 of 1

In positron emission, also known as $beta^+$-decay, a proton decays into a neutron (which remains in the nucleus) while emitting a neutrino and a positron. Therefore, the mass number will remain the same but the atomic number will decrease.

Exercise 58

Step 1

1 of 1

The hypothetical antimatter meteorite would annihilate while interacting with the corresponding matter by particle per particle mechanism. This procedure would create a lot of radiation because each annihilation process by definition releases high energy photons.

Exercise 59

Step 1

1 of 1

Well this is hardly to be true but it is definitely possible scenario since if the iron would be bombarded with the particles high enough to break the iron atoms, yes. However, both fission or fusion of iron would not produce any energy but they are costly processes. This is why in stars, the fusion can create elements up to iron above which the star cannot get any more energy from fusion and collapses and this is one of the reasons why type 2 supernovae happen.

Exercise 60

Step 1

1 of 1

As we can see from the Figure 30-2 the binding energy per nucleon is larger (more negative) for the $^3_2$He than for hydrogen and deuterium therefore this reaction is possible.

Exercise 61

Step 1

1 of 1

Naturally radioactive materials can be found in nature and undergo radioactive decays over the time spontaneously. Artificially radioactive materials do undergo a reactive decay only after being “forced” to do so by collisions with high energy particles.

Exercise 62

Step 1

1 of 1

The reason for this is that the first loop of water serves to moderate the chain reaction and absorb the heat from the uranium rods. It is under a very high pressure which increases its boiling point so it can remove heat in a liquid state from the reactor and brings it the the second water loop (reservoir) which is then allowed to boil resulting in steam that moves turbines.

Exercise 63

Step 1

1 of 3

a) If we take a look at the figure 30-4, we see that the energy of the fission of one uranium nucleus is roughly about 200 MeV. The same figure tells is that the energy produced in a fusion reaction is about 25 MeV.

Step 2

2 of 3

b) One kilogram of hydrogen has almost 250 times more hydrogen nuclei that one kilogram of uranium. Since we need 4 hydrogen nuclei one kilogram of the hydrogen will have 60 times more reactions than one kilogram of uranium. Therefore, simple math gives us that

$$
frac{E_{H}}{E_{U}}=frac{60times 25}{200}=7.5
$$

So one kilogram of hydrogen would give us 7.5 times more energy than one kilogram of uranium.

Step 3

3 of 3

c) The reason for this paradox is that there are almost 250 times more hydrogen atoms than uranium atoms in one kilogram.

Exercise 64

Step 1

1 of 2

Each atom is composed of protons, neutrons, and electrons. By definition, the number of protons is equal to the atomic number and in this case, it is equal to 47. The number of neutrons is given as the difference between the mass number and the atomic number which makes 62 neutrons. Finally, the number of electrons is equal to the number of protons, thus 47.

Result

2 of 2

$n_p=47$, $n_n=62$, $n_e=47$

Exercise 65

Step 1

1 of 3

In this problem, we are asked to write the isotopic symbol of a zinc atom that has 30 protons and 34 neutrons in its nucleus. We know that isotopic symbols are given as
$^A_Ztextrm{X}$
where $Z=n_p$ and $A=n_p+n_n$.

Step 2

2 of 3

In this particular case, we have that the number of protons is 30 so $Z=30$ and number of neutrons is $34$ so $A=30+34=64$. Therefore, the symbol we are looking for is:

$$
^{64}_{30}textrm{Zn}
$$

Result

3 of 3

$$
^{64}_{30}textrm{Zn}
$$

Exercise 66

Step 1

1 of 6

In this problem, we are given a sulfur isotope, $^{32}_{16}$N and its mass. We want to know the mass defect and the corresponding binding energy of the isotope. Finally, we want to know its binding energy per nucleon.

Step 2

2 of 6

The mass defect is defined as the difference between the mass of the atom and the mass of it’s constituents and it can be written as follows

$$
M_d=M-Ztimes(m_p+m_e)-(A-Z)times m_n
$$

Step 3

3 of 6

center{a) In our case we have that }
[M_d=M-16(m_p+m_e)-16m_n=31.97207-16times 1.007825-16times 1.008665]
[boxed{M_d=-0.29177textrm{ u}}]

Step 4

4 of 6

b) The binding energy in MeV is obtained when the mass defect is multiplied by the conversion factor ($1u=931.5$MeV) so that we have

$$
E_B=931.5times M_d=-931.5times 0.29177=boxed{-271.78textrm{ MeV}}
$$

Step 5

5 of 6

c) Finally, the binding energy per nucleon is obtained once we divide the total binding energy by number of nucleons

$$
E_n=frac{E_B}{A}=-frac{271.78}{32}=boxed{-8.49textrm{ MeV}}
$$

Result

6 of 6

$$
textrm{a) }M_d=-0.29177textrm{ u}
$$

$$
textrm{b) }E_B=-271.78textrm{ MeV}
$$

$$
textrm{c) }E_n=-8.49textrm{ MeV}
$$

Exercise 67

Step 1

1 of 6

In this problem, we are given a nitrogen isotope, $^{12}_7$N and its mass. We want to know the binding energy per nucleon and how does it compare with the one from $^{14}_7$N isotope.

Step 2

2 of 6

a) To find the binding energy per nucleon we have to know the mass defect. The mass defect is defined as the difference between the mass of the atom and the mass of it’s constituents and it can be written as follows

$$
M_d=M-Ztimes(m_p+m_e)-(A-Z)times m_n
$$

Step 3

3 of 6

center{ In our case we have that }
[M_d=M-7(m_p+m_e)-5m_n=12.0188-7times 1.007825-5times 1.008665]
[boxed{M_d=-0.0793textrm{ u}}]

Step 4

4 of 6

The binding energy per nucleon is obtained when the mass defect is multiplied by the conversion factor ($1u=931.5$MeV) and divided by the number of nucleons so that we have

$$
E_n=frac{931.5times M_d}{A}=-frac{931.5times 0.0793}{12}=boxed{-6.156textrm{ MeV}}
$$

Step 5

5 of 6

b) Now, we can repeat the entire procedure for the second nitrogen isotope $^{14}_7$N

$$
M_d=M-7(m_p+m_e)-5m_n=14.00307-7times 1.007825-7times 1.008665
$$

$$
M_d=-0.1123textrm{ u}
$$

$$
E_n=frac{931.5times M_d}{A}=-frac{931.5times 0.11236}{12}=boxed{-7.476textrm{ MeV}}
$$

so ti is harder to remove a nucleon from the latter isotope.

Result

6 of 6

$$
textrm{a) }E_n=-6.156textrm{ MeV}
$$

$$
textrm{b) }E_n=-7.476textrm{ MeV}
$$

Exercise 68

Step 1

1 of 3

In this problem, we are given a helium nucleus with the task to determine the Coulomb’s force between the two protons. Coulomb’s law tells us that

$$
F=Kfrac{q_1q_2}{r^2}
$$

Step 2

2 of 3

Now, by simply inserting the given and known values into the above formula we get that

$$
F=9times 10^9timesfrac{1.6^2times 10^{-38}}{2times 10^{-15}}=boxed{58textrm{ N}}
$$

where we have used the fact that $q_1=q_2$.

Result

3 of 3

$$
F=58textrm{ N}
$$

Exercise 69

Step 1

1 of 4

In this problem we are given a helium isotope $^4_2$He and its binding energy. We want to know what is its mass in atomic mass units.

Step 2

2 of 4

In order to find the mass of the given isotope we have to note that the mass defect of a nucleus is given as

$$
M_d=M-Ztimes n_p-(A-Z)times n_n
$$

Then the mass is given by the relation

$$
M=M_d+Ztimes n_p+(A-Z)times n_n
$$

Step 3

3 of 4

On the other hand the mass defect and the binding energy are related as

$$
M_d=frac{E_b}{931.5textrm{ MeV}}
$$

so we can write the following

$$
M=-frac{28.3}{931.5}+2times 1.007825+2times 1.008665=boxed{4.0026textrm{ u}}
$$

Result

4 of 4

$$
M=4.0026textrm{ u}
$$

Exercise 70

Step 1

1 of 4

In this problem, we are asked to write the nuclear equation for $alpha$-decay of the radon isotope $^{222}_{86}$Rn.

Step 2

2 of 4

In order to do so, we are going to write the general $alpha$-decay equation which is given as

$$
^{A}_ZXrightarrow^{A-4}_{Z-2}Y+^4_2alpha
$$

Step 3

3 of 4

From the equation above we see that $Z-2=84$ so the child nucleus is polonium. We can write then

$$
^{222}_{86}textrm{Rn}rightarrow^{218}_{84}textrm{Po}+^4_2alpha
$$

Result

4 of 4

$$
^{222}_{86}textrm{Rn}rightarrow^{218}_{84}textrm{Po}+^4_2alpha
$$

Exercise 71

Step 1

1 of 4

In this problem, we are asked to write the nuclear equation for $beta$-decay of the isotope $^{89}_{36}$Kr.

Step 2

2 of 4

This decay is accompanied by the emission of an electron and an antineutrino and it can be written in the following general form

$$
^A_Ztextrm{X}rightarrow {^textrm{ A}_{(Z+1)}textrm{Y}}+^{textrm{ 0}}_textrm{-1}e+^0_0hatnu
$$

Step 3

3 of 4

center{Now, we can start from the given isotope to obtain that the child nucleus belongs to rubidium}
[^{89}_{36}textrm{Kr}rightarrow ^{89}_{37}textrm{Rb}+e^-+hatnu]

Result

4 of 4

$$
^{89}_{36}textrm{Kr}rightarrow ^{89}_{37}textrm{Rb}+e^-+hatnu
$$

Exercise 72

Step 1

1 of 6

In this problem we are given five different nuclear reactions that we should complete. In order to do so, we are going to use the atomic number and mass number conservation.

Step 2

2 of 6

$$
textrm{a) }^{textrm{225}}_{textrm{ 89}}textrm{Ac}rightarrow^{textrm{4}}_{textrm{2}}textrm{He}+boxed{^{textrm{221}}_{textrm{ 87}}textrm{Fr}}
$$

Step 3

3 of 6

$$
textrm{b) }^{textrm{227}}_{textrm{ 88}}textrm{Ra}rightarrow^{textrm{ 0}}_{textrm{-1}}textrm{e}+boxed{^{textrm{227}}_{textrm{ 89}}textrm{Ac}+, ^{textrm{0}}_{textrm{0}}hatnu}
$$

Step 4

4 of 6

$$
textrm{c) }^{textrm{65}}_{textrm{29}}textrm{Cu}+, ^{textrm{1}}_{textrm{0}}textrm{n}rightarrowboxed{^{textrm{66}}_{textrm{29}}textrm{Cu}}rightarrow^{textrm{1}}_{textrm{1}}textrm{p}+boxed{^{textrm{65}}_{textrm{28}}textrm{Ni}}
$$

Step 5

5 of 6

$$
textrm{d) }^{textrm{235}}_{textrm{92}}textrm{U}+, ^{textrm{1}}_{textrm{0}}textrm{n}rightarrow ^{textrm{96}}_{textrm{40}}textrm{Zr}+3^{textrm{1}}_{textrm{0}}textrm{n}+boxed{^{textrm{137}}_{textrm{ 52}}textrm{Te}}
$$

Result

6 of 6

$$
textrm{a) }^{textrm{225}}_{textrm{ 89}}textrm{Ac}rightarrow^{textrm{4}}_{textrm{2}}textrm{He}+^{textrm{221}}_{textrm{ 87}}textrm{Fr}
$$

$$
textrm{b) }^{textrm{227}}_{textrm{ 88}}textrm{Ra}rightarrow^{textrm{ 0}}_{textrm{-1}}textrm{e}+^{textrm{227}}_{textrm{ 89}}textrm{Ac}+, ^{textrm{0}}_{textrm{0}}hatnu
$$

$$
textrm{c) }^{textrm{65}}_{textrm{29}}textrm{Cu}+, ^{textrm{1}}_{textrm{0}}textrm{n}rightarrow^{textrm{66}}_{textrm{29}}textrm{Cu}rightarrow^{textrm{1}}_{textrm{1}}textrm{p}+^{textrm{65}}_{textrm{28}}textrm{Ni}
$$

Exercise 73

Step 1

1 of 6

In this problem we are given an isotope with a 3-day half-life. We want to know what percent of the original sample is left after a certain period of time.

Step 2

2 of 6

In order to solve this, we are going to use the half-life formula applied to the percentage of the material. we have that

$$
%=(frac{1}{2})^{frac{T}{T_{1/2}}}times 100%
$$

Step 3

3 of 6

a) In the first case $T=6$ days se we can insert the values to get that

$$
%=(frac{1}{2})^{frac{6}{3}}times 100%=25%
$$

Step 4

4 of 6

b) In the second case $T=9$ days se we can insert the values to get that

$$
%=(frac{1}{2})^{frac{9}{3}}times 100%=12.5%
$$

Step 5

5 of 6

c) In the third case $T=12$ days se we can insert the values to get that

$$
%=(frac{1}{2})^{frac{12}{3}}times 100%=6.25%
$$

Result

6 of 6

$$
textrm{a) }%(textrm{6 days})=25%
$$

$$
textrm{b) }%(textrm{9 days})=12.5%
$$

$$
textrm{c) }%(textrm{12 days})=6.25%
$$

Exercise 74

Step 1

1 of 4

In this problem, we are given a radioactive isotope of a three-day half-life which has contaminated the room with 8 times of the allowed radioactivity. We should find the time before the room is decontaminated again.

Step 2

2 of 4

In order to do so, we are going to apply the radioactive decay law which tells us that

$$
A=(frac{1}{2})^{frac{T}{T_{1/2}}}A_0
$$

Step 3

3 of 4

Now, we can insert the parameters given in this problem to have that

$$
frac{1}{8}A_0=(frac{1}{2})^{frac{T}{T_{1/2}}}A_0
$$

So we see that

$$
frac{T}{T_{1/2}}=3
$$

$T=3T_{1/2}=9$
So we should wait at least 9 days before entering the room again.

Result

4 of 4

9 days

Exercise 75

Step 1

1 of 5

In this problem, we are given a boron isotope $^{11}_5$B which is bombarded with protons and after it absorbs the proton it emits a neutron. After that, the obtained isotope decays while emitting a positron. We should describe both processes.

Step 2

2 of 5

a) The first question is which element is formed and since the atomic number of boron is 5 and it absorbs a proton it has to be six so a carbon isotope is formed.

Step 3

3 of 5

b) Since the child nucleus gets one proton but loses one neutron the mass number will remain the same. Then, the nuclear reaction that describes the first process is given as follows

$$
^{textrm{11}}_{textrm{5}}textrm{B}+^{textrm{1}}_{textrm{1}}textrm{p}rightarrow{^{textrm{11}}_{textrm{6}}textrm{C}}+{^{textrm{1}}_{textrm{0}}textrm{n}}
$$

Step 4

4 of 5

c) Now, the newly obtained nucleus undergoes a $beta^+$-decay, where a positron and a neutrino are emitted while a proton is converted to a neutron. Therefore, the mass number still remains the same, but atomic reduces for one. Then, the nuclear reaction that describes the first process is given as follows

$$
^{textrm{11}}_{textrm{6}}textrm{C}rightarrow{^{textrm{11}}_{textrm{5}}textrm{B}}+{^{textrm{ 1}}_{textrm{+1}}textrm{e}}+{^{textrm{0}}_{textrm{0}}nu}
$$

Result

5 of 5

$$
textrm{a) Carbon}
$$

$$
textrm{b) }^{textrm{11}}_{textrm{5}}textrm{B}+^{textrm{1}}_{textrm{1}}textrm{p}rightarrow{^{textrm{11}}_{textrm{6}}textrm{C}}+{^{textrm{1}}_{textrm{0}}textrm{n}}
$$

$$
textrm{c) }^{textrm{11}}_{textrm{6}}textrm{C}rightarrow{^{textrm{11}}_{textrm{5}}textrm{B}}+{^{textrm{ 1}}_{textrm{+1}}textrm{e}}+{^{textrm{0}}_{textrm{0}}nu}
$$

Exercise 76

Step 1

1 of 5

In this problem we are given the energy that was released by the first atomic bomb and the energy released by a single U$_{235}$ nucleus. We want to know the mass of U$_{235}$ used in the bomb.

Step 2

2 of 5

In order to solve this problem, we are going to find first the number of atoms needed to produce such energy. We have that

$$
N=frac{E}{E_a}=frac{20times 5times 10^{12}}{3.21times 10^{-11}}=31.2times 10^{23} textrm{atoms}
$$

Step 3

3 of 5

Our next step is to determine how many moles of substance are given with this many atoms. We have that the number of moles is

$$
n=frac{N}{N_A}=frac{31.2times 10^{23}}{6.022times 10^{23}}=5.17 textrm{mol}
$$

Step 4

4 of 5

Finally, we can use the molar mass of the uranium isotope $M_{U_{235}}=0.235$kg to have that the total mass used is

$$
m=ncdot M_{U_{235}}=5.17times 0.235=boxed{1.22textrm{ kg}}
$$

Result

5 of 5

$$
m=1.22textrm{ kg}
$$

Exercise 77

Step 1

1 of 4

In this problem we are given a step in the fusion reaction where two deuterium nuclei fuse to form a helium isotope $^3_2$He. We want to know what other particle is produced.

Step 2

2 of 4

In order to do so, we shall write the nuclear equation first and then we are solve it for unknown nuclear numbers

$$
^textrm{2}_textrm{1}textrm{H}+^textrm{2}_textrm{1}textrm{H}rightarrow {^textrm{3}_textrm{2}textrm{He}}+{^textrm{A}_textrm{Z}textrm{X}}
$$

Step 3

3 of 4

We see that the atomic number and the mass number of the unknown particle are given as

$$
Z=1+1-2=0
$$

$$
A=2+2-3=1
$$

so we have that the particle is a neutron, $^textrm{1}_textrm{0}textrm{n}$

Result

4 of 4

A neutron, $^textrm{1}_textrm{0}textrm{n}$.

Exercise 78

Step 1

1 of 4

In this problem we are given a polonium isotope of a 103-year half-life. We want to know the time it will take a 100g sample to reduce to 3.1 g only.

Step 2

2 of 4

In order to solve this problem, we are going to start from the law of radioactive decay which says that

$$
m=m_0cdot (frac{1}{2})^{frac{T}{T_{1/2}}}
$$

From which we can express the time T in several simple steps

$$
frac{m_0}{m}= 2^{frac{T}{T_{1/2}}}
$$

$$
logfrac{m_0}{m}=frac{T}{T_{1/2}}log{2}
$$

Step 3

3 of 4

Finally, we have that the time of the decay, $T$ is given by the following relation

$$
T=T_{1/2}frac{log{frac{m_0}{m}}}{log2}=100timesfrac{log{frac{100}{3.1}}}{log2}=boxed{501textrm{years}}
$$

Result

4 of 4

$$
T=501textrm{years}
$$

Exercise 79

Step 1

1 of 3

In this problem we are given a particle composed of three up quarks. We should find its charge.

Step 2

2 of 3

In order to do so, we acknowledge that an up quark has the electric charge of $q_{up}=
frac{2}{3}$e. Therefore, three such quarks would have a total charge given as

$$
Q=3q=3times frac{2}{3}textrm{e}=boxed{2textrm{e}}
$$

Result

3 of 3

$$
Q=2textrm{e}
$$

Exercise 80

Step 1

1 of 3

In this problem we are given a pion that is composed of an up quark and of an anti-down quark. We want the know the charge of the pion.

Step 2

2 of 3

Since the down quark has $q_{down}=-frac{1}{3}$e charge than the anti-down quark will have $q_{anti-down}=frac{1}{3}$e. We can write now

$$
Q=q_{up}+q_{anti-down}=frac{2}{3}e+frac{1}{3}e=boxed{+e}
$$

Result

3 of 3

$$
Q=+e
$$

Exercise 81

Step 1

1 of 5

In this problem we are given different compositions of quarks with a task to find the resulting charge.

Step 2

2 of 5

center{a) Here the particle given is $ubar u$ so we have that }
[u+bar u=frac{2}{3}-frac{2}{3}=0]

Step 3

3 of 5

center{b) Here the particle given is $dbar u$ so we have that }
[d+bar u=-frac{1}{3}e-frac{2}{3}e=-1e]

Step 4

4 of 5

center{c) Here the particle given is $dbar d$ so we have that }
[d+bar d=-frac{1}{3}e+frac{1}{3}e=0]

Result

5 of 5

a) 0

b) -1e

c) 0

Exercise 82

Step 1

1 of 4

In this problem we are give a pair of baryons for which we should determine the total charge based on their quark composition.

Step 2

2 of 4

a) The first one is a neutron that is made of following quarks $ddu$. We have that the total charge is

$$
Q=d+d+u=-frac{1}{3}-frac{1}{3}+frac{2}{3}=0
$$

Step 3

3 of 4

b) The second one is an antiproton that is made of following quarks $bar ubar u bar d$. We have that the total charge is

$$
Q=bar u+bar u+bar d=-frac{2}{3}-frac{2}{3}+frac{1}{3}=-1
$$

Result

4 of 4

a) $Q=0$

b) $Q=-1$

Exercise 83

Step 1

1 of 6

In this problem we are given a proton moving in the Fermi lab synchrotron and we should try to describe it in several steps. We know the diameter of the synchrotron and that protons move at the speed almost equal to the speed of light.

Step 2

2 of 6

a) Our first task is to find the time of a single revolution. By definition, this time is equal to

$$
tau=frac{dpi}{v}=frac{2times 10^3times 3.14}{3times 10^8}=boxed{2.1times 10^{-5}textrm{ s}}
$$

Step 3

3 of 6

b) The next thing we should find is how many revolutions protons need to make to increase their energy from 8 GeV to 400 GeV if in each revolution they get 2.5MeV. We simply get that

$$
N_r=frac{Delta E}{E_r}=frac{(400-8.5)times 10^9}{2.5times 10^6}=boxed{157times 10^3textrm{revolutions}}
$$

Step 4

4 of 6

c) Now, we should find the time needed for protons to reach the aforementioned energy of 400 GeV. We can do so, by multiplying the time needed for one revolution by the total number of revolutions

$$
T=tau times N_r=2.1times 10^{-5}times 157times 10^3=boxed{3.29textrm{ s}}
$$

Step 5

5 of 6

Finally, one should find the total distance covered by the protons during this time. We do that by simply implementing the most famous kinematic formula

$$
v=frac{S}{T}
$$

$$
S=vT=3times 10^8times 3.29=boxed{1times 10^9 textrm{ m}}
$$

Result

6 of 6

$$
textrm{a) }tau=2.1times 10^{-5}textrm{ s}
$$

$$
textrm{b) }N_r=157times 10^3textrm{ revolutions}
$$

$$
textrm{c) }T=3.29textrm{ s}
$$

$$
textrm{d) }S=1times 10^9 textrm{ m}
$$

Exercise 84

Step 1

1 of 3

This is a very, very broad question with very little, almost none of the information needed but let’s try to cover all the cases.

Step 2

2 of 3

There are several things that can influence the curvature of the charged particles in the magnetic field (which is present in bubble chambers). If we are dealing with the same species of particles, i.e. the ones that have the same charge and mass, the path will depend solely on their momentum, i.e. velocities.

Step 3

3 of 3

If we are dealing with several species that have possibly different mass but the same charge and velocity, the curvature will depend on particles’ mass.

Exercise 85

Step 1

1 of 5

Here we are given two nuclei that can absorb $alpha$-particles. We should find child nuclei for each element.

Step 2

2 of 5

The general form of the nuclear equation this processes are about to follow is given as

$$
^textrm{A}_textrm{Z}textrm{X}+{^textrm{4}_textrm{2}}alpharightarrow^textrm{A+4}_textrm{Z+2}textrm{Y}
$$

Step 3

3 of 5

a) In the first case we are given the nitrogen isotope $^{14}_{7}$ that can absorb the alpha particle. From the above equation we see that the new element will have the mass number $A=14+4=18$ and atomic number $Z=7+2=9$ so we deduce that it is fluorine and the nuclear equation is

$$
^textrm{14}_textrm{7}textrm{N}+{^textrm{4}_textrm{2}}alpharightarrow^textrm{18}_textrm{9}textrm{F}
$$

Step 4

4 of 5

b) In the second case we are given the aluminum isotope $^{27}_{13}$ that can absorb the alpha particle. From the above equation we see that the new element will have the mass number $A=27+4=31$ and atomic number $Z=13+2=15$ so we deduce that it is phosphorus and the nuclear equation is

$$
^textrm{27}_textrm{13}textrm{Al}+{^textrm{4}_textrm{2}}alpharightarrow^textrm{31}_textrm{15}textrm{P}
$$

Result

5 of 5

$$
textrm{a) }^textrm{14}_textrm{7}textrm{N}+{^textrm{4}_textrm{2}}alpharightarrow^textrm{18}_textrm{9}textrm{F}
$$

$$
textrm{b) }^textrm{27}_textrm{13}textrm{Al}+{^textrm{4}_textrm{2}}alpharightarrow^textrm{31}_textrm{15}textrm{P}
$$

Exercise 86

Step 1

1 of 4

In this problem we are given a radon sample with a given half-life. We want to know what fraction of the sample will remain after $T=60$h.

Step 2

2 of 4

In order to solve this problem we are going to use the fact that the radioactive decay law tells us that

$$
m=m_0cdotfrac{1}{2^{frac{T}{T_{1/2}}}}
$$

Step 3

3 of 4

By inserting the given values we see that after the given time we have the following fragment of the sample still remaining

$$
m=m_0cdotfrac{1}{2^{frac{60}{15}}}=boxed{frac{1}{16}m_0}
$$

Result

4 of 4

$$
m=frac{1}{16}m_0
$$

Exercise 87

Step 1

1 of 4

In this problem, we are given the simplest fusion reaction, the fusion of a proton and a neutron into a deuterium. We want to write the nuclear reaction for it and find the energy released.

Step 2

2 of 4

The nuclear equation that describes this reaction is very simply in the following line

$$
^textrm{1}_textrm{1}textrm{p}+{^textrm{1}_textrm{0}textrm{n}}{rightarrow}{ ^textrm{2}_textrm{1}textrm{H}}
$$

Step 3

3 of 4

The energy released is found from the mass defect of the reaction multiplied by the energy equivalent of one atomic mass unit. We have that

$$
E=931.5textrm{MeV}cdotDelta M=931.5textrm{MeV}cdot(m_{D}-m_p-m_e)=931.5textrm{MeV}cdot(2.014102-1.007276-1.008665)
$$

$$
E=boxed{-1.71textrm{ MeV}}
$$

which is the energy obtained in this reaction (the final energy is lower than the initial one.)

Result

4 of 4

$$
E=-1.71textrm{ MeV}
$$

Exercise 88

Step 1

1 of 4

In this problem we are given a nucleus of a uranium isotope that decays into a thorium isotope and into an alpha particle of a known kinetic energy. We want to know the kinetic energy of thorium.

Step 2

2 of 4

In order to do so we have to understand that the total kinetic energy that is the sum of the thorium and alpha particle kinetic energy is going to be equal to the mass defect energy of the reaction. We can write that

$$
K=Delta Mcdot 931.5=(232.0372-228.0287-4.0026)times 931.5=5.5 textrm{MeV}
$$

Step 3

3 of 4

Now, the kinetic energy of the thorium nucleus can be obtained as follows

$$
K_{Th}=K-K_{alpha}=5.5-5.3=boxed{0.2textrm{ MeV}}
$$

Result

4 of 4

$$
K_{Th}=0.2textrm{ MeV}
$$

Exercise 89

Step 1

1 of 3

In this problem we are given two gamma rays originating from electron-positron annihilation where the particles are initially at rest. We want to know the momentum of the two gamma rays.

Step 2

2 of 3

Since the initial momentum is zero the momentum of the gamma rays has to be zero, too. Therefore, they are oriented in opposite directions. The magnitude of each momentum is then

$$
p=frac{1}{2}frac{E}{c}=frac{1.02times 10^6times 1.6times 10^{-19}}{2times 3times 10^8}=boxed{272times 10^{-24}, frac{textrm{kg}cdottextrm{m}}{textrm{s}}}
$$

Result

3 of 3

$$
p=272times 10^{-24}, frac{textrm{kg}cdottextrm{m}}{textrm{s}}
$$

Exercise 90

Step 1

1 of 1

The only way that I can think of for three vectors (which gamma rays can be imagined as in this case) of equal magnitude to have net sum of zero is for them to be planar and with 120$^circ$ angle between each one of them.

Exercise scan

Exercise 91

Step 1

1 of 3

In this problem, we are given the energy of one fusion reaction on the sun and the amount of energy the Sun emits per second. We want to know how many fusion reactions are needed for such energy to be emitted each second.

Step 2

2 of 3

In order to do so, we have to divide the energy radiated per second with the energy of a single reaction (which is converted to Joules of course). Therefore, we can write that

$$
N_F=frac{E}{E_F}=frac{4times 10^{26}}{25times 10^6times 1.6times 10^{-19}}=boxed{10^{38}, frac{textrm{fusions}}{textrm{s}}}
$$

Result

3 of 3

$$
N_F=10^{38}, frac{textrm{fusions}}{textrm{s}}
$$

Exercise 92

Solution 1

Solution 2

Step 1

1 of 3

Step 2

2 of 3

According to the above figure, the half life is about 3.3 minutes.

Result

3 of 3

3.3 minutes

Step 1

1 of 8

**Given data**

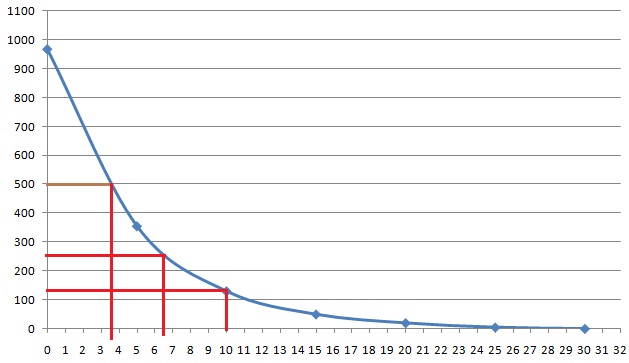
– $mathrm{Count}=[987,375,150,70,40,25,18]$
– $mathrm{Time~[min]}=[0,5,10,15,20,25,30]$

**Objective**

Determine the half-life od the isotope.

Step 2

2 of 8

**Approach**

The half-life of an isotope $T_{1/2}$ is defined as the time in which the number of that isotope in the bulk $N$ decays to the half of the initial number $dfrac{N}{2}$.

Given data is the number of isotopes (Count) at a certain time. By plotting this data and fitting a line, we will be able to read the time it took for isotopes to decay to half of the initial value.

Step 3

3 of 8

Before we start plotting, let’s take into consideration the information about the cosmic rays in the background. Every five minutes we are detecting a count of $20$ due to cosmic rays.

This means that the isotope, in the data we are given, is not alone. Every measurement contains cosmic rays too.

Step 4

4 of 8

Since every measurement is taken at exactly five minutes, just like the count for cosmic rays, this means that each of the count measurements we are given contains $20$ count due to cosmic rays. To avoid this, we can subtract $20$ counts from each measurement we’re given:

$$begin{align}
mathrm{Count-20}=[967,355,130,50,20,5,-2]
end{align}$$

This can be taken to be the count data due to isotope only.

Step 5

5 of 8

We can see in $(1)$ that we got one negative value at the end, but that is no problem since the value of $20$ cosmic rays per 5 mins is only one measure, it could be $15$ at the next $5$ minutes. Taking away $20$ counts is only an approximate measure to reduce the cosmic ray influence.

Now we can plot data ($mathrm{Count-20}$, $mathrm{Time}$).

Step 6

6 of 8

Plotting:

![‘slader’](https://slader-solution-uploads.s3.amazonaws.com/56e0a50c-fe1a-4cbc-ad0b-c0e3a8c4a1d0-1650647448894735.png)

Step 7

7 of 8

To get the half-life, we look at the the time instance at which the number of counts reduced to $dfrac{1}{2}$ of initial value. Since the initial value is $967$, half of that is $485.35$. If we look for this value at the graph, we see that the corresponding time instance is $approx4mathrm{~min}$.

So it took approximately $4mathrm{~min}$ to get to the half of initial value of counts. Thus half-life $T_{1/2}$ is around $boxed{4mathrm{~minutes}}$.

Result

8 of 8

$T_{1/2}approx4mathrm{~min}$

Exercise 93

Step 1

1 of 3

Dark matter is any kind of matter that doesn’t interact with any other force but gravity with regular matter. It is believed to make 85 percent of the total mass of the universe and roughly about 25 percent of the total mass-energy density of the universe.

Step 2

2 of 3

It was introduced initially to explain various anomalies arising in astrophysics and it is believed to be composed of particles yet undiscovered and unpredicted by the standard model of elementary particles. The main effect that was explained by introducing dark matter is the different rotation of large galaxies far from their centers. Basically, one possible explanation was that there exists more mass than actually detected which would influence the rotation. So far, the dark matter theory has passed all the tests of validity but the dark matter remains undetected.

Step 3

3 of 3

It is worth mentioning that exists an alternative theory called MOND (Modified Newtonian Dynamics) managed to be coherent and consistent without introducing extra mass, but rather allowing some physical constants to depend on the distance from the centers of galaxies.

Exercise 94

Step 1

1 of 1

Top quark indeed takes a very special place in the standard model because of its surprisingly large mass that comes from the coupling with the Higgs Boson. It was the last quark discovered and the one that elementary particles physicists predicted to exist 20 years before it was discovered by analogy since they observed that quarks come in pairs. Since they have discovered the bottom quark, they assumed that there has to be a top one to match it. Finally, it was discovered in 1995 in one of the most famous experiments in the Fermilab.

Exercise 95

Step 1

1 of 3

In this problem we are given an electron that enters the magnetic field perpendicularly. We want to know the force acting on this electron by the field.

Step 2

2 of 3

In order to solve this problem we are going to use the equation that defines the magnetic force on the charged particle

$$
F=qvB=1.6times 10^{-19}times 1.7times 10^6times 0.91=boxed{2.48times 10^{-13}textrm{ N}}
$$

Result

3 of 3

$$
F=2.48times 10^{-13}textrm{ N}
$$

Exercise 96

Step 1

1 of 3

In this problem we are given a wire that is moving perpendicularly across the magnetic field at the given velocity. We want to know the magnetic induction of the field.

Step 2

2 of 3

The magnetic induction in a conductor that is moving in a magnetic field can be found in the following way

$$
B=frac{EMF}{lv}=frac{2times 10^{-3}}{0.1times 4}=boxed{5times 10^{-3}textrm{ T}}
$$

Result

3 of 3

$$
B=5times 10^{-3}textrm{ T}
$$

Exercise 97

Step 1

1 of 6

In this problem we are given an electron with a known de Broglie wavelength. We want to find the velocity of the electron and its energy in eV.

Step 2

2 of 6

a) In order to find the velocity of the aforementioned electron we are going to use the de Broglie relation

$$
lambda=frac{h}{mv}
$$

to express the velocity as:

Step 3

3 of 6

$$
v=frac{h}{mlambda}=frac{6.63times 10^{-34}}{9.11times 10^{-31}times 400times 10^{-9}}=boxed{1.82times 10^{3}frac{textrm{m}}{textrm{s}}}
$$

Step 4

4 of 6

center{b) Now, the kinetic energy is given by the well-known equation}
[E=frac{hc}{lambda}]
which after plugging the values and taking that $hc=1240times 10^{-9}$eV$cdot$m becomes

Step 5

5 of 6

$$
E=frac{1240times 10^{-9}}{400times 10^{-9}}
$$

$$
E=boxed{3.1textrm{ eV}}
$$

Result

6 of 6

$$
textrm{a) }v=1.82times 10^{3}frac{textrm{m}}{textrm{s}}
$$

$$
textrm{b) }E=3.1textrm{ eV}
$$

Exercise 98

Step 1

1 of 3

In this problem we are given a photon that hits a hydrogen atom and ionizes it. We want the know what is the kinetic energy of the electron after the ionization.

Step 2

2 of 3

The kinetic energy of the leaving electron will equal the difference between the photon energy and ionization energy of the hydrogen atom. We have that

$$
K=E_{ph}-E_{ion}=14-13.6=boxed{0.4textrm{ eV}}
$$

Result

3 of 3

$$
K=0.4textrm{ eV}
$$

Exercise 99

Step 1

1 of 4

In this problem we are given a silicon diode that is connected in series with a resistor and a power source. We want to know the potential drop across the resistor and the value of its resistance.

Step 2

2 of 4

a) The voltage drop across the resistor in a circuit is equal to the difference of all other potential drops and in our case, we have that

$$
V_R=V_b-V_d=6.67-0.7=boxed{5.97textrm{ V}}
$$

Step 3

3 of 4

b) The actual resistance of the given resistor is to be found now from Ohm’s law directly as

$$
R=frac{V_R}{I_R}=frac{5.97}{137times 10^{-3}}=boxed{43.6, Omega}
$$

Result

4 of 4

$$
V_R=5.97textrm{ V}
$$

$$
R=43.6,Omega
$$

unlock

All Solutions

Page 828: Assessment

Haven't found what you were looking for?

Search for samples, answers to your questions and flashcards