Home Page Textbooks Physics: Principles and Problems Page 452: Assessment

Physics: Principles and Problems

9th Edition

Elliott, Haase, Harper, Herzog, Margaret Zorn, Nelson, Schuler, Zitzewitz

ISBN: 9780078458132

Table of contents

Textbook solutions

All Solutions

Page 452: Assessment

Exercise 24

Step 1

1 of 2

The light has dual nature, the ray model of light, and the wave nature of light. The ray model of light has properties as the constant speed, $c = 3.00 cdot 10^{8} hspace{0.5mm} mathrm{frac{m}{s}}$, and moving in a straight line. However, the wave nature of light has properties like polarization, diffraction, a wavelength $lambda_{0}=frac{c}{f}$, and the Doppler effect. So, we will fill the diagram with these properties.

Step 2

2 of 2

Exercise 25

Step 1

1 of 2

We know that the sound needs an elastic medium to travel. So, the sound cannot travel in a vacuum. Although, the light can travel through a vacuum. We know there is a vacuum in outer space, and yet, we can see sunlight, moonlight, and other light from various stars. So, this is the way how we can know that light travels through a vacuum.

Result

2 of 2

We can see that light travels through a vacuum with sunlight because there is a vacuum in space.

Exercise 26

Step 1

1 of 1

We know that some of the luminous sources are lightbulb or the Sun. The common property for both, a lightbulb and the Sun, is that both of them emit light. So, we can say that the luminous source is the source that emits the light by itself.

However, the illuminated source is for example the Moon. It does not emit light but reflects the light from the Sun. So, we can say that the illuminated source is the source that reflects the light from the luminous source. We can see that light travels through a vacuum with sunlight because there is a vacuum in space.

Exercise 27

Step 1

1 of 2

It is mainly illuminated.

The filament
is luminous; the frosted glass is illuminated.

You barely can see the hot
filament through the frosted glass.

Result

2 of 2

$$
textit{color{#c34632} $See$ $Explanation$}
$$

Exercise 28

Solution 1

Solution 2

Step 1

1 of 1

Ordinary non-luminous classroom objects are reflect the light which falls on them.

When this reflected light reaches our eyes, we see them.

Step 1

1 of 1

The objects in the classroom that are non luminous reflect the light which falls on them. After the light is reflected our eyes sense the reflected light and because of that we can see those objects.

Exercise 29

Step 1

1 of 2

A transparent object is a material
through which light can pass without
distortion.

A translucent object allows
light to pass but distorts the light to the
point where images are not discernable.

An opaque object does not allow light
to pass through.

Result

2 of 2

$$
textit{color{#c34632} $See$ $Explanation$}
$$

Exercise 30

Step 1

1 of 2

From everyday experience, we can observe that when the source of the light is closer to an object, that object is more illuminated. So, the less the distance between the source and the object, the illumination is greater. Also, when is the distance between greater, then the illumination of a surface is lesser. So, we can say that the illumination of a surface is inversely proportional to the distance between the source and the surface.

Also, from everyday experience, we know that when we use a brighter lightbulb, the illumination of a surface is greater. And, when the lightbulb is less bright, the illumination of a surface is lesser. This brightness of a lightbulb is proportional to the luminous flux. So, we can conclude that the illumination of a surface is directly proportional to the luminous flux.
We can see these properties in equation $E= frac{P}{4 pi r^2}$ where $E$ is the illumination, $P$ is the luminous flux, and $r$ is the distance between the light source and the surface.

Result

2 of 2

The illumination of a surface by a light source is directly proportional to the luminous flux and inversely proportional to the distance between the light source and the surface.

Exercise 31

Step 1

1 of 1

Before Galileo, or before the seventeenth century, people thought that the speed of the light approaches infinity. They could not measure the speed, so they believed the light travels instantaneously. But Galileo proved them wrong. He conducted the experiment where he tried to measure the speed of light. His method was not precise, but he successfully concluded that the speed of light is finite, and is too fast to be measured over a small distance.

Exercise 32

Step 1

1 of 2

Diffraction is a phenomenon that appears when a wave comes to an obstacle. In that case, a wave is bending over the obstacle. Also, we saw an example of the diffraction of sound waves and light waves. We are more familiar with the diffraction of a sound wave because a sound wave is in the “macro” dimension, also the obstacle can be in the “macro” dimension. These dimensions (about millimeters and centimeters) are more familiar to us, so we can notice the diffraction of a sound wave. But, diffraction of light waves happens on very small obstacles, smaller than the wavelength. These dimensions are too small for us to notice.

Result

2 of 2

Difference in the value of wavelengths.

Exercise 33

Step 1

1 of 2

In Figure 16-11 we can see the spectrum of light ranges. We are looking for the color with the shortest wavelength. That is the violet, and it has a wavelength of about $lambda = 4.00 cdot 10^{-7} hspace{0.5mm} mathrm{m}$.

Result

2 of 2

Violet $lambda = 4.00 cdot 10^{-7} hspace{0.5mm} mathrm{m}$

Exercise 34

Step 1

1 of 2

In Figure 16-11 we can see the spectrum of visible light. The shortest wavelength of visible light has a violet color [ lambda_{violet}=4.00 cdot 10^{-7} hspace{0.5mm} mathrm{m} ] And the longest wavelength of visible light has a red color [ lambda_{red}=7.00 cdot 10^{-7} hspace{0.5mm} mathrm{m} ] So we can say that the range of visible light is [ framebox[1.1width]{$ therefore lambda_{text{visible light}} in (4.00 cdot 10^{-7} hspace{0.5mm} mathrm{m}, 7.00 cdot 10^{-7} hspace{0.5mm} mathrm{m}) $}]

Result

2 of 2

$$
lambda_{text{visible light}} in (4.00 cdot 10^{-7} hspace{0.5mm} mathrm{m}, 7.00 cdot 10^{-7} hspace{0.5mm} mathrm{m})
$$

Exercise 35

Step 1

1 of 2

White light is a combination of all the
colors, or at least the primary colors.

Result

2 of 2

$$
textit{color{#c34632} $See$ $Explanation$}
$$

Exercise 36

Step 1

1 of 1

When we light some object, if it absorbs almost all of the light, it will appear almost black to us. Or, we can say this, when the body or object reflects almost no light, it appears black.

Exercise 37

Solution 1

Solution 2

Step 1

1 of 1

Only transverse waves can be plane polarized because their vibration is perpendicular to the direction of energy travel – you can therefore have this vibration at different orientations.

Longitudinal waves cannot be plane polarised because the direction of vibration and direction of propagation are the same.

Step 1

1 of 1

Remember from the text what kind of waves exist. There are longitudinal and transverse waves.
1) Transverse waves – medium moves perpendicular to the direction of the wave. (Example: Light waves)
2) Longitudinal waves – medium moves parallel to the direction of the wave. (Example: Sound waves)

In longitudinal waves the displacement of the particles is always in the direction of propagation so because of that they can not be polarized.

Exercise 38

Step 1

1 of 2

We know that galaxy emits light in thegreen region of the light spectrum, so if we observed the wavelength that shifts toward the red light, that means we observe light with a longer wavelength $frac{ lambda_{obs}}{ lambda} > 1$ If we compare this to the equation $frac{ lambda_{obs}}{ lambda}- 1= pm frac{v}{c}$, we can conclude the sign is positive, “+”, so the galaxy is going away from us. Similarly, for a shift toward blue light. In that case, the wavelength of observed light is shorter than the emitted light, so we can write $frac{ lambda_{obs}}{ lambda} < 1$ Now, we are going to compare this with $frac{ lambda_{obs}}{ lambda}- 1= pm frac{v}{c}$, so we can conclude that the sign is negative,"-". In this case, the galaxy is going toward Earth.

Result

2 of 2

For the red shift, the galaxy is going away from Earth.

For the blue shift. the galaxy is going toward to Earth.

Exercise 39

Solution 1

Solution 2

Step 1

1 of 2

$$
color{#c34632}c = lambda f implies lambda = dfrac{c}{f}
$$

$c$ is a universal constant, therefore as $f$ increase $lambda$ decreases

Result

2 of 2

$$
text{color{#4257b2}As frequency increases wavelength of light decreases }
$$

Step 1

1 of 1

Remember the equation for speed of light which includes wavelength and frequency. Wavelength for electromagnetic waves is defined by the equation:
$$c=fcdot lambdatag1$$
We can express the wavelength from it:
$$lambda=frac{c}{f}tag2$$
Keep in mind that the $c$ is a constant value, the speed of light. From here we see that if the frequency increases the wavelength will decrease in it’s value.

Exercise 40

Step 1

1 of 2

Firstly, we are going to observe Screen A. The source of light, the lightbulb, is at the distance of $r_{A}=2.0 hspace{0.5mm} mathrm{m}$. So, we can write the equation for the illuminance $E_{A}=frac{P}{4 pi r_{A}^{2}}$ In the same manner, we can write the equation for Screen B, where the distance between the source of light and the screen is $r_{B}=4.0 hspace{0.5mm} mathrm{m}$, and the equation for the illuminance is $E_{B}=frac{P}{4 pi r_{B}^{2}}$ The luminous flux is the same in the both cases, so we can write

$$
begin{align*}
E_{A}&=frac{P}{4 pi r_{A}^{2}}\
E_{B}&=frac{P}{4 pi r_{B}^{2}}\
frac{E_{B}}{E_{A}}&= frac{ frac{P}{4 pi r_{B}^{2}}}{ frac{P}{4 pi r_{A}^{2}}}\
frac{E_{B}}{E_{A}}&= frac{ r_{A}^{2}}{ r_{B}^{2}}\
frac{E_{B}}{E_{A}}&=left ( frac{ 2.0 hspace{0.5mm} mathrm{m}}{4.0 hspace{0.5mm} mathrm{m}}right)^2\
frac{E_{B}}{E_{A}}&=left( frac{1}{2} right)^2\
frac{E_{B}}{E_{A}}&= frac{1}{4} \
E_{B}&= frac{E_{A}}{4}
end{align*}
$$

The illuminance at Screen B is four times smaller than the illuminance at Screen A.

Result

2 of 2

The illuminance at Screen B is four times smaller than the illuminance at Screen A.

Exercise 41

Step 1

1 of 2

We know that the illuminance is inversely proportional to the distance between the source of light and the illuminated surface. So, in our case, if we double the distance, then the illuminance will be lesser than before.

$a)$ So, the illuminance in the book is not the same.

$b)$ We have already concluded that the illuminance would be lesser. If the initial distance was $r_{before}= 35 hspace{0.5mm} mathrm{cm}$, then the initial illuminance was $E_{before}= frac{P}{4 pi r_{before}^{2}}$ When the distance was doubled, $r_{after} = 2 r_{before} Rightarrow r_{after}=70 hspace{0.5mm} mathrm{cm}$ then the illuminance was $E_{after}= frac{P}{4 pi r_{after}^{2}}$ The luminous flux is the same because it is the same source of light. So, we can write

$$
begin{align*}
E_{before}&=frac{P}{4 pi r_{before}^{2}}\
E_{after}&=frac{P}{4 pi r_{after}^{2}}\
frac{E_{before}}{E_{after}}&= frac{ frac{P}{4 pi r_{before}^{2}}}{ frac{P}{4 pi r_{after}^{2}}}\
frac{E_{before}}{E_{after}}&= frac{ r_{after}^{2}}{ r_{before}^{2}}\
frac{E_{before}}{E_{after}}&= ( frac{2r_{before}}{r_{before}})^{2}\
frac{E_{before}}{E_{after}}&= 2^2\
frac{E_{before}}{E_{after}}&=4\
E_{after}&= frac{E_{before}}{4}
end{align*}
$$

When we doubled the distance, the illuminance was four times lesser than before.

Result

2 of 2

When we doubled the distance, the illuminance was four times lesser than before.

Exercise 42

Step 1

1 of 2

The insides are painted black because
black does not reflect any light, and
thus there is no interference while
observing or photographing objects.

Result

2 of 2

$$
textit{color{#c34632} $See$ $Explanation$}
$$

Exercise 43

Solution 1

Solution 2

Step 1

1 of 1

You can paint them yellow or green since less light needs to be reflected to the eye for the truck to be seen. They are brighter to the eye.

Step 1

1 of 1

The eye is most sensitive to yellow and green light as told from the text. That means in the cases for emergency those would be the **best** colors for vehicle such as fire truck and ambulances. That way people would see them quicker. Combination of those colors would be good as well, which would be some kind of lime color.

Exercise 44

Solution 1

Solution 2

Step 1

1 of 1

No, because the police cars will appear black.

Step 1

1 of 1

If the police cars are dark blue, at night on the yellow, orange-red light those cars would look completely black. That would be good if they want to camouflage their cars at night and go to the crime scene unseen by the criminal for the easier arrest.

Exercise 45

Step 1

1 of 1

We know the relationship between the illuminance and the distance between the light source and an illuminated surface, and that is $E=frac{P}{4 pi d^{2}}$ where $P$ is the luminous flux, $d$ is the distance, and $E$ is the illuminance. We can see that the illuminance and the distance are inversely proportional. If we move the lamp away from the book, the illuminance will be lesser than before.

Exercise 46

Step 1

1 of 1

To give an answer to this question first we will look at the equation $E=frac{P}{4 pi d^{2}}$ where $P$ is the luminous flux, $d$ is the distance, and $E$ is the illuminance. We can see that if we change the distance, there is no change in the luminous flux. That is because the luminous flux is a characteristic of the light source. Also, we know the relationship between the luminous flux and the luminous intensity, and that is the factor $4 pi$, so the luminous intensity is $frac{P}{4 pi}$. We know that there is no change in the luminous flux, so there is no change in the luminous intensity.

Exercise 47

Solution 1

Solution 2

Step 1

1 of 1

Light i scattered from the atmosphere is always polarized. The light coming from the clouds is not polarized. If you rotate the filter, then you can reduce how much polarized light reaches the film.

Step 1

1 of 1

This is a thinking question best for photographers. We can understand it as a physicists because we learned about it in the book. Polarizing filter will block any kind of polarized light and because of that make the sky darker by eliminating any kind of glare or reflections. That way the clouds are much more visible.

Exercise 48

Step 1

1 of 2

We know that when we light some bodies or objects with white light, it will absorb some colors, and the others will be reflected. In this case, the apple absorbs blue and green colors from white light and reflects a red color. This is why we see the apple as red. Similarly with the colored cellophane. Also, sometimes we can use colored cellophane as a filter for a specific color.

$a)$ The red cellophane reflects red light and absorbs the remaining primary colors, blue and green. This is why we see cellophane as red.

$b)$ In this case, we use cellophane as a filter for a red light. The white light is a mix of all primary colors, red, blue, and green. When we light the red cellophane with white light, it only transmits red light.

$c)$ As we said in previous parts, some colors are absorbed. In this case, the red cellophane absorbs the blue and green light.

Result

2 of 2

$a)$ The red cellophane only absorbs red light.

$b)$ The red cellophane only transmits red light.

$c)$ The red cellophane absorbs the blue and green light.

Exercise 49

Step 1

1 of 2

When we put colored cellophane over a fleshlight, it becomes a filter for that specific light. The light in a fleshlight is white, so it is a mix of all colors. So, the cellophane will absorb every other color except its own, and its color will be transmitted. In our case, we have one fleshlight with red cellophane, and that is a red filter. The other fleshlight with green cellophane and it is a green filter. If we direct both fleshlights on the white wall, so they overlap, we have a mix of red and green light. Now we can look at Figure 16-12, and see that the mix of red and green light gives a yellow light. So, on the white wall, we will see yellow color.

Result

2 of 2

We will se yellow color on the wall.

Exercise 50

Solution 1

Solution 2

Step 1

1 of 1

If you shine the flashlight on a white wall, you will see black. No light gets through since the light that’s trying to be transmitted through the filter is absorbed by the second filter.

Step 1

1 of 1

Let’s think about this problem. Remember what is a white light. It’s a light made of every color. Now, what happens when you put a filter? Filter will absorb all the colors except the color the filter is, which means only **that** color can pass through it. So, when the white light passed through the red filter, for example, only light that passed is actually red. Now, when red light meets any other filter except the red one it won’t be able to pass through. In this case the red light **won’t** pass through the green filter. Same would happen if the first filter was red and then the other one green.

Exercise 51

Step 1

1 of 1

Yellow, cyan, and magenta are the primary pigments. We need to get the secondary pigment, blue pigment. To get the secondary pigments from the primary pigments, we need to mix some of the primary pigments. In Figure 16-14, we can see that by mixing the cyan and magenta pigment, we can get the blue pigment.

Exercise 52

Step 1

1 of 2

To find the speed of the car, we need to use the equation [ lambda_{obs} – lambda =- frac{v}{c} lambda] where is $ lambda_{obs}$ the wavelength that the driver saw, and $ lambda $ is the wavelength on the traffic light. The sign is negative, because the driver was approaching to the traffic light. We know that $ lambda_{obs}=545 hspace{0.5mm} mathrm{nm}$, and $ lambda=645 hspace{0.5mm} mathrm{nm}$, so we can calculate the speed of a car
begin{align*}
lambda_{obs}- lambda &=- frac{v}{c} lambda \
frac{v}{c} &= 1- frac{ lambda_{obs}}{ lambda} \
v &= c left(1- frac{ lambda_{obs}}{ lambda}right) \
v &= 3 cdot 10^{8} hspace{0.5mm} mathrm{frac{m}{s}} left(1- frac{ 545 hspace{0.5mm} mathrm{nm} }{ 645 hspace{0.5mm} mathrm{nm}}right) \
v &= 0.465 cdot 10^{8} hspace{0.5mm} mathrm{frac{m}{s}}\
v &= 46.5 cdot 10^{6} hspace{0.5mm} mathrm{frac{m}{s}}
end{align*}
For red light to appear green, the speed of the car should be [ framebox[1.1width]{$ therefore v = 46.5 cdot 10^{6} hspace{0.5mm} mathrm{frac{m}{s}} $}]

Result

2 of 2

$$
v = 46.5 cdot 10^{6} hspace{0.5mm} mathrm{frac{m}{s}}
$$

Exercise 53

Step 1

1 of 2

We have learned how to calculate the illuminance, by using the equation [E=frac{P}{4 pi r^2}] where $P$ is the luminous flux, and $r$ is the distance between the light source and an illuminated surface. In our case, the luminous flux is $P=405 hspace{0.5mm} mathrm{lm}$, and the distance is $r=4.0 hspace{0.5mm} mathrm{m}$. Now, we can write our equation to calculate the illuminance
begin{align*}
E&=frac{P}{4 pi r^{2}}\
E&=frac{405 hspace{0.5mm} mathrm{lm}}{4 pi (4.0 hspace{0.5mm} mathrm{m})^{2}}\
E&=frac{405 hspace{0.5mm} mathrm{lm}}{4 pi 16.0 hspace{0.5mm} mathrm{m}^{2}}\
E&=2.01 hspace{0.5mm} mathrm{lx}
end{align*}
The illumination is [ framebox[1.1width]{$ therefore E=2.0 hspace{0.5mm} mathrm{lx} $}]

Result

2 of 2

$$
E=2.0 hspace{0.5mm} mathrm{lx}
$$

Exercise 54

Step 1

1 of 2

There is a vacuum in the space, and the speed of light in a vacuum is $c=3 cdot 10^{8} hspace{0.5mm} mathrm{frac{m}{s}}$. The light travels from the Moon to Earth for $t=1.28 hspace{0.5mm} mathrm{s}$. So we can calculate the distance between the Moon and Earth as
begin{align*}
d&=c hspace{0.5mm} t\
d&=3 cdot 10^{8} hspace{0.5mm} mathrm{frac{m}{s}} cdot 1.28 hspace{0.5mm} mathrm{s}\
d&=3.84 cdot 10^{8} hspace{0.5mm} mathrm{m}\
d&=3.84 cdot 10^{5} hspace{0.5mm} mathrm{km}\
end{align*}
The distance between the Moon and Earth is [ framebox[1.1width]{$ therefore d=3.84 cdot 10^{5} hspace{0.5mm} mathrm{km} $}]

Result

2 of 2

$$
d=3.84 cdot 10^{5} hspace{0.5mm} mathrm{km}
$$

Exercise 55

Step 1

1 of 2

In this case, our bulb can have three different luminous fluxes, $P_{1}=665 hspace{0.5mm} mathrm{lm}$, $P_{2}=1620 hspace{0.5mm} mathrm{lm}$, or $P_{3}=2285 hspace{0.5mm} mathrm{lm}$. We need to find what is the minimum value of the luminous flux, so the illuminance can be at least $E=175 hspace{0.5mm} mathrm{lx}$. This bulb is positioned $80 hspace{0.5mm} mathrm{cm}$ above a sheet of paper, so that is our distance, [r=80 cdot 10^{-2} hspace{0.5mm} mathrm{m} Rightarrow r=0.8 hspace{0.5mm} mathrm{m} ] We use the equation $E=frac{P}{4 pi r^2}$ to calculate the luminous flux
begin{align*}
E&=frac{P}{4 pi r^{2}}\
P&=4 pi hspace{0.5mm} E hspace{0.5mm} r^{2}\
P&=4 pi cdot 175 hspace{0.5mm} mathrm{lx} cdot (0.8 hspace{0.5mm} mathrm{m})^{2}\
P&=4 pi cdot 175 hspace{0.5mm} mathrm{lx} cdot 0.64 hspace{0.5mm} mathrm{m}^{2}\
P&=1407.43 hspace{0.5mm} mathrm{lm}\
end{align*}
So, we will need the closest upper value of the luminous flux, and that is $P_{2}=1620 hspace{0.5mm} mathrm{lm}$. The minimum setting are going to be [ framebox[1.1width]{$ therefore P=1620 hspace{0.5mm} mathrm{lm} $}]

Result

2 of 2

$$
P=1620 hspace{0.5mm} mathrm{lm}
$$

Exercise 56

Step 1

1 of 4

$a)$ The average increased delay is $t=13 hspace{0.5mm} mathrm{s}$. And within this time, the light travels the $d= c t$ distance, where $c= 3 cdot 10^{8} hspace{0.5mm} mathrm{frac{m}{s}}$ is the speed of light. So the distance that light travels for $13 hspace{0.5mm} mathrm{s}$
begin{align*}
d&= c hspace{0.5mm} t\
d&= 3 cdot 10^{8} hspace{0.5mm} mathrm{frac{m}{s}} cdot 13 hspace{0.5mm} mathrm{s}\
d&= 39 cdot 10^{8} hspace{0.5mm} mathrm{m}
end{align*}
For the time of $13 hspace{0.5mm} mathrm{s}$, the light travels the distance of [ framebox[1.1width]{$ therefore d=39 cdot 10^{8} hspace{0.5mm} mathrm{m} $}]

Step 2

2 of 4

$b)$ It takes $t=42.5 hspace{0.5mm} mathrm{h}$ for Earth to travels the distance of $d=39 cdot 10^{8} hspace{0.5mm} mathrm{m}$ (from part $a)$). Also, we need to find the speed of Earth in $ mathrm{frac{km}{s}}$, so we will write the distance as $d=39 cdot 10^{5} hspace{0.5mm} mathrm{km}$, and the time as $t=1.53 cdot 10^{5} hspace{0.5mm} mathrm{s}$. Now, we can calculate the speed of Earth
begin{align*}
v&=frac{d}{t}\
v&=frac{39 cdot 10^{5} hspace{0.5mm} mathrm{km}}{1.53 cdot 10^{5} hspace{0.5mm} mathrm{s}}\
v&= 25.5 hspace{0.5mm} mathrm{frac{km}{s}}
end{align*}
So, the speed of Earth is [ framebox[1.1width]{$ therefore v=25.5 hspace{0.5mm} mathrm{frac{km}{s}} $}]

Step 3

3 of 4

$c)$ To see if the answer in part $b)$ reasonable, we are going to compare it with the speed of Earth in an orbit of radius, $r=1.5 cdot 10^{8} hspace{0.5mm} mathrm{km}$, in the period 1 year. The speed in part $b)$ is in $mathrm{frac{km}{s}}$, so we need to convert 1 year to seconds $1.0 hspace{0.5mm} mathrm{yr} Rightarrow 1.0 cdot 365 cdot 24 cdot 60 cdot 60 hspace{0.5mm} mathrm{s} Rightarrow 31.54 cdot 10^{6} hspace{0.5mm} mathrm{s}$ Now, we can calculate the speed of Earth

$$
begin{align*}
v&=frac{d}{t}\
v&=frac{2 pi r}{t}\
v&=frac{2 pi 1.5 cdot 10^{8} hspace{0.5mm} mathrm{km} }{31.54 cdot 10^{6} hspace{0.5mm} mathrm{s}}\
v&= 29.9 hspace{0.5mm} mathrm{frac{km}{s}}
end{align*}
$$

If we compare this speed with the speed in part $b)$, we could say the speed in part $b)$ is reasonable.

Result

4 of 4

$a)$ $d=39 cdot 10^{8} hspace{0.5mm} mathrm{m}$

$b)$ $v=25.5 hspace{0.5mm} mathrm{frac{km}{s}}$

$c)$ The speed in part $b)$ is reasonable.

Exercise 57

Step 1

1 of 2

The lamp has a luminous flux of $P_{lamp}=1750 hspace{0.5mm} mathrm{lm}$, and it is positioned at $d_{lamp}=1.25 hspace{0.5mm} mathrm{m} $ away from the sheet of paper. The lightbulb is positioned at $d_{lightbulb}=1.08 hspace{0.5mm} mathrm{m} $ away from the sheet of paper, and the illuminance of lightbulb is same like the illuminance of lamp, so we can write [E_{lamp}=E_{lightbulb}] To calculate the luminous flux of lightbulb, we use the equation $E= frac{P}{4 pi d^2}$
begin{align*}
E_{lamp}&=frac{P_{lamp}}{4 pi d_{lamp}^{2}}\
E_{lightbulb}&=frac{P_{lightbulb}}{4 pi d_{lightbulb}^{2}}\
frac{P_{lightbulb}}{4 pi d_{lightbulb}^{2}}&=frac{P_{lamp}}{4 pi d_{lamp}^{2}}\
P_{lightbulb}&=P_{lamp}frac{d_{lightbulb}^{2}}{d_{lamp}^{2}}\
P_{lightbulb}&=P_{lamp}left( frac{d_{lightbulb}}{d_{lamp}}right)^{2}\
P_{lightbulb}&= 1750 hspace{0.5mm} mathrm{lm} left( frac{ 1.08 hspace{0.5mm} mathrm{m}}{1.25 hspace{0.5mm} mathrm{m}}right )^{2}\
P_{lightbulb}&= 1750 hspace{0.5mm} mathrm{lm} ( 0.86)^{2}\
P_{lightbulb}&= 1306.37 hspace{0.5mm} mathrm{lm}\
end{align*}
The luminous flux of lightbulb is [ framebox[1.1width]{$ therefore P_{lightbulb}= 1306.37 hspace{0.5mm} mathrm{lm} $}]

Result

2 of 2

$$
P_{lightbulb}= 1306.37 hspace{0.5mm} mathrm{lm}
$$

Exercise 58

Step 1

1 of 2

The time for which the light travels from a person to the mirror and back is $t=0.10 hspace{0.5mm} mathrm{s}$. The speed of light in air is approximately $c=3 cdot 10^{8} hspace{0.5mm} mathrm{ frac{m}{s}}$. To calculate the distance that a light travels for time $t$, we use the equation $2d = c t$. In previous equation, the distance is doubled, because the light travels to the mirror and back.
begin{align*}
2d &= c t\
2d &= 3 cdot 10^{8} hspace{0.5mm} mathrm{ frac{m}{s}} cdot 0.10 hspace{0.5mm} mathrm{s}\
2d &= 0.30 cdot 10^{8} hspace{0.5mm} mathrm{ m} /:2\
d &= 0.15 cdot 10^{8} hspace{0.5mm} mathrm{ m}\
d &= 15 cdot 10^{3} hspace{0.5mm} mathrm{ km}\
end{align*}
The mirror would be at the distance of [ framebox[1.1width]{$ therefore d = 15 cdot 10^{3} hspace{0.5mm} mathrm{ km} $}]
The radius of Earth is $R=6738 hspace{0.5mm} mathrm{ km}$, so if we observe the diameter of Earth [D=2R Rightarrow D=13476 hspace{0.5mm} mathrm{ km}]. So, the distance between the mirror and a person should be greater tha the diameter of Earth.
Also, the diameter of Mercury id $4878.3 hspace{0.5mm} mathrm{ km}$, and the distance between the mirror and a person is three times as the diameter of Mercury.

Result

2 of 2

$$
d = 15 cdot 10^{3} hspace{0.5mm} mathrm{ km}
$$

Exercise 59

Step 1

1 of 2

We know that [1 hspace{0.5mm} mathrm{nm} = 10^{-9} hspace{0.5mm} mathrm{m}] So we can convert the wavelength of red light as
begin{align*}
lambda &= 700 hspace{0.5mm} mathrm{nm}\
lambda &= 700 cdot 10^{-9} hspace{0.5mm} mathrm{m}\
lambda &= 0.7 cdot 10^{-6} hspace{0.5mm} mathrm{m}
end{align*}
The wavelength of red light in meters is [ framebox[1.1width]{$ therefore lambda = 0.7 cdot 10^{-6} hspace{0.5mm} mathrm{m} $}]

Result

2 of 2

$$
lambda = 0.7 cdot 10^{-6} hspace{0.5mm} mathrm{m}
$$

Exercise 60

Step 1

1 of 2

To calculate how fast the galaxy is moving relative to Earth, we are using the equation [ lambda_{obs}- lambda= pm frac{v}{c} lambda] The wavelength of hydrogen spectral line is $ lambda= 486 hspace{0.5mm} mathrm{nm}$, and the observed wavelength of hydrogen spectral line is $ lambda_{obs}= 491 hspace{0.5mm} mathrm{nm}$. We know this is the red shift, so the galaxy is moving away from Earth. Because of this, we use a sign $+$ in the previous equation
begin{align*}
lambda_{obs}- lambda&= frac{v}{c} lambda / : lambda\
frac{v}{c} &= frac{ lambda_{obs}}{ lambda} -1 \
v&= c ( frac{ lambda_{obs}}{ lambda} -1)\
v&= 3 cdot 10^{8} hspace{0.5mm} mathrm{frac{m}{s}} ( frac{ 491 hspace{0.5mm} mathrm{nm}}{ 486 hspace{0.5mm} mathrm{nm}} -1)\
v&= 3 cdot 10^{8} hspace{0.5mm} mathrm{frac{m}{s}} (1.01 -1.00)\
v&= 3 cdot 10^{6} hspace{0.5mm} mathrm{frac{m}{s}} \
end{align*}
The speed of the galaxy is [ framebox[1.1width]{$ therefore v= 3 cdot 10^{6} hspace{0.5mm} mathrm{frac{m}{s}} $}]

Result

2 of 2

$$
v= 3 cdot 10^{6} hspace{0.5mm} mathrm{frac{m}{s}}
$$

Exercise 61

Step 1

1 of 1

Yes, the reflected light is polarized. The direction of polarization is parallel to the line joining the eyes of the man.

Exercise 62

Step 1

1 of 1

The sunlight is a natural light, and it is not polarized. When the sunlight falls on the horizontal surface, like a road, it reflects. That reflected rays become polarized in the horizontal direction. If we want to cut the glare from the surface of a road, we need polarized sunglasses with perpendicularly oriented polarization. So, how the reflected rays are horizontally polarized, we need vertically polarized sunglasses.

Exercise 63

Step 1

1 of 2

To find the speed of the galaxy that is moving away from us, we use equation [ lambda_{obs} – lambda = frac{v}{c} lambda] The sign is positive because it is moving away from Earth. Now we know that the wavelength is $ lambda = 434 hspace{0.5mm} mathrm{nm}$, and the observed wavelength is $ lambda = 462 hspace{0.5mm} mathrm{nm}$, and we can calculate the speed
begin{align*}
lambda_{obs}- lambda &= frac{v}{c} lambda \
frac{v}{c} &= frac{ lambda_{obs}}{ lambda} -1 \
v &= c left( frac{ lambda_{obs}}{ lambda} -1right) \
v &= 3 cdot 10^{8} hspace{0.5mm} mathrm{frac{m}{s}} left( frac{ 462 hspace{0.5mm} mathrm{nm} }{ 434 hspace{0.5mm} mathrm{nm}}-1right) \
v &= 0.194 cdot 10^{8} hspace{0.5mm} mathrm{frac{m}{s}}\
v &= 19.4 cdot 10^{6} hspace{0.5mm} mathrm{frac{m}{s}}
end{align*}
The speed of the galaxy is [ framebox[1.1width]{$ therefore v = 19.4 cdot 10^{6} hspace{0.5mm} mathrm{frac{m}{s}} $}]

Result

2 of 2

$$
v = 19.4 cdot 10^{6} hspace{0.5mm} mathrm{frac{m}{s}}
$$

Exercise 64

Step 1

1 of 2

For a galaxy moving away from Earth, the value of the apparent wavelength is greater than realistic value.

Result

2 of 2

greater

Exercise 65

Step 1

1 of 2

The initial situation is that we have two bulbs, that are $d=3.3 hspace{0.5mm} mathrm{m}$ above the ground. The total illuminance for this situation is a superposition of each illuminance
begin{align*}
E&=E_1+E_2\
E&=2E_1\
E&=2 frac{P}{4 pi d^{2}}
end{align*}
If we want to remove one bulb and keep the total illuminance, we have to change the height of the remaining bulb. So, now the bulb is $d^{‘}$ above the ground.
begin{align*}
E&= frac{P}{4 pi d^{‘2}}\
2 frac{P}{4 pi d^{2}} &= frac{P}{4 pi d^{‘2}}\
d^{‘2}&=frac{ d^{2}}{2}\
d^{‘}&= frac{d}{ sqrt{2}}\
d^{‘}&= frac{3.3 hspace{0.5mm} mathrm{m}}{ sqrt{2}}\
d^{‘}&=2.3 hspace{0.5mm} mathrm{m}
end{align*}
The bulb should be at the distance [ framebox[1.1width]{$ therefore d^{‘}=2.3 hspace{0.5mm} mathrm{m} $}]

Result

2 of 2

$$
d^{‘}=2.3 hspace{0.5mm} mathrm{m}
$$

Exercise 66

Solution 1

Solution 2

Step 1

1 of 1

the number of octaves that correspond to the human hearing range:

The octaves are: 20, 40, 80, 160, 320, 640, 1280, 2560, 5120, 10240, 20480
Therefore there are 10 octaves between 20 Hz to 20,000

the number of octaves in the human vision range:

The human vision range is from 4.3e14 Hz to 7.5e14 Hz, therefore there is no octave.

Step 1

1 of 2

Let’s remember what frequencies the human can hear. Only the ones between $20~mathrm{Hz}-20000~mathrm{Hz}$. Octaves in the music are doubling of frequency which is said in the text. The octaves are the following:
$$begin{align*}
&20~mathrm{Hz}\
&40~mathrm{Hz}\
&80~mathrm{Hz}\
&160~mathrm{Hz}\
&320~mathrm{Hz}\
&640~mathrm{Hz}\
&1280~mathrm{Hz}\
&2560~mathrm{Hz}\
&5120~mathrm{Hz}\
&10240~mathrm{Hz}\
&20480~mathrm{Hz}
end{align*}$$
As we can see there are **10** octaves that humans can hear.

Step 2

2 of 2

The human vision has the range from $4.3cdot 10^{14}~mathrm{Hz}$ to $7.5cdot 10^{14}~mathrm{Hz}$. Using this knowledge we can confirm that there is no octave.

Exercise 67

Step 1

1 of 2

One lamp has a luminous intensity of $ frac{P_{1}}{4 pi}=10.0 hspace{0.5mm} mathrm{cd}$, and it is at the distance $d_{1}= 6.0 hspace{0.5mm} mathrm{m}$ from the wall. The other lamp has a luminous intensity of $ frac{P_{2}}{4 pi}=60.0 hspace{0.5mm} mathrm{cd}$, and the illuminances from both lamps are the same, $E_{1}=E_{2}$. We use equation $E=frac{P}{4 pi d^{2}}$ to calculate the distance between the other lamp and the wall
begin{align*}
E_{1}&=E_{2}\
frac{P_{1}}{4 pi d_{1}^{2}}&=frac{P_{2}}{4 pi d_{2}^{2}}\
P_{1} hspace{0.5mm} d_{2}^{2}&=P_{2} hspace{0.5mm} d_{1}^{2}\
4 pi cdot 10.0 hspace{0.75mm} mathrm{cd} hspace{0.75mm} d_{2}^{2}&= 4 pi cdot 60.0 hspace{0.75mm} mathrm{cd} hspace{0.75mm} d_{1}^{2}\
d_{2}^{2}&= 6.0 hspace{0.5mm} d_{1}^{2}\
d_{2}&= sqrt{6.0} d_{1}\
d_{2}&= sqrt{6.0} 6.0 hspace{0.5mm} mathrm{m}\
d_{2}&= 14.7 hspace{0.5mm} mathrm{m}
end{align*}
The other lamp should be at the distance [ framebox[1.1width]{$ therefore d_{2}= 14.7 hspace{0.5mm} mathrm{m} $}]

Result

2 of 2

$$
d_{2}= 14.7 hspace{0.5mm} mathrm{m}
$$

Exercise 68

Step 1

1 of 2

We know that the speed of light in the air is $c= 3.0 cdot 10^{8} hspace{0.5mm} mathrm{frac{m}{s}}$, and the speed of sound in the air is $v=343 hspace{0.5mm} mathrm{frac{m}{s}}$. If there is a lightning strike $l=1.6 hspace{0.5mm} mathrm{km}$ away from us, the light travles to us almost instantly $t_{light}= frac{l}{c} Rightarrow t_{light}= frac{1.6 cdot 10^{3} hspace{0.5mm} mathrm{m}}{3.0 cdot 10^{8} hspace{0.5mm} mathrm{frac{m}{s}}} Rightarrow t_{light}= 5.3 hspace{0.5mm} mathrm{ mu s}$ But the thunder is a sound that we hear, and it travels $t_{sound}= frac{l}{v} Rightarrow t_{sound}= frac{1.6 cdot 10^{3} hspace{0.5mm} mathrm{m}}{343 hspace{0.5mm} mathrm{frac{m}{s}}} Rightarrow t_{sound}= 4.7 hspace{0.5mm} mathrm{s}$ So, the sound travels almost for $5 hspace{0.5mm} mathrm{s}$.

Result

2 of 2

The speed of sound is lesser than the speed of light.

Exercise 69

Solution 1

Solution 2

Step 1

1 of 2

The speed of the edges is:

$v = dfrac{(3.1416)*(1.4e9)}{(25)*(24)*(60)*(60)} = 2036 m/s$

The wavelength is:

$lambda = dfrac{c}{f} = dfrac{3e8}{6.16e14} = 4.87013 times 10^{-7} m$

one edge of Sun is moving away from Earth:

$lambda_a = lambda (1 + dfrac{v}{c}) = (4.87013 times 10^{-7}) (1 + dfrac{2036}{3.0e8}) = 4.870163e-7 m$

one edge of Sun is moving toward Earth:

$lambda_t = lambda (1 – dfrac{v}{c}) = (4.87013 times 10^{-7}) (1 – dfrac{2036}{3.0e8}) = 4.870096818e-7 m$

The change in wavelength is:

$$
Delta lambda = lambda_a – lambda_t = (4.870163e-7) – (4.870096818e-7) = 6.62 times 10^{-12} m
$$

Result

2 of 2

$$
6.62 times 10^{-12} m
$$

Step 1

1 of 6

This is a complex problem in which we will need to calculate the speed of the suns edges. Which can be done easily because we know the time it takes for sun to rotate once as well as the suns diameter. That can be done using equation for speed:
$$v=frac{s}{t}tag1$$
From there we will calculate the wavelength of light emitted by the hydrogen. We know the speed of light and are given the information about frequency of those light waves. Equation is:
$$lambda=frac{v}{f}tag2$$
Each respective wavelength (away and towards the Earth) are shown in the next two equations:
$$lambda_{away}=lambdacdotbigg(1+frac{v}{c}bigg)tag3$$
and
$$lambda_{towards}=lambdacdotbigg(1-frac{v}{c}bigg)tag4$$

Step 2

2 of 6

The time for sun to rotate once is given in the $days$ units which we are going to convert into the seconds.
$$t=25~mathrm{days}=2160000~mathrm{s}$$
Also we need to find the circumference of the sun using the diameter:
$$begin{align*}
s&=pi cdot d\
&= 3.14cdot 1.4cdot 10^9~mathrm{m}\
&=4396cdot 10^6~mathrm{m}
end{align*}$$
Let’s start from the beginning we need to calculate the speed of suns edge, the $v$ from equation (1):
$$begin{align*}
v&=frac{s}{t}\
&=frac{4396cdot 10^6~mathrm{m}}{2160000~mathrm{s}}\
&=2036~mathrm{frac{m}{s}}
end{align*}$$

Step 3

3 of 6

Now let’s find the wavelength using the given informations and equation (2):
$$begin{align*}
lambda&=frac{v}{f}\
&= frac{3cdot cancel{10^8}~mathrm{frac{m}{cancel{s}}}}{6.16cdot 10^{cancel{14}}~mathrm{cancel{Hz}}}\
&=4.87013cdot 10^{-7}~mathrm{m}
end{align*}$$

Step 4

4 of 6

Now that we have done those steps we can start calculating the wavelength of the edges that go towards the Earth and the opposite one, going away.
$$begin{align*}
lambda_{away}&=lambdacdotbigg(1+frac{v}{c}bigg)\
&=4.87013cdot 10^{-7}~mathrm{m} cdotbigg(1+frac{2036~mathrm{cancel{frac{m}{s}}}}{3cdot 10^8~mathrm{cancel{frac{m}{{s}}}}}bigg)\
&=4.870163cdot 10^{-7}~mathrm{m}
end{align*}$$
And now the other one:
$$begin{align*}
lambda_{towards}&=lambdacdotbigg(1-frac{v}{c}bigg)\
&=4.87013cdot 10^{-7}~mathrm{m} cdotbigg(1-frac{2036~mathrm{cancel{frac{m}{s}}}}{3cdot 10^8~mathrm{cancel{frac{m}{{s}}}}}bigg)\
&=4.87009682cdot 10^{-7}~mathrm{m}
end{align*}$$

Step 5

5 of 6

Final step is going to be the subtraction of those two wavelengths:
$$begin{align*}
Delta lambda&= lambda_{away}-lambda_{towards}\
&=4.87016300cdot 10^{-7}~mathrm{m} – 4.87009682cdot 10^{-7}~mathrm{m}\
&= 0.00006618cdot 10^{-7}~mathrm{m}\
&=boxed{6.62cdot 10^{-12}~mathrm{m}}
end{align*}$$
And that is the observed change in wavelength.

Result

6 of 6

$Delta lambda=6.62cdot 10^{-12}~mathrm{m}$

Exercise 70

Solution 1

Solution 2

Step 1

1 of 1

The problem was that the speed of light is too fast; light takes about 0.000005 seconds to travel that there’s no way the interval could have been measured using the tools Galileo had.

Step 1

1 of 1

Remember the value for speed of light. It’s $300000000~mathrm{frac{m}{s}}$. Galileo wanted to measure the speed of light in one simple method, his assistant would open the lanterns from the top of one hill while Galileo measures the time the light needs to reach him. The problem was that he couldn’t measure it because it was too fast. They progressively increased the distance, but with the same result. They even tried to measure it in heartbeats instead of seconds, because there is almost two heartbeats in one second. They didn’t have proper equipment for measuring the speed of light. Also their distance was really small for the light, because it needed much less than one second to pass it which was the best unit they could measure it in $16^{th}-17^{th}$ century.

Exercise 71

Step 1

1 of 4

The luminous intensity is $frac{P}{4 pi}=110 hspace{0.5mm} mathrm{cd}$, where $P$ is a luminous flux. Our initial distance is $1.0 hspace{0.5mm} mathrm{m}$, and our final distance is $7.0 hspace{0.5mm} mathrm{m}$. We are going to use the equation $E= frac{P}{4 pi d^{2} }$ to draw the graph.

Step 2

2 of 4

Step 3

3 of 4

$a)$ We can see that the graph is decreasing. Also, we can notice that the graph is concave. This is the graph of function $y(x)=frac{C}{x^{2}}$, where $C$ is constant.

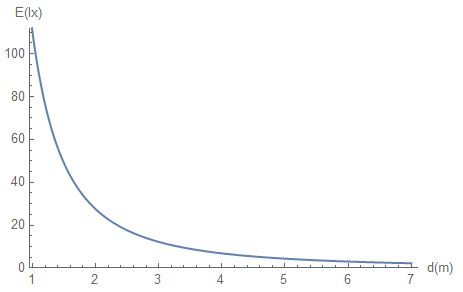
$b)$The information from part $a)$help us to conclude the relationship between illuminance ($y$-axis) and distance ($x$-axis). The illuminance is on the $y$-axis, and the distance is on the $x$-axis. So the relationship between illuminance and distance if $E=frac{C}{d^{2}}$.

Result

4 of 4

$a)$ The shape of graph is concave and decreasing.

$b)$ The relationship between illuminance and distance is $E=frac{C}{d^2}$

Exercise 72

Step 1

1 of 2

Natural light, like sunlight or light from a bulb, is not polarized. However, it can become polarized by two methods, polarized by filtering, and by reflection. We can let the polarized light through a polarization filter, and if their axes are perpendicular, the light does not pass through. If their axes are parallel, then the light passes through. In our case, the sunlight is polarized by reflection on the glass-covered walls. To protect our eyes from reflected rays of sunlight, we can use polarizing glasses. They dim the light and help us to see the road.

Result

2 of 2

The polarizing glasses would help us.

Exercise 73

Step 1

1 of 2

Before the 17th century, before Galileo, most people thought that light travels with an unlimited speed. However, that is not surprising, because the speed of light was undetectable at that time. People did not have convenient instruments for the detection of light speed. But, Galileo made the revolutionary conclusion. He realized that the light speed is not infinity, but it is enormous. Galileo made the experiment with lanterns. He, and his assistant, took lanterns, and climb on the two hills. Firstly, the assistant would lift the shutter on his lantern, and when Galileo would say this, he would lift the shutter on his lantern. He measured the time that took for his assistant to notice the light. He concluded that the light speed is not unlimited, only extraordinarily rapid. Galileo’s work was an inspiration for many others to try to measure the speed of light.

About 50 years later, Danish astronomer, Ole Roemer was the first to measure the light speed. He observed Jupiter’s moon, Io, and its patter of the eclipse. After observation for a longer period, he could predict when the next eclipse of Io would occur. With his calculation and measurement, he came to the first measured speed of light, and that was about $220 000 hspace{0.5mm} mathrm{frac{km}{s}}$.

After Roemer, in the 18th century, James Bradley was studying the aberration of light by looking at the distant star, and his calculation of the speed of light is $301 000 hspace{0.5mm} mathrm{frac{km}{s}}$. After Bradley, in the 19th century, Fizeau and Foucault, with their methods, toothed wheel, and rotating mirror, measured the speed of light. Fizeau got the speed of $315 000 hspace{0.5mm} mathrm{frac{km}{s}}$, and Foucault got $298 000 hspace{0.5mm} mathrm{frac{km}{s}}$. We can see that Bradley and Foucault got a very close measured value to the exact value of the speed of light.

In 1926., Albert Michelson, using the method of an eight-sided rotating mirror, got the most precise value of the speed of light until then. Also, he was the first American who got the Nobel prize. He measured $299 796 hspace{0.5mm} mathrm{frac{km}{s}}$.
Now, in modern times, we use sophisticated techniques to measure the speed of light. The precise value of the speed of light is equal to $299 792 458 hspace{0.5mm} mathrm{frac{m}{s}}$.

Result

2 of 2

Galileo conclude that the speed of light is not unlimited.

Ole Roemer measured $220000 hspace{0.5mm} mathrm{km/s}$.

James Bradley measured $301 000 hspace{0.5mm} mathrm{km/s}$.

Fizeau measured $315 000 hspace{0.5mm} mathrm{km/s}$.

Foucault measured $298 000 hspace{0.5mm} mathrm{km/s}$.

Albert Michelson measured $299 796 hspace{0.5mm} mathrm{km/s}$.

Modern times $299792458 hspace{0.5mm} mathrm{m/s}$

Exercise 74

Step 1

1 of 2

We could say that $1 hspace{0.5mm} mathrm{cd}$ is the luminous intensity of a candle in any direction. This is the origin of the unit’s name “candela”. To understand what $1 hspace{0.5mm} mathrm{cd}$, we could image some point-source of light of luminous flux $P=12.57 hspace{0.5mm} mathrm{lm}$, because $1 hspace{0.5mm} mathrm{cd} = frac{P}{4 pi}$ where $4 pi$ is steradian, $mathrm{sr}$, a solid angle. The latest definition of luminous intensity use the luminous efficacy of monochromatic radiation of frequency, $K_{cd}$, hyperfine transition frequency of Cs, $Delta v_{Cs}$, Planck constant, $h$, and speed of light in vacuum, $c$. With these information you can get the precise value of $1 hspace{0.5mm} mathrm{cd}$.

Result

2 of 2

$1 hspace{0.5mm} mathrm{cd}$ is the luminous intensity of one candle in any given direction.

Exercise 75

Step 1

1 of 5

The mass of an object is $m=2.0 hspace{0.5mm} mathrm{kg}$, and it is attached to a string of length $r=1.5 hspace{0.5mm} mathrm{m}$. This object had constant speed of $v=12 hspace{0.5mm} mathrm{frac{m}{s}}$. On the diagram below, we can see the forces in the position A, at the top of objects path, and in the position B, at the bottom of objects path. In both cases the sum of these forces, the tension force and the gravity force, has the role of centripetal force, so we can write $Sigma bar{F}= bar{F}_{c}$ where $bar{F}_{c}$ is a centripetal force, $F_{c}= frac{m v^{2}}{r}$.

Step 2

2 of 5

Step 3

3 of 5

$a)$ The tension force in the position B can be found with an equation [ Sigma bar{F}= bar{F}_{c}] Where $Sigma bar{F}= m bar{g}+ bar{T}$. We are going to write these vectors like $ m bar{g} = – mg hat{y}$, $ bar{T} = T hat{y}$, and $ bar{F}_{c}= F_{c} hat{y}$. So now, we have
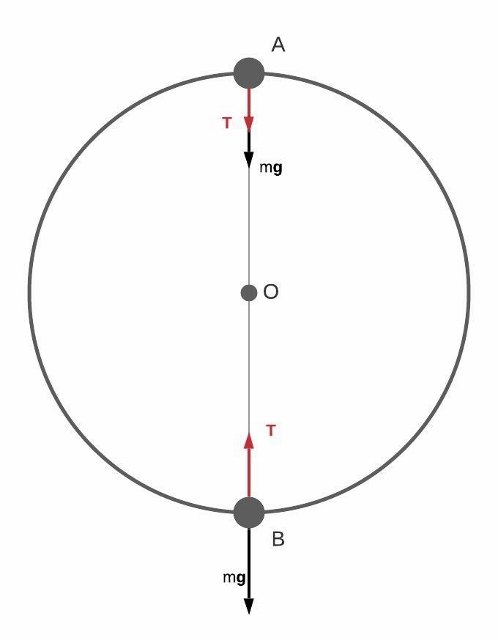
begin{align*}
T-mg&= frac{m v^{2}}{r}\
T&= mg+ frac{m v^{2}}{r}\
T&= 2.0 hspace{0.5mm} mathrm{kg} cdot 9.8 hspace{0.5mm} mathrm{ frac{m}{s^2}} + frac{2.0 hspace{0.5mm} mathrm{kg} (12 hspace{0.5mm} mathrm{frac{m}{s}})^{2}}{1.5 hspace{0.5mm} mathrm{m}}\
T&= 19.6 hspace{0.5mm} mathrm{ N} + frac{2.0 hspace{0.5mm} mathrm{kg} 144 hspace{0.5mm} mathrm{frac{m}{s}}^{2}}{1.5 hspace{0.5mm} mathrm{m}}\
T&= 19.6 hspace{0.5mm} mathrm{ N} + 192 hspace{0.5mm} mathrm{ N} \
T&= 211.6 hspace{0.5mm} mathrm{ N} \
end{align*}
The tension force at the top of the objects path is [ framebox[1.1width]{$ therefore T= 211.6 hspace{0.5mm} mathrm{ N} $}]

Step 4

4 of 5

$b)$ Same as in part $a)$, we have [ Sigma bar{F}= bar{F}_{c}] Where $Sigma bar{F}= m bar{g}+ bar{T}$. We are going to write these vectors like $ m bar{g} = – mg hat{y}$, $ bar{T} =- T hat{y}$, and $ bar{F}_{c}= – F_{c} hat{y}$. Now, we have
begin{align*}
T+mg&= frac{m v^{2}}{r}\
T&= frac{m v^{2}}{r} – mg\
T&= frac{2.0 hspace{0.5mm} mathrm{kg} (12 hspace{0.5mm} mathrm{frac{m}{s}})^{2}}{1.5 hspace{0.5mm} mathrm{m}} – 2.0 hspace{0.5mm} mathrm{kg} cdot 9.8 hspace{0.5mm} mathrm{ frac{m}{s^2}} \
T&= frac{2.0 hspace{0.5mm} mathrm{kg} 144 hspace{0.5mm} mathrm{frac{m}{s}}^{2}}{1.5 hspace{0.5mm} mathrm{m}} – 19.6 hspace{0.5mm} mathrm{ N}\
T&= 192 hspace{0.5mm} mathrm{ N} -19.6 hspace{0.5mm} mathrm{ N} \
T&= 172.4 hspace{0.5mm} mathrm{ N} \
end{align*}
The tension force at the top of the objects path is [ framebox[1.1width]{$ therefore T= 172.4 hspace{0.5mm} mathrm{ N} $}]

Result

5 of 5

$a)$ $T= 211.6 hspace{0.5mm} mathrm{N}$

$b)$ $T= 172.4 hspace{0.5mm} mathrm{N}$

Exercise 76

Step 1

1 of 2

The speed of the space probe in the perpendicular direction should be:

$u = v tan(30) = (125)*tan(30.0) = 72.169 kg.m/s$

The rocket equation is:

$u = V_{gas} Ln(dfrac{M}{M-m_{gas}})$

$72.169 = (3200) Ln(dfrac{7600}{7600-m_{gas}})$

Solve for $M_{gas}$:

$$
M_{gas} = 169 kg
$$

Result

2 of 2

$$
169 kg
$$

Exercise 77

Step 1

1 of 2

We have a string of length $l= 60.0 hspace{0.5mm} mathrm{cm}$, and if it is plucked in the middle, we have situation like on diagram below. From this diagram, we can see the shape of the wave, and it is called first harmonic. For first harmonic, the relation between a wavelength and a length of string is $ lambda = 2l$. We use equation [ f = frac{v}{ lambda}] where $f=440 hspace{0.5mm} mathrm{Hz}$ is frequency of the note. Now, we can calculate the speed of the waves
begin{align*}
f&= frac{v}{ lambda} \
v&= f lambda \
v&= 2 hspace{0.5mm} f hspace{0.5mm} l \
v&= 2 cdot 440 hspace{0.5mm} mathrm{Hz} cdot 60.0 cdot 10^{-2} hspace{0.5mm} mathrm{m} \
v&= 528 hspace{0.5mm} mathrm{frac{m}{s}}
end{align*}
The speed of the waves on the string is [ framebox[1.1width]{$ therefore v= 528 hspace{0.5mm} mathrm{frac{m}{s}} $}]

Result

2 of 2

$$
v= 528 hspace{0.5mm} mathrm{frac{m}{s}}
$$

Exercise 78

Step 1

1 of 2

From Table 15-1, in Chapter 15, we know that the speed of sound in water at $25 hspace{0.5mm} textdegree mathrm{C}$, which is $v= 1493 hspace{0.5mm} mathrm{m/s}$. To find the wavelength of a sound, we use the equation [f= frac{ v}{ lambda}] where $f= 17,000 hspace{0.5mm} mathrm{Hz}$ is a frequency of a sound. Now, we can calculate the wavelength
begin{align*}
f&= frac{v}{ lambda} \
lambda &= frac{v}{f}\
lambda &= frac{1493 hspace{0.5mm} mathrm{m/s}}{17 000 hspace{0.5mm} mathrm{Hz}}\
lambda &= 87.8 hspace{0.5mm} mathrm{mm}
end{align*}
The wavelength of a sound in water at $25 hspace{0.5mm} textdegree mathrm{C}$ is [ framebox[1.1width]{$ therefore lambda = 87.8 hspace{0.5mm} mathrm{mm} $}]

Result

2 of 2

$$
lambda = 87.8 hspace{0.5mm} mathrm{mm}
$$

unlock

All Solutions

Page 452: Assessment

Haven't found what you were looking for?

Search for samples, answers to your questions and flashcards