We are told that charge on the electroscope is
$q = 7.5 cdot 10^{-11} ~mathrm{C}$
and we know that total charge $q$ on any object must be equal to a product of a whole number $N$ and elementary charge $e$. This is due to a fact that elementary charge is the least amount of charge on any object and any other charge on an object is equal to:

$$
q = N e
$$

Since charge on the electroscope is positive, we conclude that number $N$, in this case, represents the deficit of electrons – in other words number $N$ represents the number of protons carrying the charge on the electroscope and is calculated as:

$$
begin{align*}
N &= dfrac{q}{e} \
N &= dfrac{ 7.5 cdot 10^{-11} ~mathrm{C} }{ 1.6 cdot 10^{-19} ~mathrm{C} }
end{align*}
$$

$$
boxed{N = 468750000}
$$

$$
D)~ N approx 4.7 cdot 10^8
$$

Electric force $F$ between charges $q_A$ and $q_B$ at a distance $r$ from each other is given as:

$$
begin{equation}
F = dfrac{k q_A q_B}{r^2}
end{equation}
$$

where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.

In this problem we are given two charged particles. Charge $q_1$ on one of the particles is known and is equal to $q_1 = 5 cdot 10^{-9} ~mathrm{ C}$, while charge $q_2$ on the other particle must be calculated. Charges are at a distance of $r = 4 ~mathrm{cm} = 0.04 ~mathrm{m}$ and force between the two charges is
$F = 8.4 cdot 10^{-5} ~mathrm{N}$.
We can plug in this data into equation $(1)$, a general equation for force between the two charges and find that the force between these two charges is equal to:

$$
begin{align*}
F &= dfrac{k q_A q_B }{r^2} \
text{apply the equation for our problem:}\
F &= dfrac{k q_1 cdot q_2 }{r^2} \
text{express $q_2$ from the equation above}\
F r^2 &= k q_1 q_2 \
q_2 &= dfrac{F r^2}{k q_1 } \
%
%
q_2 &= dfrac{ 8.4 cdot 10^{-5} ~mathrm{N} cdot (0.04 ~mathrm{m} )^2 }{ 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} cdot 5 cdot 10^{-9} ~mathrm{ C} }
end{align*}
$$

$$
boxed{ q_2 = 2.9866 cdot 10^{-9} ~mathrm{C} }
$$

$$
C)~ q_2 = 3 cdot 10^{-9} ~mathrm{C}
$$

In this problem we must find the net force acting on the positive charge placed between two positive charges. Magnitude of positive charge in between two other charges is
$q_B = 3.1 cdot 10^{-6} ~mathrm{ C}$.
First positive charge is $q_A = 8.5 cdot 10^{-6} ~mathrm{ C}$ and it is placed at a distance $r_A = 4.2 ~mathrm{cm} = 0.042 ~mathrm{m}$ to the left from charge $q_B$.
Second positive charge is $q_C = 6.4 cdot 10^{-6} ~mathrm{ C}$ and it is placed at a distance $r_C = 2.9 ~mathrm{cm} = 0.029 ~mathrm{m}$ to the right from charge $q_B$.
What happens in this problem is that positive charge $q_B$ will be repelled by both of the other charges and thus it will be pushed in the direction of both of the charges. However, since it can’t move to both of the charges, resulting force $F$ is what’s going to decide the direction of overall repulsion between positive charge and the other two charges.
Since we have two forces acting in the opposite direction, magnitude of the resulting force $F$ will be calculated as:

$$
begin{equation}
| F| = |F_C| – |F_A|
end{equation}
$$

where $F_A$ is magnitude of the repulsive force between charge $q_B$ and charge $q_A$, whereas $F_C$ is repulsive force between charge $q_C$ and charge $q_B$. We know that the electric force $F$ between charges $q_A$ and $q_B$ at a distance $r$ from each other is given as:

$$
begin{equation}
F_{AB} = dfrac{k q_A q_B}{r^2}
end{equation}
$$

where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.

We are given distance $r_A$ between the first positive charge $q_A$ and charge $q_B$ and we are also given $q_B$ and $q_A$, which means that we can calculate the magnitude of the force $F_A$ between these two charges as:

$$
F_A = dfrac{k q_A q_B}{r_A^2}
$$

We are given distance $r_C$ between the second positive charge $q_B$ and positive charge $q_C$ and we are also given $q_C$ and $q_B$, which means that we can calculate the magnitude of the force $F_C$ between these two charges as:

$$
F_C = dfrac{k q_B q_C}{r_C^2}
$$

Now that we have the equations for magnitude of forces $F_A$ and $F_C$, we can calculate the magnitude of the resulting force by plugging in the expressions for $F_A$ and $F_C$ into equation $(1)$:

$$
begin{align*}
F &= dfrac{k q_C q_B}{r_C^2} – dfrac{k q_A q_B}{r_A^2} \
F &= kq_B bigg( dfrac{ q_C }{r_C^2} – dfrac{ q_A }{r_A^2} bigg) \
%
%
F &= 3.1 cdot 10^{-6} ~mathrm{ C} cdot 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}
bigg( dfrac{ 6.4 cdot 10^{-6} ~mathrm{ C}}{( 0.029 ~mathrm{m} )^2 } – dfrac{ 8.5 cdot 10^{-6} ~mathrm{ C} }{ 0.042 ~mathrm{m} )^2 } bigg) \
%
%
F &= 27.9 cdot 10^{-3} ~mathrm{N} cdot bigg( dfrac{ 6.4 }{( 0.029 ~mathrm{m} )^2} – dfrac{ 8.5 }{ ( 0.042 ~mathrm{m} )^2 } bigg) \
F &= |F_C| – |F_A| = 77.8799 ~mathrm{N}
end{align*}
$$

Notice that since we assumed magnitude of the force to be calculated as $F = F_C – F_A$ and we calculated a positive value of $F$, this means magnitude of the repulsive force $F_C$ is higher than magnitude of repulsive force $F_A$, which means that direction of force $F$ is in the direction from positive charge $q_B$ to charge $q_A$, to the left.

$$
boxed{ F = 78 ~mathrm{N}, text{toward A}}
$$

$$
A)~ F = 78 ~mathrm{N}, text{toward A}
$$

We are told that there are
$N = 4.8 cdot 10^{10}$
excess electrons on an electroscope and we must find charge $q$ on an electroscope.
We know that total charge $q$ on any object must be equal to a product of a whole number $N$ and elementary charge $e = 1.6 cdot 10^{-19} ~mathrm{C}$. This is due to a fact that elementary charge is the least amount of charge on any object and any other charge on an object is equal to:

$$
q = N e
$$

Since there are excess electrons on electroscope, charge on electroscope is negative, but we only need to calculate the magnitude of charge.
Let’s now use the equation above to calculate charge $q$ on electroscope:

$$
begin{align*}
q &= N e \
q &= 4.8 cdot 10^{10} cdot 1.6 cdot 10^{-19} ~mathrm{C} \
q &= 7.68 cdot 10^{-9} ~mathrm{C}
end{align*}
$$

$$
boxed{ q = 7.7 cdot 10^{-9} ~mathrm{C} }
$$

$$
C)~ q= 7.7 cdot 10^{-9} ~mathrm{C}
$$

Coulomb’s law states that the electric force $F$ between charges $q_A$ and $q_B$ at a distance $r_i$ from each other is given as:

$$
F = dfrac{k q_A q_B}{r_i^2}
$$

where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.

At first, charges $q_A$ and $q_B$ are at an initial distance between $r_i$, which makes the initial force $F_i$ between them equal to:

$$
F_i = dfrac{k q_A q_B}{r_i^2}
$$

In the final case, charges $q_A$ and $q_B$ at a 6 times greater distance $r_f = 6 r_i$ from each other and force $F_f$ in this final case is given as:

$$
F_f = dfrac{k q_A q_B}{r_f^2}
$$

To calculate force $F_f$ in the final case, we’ll divide the equation for $F_f$ and equation for $F_i$:

$$
begin{align*}
dfrac{F_f}{F_i} &= dfrac{ dfrac{k q_A q_B}{r_f^2} }{ dfrac{k q_A q_B}{r_i^2} } \
dfrac{F_f}{F_i} &= dfrac{ r_i^2 }{ r_f^2 } \
text{$r_f = 6 r_i$} \
dfrac{F_f}{F_i} &= dfrac{ r_i^2 }{ (6 r_i )^2 } \
dfrac{F_f}{F_i} &= dfrac{ 1 }{ 36 } \
F_f &= dfrac{F_i}{36} \
F_f &= dfrac{86~mathrm{N}}{36}\
F_f &= 2.3889 ~mathrm{N}
end{align*}
$$

$$
boxed{F_f = 2.4 ~mathrm{N}}
$$

Note that we could expect that force will be 36 times less when distance between the same two charges is 6 times greater because force is inversely proportional to the square of the distance between the charges.

$$
A)~ F_f = 2.4 ~mathrm{N}
$$

Coulomb’s law states that the electric force $F$ between charges $q_A$ and $q_B$ at a distance $r$ from each other is given as:

$$
F = dfrac{k q_A q_B}{r^2}
$$

where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.

At first, we had two bodies with same charge $q_A = q_B = q$ at a distance $r$,
which means that the initial force $F_i = 90 ~mathrm{N}$ between them is calculated as:

$$
F_i = dfrac{k q q }{r^2}
$$

In the final case, distance $r$ between the charges is the same, but charge on one of the bodies is tripled $q_A = 3q$, while charge on the other object remained the same $q_B = q$. Force $F_f$ in this final case is given as:

$$
F_f = dfrac{k q cdot 3q }{r ^2}
$$

To calculate the force in the final case, we’ll divide the equation for final force $F_f$ and initial force $F_i$:

$$
begin{align*}
dfrac{F_f}{F_i} &= dfrac{ dfrac{k q cdot 3q }{r ^2} }{dfrac{k q q }{r^2}} \
dfrac{F_f}{F_i} &= 3 \
F_f &= 3 cdot F_i \
F_f &= 3 cdot 90 ~mathrm{N} \
F_F &= 270 ~mathrm{N}
end{align*}
$$

$$
boxed{F_f = 2.7 cdot 10^2 ~mathrm{N} }
$$

$$
C)~ F_f = 2.7 cdot 10^2 ~mathrm{N}
$$

Newton’s law of universal gravitation states that the force $F_g$ between two objects with mass $m_A$ and $m_B$, that are at a distance $r$ between each other, is equal to:

$$
F_g = G dfrac{m_A m_B}{r^2}
$$

where $G = 6.67 cdot 10^{-11} ~mathrm{dfrac{Nm^2}{kg^2}}$ is gravitational constant.
This means that gravitational force between two alpha particles, each with $m_{alpha} = 6.68 cdot 10^{-27} ~mathrm{kg}$ is equal to:

$$
begin{equation}
F_g = G dfrac{m_{alpha} m_{alpha} }{r^2}
end{equation}
$$

where $r$ is distance between alpha particles.

Coulomb’s law states that the electric force $F_{e}$ between charges $q_A$ and $q_B$ at a distance $r$ from each other is given as:

$$
F_{e} = dfrac{k q_A q_B}{r^2}
$$

where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.
This means that electric force between between two alpha particles, each with charge $q_{alpha} = 3.2 cdot 10^{-19} ~mathrm{C}$ is equal to:

$$
begin{equation}
F_{e} = k dfrac{q _{alpha} q _{alpha}}{r^2}
end{equation}
$$

where $r$ is distance between alpha particles.

To find the ratio between the electric and gravitational force between two alpha particles, we’ll divide equations $(2)$ and $(1)$:

$$
begin{align*}
dfrac{ F_{e} }{ F_g} &= dfrac{ dfrac{k q _{alpha} q _{alpha} }{r^2} }{ G dfrac{m _{alpha} m _{alpha}}{r^2} } \
dfrac{ F_{e} }{ F_g} &= dfrac{ k q _{alpha} q _{alpha} }{ G m _{alpha} m _{alpha} } \
%
%
dfrac{ F_{e} }{ F_g} &= dfrac{ k q _{alpha}^2 }{ G m _{alpha}^2} \
%
%
&text{mass of alpha particle is $m _{alpha} = 6.68 cdot 10^{-27} ~mathrm{kg} $ } \
&text{mass of alpha particle is $q_{alpha} = 3.2 cdot 10^{-19} ~mathrm{C} $ } \
%
%
dfrac{ F_{e} }{ F_g} &= dfrac{ 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} cdot (3.2 cdot 10^{-19} ~mathrm{C})^2 } { 6.67 cdot 10^{-11} ~mathrm{dfrac{Nm^2}{kg^2}} cdot ( 6.68 cdot 10^{-27} ~mathrm{kg} )^2 } \
%
%
dfrac{ F_{e} }{ F_g} &= dfrac{ 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} cdot 10.24 cdot 10^{-38} ~mathrm{C^2} } { 6.67 cdot 10^{-11} ~mathrm{dfrac{Nm^2}{kg^2}} cdot 44.6224 cdot 10^{-54} ~mathrm{kg^2} } \
dfrac{ F_{e} }{ F_g} &=3.0965 cdot 10^{35}
end{align*}
$$

$$
boxed{ dfrac{ F_{e} }{ F_g} =3.1 cdot 10^{35}}
$$

$$
D)~ dfrac{ F_{e} }{ F_g} =3.1 cdot 10^{35}
$$

Coulomb’s law states that the electric force $F$ between charges $q_A$ and $q_B$ at a distance $r$ from each other is given as:

$$
F = dfrac{k q_A q_B}{r^2}
$$

where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.

We are told that charge on the balloon $q_1 = -8.9 cdot 10^{-14} ~mathrm{C}$ and charge on the sphere is $q_2 = 25 ~mathrm{C}$. This sphere and balloon are at a distance of $r = 2 ~mathrm{km} = 2 cdot 10^3 ~mathrm{m}$, which means that force between these two objects is calculated as:

$$
begin{align*}
F &= dfrac{k q_1 q_2 }{r^2} \
F &= dfrac{ 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} cdot (-8.9) cdot 10^{-14} ~mathrm{C} cdot 25 ~mathrm{C} }{(2 cdot 10^3 ~mathrm{m})^2} \
F &= dfrac{ 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} cdot (-8.9) cdot 10^{-14} ~mathrm{C} cdot 25 ~mathrm{C} }{4 cdot 10^6 ~mathrm{m^2}} \
F &= – 5 cdot 10^{-9} ~mathrm{N}
end{align*}
$$

Note that the minus sign in the result above means that the force between the balloon and charged sphere is attractive. Magnitude of this force is equal to:

$$
boxed{F =5 cdot 10^{-9} ~mathrm{N} }
$$

$$
B)~ F= 5 cdot 10^{-9} ~mathrm{N}
$$

Charges $q_A=-2.0 mathrm{~mu C}$, $q_B=-2.0 mathrm{~mu C}$ and $q_C=-4.0 mathrm{~mu C}$ are placed as shown on the diagram above.
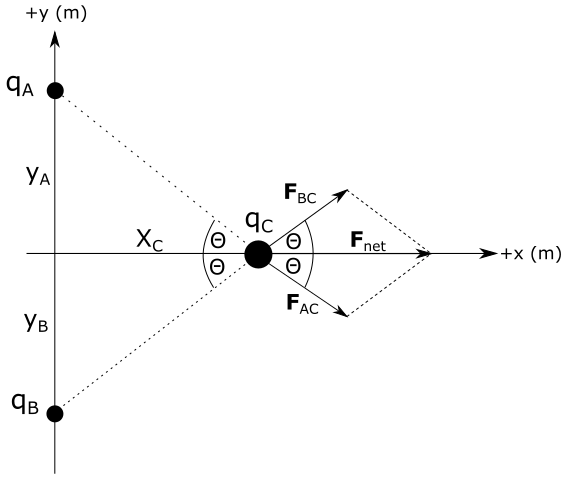
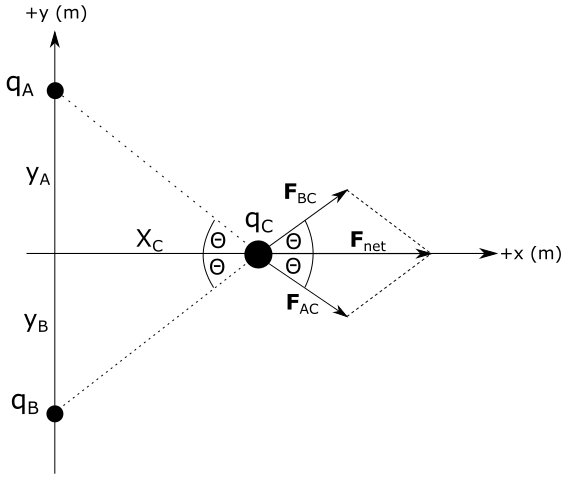
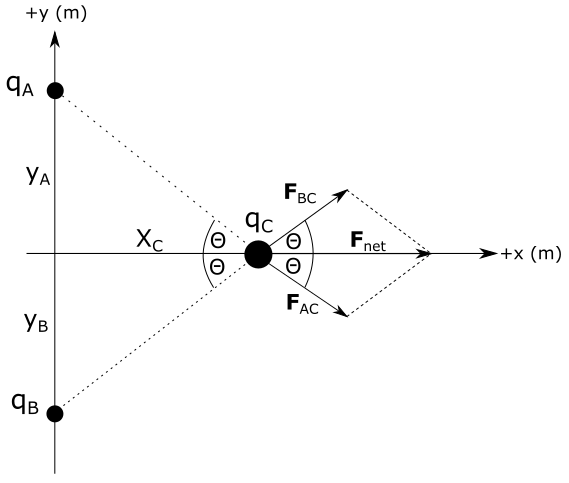
Distance of charge $q_A$ from the origin $y_A$ is equal to the distance of charge $q_B$ from origin $y_B = y_A=0.30 mathrm{~m}$. Distance of charge $q_C$ from the origin is $x_C=0.40 mathrm{~m}$ along horizontal axis.

Direction of the force vectors $F_{AC}, F_{BC} and F_{net}$ is shown on the diagram above. Since all charges have the same sign, forces between them are repulsive. We will now calculate magnitudes of these vectors.
Coulomb’s law states that the magnitude of the electric force $F_e$ acting between charges $q_1$ and $q_2$, at a distance $r$ from each other is given as:

$$
F_e = dfrac{k q_1 q_2}{r^2}
$$

where $k = 8.99cdot 10^9 mathrm{ ~ dfrac{Nm^2}{C^2} }$ is Coulomb’s constant.

From Coulomb’s law it follows that magnitude of the vector of force $F_{AC}$, acting between charges $q_A$ and $q_C$ is equal to:

$$
F_{AC} =k cdot dfrac{q_Acdot q_C}{(r_{AC})^{2}}\
$$

where $r_{AC}$ is distance between charges $q_A$ and $q_C$ that can be calculated from Pythagorean theorem as:

$$
r_{AC}^{2}=y_A^2+x_C^2
$$

We’ll plug in this expression for $r_{AC}$ to calculate $F_{AC}$:

$$
begin{align*}
F_{AC}&=k cdot dfrac{q_Acdot q_C}{(y_A^2+x_C^2)}\
tag{ plug in the values }\
F_{AC}&=8.99cdot 10^9 mathrm{ ~ dfrac{Nm^2}{C^2} } cdot dfrac{2.0 mathrm{~mu C}cdot 4.0 mathrm{~mu C}}{(0.30 mathrm{~m})^2+(0.40 mathrm{~m})^2}\
tag{ $ 2.0 ~mathrm{mu C} = 2 cdot 10^{-6 } ~mathrm{C} $ } \
tag{ $ 4.0 ~mathrm{mu C} = 4 cdot 10^{-6 } ~mathrm{C} $ } \
F_{AC}&=8.99cdot 10^9 mathrm{ ~ dfrac{Nm^2}{C^2} } cdot dfrac{2.0 cdot 10^{-6}mathrm{~ C}cdot 4.0 cdot 10^{-6} mathrm{~C}}{(0.30 mathrm{~m})^2+(0.40 mathrm{~m})^2}\
F_{AC}&=8.99cdot 10^9 mathrm{ ~ dfrac{Nm^2}{C^2} } cdot dfrac{8.0 cdot 10^{-12}mathrm{~ C}}{0.09 mathrm{~m^2}+0.16 mathrm{~m^2}}\
F_{AC}&=8.99cdot 10^9 mathrm{ ~ dfrac{Nm^2}{C^2} } cdot dfrac{8.0 cdot 10^{-12}mathrm{~ C}}{0.25 mathrm{~m^2}}
end{align*}
$$

$$
boxed{F_{AC} =287.68 cdot 10^{-3} mathrm{~N}}
$$

From the diagram above we can easily see that magnitude of the vector of $F_{BC}$ acting between charges $q_B$ and $q_C$
is equal to magnitude of vector $F_{AC}$.

$$
boxed{F_{BC} =287.68 cdot 10^{-3} mathrm{~N}}
$$

This is due to a fact that, following the Coulomb’s law, force between the two charges depends on their distance $r$ and magnitude of both of the charges and since $q_A = q_B$ and $r_{AC} = r_{BC}$, we conclude that

$$
F_{BC} = F_{AC}
$$

Thus:

$$
boxed{ F_{BC} =287.68 cdot 10^{-3} mathrm{~N}}
$$

We need to determine magnitude of the net force $F_{net}$ acting on charge $q_C$.
Vector $vec{F}_{net}$ is equal to a vector sum of vectors $vec{F}_{AC}$ and $vec{F}_{BC}$:

$$
begin{align*}
vec{F}_{net}=vec{F}_{AC}+vec{F}_{BC}
end{align*}
$$

By taking square of both sides:

$$
begin{align*}
F_{net}^{2}&=F_{AC}^{2}+F_{BC}^{2}+2cdot vec{F}_{AC} cdot vec{F}_{BC}
end{align*}
$$

Dot product term $vec{F}_{AC} cdot vec{F}_{BC}$ appears on the right side of the equation above. Dot product of two vectors is equal to a product of magnitudes of those vectors and cosine of angle between them. From the diagram we see that angle between vectors $vec{F}_{AC}$ is $2 theta$. By plugging this into last equation we have:

$$
begin{align*}
F_{net}^{2}&=F_{AC}^{2}+F_{BC}^{2}+2cdot F_{AC} cdot F_{BC} cdot cos 2 theta\
end{align*}
$$

By taking square root of both sides, we obtain expression for magnitude of net force vector $F_{net}$:

$$
begin{align*}
F_{net}&=sqrt{F_{AC}^{2}+F_{BC}^{2}+2cdot F_{AC} cdot F_{BC} cdot cos 2 theta}
end{align*}
$$

$$
F_{net} =sqrt{F_{AC}^{2}+F_{BC}^{2}+2cdot F_{AC} cdot F_{BC} cdot cos 2 theta}
$$

The only unknown value on right side of the equation above is angle $theta$.
We can find this angle from the right triangle on the left from charge $q_C$. We can see from the figure above that distances $x_C$, $y_A$ and $r_{CA}$ form a right triangle, from which it follows:

$$
begin{align*}
tan theta &= dfrac{y_A}{x_C}\
tag{take $arctan$ of the equation above} \
theta &= arctan dfrac{y_A}{x_C}\
tag{plug in the values} \
theta &= arctan dfrac{0.30 mathrm{~m}}{0.40 mathrm{~m}}\
theta &= 36.86^{circ}
end{align*}
$$

By plugging in the value for angle $theta$ into the equation for $F_{net}$, we can finally calculate $F_{net}$:

$$
begin{align*}
F_{net}&=sqrt{(0.28768 mathrm{~N})^{2}+(0.28768 mathrm{~N})^{2}+2cdot (0.28768 mathrm{~N})^2 cdot cos (2 cdot 36.86^{circ})}\
F_{net}&=sqrt{0.0827 mathrm{~N^2}+0.0827 mathrm{~N^2}+2cdot 0.28768 mathrm{~N} cdot 0.28768 mathrm{~N} cdot cos (73.72^{circ})}\
F_{net}&=sqrt{0.0827 mathrm{~N^2}+0.0827 mathrm{~N^2}+2cdot 0.28768 cdot 0.28768 cdot cos (73.72^{circ}) mathrm{~N^2}}\
F_{net}&=sqrt{0.0827 mathrm{~N^2}+0.0827 mathrm{~N^2}+2cdot 0.28768 cdot 0.28768 cdot 0.28 mathrm{~N^2}}\
F_{net}&=sqrt{0.0827 mathrm{~N^2}+0.0827 mathrm{~N^2}+0.046 mathrm{~N^2}}
end{align*}
$$

$$
boxed{F_{net} =459.78 cdot 10^{-3} mathrm{~N}}
$$

$$
begin{align*}
& F_{AC} =287.68 cdot 10^{-3} mathrm{~N} \
& F_{BC} =287.68 cdot 10^{-3} mathrm{~N} \
& F_{net} =459.78 cdot 10^{-3} mathrm{~N} \
end{align*}
$$